基于Transformer的短期血糖预测方法研究

王译文,黎建军,曲再鹏

(中国计量大学 机电工程学院,浙江 杭州 310018)

糖尿病是一种由于胰腺分泌胰岛素不足或者不能分泌导致的慢性疾病[1]。国际糖尿病联盟(IDF)官网最新发布的第10版全球糖尿病地图报告显示,糖尿病导致了全球超过1/10的死亡,截止到2021年,全球5.37亿20～79岁成人患有糖尿病,约占全世界该年龄段总数的1/10,预计到2045年糖尿病患者数量将增长到7.83亿,其中中国是全球糖尿病成人患者数量最多的国家[2]。胰岛素泵,又称人工胰脏,是目前最有望成为糖尿病患者血糖科学管理与治疗的设备。连续血糖监测设备(CGMS)是人工胰脏的重要组成部分,它为胰岛素泵提供实时的血糖信息,胰岛素泵控制器根据血糖数据信息调节胰岛素输注量使患者身体维持健康的血糖水平[3]。由于糖尿病患者的血糖变化是一个复杂的非线性过程,同时胰岛素作用于人体具有时滞性,实现低血糖暂停是确保糖尿病患者安全的前提,预测性血糖监测系统这一功能通过算法预测血糖水平下降到阈值以下,能够提前暂停或调节胰岛素输注[4]。

血糖预测模型分为知识驱动模型、数据驱动模型和混合模型三大类,知识驱动模型需要构建人体血糖生理模型,其参数通常不精确,实现过程特别复杂[5]。随着血糖传感技术的不断发展,近年来基于数据驱动的血糖预测模型逐渐增加,数据驱动模型主要基于CGM采集的血糖测量序列,还有一些方法将输入(葡萄糖、膳食、胰岛素、运动等)结合起来,Zecchin等[6]采用了15名T1D受试者的数据,通过基于神经网络算法添加不同输入进行对比实验,用平均绝对误差以及时间增益来评估预测效果,结果表明,胰岛素输入以及摄入碳水化合物相关的输入并不会改善30 min内的短期预测效果。从糖尿病患者的实际血糖管理角度出发,多输入数据的采样与统计复杂程度较大,可应用性不高,因此尽可能选取方便采集的数据作为输入特征,Hamdi等[7]采用了差分进化(DE)算法加权的支持向量回归(SVR)方法预测短期血糖,选取了12例糖尿病患者的真实CGM数据进行了验证,取得了较高的预测精度。Li等[8]提出了一种基于漏积分神经元和岭回归学习算法优化的回声状态网络结构,比极限学习机(ELM)和反向传播(BP)算法具有更佳的预测效果。在时序预测领域循环神经网络(RNN)一直比传统预测方法具有独特的优势,RNN的变体长短记忆单元(long-short term memory,LSTM)以及门控循环网络(gated recurrent unit,GRU)近年来已在时序预测各领域表现出较好的预测效果[9],Sun等[10]采用了一个具有一个LSTM层、一个双向LSTM层和几个完全连接层的序列模型在预测血糖浓度,基于评估标准,LSTM网络优于线性平均移动差分(ARIMA)和SVR。滕建丽等[11]采用一种基于GRU血糖预测模型,比基本RNN网络、LSTM、支持向量回归具有更好的预测精度。由于RNN方法在面对长序列预测时无法完全消除梯度消失和梯度爆炸等问题,而Transformer模型能够解决该问题,同时可以捕获长期相关性[12],因此Transformer模型在时序预测方面得到了广泛关注,近年来开始逐步研究并应用于各领域[13-15]。

本文旨在将Transformer模型应用于血糖预测领域。首先在预测效果优异性方面,与其他模型进行对比分析;同时,在预测性能分析方面,探究不同输入长度对模型预测精度的影响;最后,在预测长度有效性方面,通过克拉克网格误差分析Transformer模型的临床适用性。

1 Transformer模型原理

Transformer模型是一个序列到序列的模型,它由输入层、解码层、译码层和输出层四部分组成,如图1。不像传统的RNN顺序结构,它是一种基于Self-Attention机制的架构,具有更好的并行运算能力以及可解释性。因此,Transformer模型在一些特定时间序列预测场景应用中具有一定的适用性。

图1 Transformer模型原理框架Figure 1 Transformer model principle framework

输入层主要由嵌入层与位置编码层组成,嵌入层主要用于序列数据的向量输入,经过输入Embedding层得到嵌入向量:Xu={x1,x2,…,xT},Xu∈RT×dModel,其中T为输入序列的长度,dModel为嵌入层的维度,x1～xT为输入序列中第1～T位置的嵌入向量。

位置编码层是为了确定序列的位置信息,由于没有RNN与CNN中的递归层和卷积层,仅仅依靠自注意力机制无法获取输入的顺序信息,需要主动将序列的顺序信息传递给模型,Transformer采用正弦和余弦函数对序列Xu进行位置编码来得到相对位置和绝对位置,其公式为

PE(t,2i)=sin(t/10 0002i/dModel),

(1)

PE(t,2i+1)=cos(t/10 0002i/dModel)。

(2)

式(1)(2)中,t表示当前序列位置,i表示维度,2i表示偶数位置,2i+1表示奇数位置,dModel表示输入特征的维度,PE表示由奇数列和偶数列所得到的位置编码结果。将位置编码信息加入到嵌入层得到向量Gu表示为

Gu=Xu+PE。

(3)

编码层是由多头注意力层、前馈全连接层和两个残差连接和归一化层组成。

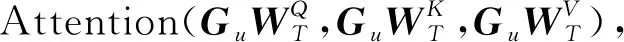
(4)

(5)

前馈全连接层是由两个线性变换组成,中间有一个ReLu激活函数,由于仅仅依赖多头注意力机制不能够达到理想情况,通过该层可以提升网络的性能,其数学表达式如下:

FFN(x)=max(0,xW1+b1)W2+b2。

(6)

式(6)中:W1和W2为权值矩阵;b1和b2为偏置项,x为输入。

残差连接和归一化层的作用主要是提高信息传递深度,防止梯度消失,加快模型的收敛能力。

(2)对比可焊性可知，R1，R6，R10，W1以及PDC的可焊性大致排序：R6>R1>R10>PDC>W1。

译码层中间的结构与编码器相似,但是译码层中的注意力层与编码器的有所不同,译码器是自回归的,在序列预测中考虑未来位置的信息会对当前位置的信息造成干扰,为了防止未来信息可能被提前利用,因此将未来信息用函数掩码掉,本文的预测模型中将译码层用线性层替换。

输出层主要由一个线性变换层和一个Softmax层构成,其中线性变换层是一个简单的全连接神经网络层,它可以将译码器输出的向量结果转换到指定的维度,最后通过Sigmoid压缩函数和反归一化处理得到对应的输入序列的预测值Y={y1,y2…yT}。

2 实验对比和分析

2.1 数据集来源

本文数据来源于美国国立卫生研究院发布的DirectNet糖尿病临床数据集,该数据集记录着有100多名糖尿病儿童患者的连续血糖数值,数据采样时间间隔为5 min,由专业的连续血糖监测系统所得。图2为某糖尿病患者连续3 d监测的血糖变化曲线。

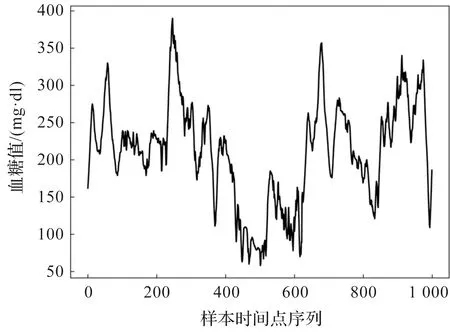
图2 某糖尿病患者连续3 d血糖变化曲线Figure 2 Blood glucose curve of a diabetic patient for 3 consecutive days

2.2 模型评估

均方根误差和平均百分比误差被广泛当作量化血糖预测模型性能的两个评估指标。均方根误差和平均百分比误差的计算公式如下:

(7)

(8)

本文使用血糖历史值作为模型输入序列,为了探究Transformer与其他模型的预测性能,分别使用LSTM、GRU和Transformer的方法进行血糖预测。以RMSE和MAPE作为上述模型血糖预测精度的评估指标,选用5 min的输入序列时长为例,分别采用数据集的前70%作为训练集,后30%作为测试集。为避免血糖预测的偶然性,对5名糖尿病患者进行不同预测时长(5 min、15 min、30 min、45 min、60 min)的RMSE以及MAPE的结果对比,如表1和表2。

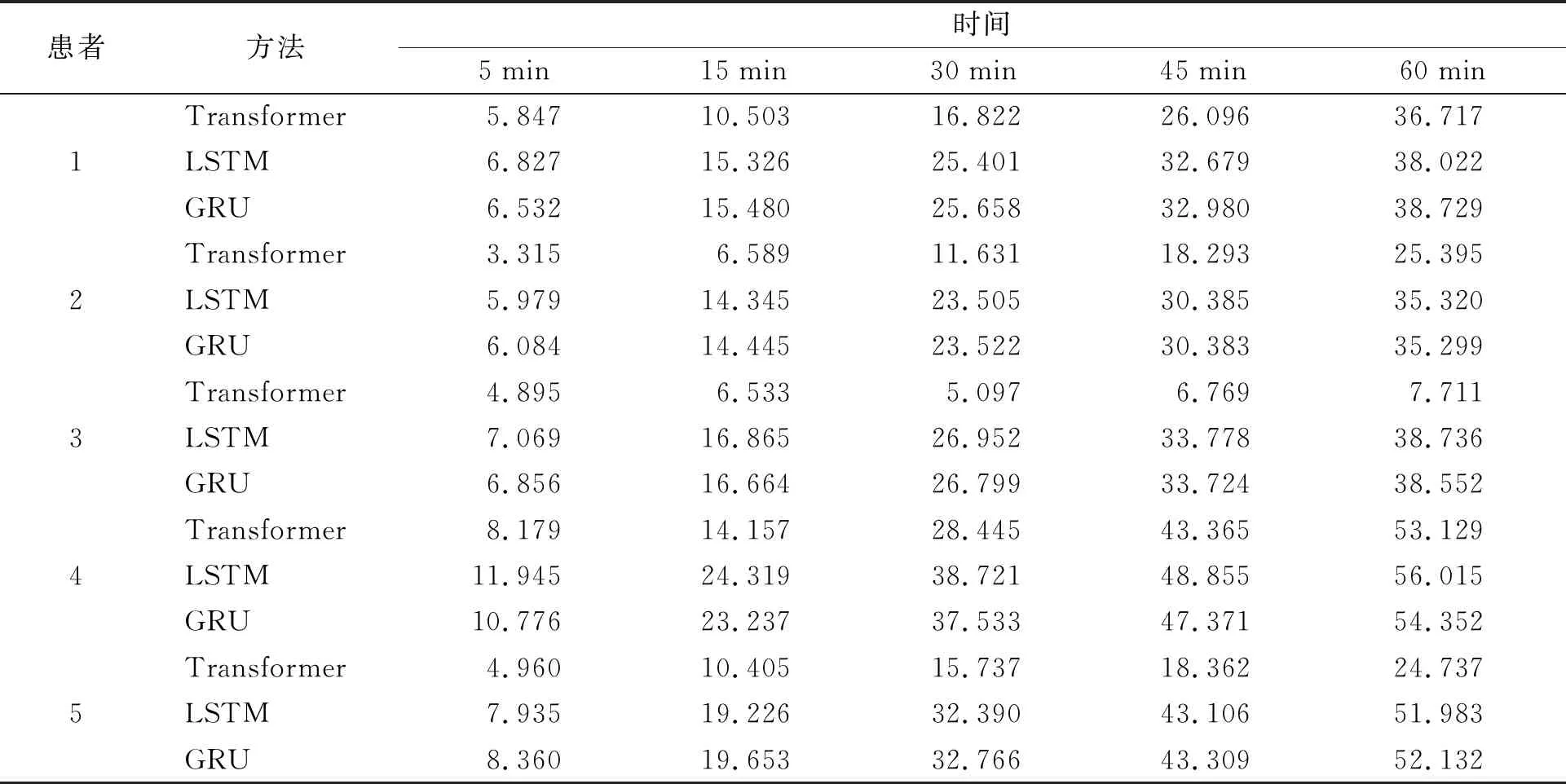
表1 5名糖尿病患者的RMSE

表2 5名糖尿病患者的MAPE

分析表1与表2中的数据可知,Transformer算法在不同预测时长内的预测效果均优于其他两种算法。另外,由于不同患者的血糖波动特性存在差异,在某些患者的短期血糖预测中,Transformer算法表现出了更小的预测偏差,且预测偏差不会随预测时长的增长而发生显著的变化。

2.3 不同输入序列长度下模型预测性能分析

血糖预测模型是根据历史血糖值来预测未来短期血糖值,所以模型输入的序列长度会影响模型预测性能。若将Transformer模型应用于人工胰脏的高、低血糖的预警系统中,利用先验知识充分反映出患者的未来趋势,则必须对历史血糖值输入序列长度做更深一步的研究分析。

不同输入序列长度下,本文采用平均百分比误差(MAPE)作为模型预测性能的衡量标准,以5～30 min输入序列长度下的历史血糖值作为模型输入,预测患者未来1h内的血糖水平,并通过MAPE值评估模型预测精度,结果如图3。

图3 不同预测时长序列下的效果对比图Figure 3 Comparison of effects under different prediction time series

由图3可知,当输入序列在5～30 min范围变化时,不同输入序列下的血糖预测是存在差异的,其中输入序列时长为20 min时的MAPE最低,表明此时预测效果最优。说明血糖预测依赖短期历史输入序列中的信息,以及增加一定的输入序列长度能够提高血糖预测效果。同时,不同输入序列下MAPE的数值差异表明,不同输入序列下的血糖水平对血糖预测精度具有重要影响作用。

2.4 克拉克误差网格分析

克拉克误差网格分析(Clarke error grid analysis,EGA)是一种用于评估血糖值量技术准确性的临床性方法[16]。EGA图分别根据血糖预测值在A、B、C、D、E共5个区域来表示不同程度的预测效果。为了表现出血糖预测的准确性,A、B、C、D、E这5个区域分别有以下定义:①A区域:表示在临床上具有准确性,预测值与实际值的偏离度不超过20%;②B区域:表示预测值与实际值的偏离度超过20%,但其误差在可接受范围内;③C区域:表示可能会引起血糖的无效矫正,导致高血糖和低血糖的发生;④D区域:表示预测值与实际值的偏差不在正常范围内,其预测值偏差较大,不具有参考价值;⑤E区域:表示错误处理。若预测点在A、B区域范围内,则表明预测值是较为准确并且是可被接受的。

取2.3节得到最优的20 min的输入序列时长进行分析,其不同预测时长的EGA图如图4所示,并作出EGA图中的A、B、C、D、E区域占比表见表3。由表3和图4可知,在血糖未来预测时长为5 min时,A区域的占比为100%,能够达到最佳的血糖预测效果;当血糖未来预测时长为10 min、15 min、20 min、25 min、30 min时,其A、B区域占比总和一直保持100%,在预测中依然有着较高的准确性,能够达到理想的血糖预测效果;

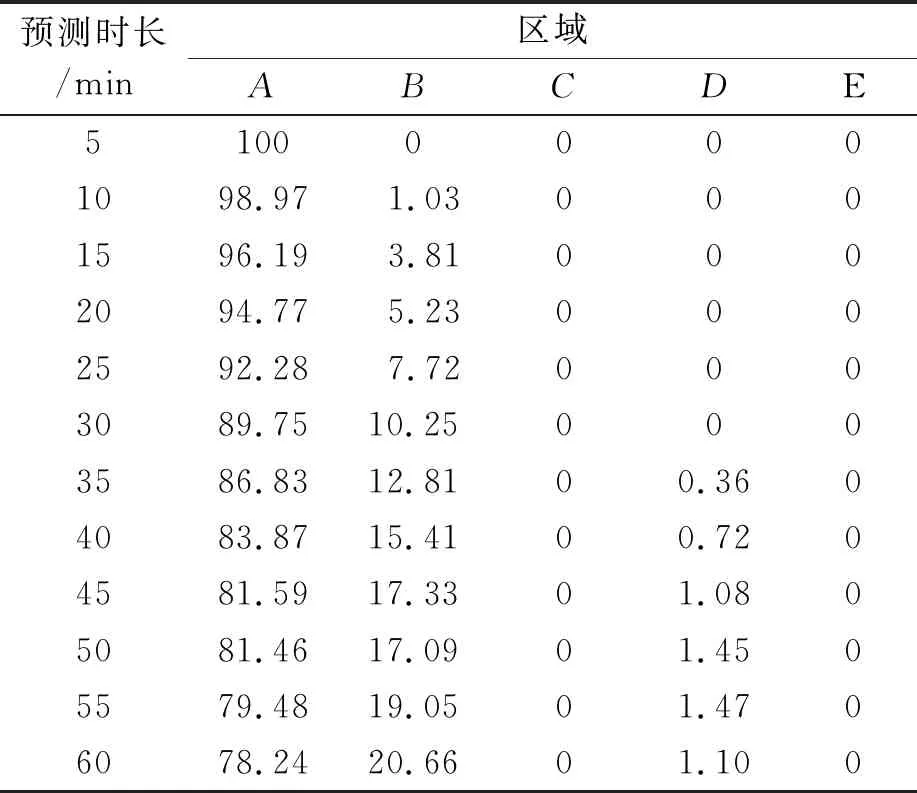
表3 不同预测时长下的EGA各区域占比

图4 5～60 min预测时长的EGA图(顺序从左往右)Figure 4 EGA chart of 5～60 min prediction duration ( from left to right )

当血糖预测时长在30～60 min内时,D区域的占比在较低的水平上保持上升,A、B区域的占比之和仍处在较高水平,能够实现良好的预测。以上分析表明,在无进餐、运动以及胰岛素输注的影响下,30 min内的血糖预测是能够达到较高的预测精度。

3 结 语

本文提出了基于Transformer的短期血糖预测模型,并与LSTM和GRU进行对比分析,以RMSE和MAPE作为血糖预测性能的评估指标,结果表明,相较于LSTM和GRU预测模型,Transformer模型在血糖预测中具有更加优异的表现。另外,对于不同输入序列长度下的Transformer模型进行对比讨论,由MAPE评估指标分析结果表明,输入序列时长为20 min的预测效果最优。最后,进一步对未来不同预测时长内的预测效果进行探究,采用克拉克网格误差分析图表现其预测性能,结果表明,Transformer血糖预测模型是一种较好的短期血糖预测方法。