氨基酸带电量及分布对蛋白质单链自组装行为的影响

俞志超,姜舟婷

(中国计量大学 理学院,浙江 杭州 310018)

蛋白质作为一种聚电解质,由多种不同的氨基酸构成,表现出不同的结构多样性。由于蛋白质的生物学功能在很大程度上取决于其独特的结构,该结构由残基之间复杂的相互作用决定。相互作用包括静电相互作用、亲疏水相互作用、范德华相互作用、吸附-电中和作用与吸附-架桥机理等[1-5],因此蛋白质链结构导致的多种机械和热力学性质,甚至生物功能,引起了科学家的广泛兴趣。聚合物链结构的形成,如聚合物结晶、蛋白质折叠、嵌段共聚物的自组装,最近已成为化学、物理、生物学和材料科学领域关注的焦点[6-9]。

根据安芬森的变性和复性实验已知,蛋白质的三维构象直接由其一级结构(氨基酸序列)决定[10]。带电氨基酸残基-残基接触过程中产生的静电相互作用在蛋白质结构转变过程中起着至关重要的作用,对蛋白质及其复合物的形成至关重要。2020年Dahal等[11]采用粗粒化分子动力学方法研究过氧化氢酶吸附带电表面的行为,实验发现蛋白质的吸附行为由表面和非均匀分布的蛋白质残基之间的局部静电相互作用决定,且随着表面吸附蛋白质的增加,其结构会因为蛋白质残基之间的静电排斥作用而改变。2020年Adesina等[12]通过使用腈探针(T46C-CN)插入大肠杆菌DHFR(EcDHFR)、其构象受损变体(EcDHFR-S148P)和嗜热脂肪土杆菌DHFR(BsDHFR)的二氢叶酸还原酶(DHFRs)反应中心附近,实验发现当辅因子与酶结合时,底物向探针投射的电场抵消了辅因子施加的电场,这表明控制具有静电性质的配体-配体相互作用可能是创造高效酶的关键因素。2016年Tsai等[13]在基于AWSEM模型模拟静电作用对13个单体蛋白质和4个二聚体结构的影响并对其进行结构预测。模拟结果表明,对于单体蛋白质,除非蛋白质具有特殊的带电氨基酸分布,如核糖体蛋白S6,否则静电相互作用的添加不会显著提高结构预测的质量。静电作用在二聚体的结合过程中发挥着更重要的作用,提供了电荷与电荷之间的稳定性,如蛋白质复合物KIX-pKID的结合在很大程度上由静电作用辅助。

基于原子水平的计算机模拟方法对蛋白质相互作用方式进行研究,已被越来越多的科学家所采纳。但是随着研究体系的不断增大,常规的全原子模型遇到了瓶颈,比如计算一个原子数为N的体系,其计算量为NlogN,随着体系原子数的增加,其动力学行为会更复杂,构象空间也会大大增加,这就要求分子动力学模拟要持续足够多的时间来保证体系构象空间的采样。为了解决上述问题,近些年来人们提出了粗粒化模型,即将较多的自由度整合到较少的自由度从而简化对体系的描述[14-15]。虽然粗粒化模型不能给出蛋白质折叠过程中所有的原子细节,但能在更长的时间尺度执行计算,这是了解整个相互作用过程的动力学行为和热力学特征并挖掘潜在物理机制的关键。

LAMMPS作为一款开源性软件,随着近些年各领域的研究者对其算法进行更新迭代,使其功能不断完善,如2018年Edorh等[16]基于多重网格算法对P3M模型进行更新,能够高效计算自适应约束系统中粒子的静电势。由于LAMMPS极易扩展的特点,研究者可根据自身需求构建模型,设置外界条件,对于粗粒化模型的分析十分方便,如2021年Ford等[17]对粘蛋白(MUC5B)进行粗粒化模拟,通过LAMMPS探索在1.5～5 mg/mL质量浓度下MUC5B结构域之间疏水和静电相互作用强度。实验发现,随着粘蛋白浓度的升高,其相互作用强度越大;粘蛋白浓度和化学相互作用强度都在粘液中发现的结构形态和流变性方面发挥作用。

利用计算机模拟各种势能场中的蛋白质结构和性质,可以在一些领域获得与实验相同的结果从而验证实验的准确性[18-19],也可以根据物理化学性质构造蛋白质链,研究其结构转变的影响因素,为蛋白质结构预测、蛋白质功能改造等方面提供理论支持。本文利用LAMMPS软件对蛋白质链进行粗粒化建模,利用分子动力学模拟由不同带电量及连续带电氨基酸的数目组成的蛋白质链的结构特征,分析二者对蛋白质体系的能量和结构并找出内在联系。

1 模型及计算方法

对于聚合物科学中的许多问题,详细描述聚合物的化学结构和参数会使模拟的主要特征淹没在无穷的细节之中,浪费有限的计算资源,但是模型过于简化又会使模拟结果无法反映体系的主要特征。我们采用非格点(珠链)模型,保留基本大分子的特征,如链分子的连接性、非键合相互作用,同时考虑氨基酸残基的属性,对蛋白质链进行构建[20-21],用简化的氨基酸残基组合来表示蛋白质的序列,从而简化蛋白质能量的计算。

本文所有的分子动力学模拟均采用全原子Dreiding力场[22]进行,构造的模型链由200个氨基酸构成,模拟盒子大小为20 nm×20 nm×20 nm,并采用周期性边界条件。模拟期间非键相互作用的截断半径为1 nm,模拟温度为300 K,模拟时间步长为2.5 fs,每隔5 ps输出一次坐标。

蛋白质体系能量由键能和非键能构成,其中键能包括键伸缩能、键角弯曲能、键扭转能,非键能包括静电能、范德华能。

本文通过改变蛋白质链上单个氨基酸的带电量q(0～1C)和带相同极性电荷氨基酸的连续数目M(5、10、20、25、50),来研究单链的行为。为了使模拟体系整体呈电中性,蛋白质单链上带有相反电荷的氨基酸数目相同,且正负极性的带电量之和相等。M为10的蛋白质链初始构型如图1,10个连续的红色珠子表示10个连续带正电的氨基酸,10个连续的蓝色珠子表示10个连续带负电的氨基酸。在总长为200的蛋白质链上,红色珠子与蓝色珠子数目相同,说明蛋白质链上氨基酸带电量之和为0,体系呈电中性。

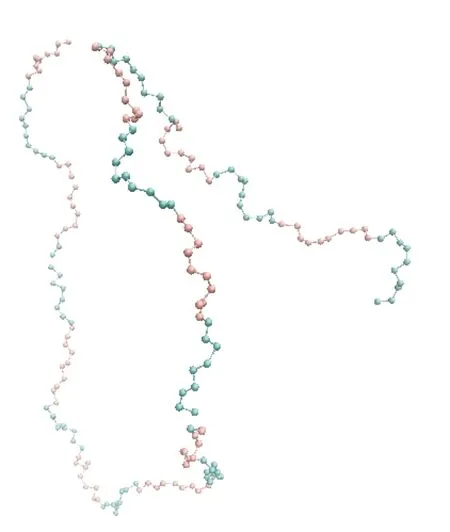
图1 带相同极性电荷氨基酸的连续数目M=10的蛋白质链初始构型图Figure 1 Initial configuration diagram of protein chains with continuous number M=10 of amino acids with the same polar charge

我们用一个珠子代表一个氨基酸,使用5个势函数来构建模型蛋白质链[23-24],其中键能包括键伸缩能、键弯曲能和键扭转能,非键能包括范德华能和静电能。它们的表达式如下。

1)相邻珠子的键伸缩能:

(1)

其中,l0为平衡键长,大小为0.153 nm,li为相邻珠子i-1和i之间的键长。键伸缩能常数kd=2.929×105kJ/(nm2·mol)。

2)每三个相邻珠子的键弯曲能:

(2)

其中,平衡键角θ0=1.231 rad和θi是3个相邻珠子i-2、i-1和i之间的键角。键弯曲势能常数kθ=418.4 kJ/(rad2·mol)。

3)每4个相邻珠子的键扭转能:

(3)

其中,φi是由4个连续的珠子i-3、i-2、i-1和i沿着主线组成的两个平面的二面角。键扭转能常数kφ=8.368 kJ/mol。

4)范德华能通过截断的12-6LJ势作用于所有两个以上键的珠子组合:

(4)

其中rij是珠子i和珠子j间的距离。范德华相互作用参数值分别为ε=0.830 1 kJ/mol,σ=0.362 4 nm。

5)两个带电珠子的静电能:

(5)

其中rij是珠子i和珠子j之间的距离。C是一个能量转换常数,ε是介电常数,qi和qj是这两个珠子上的电荷,在本文中作为模拟体系的变量。

蛋白质的结构特征是我们讨论的重点,主要根据体系的回转半径(Rg)和其可视化结构图分析蛋白质链随氨基酸带电荷情况的变化趋势。

结构参量回转半径(radius of gyration,Rg)描述蛋白质分子的整体尺寸,标志着蛋白质分子的疏松程度。回转半径值越大说明体系越松散。回转半径Rg的定义为

(6)

其中N是体系中蛋白质原子的数量,r(i)和rcenter分别是第i原子的坐标和质心的坐标。

2 结果与讨论

2.1 能量分析

图2给出了蛋白质链的范德华能(a)、静电能(b)、键能(c)和总势能(d)随连续带同极性电荷的氨基酸数目M的变化趋势,其中键能是键伸缩能、键弯曲能和键扭转能之和。在图2(a)中,当单个氨基酸带电量q小于等于0.2C时,体系的范德华能处于负值,其随M的增加变化并不明显,范德华能随着氨基酸带电量的影响也较小;当q大于0.2C时,范德华能为正,并随M的增加而

图2 由带电量为q的氨基酸组成的蛋白质链的不同能量随连续相同电荷氨基酸数目M的变化趋势图Figure 2 Different energy of the protein constructed by the residues with charge q and the number of sequentially changed residues M

上升的趋势变得显著,尤其当M值小于25时更为明显,同时,范德华能随单个氨基酸带电量的增加而增加,即上升趋势与单个氨基酸带电量q的大小呈正相关。当蛋白质链上带相同极性电荷氨基酸的连续数目M大于25时,体系范德华能变化趋势逐渐缓慢。图2(b)中,静电能随单个氨基酸的带电量q及连续相同电荷氨基酸数目M的变化情况,与范德华能的趋势都相反,即体系的静电势能随M的增加而呈下降趋势,并且这种趋势在相同极性电荷氨基酸的连续数目M小于25时,变化明显。但当蛋白质链上M值大于25时,体系静电势能变化趋势逐渐缓慢,同时,静电能随单个氨基酸带电量的增加而减少,带电量越大,变化越显著。在图2(c)给出了蛋白质链体系的总的键能,其变化趋势和图2(a)相同,但是从能量变化范围来看,图2(a)在1 600 kJ/mol,而图2(c)的键能变化范围仅为图2(a)的1/4左右。说明体系键能与一级结构的氨基酸总数密切相关,但是受氨基酸的种类和分布的影响较小,而范德华能与氨基酸空间分布有关。当然,受参数影响最大的是静电能,体系静电势能的绝对值要远远大于键能和范德华能,因此,蛋白质体系的总能量的变化趋势图2(d)与图2(b)即静电能随M和q值的变化趋势一致,即体系主要受静电相互作用的影响。

2.2 结构分析

本文研究了在单个氨基酸带电荷相同的情况下连续带电荷的氨基酸数目对蛋白质链结构的影响,通过研究蛋白质链的回转半径判断蛋白质链结构的松散程度,如图3。图3(a)中可以看出,在单个氨基酸带电量q为0.05C的情况下,链的回转半径大小在0.792～0.945 nm范围内,且无论M值为多大,其回转半径波动范围均在0.05 nm左右。图中M为50的情况下,回转半径曲线稳定在0.8 nm左右,其余情况下的回转半径曲线稳定在0.85 nm左右。这说明当链上连续带同极性电荷氨基酸数目越多时,蛋白质链结构越紧密。图3(b)中可以看出,在单个氨基酸带电量q为0.4C的情况下,M为5、10的回转半径相较于q为0.05C的情况均有不同幅度的上升,而M为20、25和50的回转半径却有下降,且曲线的波动幅度从0.05 nm降至0.02 nm,这说明单个氨基酸带电量增大时,蛋白质链上受静电作用影响的片段越长,更容易使整条链结构变得稳定而紧密。图3(c)为单个氨基酸带电量q为0.8C时回转半径随时间的变化,Rg的大小与M值呈负相关。和图3(a)和3(b)相比,M为5时回转半径随氨基酸带电量q的增大,其上升趋势更为明显,M为10、20、25时回转半径随氨基酸带电量q的增大略有上升,M为50时回转半径随氨基酸带电量q的增大有下降趋势,证实了图3(b)所总结出来的结论。图3(d)中可以看出,在单个氨基酸带电量q为1C的情况下,M为5的回转半径相较于q为0.8C的情况有小幅度上升,回转半径曲线的波动幅度从0.1 nm降至0.05 nm,M为10、20、25和50的回转半径变化较小。这表明,当蛋白质链上单个氨基酸带电量过大时,静电相互作用会使整条蛋白质链上带异种电荷的氨基酸牢牢吸附在一起,形成固定结构。

图3 蛋白质链在不同单个氨基酸带电量下回转半径随模拟时间的演化图Figure 3 Time evolution of radius of gyration on the protein constructed by residues with different charge

图4为氨基酸带4种电量情况下,蛋白质回转半径平均值与连续带电荷的氨基酸数目M的关系图。当M为5时,回转半径值与带电荷量q呈正相关,即,蛋白质的回转半径随着氨基酸带电荷的增加而增加。随着M增大,不同q值下的回转半径均值逐渐趋同,当M不低于25时,q值对回转半径影响较小。结合图3和图4得出结论:第一,在氨基酸带电量较小的情况下,蛋白质链的回转半径随连续带电荷的氨基酸数目变化的区分度不明显,随着氨基酸带电量的增大,在连续带电荷的氨基酸数目不同的情况下,蛋白质链的回转半径区分度增强;第二,随着连续带电荷的氨基酸数目的增大,不同蛋白质链回转半径差距越小。

图4 蛋白质链的回转半径与相同电荷氨基酸数目M的变化趋势图Figure 4 Radius of gyration of the protein constructed by the residues with charge q versus the number of sequentially changed residues M

图5给出在不同条件下构造的蛋白质链的典型构型图。其中,图5(a)(b)(c)分别给出了连续带电荷氨基酸数目M为5的情况下,单个氨基酸带电荷量q为0.05C、0.4C、1C三个条件下的蛋白质链的可视化结构图。在此条件下图5(a)(b)(c)的回转半径均值分别为0.86、1.07、1.74 nm,从数据上来看,回转半径均值随着q值增大而增大,说明蛋白质链的体系结构随着单个氨基酸带电荷量的增大变得越来越松散。我们从结构图中看出,图5(a)组成单个螺旋的珠子(氨基酸)数目在15～20之间,图5(b)中组成单个螺旋的珠子数目在10～15之间,图5(c)无螺旋结构,说明M为5的情况下蛋白质链随着带电荷量的增大逐渐从团簇状逐渐向长城状转变。图5(d)(e)(f)分别给出了连续带电氨基酸数目M为25的情况下,单个氨基酸带电荷量q为0.05C、0.4C、1C三个条件下的蛋白质链可视化结构图。在此条件下图5(d)(e)(f)的回转半径均值分别为0.84、0.79、0.76 nm,从数据上来看,回转半径均值随着氨基酸带电荷量q增大20倍的情况下仍然变化不大,说明M为25的情况下蛋白质链的体系结构受电荷量影响较小。从可视化结构图来看,图5(d)组成单个螺旋的珠子数目在50左右,图5(e)组成单个螺旋的珠子数目在15～20之间,图5(f)组成单个螺旋的珠子数目在10～15之间,说明M为25的情况下电荷量对蛋白质链的松散程度影响较小,但是组成蛋白质单个螺旋的氨基酸数目在减少。

图5 蛋白质链在不同M和q情况下的典型结构图Figure 5 Typical structural diagrams of protein chains under different M and q conditions

3 结 论

本文对一个含有200个氨基酸的蛋白质链进行粗粒化分子动力学模拟,通过研究体系能量和回转半径,对模拟结果得出以下结论:1)无论是改变链上连续带同极性电荷的氨基酸数还是改变单个氨基酸带电量,体系的范德华能与静电势能总是呈相反的变化趋势。总势能的变化趋势和静电势能的变化趋势相同,且静电势能绝对值远远大于键能和范德华能,所以体系非键相互作用的主导作用为静电相互作用;2)当体系中单个带电氨基酸带电量大于0.2C时,蛋白质链的回转半径随着同极性氨基酸的连续数目的减小而增大;3)蛋白质链的回转半径随着氨基酸带电荷量的增大而增大,且同极性氨基酸连续数量越小,回转半径随带电荷量的变化关系越明显。这些结论说明,蛋白质的三维结构主要是由沿蛋白质链相距较远但在空间上相互闭合的非键相互作用引起的,其中静电相互作用发挥了极大优势,这为理解蛋白质在不同静电相互作用下的结构特征及转变行为提供了理论依据,并为蛋白质结构预测提供了思路。