火炮回转半径测边网检测法及其误差分析

霍李，王媛，赵黎兴

(中国白城兵器试验中心，吉林白城137001)

火炮回转半径测边网检测法及其误差分析

霍李，王媛，赵黎兴

(中国白城兵器试验中心，吉林白城137001)

为提高火炮回转半径的测量精度，提出一种五垂点测边网检测方法，并对各误差源进行分析。首先，在火炮检测现场布设5个垂点的测边网;然后，通过测边网条件平差的方法对测量边长值进行平差处理，得到各测量边长的平差值;最后，用测量边长的平差值计算各点的相对坐标，并通过圆拟合得到火炮回转半径值。采用蒙特卡洛方法对各误差源进行模拟的结果表明:当标记点分布不均匀的角度均方差≤8°、火炮调平的角度均方差≤2°、铅垂摆动幅度和边长的测量均方差均不大于5 mm时，火炮回转半径的测量均方差≤3 mm。模拟结果验证该方法的可行性和有效性。

工程测量技术;火炮回转半径;测边网;蒙特卡洛方法

0 引言

火炮回转半径，即炮口到炮塔回转轴的距离［1］。在靶场试验中，需要测量火炮的回转半径来检查火炮状态是否偏离设计指标［2－4］或进行弹道修正［5－6］。由于直接测量法［7］在现场检测时可操作性差，通常采用间接测量方法。

目前，间接测量方法可分为“角度弦长法”和“测边网法”2类。由于角度弦长法需要测量弦长和对应的圆心角［7－8］，而在检测现场，炮塔旋转角(圆心角)的精确测量较为困难。测边网法避免了圆心角的测量，按垂点数量的多少可分为“三边法”(3个垂点)［9］和“大地四边形测边网法”(4个垂点)［10］。“三边法”是以3个垂点构成的三角形的外接圆半径为回转圆半径，无任何冗余测量数据，测量结果的精度完全取决于现场操作;“大地四边形测边网法”存在1条冗余数据。

为进一步提高火炮回转半径的测量精度，本文在文献［10］的基础上进一步增加冗余数据，探讨5个垂点的测边网检测方法的实现，并用Monte Carlo方法分析了测量过程中各误差源对结果的影响。

1 五垂点测边网法

1.1 内角与测边的关系

在图1的三角形中，lA、lB和lC为3条边的测量值，角A、角B和角C为对应的顶角。hA、hB和分别为角A、角A和角C至其对边的高。

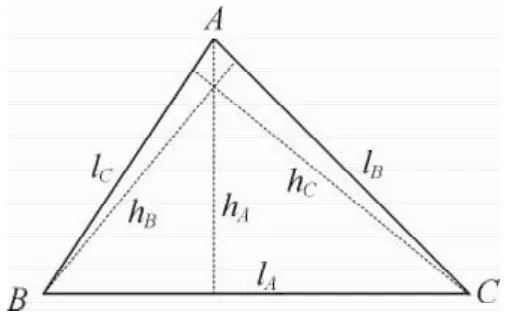
图1 测边三角形

可通过3条边的测量值计算出各顶角的大小。以角A为例，有如式(1)的关系式。

通过3条边的测量值和各顶角的计算值，可按式(2)计算出高。

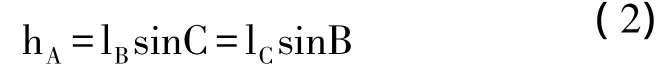
角A的角度改正数vA与边长改正数的关系式［11］如式(3)所示。

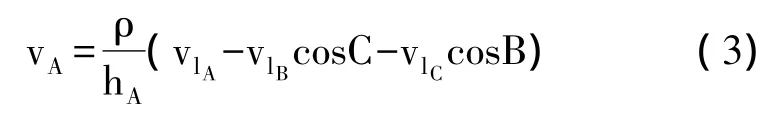
式中vlA、vlB、vlC为相应边长改正数;ρ≈206 264.8″，是弧度与角秒的换算系数。

1.2 五垂点测边网平差

图2 五点测边网示意图

图中，平差值条件方程如式(5)所示。

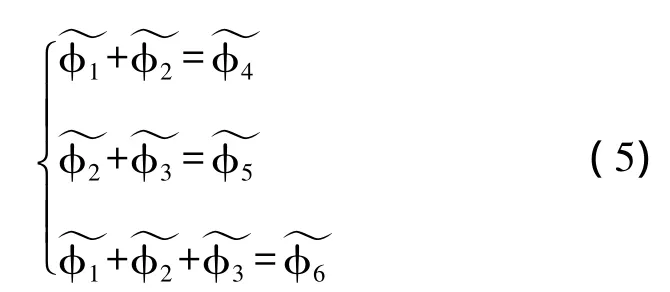
由式(4)和式(5)得到以角度改正数表示的图形条件，如式(6)所示。

式中，βa、βb、βc为角度闭合差，按式(7)计算。

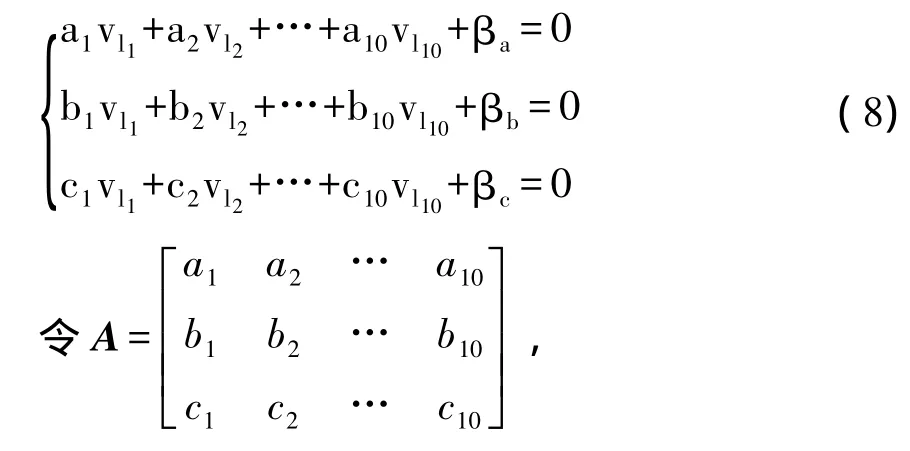
1.3 回转半径拟合

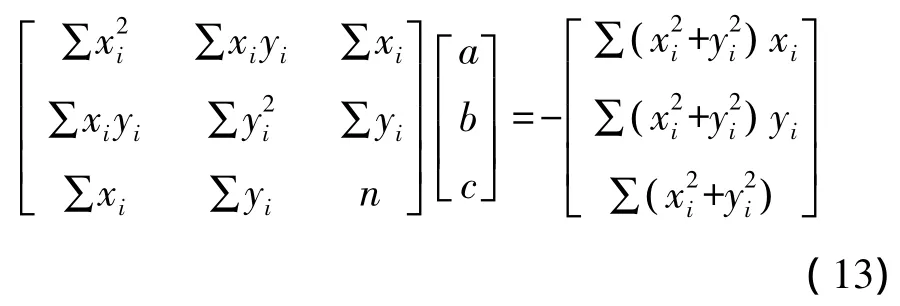
2 测量误差

该方法的测量误差包括火炮调平误差、水平地面上垂点位置误差以及各点之间的距离(边长)测量误差等。

2.1 标记点位置分布不均匀

式中，R为火炮回转半径;θi为相邻2个点间对应的圆心角，按式(15)计算

式中，σfi为点分布不均匀的圆心角误差，为指定范围内的任意随机值;θ1为[－π，π]范围内的任意随机值。

2.2 火炮调平误差

由于火炮调平误差的影响，实际状态下的火炮回转圆并不是绝对水平，可以看作是以回转圆的某个直径为转轴旋转α得到。以该旋转轴为x轴，在水平面上与x轴垂直相交的为y轴，在火炮回转圆所在平面上与x轴垂直相交的为y'轴，如图3所示。

图3 回转圆倾斜示意图

2.3 垂点位置标记误差

考虑到在标记垂点过程中，铅垂是绕投影点进行摆动的，因此垂点可以看作是在特定圆内的一点。该圆的圆心为投影点，半径为摆动幅度，如图4所示。

图4 垂点位置标记误差示意图

垂点位置标记误差在x轴和y轴上分别表示为σx和σy，按式(17)计算

式中，r为铅垂摆动幅度，为指定范围内的任意随机值;β为[－π，π]范围内的任意随机值。

2.4 测边误差

平面内任意两个点A( xA，yA)、B( xB，yB)之间的距离dAB，按式(19)计算

将式(18)的计算结果依次代入式(19)计算出各点之间的距离，考虑到边长测量误差σl，则按式(20)计算出各边的模拟值lk

3 各因素对测量结果的影响分析

影响测量结果的因素有4个，即火炮调平误差α、标记点分布不均匀的角误差σfi、铅垂摆动幅度r和边长测量误差σl。以五垂点法为例，用Monte Carlo法模拟抽样m=105次。取R=4 000 mm、n= 5，以现场可操作的σfi=5°、α=1°、r=2 mm和σl=5 mm为例，得到的火炮回转半径的测量均方差为1.22 mm，完全满足靶场试验的要求，这说明该方法在现场检测的可行性和有效性。

以上述各参数为基本条件，进一步分析各误差源对结果的影响趋势。

3.1 分布不均匀角误差σfi的影响

在基本条件的基础上，分别取分布不均匀角误差σfi为不同值时得到的火炮回转半径的测量均方差δR，结果如表1所示。

表1 分布不均匀角误差对结果的影响

由表可以看出:标记点分布不均匀的角误差σfi对火炮回转半径的测量结果影响不大，至少在σfi≤8°的范围内无显著影响。

3.2 倾角误差α的影响

在基本条件的基础上，分别取火炮调平误差α为不同值时得到的火炮回转半径的测量均方差δR，结果如表2所示。

表2 不同倾角误差对结果的影响

由表可以看出:随着火炮调平误差α的增加，δR呈上升趋势;特别是当α＞2°时，δR上升趋势越发明显。

3.3 铅垂摆动幅度r的影响

在基本条件的基础上，分别取铅垂摆动半径r为不同值时得到的火炮回转半径的测量均方差δR，结果如表3所示。

表3 铅垂摆动幅度对结果的影响

由表可以看出:随着铅垂摆动半径r的增加，δR呈上升趋势;特别是当r＞5 mm时，δR上升趋势越发明显。

3.4 边长测量误差σl的影响

在基本条件的基础上，分别取边长测量误差σl为不同值时得到的火炮回转半径的测量均方差δR，结果如表4所示。

表4 边长测量误差对结果的影响

δR/mm0.7020.7320.8071.2242.1224.094

由表可以看出:随着边长测量误差σl的增加，δR呈上升趋势;特别是当σl＞5 mm时，δR上升趋势越发明显。

取σfi=8°、α=2°、r=5 mm、σl=5 mm，其他条件不变，得到火炮回转半径测量均方差为2.44 mm，完全满足检测需求。这说明该方法在保证有效性的前提下，进一步提高了在现场检测的可行性。

4 结束语

本文提出的五垂点测边网法实现了火炮回转半径测量。通过Monte Carlo方法对各误差源进行模拟的结果表明，在现场可操作的情况下，火炮回转半径的测量均方差＜3 mm，完全满足检测需求。

［1］车琳.火炮静态检测技术［M］.北京:国防工业出版社，2010:218.

［2］毛保全，穆歌.自行火炮总体结构参数的优化设计研究［J］.兵工学报，2003，24(1):5－9.

［3］蔡文勇.大口径车载火炮多柔体动力学与总体优化研究［D］.南京:南京理工大学，2009.

［4］王宝元，衡刚，周发明，等.炮塔转动阻尼系数试验测试技术［J］.火炮发射与控制学报，2013(1):67－70.

［5］郝玉生.动态弹道补偿［J］.火力与指挥控制，2003，28 (5):92－94.

［6］黄义，汪德虎，王建明，等.舰载跟踪雷达测量弹道修正弹坐标转换模型［J］.兵工自动化，2012，31(8):3－5.

［7］中国人民解放军总装备部司令部.火炮静态检测方法: GJB 2977A－2006［S］.北京:总装备部军标出版发行部，2008.

［8］霍李，江明义，李典，等.火炮回转半径测量中瞄准镜的最佳装定角［J］.兵器试验，2012(4):55－59.

［9］霍李，王媛，赵春宇，等.三边法测量火炮回转参数［J］.兵器试验，2014(1):50－52.

［10］霍李，王媛，赖富文，等.基于测边网的火炮回转半径检测方法［J］.火炮发射与控制学报，2014，35(3):74－77，82.

［11］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.2版.武汉:武汉大学出版社，2009:75－92.

(编辑:刘杨)

Measurement method and error analysis of artillery rotation radius by trilateration network

HUO Li，WANG Yuan，ZHAO Lixing
(Baicheng Ordnance Test Center of China，Baicheng 137001，China)

In order to improve the measurement accuracy of the artillery rotation radius，a kind of method based on trilateration network with five vertical points was proposed，and the error sources were analyzed.Firstly，the trilateration control network with 5 vertical points was established in the testing field.Secondly，the adjustment value of every side was acquired by use of the method of trilateration network condition adjustment.Finally，the relative coordinates of each point was calculated by using the adjustment value of every side，and the artillery rotation radius value was obtained by use of the circle fitting.The simulation results come from Monte Carlo method show that when the angle measurement of marking the no－uniform distribution of the mean square deviation is not more than 8°，the artillery adjustment flat angle of mean square deviation of not more than 2°，the plumb swing amplitude and the side length of the measurement variance were not more than 5 mm，artillery rotation radius of the measured mean square error is less than 3 mm.The results show that the method is feasible and available.

engineering survey technology;artillery rotation radius;trilateration network;Monte Carlo method

A

1674－5124(2016)11－0027－04

10.11857/j.issn.1674－5124.2016.11.006

2016－4－22;

2016－06－17

国家军用标准修订项目(14ZS021)试验技术理论研究(12－sy14)

霍李(1979－)，男，重庆市人，工程师，硕士，主要从事火炮静态检测技术研究。