三维结构形变的单目像机测量方法

张林龙，张伟，胡昌华，周志杰

(1.火箭军工程大学302室，陕西西安710025; 2.火箭军工程大学403室，陕西西安710025)

三维结构形变的单目像机测量方法

张林龙1，张伟2，胡昌华1，周志杰1

(1.火箭军工程大学302室，陕西西安710025; 2.火箭军工程大学403室，陕西西安710025)

针对大型结构形变的摄像测量中，双目系统结构复杂、成本高、特征点匹配度低，而传统单目测量系统不能有效获取目标深度信息等问题，借助平面反射镜提出一种新的单目像机三维形变测量方法。首先，基于平面反射镜的光学反射原理构建单目三维测量模型;其次，利用像机与平面镜的内在参数推导出单目像机视图下的极线约束关系;然后，在测量系统完成参数标定的情况下，将极线约束关系作为约束条件引入利用基于LM算法的改进光束法平差进行结果优化，完成三维目标点的位置精确测量，进而实现大型结构的形变测量。仿真实验与实际测量实验结果表明单目像机测量方法的有效性与优越性，具有实际工程应用价值。

单目测量;极线约束;光束法平差;形变测量

0 引言

大型结构件如运载火箭、飞机、舰船、风电叶片、储油罐、桥梁等由于几何形状、载荷条件和工作环境的复杂性，必须进行结构静力实验来研究其在静载荷作用下的强度刚度和稳定性等问题，因此测量大型结构的形变成为监测设备性能的重要因素［1］。摄像测量方法由于其高精度、非接触等特点广泛应用于形变监测［2］。

目前摄像测量方法可分为双(多)目像机测量与单目像机测量。对于目标点的三维位置测量主要运用三维交会测量原理，至少需要两台摄像机［1］。利用双目像机进行交会测量需要对相同特征点进行匹配，在匹配过程中易出现误匹配、漏匹配等严重影响测量精度的问题。而单目像机只能确定目标点所在直线，不能得到目标点的深度信息，常用于平面测量，但是也存在利用单目像机借助其他设备进行三维测量的方法，黄小云等［3］利用一种放置于摄像机前方的立式靶标建立图像纵坐标与实际成像角度之间的映射关系，结合几何投影关系实现深度信息的实时提取;晁志超等［4］在摄像机光轴方向上安装高精度激光测距传感器实现单目像机测量目标姿态的目的;K.Kawasue等［5－6］根据像机距离被测目标远近测得光线数量不同或者利用拍摄高速旋转电子束分裂器所得图像内的光圈半径大小来获取深度信息;冯晓锋等［7］在测量点附近合适位置放置平面反射镜，通过单目像机拍摄实际物体及镜面成像来提取目标点三维位置信息。对于大型结构件而言其结构复杂，在对目标区域进行监测时双目像机布置复杂，测量系统价格较高;单目像机可以解决测量系统的复杂性问题但是大型结构的变形量微小，要求测量精度较高，因此在上述研究的基础上进一步研究结构形变的高精度单目测量具有重要意义。

1 问题描述

目标点的摄像测量原理如图1所示，O为摄像机的光心，空间目标点P为在世界坐标系Qw－XwYwZw下的坐标为(xw，yw，zw)，其在摄像机中的成像点为P1(x1，y1)。根据理想针孔成像模型，像点P1、光心O、物点P三点共线，即满足式(1)共线方程:

图1 摄像测量原理

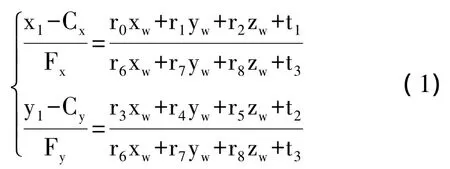
式中:(Cx，Cy)—图像主点;

(Fx，Fy)—等效焦距;

r0，r1，…，r8和t1，t2，t3—世界坐标系变换到像机坐标系下的旋转矩阵R和平移向量T的元素。

在像点坐标(x1，y1)和像机内外参数已知的情况下，式(1)是关于xw、yw、zw的非线性方程组。由于单个像机只能获取两个方程而方程组中存在3个未知数，所以得不到目标点的位置，只能确定其在通过像机光心和像点的空间直线上。

基于以上问题的考虑，利用单目像机测量三维目标位置需要解决以下问题:1)建立单目像机测量模型，增加方程数目，提供有效的深度信息;2)构建合理的约束关系进行结果优化，满足高精度测量要求。

2 单目像机三维测量理论

平面反射镜价格低廉，同时可以近似完全呈现被测点的全貌，因此考虑利用平面反射镜代替部分像机，建立近似于双目测量系统的单目测量系统。

如图2所示，假设存在平面反射镜S，在平面镜内建立虚拟世界坐标系O'w－x'wy'wz'w，l为两世界坐标系原点之间的距离，则虚拟世界坐标系与世界坐标系满足关系式:

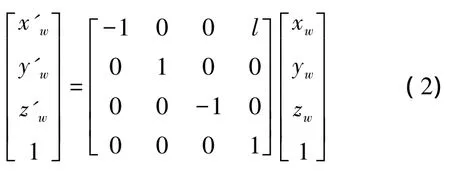
假设世界坐标系中齐次坐标为P的空间点在光心为Ocr的像机投影像点齐次坐标分别为P1、P2;在虚拟坐标系中的对应镜面成像点的齐次坐标为P';在虚拟光心Ocv的像机投影像点齐次坐标为P'2。令K为像机内参数矩阵;RT1、RT2分别为由相应的旋转矩阵R1、R2以及平移向量T1、T2构成的4×4参数矩阵;Zc、Z'c为相应物点到光心的距离在光轴方向的投影。

图2 单目像机三维测量模型

由摄像测量原理可知，世界坐标系中被测点P(xw，yw，zw)与像点P1(x1，y1，z1)满足关系:

点P对应的镜面成像点P'(x'w，y'w，z'w)与实际像机成像点P2(x1，y2)满足关系:

由式(2)、(4)可得到被测点与图像点满足关系式:

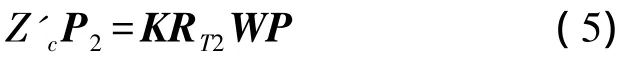
至此得到单目像机的测量模型，由式(3)、(5)可组成含有4个方程的新共线方程组，在已知像机内外参数的情况下，通过最小二乘法求解方程组中3个未知数即可求出被测量目标点的三维位置。

3 单视图极线约束下的改进光束法平差

在实际测量过程中由于光线、温度以及测量设备等因素的影响，理想条件下的测量结果不能满足大型结构形变的高精度要求。光束法平差作为摄像测量领域保证高精确测量结果的最重要理论和方法，被公认为是各种算法中精度最高的方法［2］。本节根据实际像机与虚拟像机的位置关系建立同一视图下的单目极线约束关系，然后结合LM算法对光束法平差进行改进达到优化测量结果的目的。

3.1 单视图下的极线约束关系

假设像机图像分辨率为mpixel×npixel，由图2可知，虚拟像点P'2(x'2，y'2)与实际像点P2(x2，y2)属于对称关系，即满足关系式:

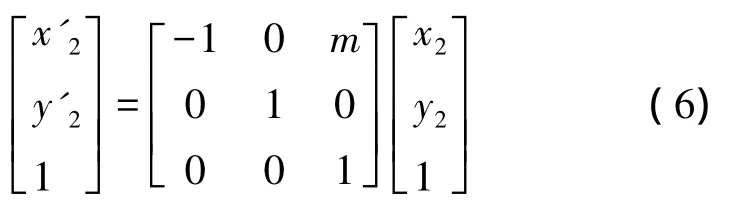
式(6)在齐次坐标下的关系式可以表示为:

因此根据式(5)、(7)可得点P(xw，yw，zw)到虚拟像机的成像点P'2(x'2，y'2)在齐次坐标下投影成像关系为:

即相应的投影矩阵M'2为:

设光心Ocr齐次坐标为［xCyCzC1］T，则两光心之间距离OcrOcv为|l－2xC|，至此可得光心Ocr在虚拟图像中的对应像点即虚拟极点e'=(1/ |l－2xC|)M'2［xCyCzC1］T;根据文献［2］可得到基础矩阵:

式中:M+——点P到点P1的投影矩阵M的伪逆;

［e'］×——由极点e'=［e0e1e2］T构成的秩为2的反对称矩阵:

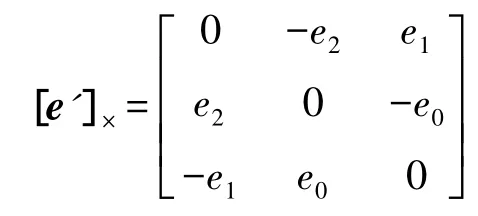
于是可以得到利用基础矩阵F描述的同一幅视图下的极线约束关系:

3.2 基于LM法的光束法平差测量

光束法平差实质上是通过高斯牛顿法进行最优估计的方法，在大量有效初始值的情况下高斯牛顿算法可以保证快速收敛，是一种有效的主流算法。本文单目像机测量系统求解的初始值是在理想条件下所得，控制点精度过低，利用高斯算法实现光束法平差容易出现不稳定、精度较低的解，甚至无法收敛。本文将LM算法［8］、阻尼策略和验后权估计［9］运用于三维形变测量的光束法平差中，并将单目视图下的极线约束关系作为约束条件，克服高斯牛顿算法的收敛性缺陷，提高目标点的定位精度［10］。

在考虑像差情况下的共线方程可表述为

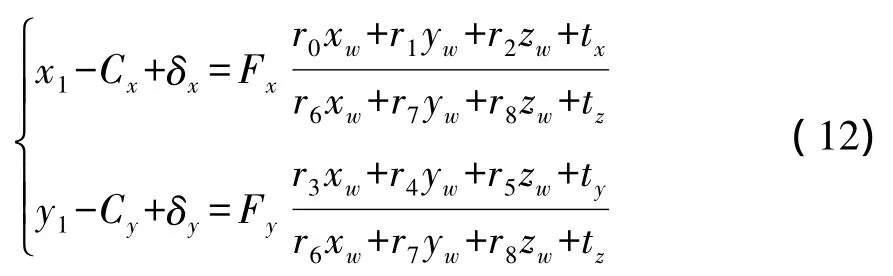
式中像差按照式(13)计算模型，k0、k1、k2、k3、k4为镜头畸变系数。

因测量结构形变时测量设备固定，而像机内参数将成为影响测量结果的重要因素，所以本文选取像机内参数(Fx，Fy，Cx，Cy)及目标点三维坐标(xw，yw，zw)作为平差参数。根据光束法平差将式(12)对平差参数进行一阶线性化后，可用矩阵符号表示误差方程式为

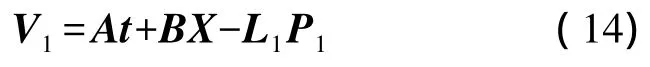
同理将单视图下的极线约束关系式(11)化为:

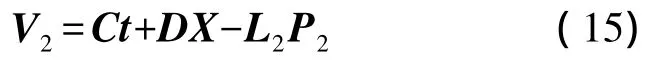
式中:t——像机内参数向量;

X——待定点的空间三维坐标;

A、B、C、D——分别为其相应的系数矩阵;

L1、L2——像点坐标观测值向量;

P1、P2——像点观测值矩阵;

V1、V2——像点坐标观测值改正数。

根据LM算法标准方程式建立式(14)、(15)对应的法方程:

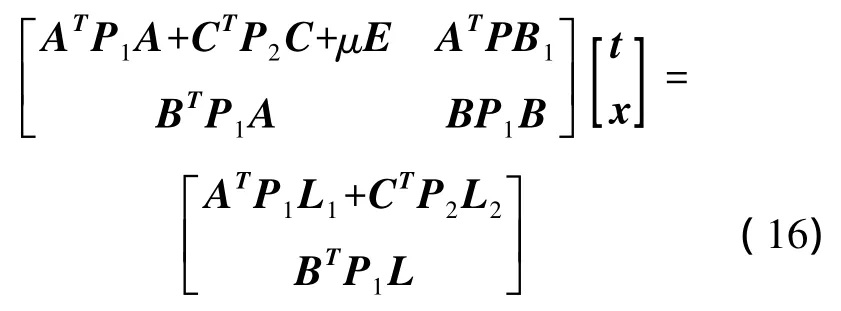
式中:E——为单位矩阵;

P1——权矩阵，代表像点坐标观测值的权;

μ——阻尼策略中的阻尼系数。

迭代求解式(16)的过程中可以通过验后估计权值的方法进一步确定，在平差过程中，采用平差权函数:

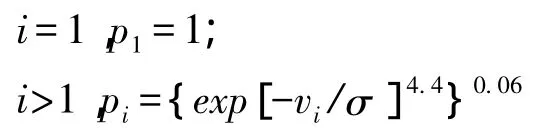
式中:i——迭代次数;

vi——像点坐标的改正数;

在对u设定合适初值的情况下，在迭代过程中根据LM法更新u值，对式(16)进行迭代求解，求得平差优化的最终结果X。

4 单目像机三维测量实验

为了验证本文提出测量方法的正确性和有效性，进行了仿真实验与室内测量实验，并将测量结果与传统双目摄像测量方法进行了精度比较。

4.1 仿真实验

首先建立大型三维曲面模型，对其进行网格化，其中网格大小为1.88 cm×0.25 cm，以网格角点作为标志点，在模型标志点以及像点分别引入均值为0、均方差为0.2 mm与0.02pixel的噪声，获得仿真图3，其中右半部分为平面反射镜内图像。在视觉库opencv基础上利用Visual C++6.0进行测量程序编译。

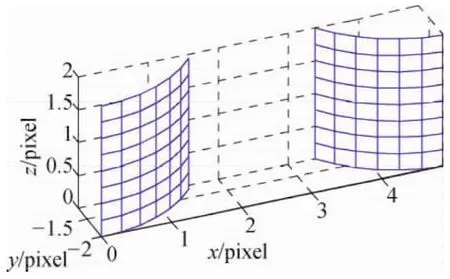
图3 三维曲面模拟图

实验过程中利用本文提出的单目像机测量方法与传统双目像机测量进行三维测量，在模拟测量系统内外参数不变的情况下获取60组画面，图4分别为沿x、y、z轴实际测量位置与模拟位置之间的平均误差。

图4 测量误差

由测量结果可知，本文单目像机测量方法基本可以满足大型结构目标点的测量要求。图4(a)显示两种测量结果沿x轴精度均在0～1 mm之间。从图4(b)、4(c)来看，本文单目像机测量方法相比较传统双目测量方法而言在沿y轴方向深度信息获取方面误差较大，但也基本低于2.5 mm;z轴方向测量精度相对较高，不仅如此在3个坐标轴方向测量结果上z轴误差也相对较低。

4.2 室内测量实验

在室内墙角粘贴间隔1.12 cm×1.12 cm的棋盘格作为标识物，通过监测棋盘格角点位置即可实时测量出结构形变。由于实验受限，本实验通过比较测量目标点位置与实际位置确定测量效果。

首先对mvc1500NIR像机内参数进行标定，将平面棋盘格靶标作为标定板，通过变化像机位置与角度进行图像拍摄，采用文献［11］标定法进行标定，标定结果如表1所示。

表1 像机内参数标定结果

重新固定像机位置，调整平面反射镜位置，使像机可以通视被测量目标及反射镜。采集图像，对测量系统外参数进行标定，虚拟像机相对真实像机外参数即旋转矩阵R、平移向量T标定结果如下:

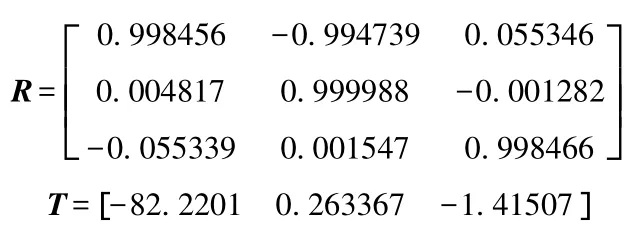
图5 实验采集图像

利用像机与平面反射镜对表面粘贴有棋盘格标志的结构件表面进行图像获取，通过合理设置反射镜与像机的位置使像机能够通视实际表面与反射镜内的虚拟表面，采集的图像如图5所示。

基于上述标定结果在Matlab中进行三维目标点测量，利用亚像素定位方法进行角点精度定位，对检测到的16对特征点进行精确匹配后，采用改进的光束法平差后的部分目标点位置与实际位置如表2所示。其中RMS为目标点实际位置与测量位置之间的距离误差。

4.3 结果讨论与分析

仿真和室内测量实验验证了单目像机三维测量理论的正确性与可行性。实际测量结果趋势与仿真实验趋势基本相同，都反映了单目像机测量系统在获取三维深度信息方面误差相对较大，但测量误差基本低于0.8 mm。由于本文室内场景实验过程中采用的是普通平面反射镜，将其视为理想状态必然会影响最终测量精度，这也是深度信息提取方面精度低于传统双目测量系统的主要原因。

5 结束语

本文针对大型结构形变的单目摄像测量方法展开深入研究，借助平面反面镜的作用实现了单目像机的有效测量。基于平面镜成像的单目像机测量理论解决了测量过程中深度信息丢失的问题，在双目像机测量理论的基础上提出的同一视图下的单目像机极线约束关系为利用LM算法的改进光束法平差的求解提供约束。仿真实验表明本文提出的单目像机三维测量精度与传统双目像机精度相当。室内场景实验表明本方法具有可行性，可以应用于大型结构的三维形变测量等实际工程方面，能够提高测量系统的经济性与实用性。但是在测量前要合理布置像机与平面镜相对被测目标点的位置，确保像机能够同时获取实际目标和反射镜内的目标点，这也是本文单目像机测量系统在仪器设置灵活性方面有待改进之处。

［1］周翔，胡建，孙林涛，等.大型结构变形实时摄像测量方法［J］.实验力学，2012，27(4):503－510.

［2］于起峰，尚洋，伏思华，等.大型结构变形及形貌摄像测量技术研究进展［J］.实验力学，2011，26(5):479－490.

［3］黄小云，高峰，徐国艳，等.基于单幅立式标靶图像的单目深度信息提取［J］.北京航空航天大学学报，2015，41 (4):649－655.

［4］晁志超，伏思华，姜广文，等.单目摄像机－激光测距传感器位姿测量系统［J］.光学学报，2011，31(3):85－91.

［5］OYA Y，KAWASUE K.Three－dimensional quantitative visualizationfromasingleimage［J］.Sensors＆Transducers，2009(7):142－154.

［6］KAWASUE K，NAGATOMO S，OYA Y.Three dimensional measurement of aquatic organisms using a single video camera［J］.Sensors＆Transducers，2010(6):118－126.

［7］FENG X，PAN D.Research on the application of single camera stereo vision sensor in three－dimensional point measurement［J］.Journal of Modern Optics，2015(62):1－7.

［8］祝强，李少康，徐臻.LM算法求解大残差非线性最小二乘问题研究［J］.中国测试，2016，42(3):13－15.

［9］李德仁，袁修孝.误差处理与可靠性分析［M］.武汉:武汉大学出版社，2002:240－255.

［10］马友青，贾永红，刘少创，等.基于LM法的光束法平差巡视器导航定位［J］.东北大学学报(自然科学版)，2014，35(4):489－493.

［11］朱焱丹，廖俊必，何子牛.基于LabVIEW的机器视觉系统的标定［J］.中国测试，2009，35(6):54－56.

(编辑:李刚)

The 3D structure deformation measurement method based on monocular camera

ZHANG Linlong1，ZHANG Wei2，HU Changhua1，ZHOU Zhijie1
(1.302 Unit，Rocket Force University of Engineering，Xi’an 710025，China; 2.403 Unit，Rocket Force University of Engineering，Xi’an 710025，China)

Binocular measurement system has the problem of complexity，high price，low matching precision in the deformation measurement of large－scale structure.Meanwhile，traditional monocular system cannot obtain depth information of 3D(three dimensional)object.A new method for measuring the 3D deformation that uses a single video camera utilizing a planar reflector was proposed in this paper.Firstly a monocular measuring model of 3D object was founded utilizing the reflective principle of planar reflector.Then an epipolar geometry inhibition equation in the same video camera view was settled by inherent parameters of camera and reflector.The measured point was located accurately by the improved bundle adjustment based on LM algorithm after the intrinsic and extrinsic camera parameters of the measurement system were calibrated.So the deformation measurement of large－scale structure was achieved.Both simulation and indoor experiments results validate that the proposed measuring technique is effective and has the realism value in engineering applications.

monocular;epipolar geometry inhibition;bundle adjustment;deformation measurement

A

1674－5124(2016)11－0017－06

10.11857/j.issn.1674－5124.2016.11.004

2016－03－02;

2016－04－07

国家杰出青年基金(61025014);国家自然科学基金(61174030，61104223，61374120)

张林龙(1991－)，男，河南驻马店市人，硕士研究生，专业方向为诊断技术及自动化装置。