基于双分支融合学习和二次图结构优化的点云配准算法

祝 磊,叶海良,杨 冰,曹飞龙

(中国计量大学 理学院,浙江 杭州 310018)

与刚性变换相关的点云配准,作为3D计算机视觉和图形学中基本但关键的研究方向,在许多视觉领域都发挥着重要作用,例如姿态估计[1-2]、3D对象重建[3]、自动驾驶[4-5]等。点云配准旨在通过预测一个变换矩阵来对齐两个不同空间中的点云。在这个过程中,检测两个点云之间正确的对应点对是必不可少的。然而,由于噪声和遮挡,点云中的某些点在另一个点云中没有对应点,使得点云配准在复杂的实际应用中仍然是一个极具挑战性的问题。

点云配准任务一般可分为三个阶段[6]:首先对两个点云进行特征提取,分别获得潜在的判别性特征;其次在对上述特征进行再处理的基础上,得到两个点云之间的对应关系;最后通过奇异值分解(singular value decomposition,SVD)计算变换矩阵,对两个不匹配的点云进行对齐。

近年来,深度学习已经成功应用于端到端的点云配准。Wang等[7]将动态图CNN(dynamic graph CNN,DGCNN)[8]挖掘的结构特征输入到带有指针网络的transformer中来计算两个点云间的点对关系。在迭代配准过程中,Li等[9]结合几何和距离特征计算可靠的相似度得分,同时提出两阶段点消除技术,在当时实现了性能和效率双赢。随后,Fu等[10]采用基于交互transformer与图神经网络(graph neural networks, GNN)[11-12]结合的方式进行上下文聚合,并应用最优传输技术获得可靠的匹配矩阵。最近,Yew等[13]将由核点卷积[14]学习到的嵌入输入到由自注意力和交叉注意力构成的网络中,在没有显式特征匹配的情况下实现了所需的刚性变换预测。尽管以上成就在点云配准方面取得了很大的突破,但它们倾向于关注整体配准框架和深度特征交互,而不是力图去细化对应关系。

对于基于深度学习的点云配准,获取节点与节点间的正确的对应关系是配准成功的关键,而这往往是由所提取特征的质量决定的。只要得到足够准确的对应点对,通过SVD就可以很容易地计算出未知的刚性变换。从任务的角度来看,挖掘合适的判别性特征、优化初始对应尤为重要。

为了挖掘点云丰富的特征表示,许多研究人员针对不规则的无序点云开发了许多特征提取方法。GNN能够有效地处理不规则数据,在知识图谱[15]、推荐系统[16]等方面展示出了强大的特征挖掘能力。由于点云也是一种不规则且非结构化的数据,因此,基于图的方法也比较适合点云。DGCNN、图关注卷积(graph attention convolution,GAC)[17]、串行关注卷积[18]倾向于在局部图结构中设计不同的卷积操作来提取点云的潜在特征。然而,上述方法均利用相邻点的特征来重建中心点的特征。与以往仅在邻居节点之间建立图结构不同,本文跳出这种模式,寻求凝聚中心点和邻居点特征的更高级的代理点间的图结构。这样,每个代理点将会具有更广的视野,有利于窥探局域图结构以及捕捉每个中心节点有效的判别性表示。

为了达到上述目的,本文利用图的思想构建了一种基于局域自适应投票的图卷积来挖掘点云潜在的判别性语义和结构特征。该卷积首先在局部邻域中构建富含中心点特征和邻居点特征的代理点,针对具有更广视野的代理点,设计自适应投票的方式学习代理点间的邻接矩阵,即结合坐标和特征自适应地学习每个代理点有边相连的投票,并根据投票得分计算邻接矩阵,同时也使每层的邻接矩阵能够随着特征的更新进行动态调整,以便使其朝着配准所需的方向更新。设计的基于自适应局域投票的方法,可以让学习到的局部邻接矩阵更好地反映出局部特征空间中潜在的图结构。接着,利用图卷积网络(graph convolutional networks, GCN)[19]来交流和聚合代理点间的信息。最后,将上述获得的局部几何特征与每点独立变换获得的特征进行融合,从而减少先前信息的丢失以及减缓GCN所具有的结构平滑现象,以增加获取特征的判别性。

另外,为了进一步缩小两个点云的图结构之间的点对特征差异以及缓解深度图卷积网络造成的匹配模糊,本文采用了一种针对对应矩阵的二次约束技术。具体地,本文考虑在深度图匹配中嵌入二次结构约束,最大化由深度特征学习到的两个邻接矩阵之间的一致性,从而减小两者之间的差异性,达到优化对应矩阵的目的。故而找到两个点云间的近似最佳的节点匹配,实现较高的配准性能。

1 本文所提出的方法

点云配准旨在预测一个旋转矩阵R∈SO(3)和一个平移向量t∈3。给定源点云X={xi∈3|i=1,2,…,N}和目标点云Y={yi∈3|i=1,2,…,M}。图1展示出了本文所设计的点云配准的整体框架。

1.1 双分支融合学习

对应矩阵的准确性决定着配准的精确性,而前者往往建立在有效的特征学习上面。为了获取到有效的高维节点特征,本文利用图的思想设计了一种基于局域自适应投票的图卷积来挖掘点云潜在的判别性特征。该卷积首先在局部邻域中构建富含中心点特征和邻居点特征的代理点。针对获得的代理点,采用自适应投票的方式学习代理点间的图结构,并利用GCN更新和聚合代理点间的特征。由于每个代理点都凝聚了中心点和邻居点特征,这将会使每个代理点具有更广的视野,以捕捉到每个局部邻域的可靠的邻接矩阵。上述过程被简化在图2中。由于代理点的学习机制是根据原始坐标和学习到的特征实现的,那么随着网络层数改变,邻接矩阵也会随着动态调整,以便使其朝着配准所需的方向更新。设计的基于自适应局域投票的方法,可以让学习到的局部邻接矩阵更好地反映出局部特征空间中潜在的图结构。此外,将上述获取的节点特征与直接对节点进行多层感知机(multi-layer perceptron,MLP)变换所获得的特征进行融合,在抽取局部几何信息的同时保留每点独立的语义信息,形成图3所示的双分支融合学习(dual-branch fusion learning, DBFL)模块,达到减少先前信息的丢失以及减缓GCN所具有的结构平滑现象的目的,以此来突出节点特征的判别性。

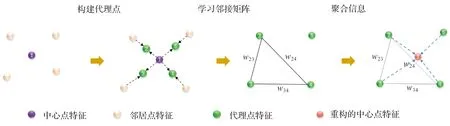
图2 基于自适应局域投票的图卷积的简化图示Figure 2 A simplified illustration of graph convolution based on adaptive neighborhood voting

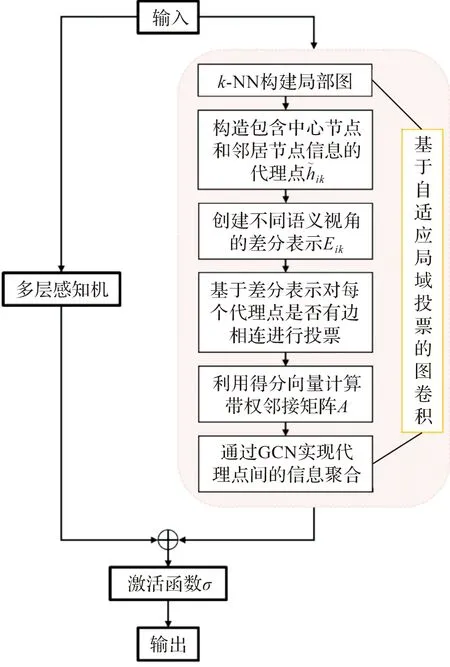
图3 双分支融合学习模块Figure 3 Dual branch fusion learning module

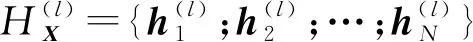
(1)

式(1)中cat[·,·]表示按通道拼接操作,φ1(·),φ2(·)是由不共享的MLP实现,W是一个可学习的参数矩阵。接着,通过下述简单的方式预测每个代理点有边相连的可能性,并将可能性大于0的代理点作为能够为局部图结构做贡献的有边点,否则为无边相连的孤立点:

oik=tanh(f(Eik))∈k,

(2)

wik=max(0,oik)。

(3)

式(2)中,f(·)表示一元函数。于是,可通过wik来衡量一个局域内代理点间带权的邻接矩阵A:

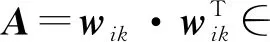
(4)

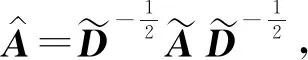
(5)

式(5)中,W′是一个可学习的参数矩阵,σ(·)表示一个激活函数。基于自适应局域投票的图卷积的具体过程可以参见算法1。

算法1:基于自适应局域投票的图卷积输入:给定坐标点xi∈X,及其在第l层对应的特征对应的特征hi;输出:重构特征hi。1.通过k-NN构造关于xi的局部邻居点集N(xi)={xik|k=1,2,…,K}及其对应的特征集N(h(l)i|k=1,2,…,K},h(0)i=xi;2.构建局域中坐标间和特征间的相对关系:Δxik=xik-xi,Δhik=h(l)ik-h(l)i;3.构建凝聚中心点和邻居点特征信息的代理点:hik=φ(Δhik);4.构建包含不同语义的差分表示:Eik=cat[Δxik,φ(Δhik,φ1(h(l)ik)-φ2(h(l)i)]W;5.通过对Eik进行自适应学习获得每个代理点有边相连的投票:oik=tanh(f(Eik))∈ℝk,wik=max(0,oik);6.根据投票得分计算代理点间潜在的邻接矩阵:A=wik·wTik∈ℝk×k;7.通过GCN更新和聚合局域特征:h(l)i=∑Kk=1σ(AhikW')。

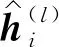
(6)

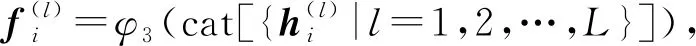
(7)

式(7)中,φ3(·)是由一个MLP实现。同样的,对于目标点云Y,FY可按照FX的计算方式得到。

1.2 特征交互建模及对应生成

为了更好地实现两个点云间的特征交互以及获取后续用于对应优化的全局邻接矩阵,本文采用文献[9]中的方式来计算两个输入点云各自的全局邻接矩阵AX和AY:

AX=s(Tr(FX,FY)(Tr(FX,FY))T),AY=s(Tr(FY,FX)(Tr(FY,FX))T)。

(8)

式(8)中,Tr(·)表示交互transformer更新,s(·)是一个softmax函数,使每条边都具有一个权值以衡量其重要性。对于所获得的全局邻接矩阵,利用单层GNN对每个点云进行特征更新,并将两个点云更新后的全局特征分别记为GX和GY。在此基础上,采用一个包含可学习参数的矩阵Ws∈C×C来构建两个点云中节点间的对应关系:

(9)

为了方便,本文将上述过程赋给一个统一的操作算子FIMCG(·),即有

AX,AY,C=FIMCG(FX,FY)。

(10)

1.3 基于Frank-Wolfe算法的二次图结构优

为了明确地利用图结构信息获取精确的对应关系,本文通过最小化两个图结构间的点对结构差异来细化匹配矩阵。对于Koopmans-Beckmann’s QAP[22],可以在最小化两个邻接矩阵间的不一致性的同时优化对应矩阵,以便使优化后的对应矩阵更加接近真值矩阵(ground truth)。具体地[25]:

(11)

其中AX∈N×N,AY∈M×M分别是GX和GY中编码边信息的邻接矩阵,Ms∈N×M衡量两幅特征图的节点相似度,‖·‖F表示矩阵范数。这里,将式(10)得到的可学习的矩阵C作为对应矩阵M的初始值,即M0=C,由于C为节点相似度矩阵,所以Ms=C。

接下来,本文采用一种和文献[25]相同的可微Frank-Wolfe算法[24]来优化q(M),以便获得一种更可靠的近似解:

vz+1←fsh(vz+1),Mz+1←(1-λz)Mz+λvz+1。

(12)

Mrefined=fsh(α·Mopt+β·C)。

(13)

式(13)中α,β均为可学习的参数。算法2提供了完整的配准算法流程。

算法2:基于双分支融合学习和二次图结构优化的点云配准算法输入:源点云X,目标点云Y,邻居节点数k,迭代次数T和Z;输出:对应矩阵Mrefined。1)特征提取:双分支融合学习DBFL(·)FX←DBFL(X,k),FY←DBFL(Y,k);2)特征交互建模及对应生成FIMCG(·)AX,AY,C=FIMCG(FX,FY);3)二次图结构优化M←C;for iter=0: Tdofor z=0: Z dov←argminv∇q(M)Tvv←fsh(v); //Sinkhorn正则化M←(1-λ)M+λv,λ=2/(z+2);end forend forMrefined=fsh(α·M+β·C); //α和β是可学习的参数输出:Mrefined。

因为优化的过程主要是利用两个点云的图结构信息,这样在训练过程中仅少数次的迭代就能达到一个比较精确的配准效果。由于原始的输入点云中包含噪声和离群点,这可能不是一个全局最优解,但是全局最优解可能也并不是本文所渴望得到的最佳匹配。对于Mrefined,本文按照参考文献[9]中的处理方式来计算所需的变换参数,实现点云配准。

2 实验及结果分析

2.1 损失函数及评价指标

本文采用了与RGM中相同的针对预测的对应矩阵Mrefined的交叉熵损失。这可以更好地监督网络学习到正确的匹配点对。具体的交叉熵损失函数描述如下:

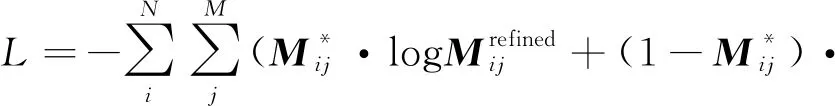
(14)

式(14)中M*表示对应矩阵的真实结果(ground truth)。图4直观地展示了损失函数值随训练轮数的变化趋势。和大多数文章类似,本文应用旋转矩阵R和平移向量t的平均绝对误差(mean absolute error,MAE)、R和t的平均各向同性误差(mean isotropic error,MIE)、R和t的均方根误差(root mean squared error,RMSE)来衡量变换参数的性能。此外,由于现实条件的配准是不知道两个点云间的平移向量和旋转矩阵的,因此,本文还采用了RGM使用的经裁剪的CD(clip chamfer distance, CCD)这一客观指标来衡量所提方法的优越性。

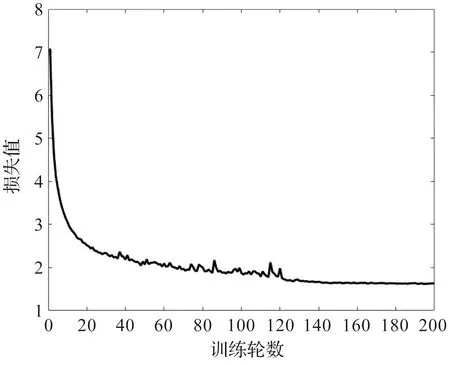
图4 损失函数值随训练轮数的变化趋势Figure 4 Trend of losses with the number of training epochs

2.2 数据集处理及实验设置

本文通过大量的实验分析了所构建的模型在点云配准中的优异性能。数据集和预处理描述如下。

ModelNet40[26]数据集是一个以物体为中心的合成数据集,广泛用于3D点云配准。它由12 311个CAD模型组成,涉及40个物体类别。实验中,每个点云均是从其对应的网格面中随机抽取2 048个空间坐标点,并转化到一个单位球体。此外,本文对每个物体点云再随机采样1 024个点作为源点云X,然后为X分配一个随机变换以获得目标点云Y,最后打乱两个点云中的点顺序。为了探索模型对噪声的抵抗力,每个点云都被添加了来自分布为N(0,0.012)并被裁剪到[-0.05,0.05]区间的高斯噪声。除非另有说明,否则上述设置默认应用于所有实验。

本文模型由SGD优化器训练200个epochs,初始学习率为0.001,采用多步学习率调整策略,分别在第120和140 epoch时进行学习率的调整。所有的实验都在一台装有INTEL Xeon(R)W-2225 CPU和NVIDIA RTX 2080 Ti的机器上操作,并使用PyTorch实现。此外,在所设计的模型中,L=4,C=512,T=2,Z=3。

2.3 实验结果及其分析

为了验证所提出模型的显著性能,本文比较了两种非学习的配准方法ICP[27]和FGR[28],以及基于学习的配准方法,包括DCP[7]、IDAM[8]、RPMNet[20]、DeepBBS[29]、PREDATOR[30]、RGM[9]、ROPNet[31]和MFGNet[32]。除特殊说明外,所有实验均基于ModelNet40数据集。为了消除数据处理方法和操作设备的影响,本文对所有参与对比的模型均重新训练和测试。

不可见形状 不可见形状表示被测对象的类别在训练中是可见的,但是该对象所具有的形状并没有出现在训练集中。本小节实验中将其分为完整到完整的噪声点云和部分到部分的噪声点云,并分别讨论它们的性能。完整点云意味着每个点云都被均匀采样1 024个点来表示对象的完整轮廓。为了模拟部分到部分的配准,实验中按照RPMNet的方式分别从两个完整点云中删除30%的点。表1和表2分别展示了上述设置下的实验结果。可见,本文的方法在6个评估指标中均取得了出色的表现。同时也说明了所构建的模型在形状不可见的情况下,无论是针对完整点云还是部分点云,都是有效的。

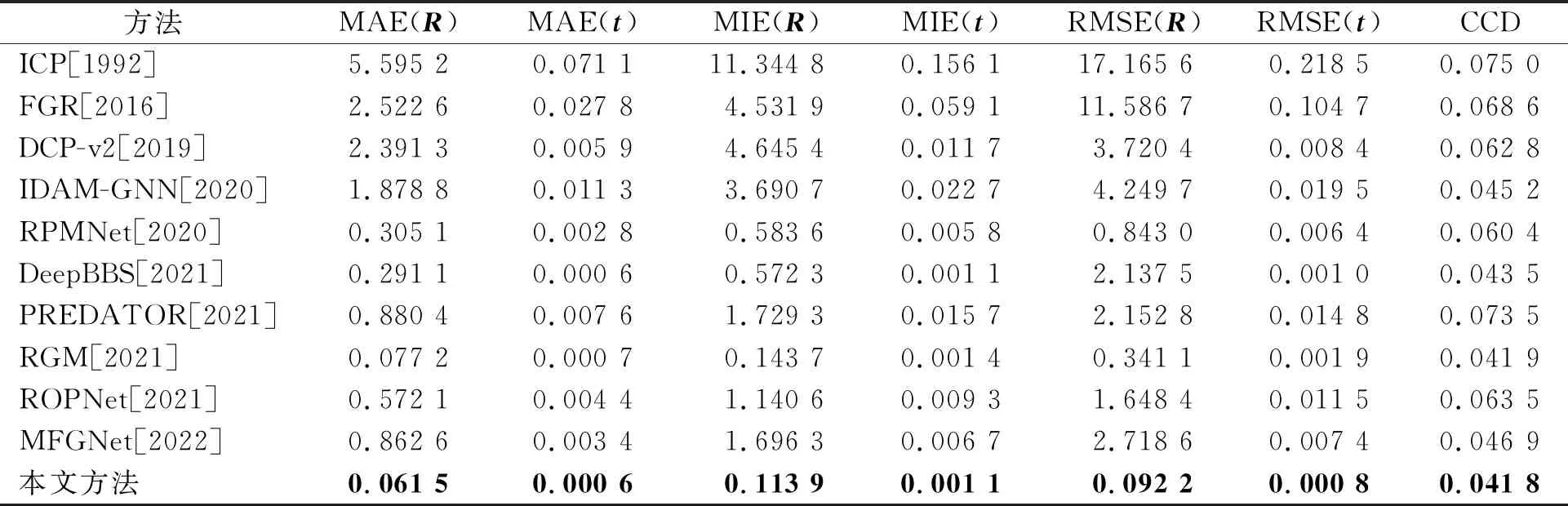
表1 完整到完整的噪声点云在不可见形状上的定量比较

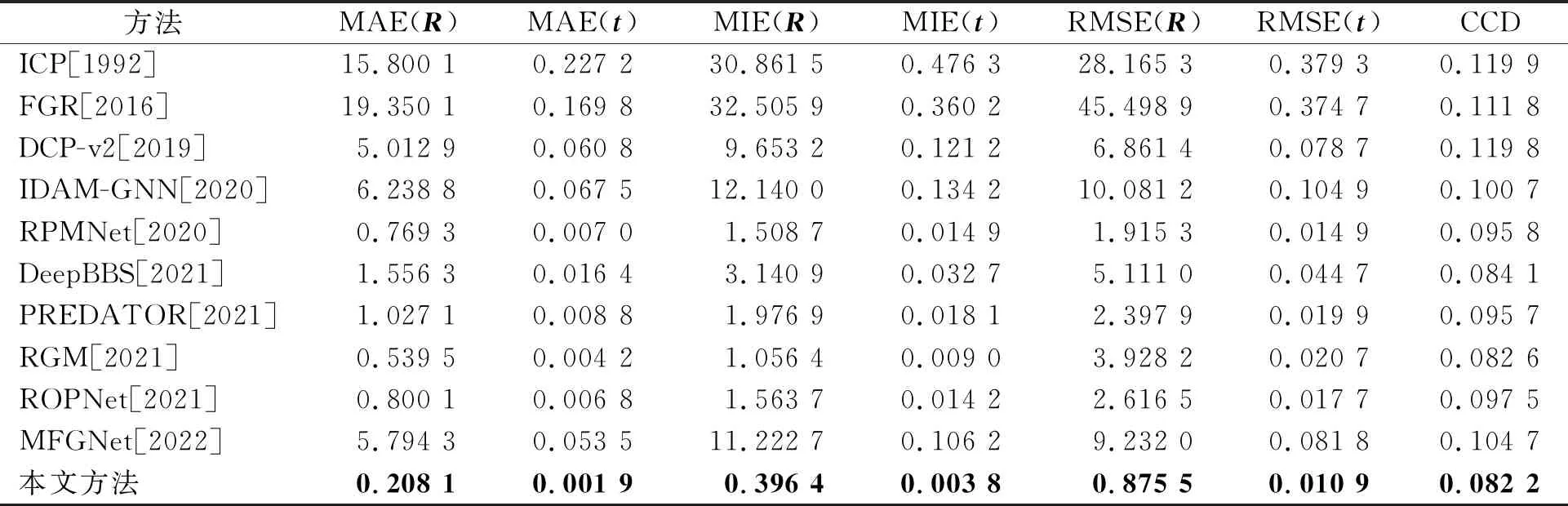
表2 局部到局部的噪声点云在不可见形状上的定量比较

不可见类别 为了进一步揭示所提出方法的有效性,本文所构建的模型和所有的对比方法都在前20个类别上进行训练,并在剩余20个类别上进行测试。从表3和表4所展示的结果可以看出,本文构建的模型在未知类别上的泛化性能具有很强的优越性。从侧面看,构建的基于自适应局域投票的图卷积通过关注局部结构中高级代理点之间的关系,可以有效地捕捉到每个节点的判别性信息。此外,图5展示了完整到完整点云配准的可视化结果,图6展示了局部到局部点云配准的可视化结果,从中可以观察到本文模型能够实现较好的视觉效果。

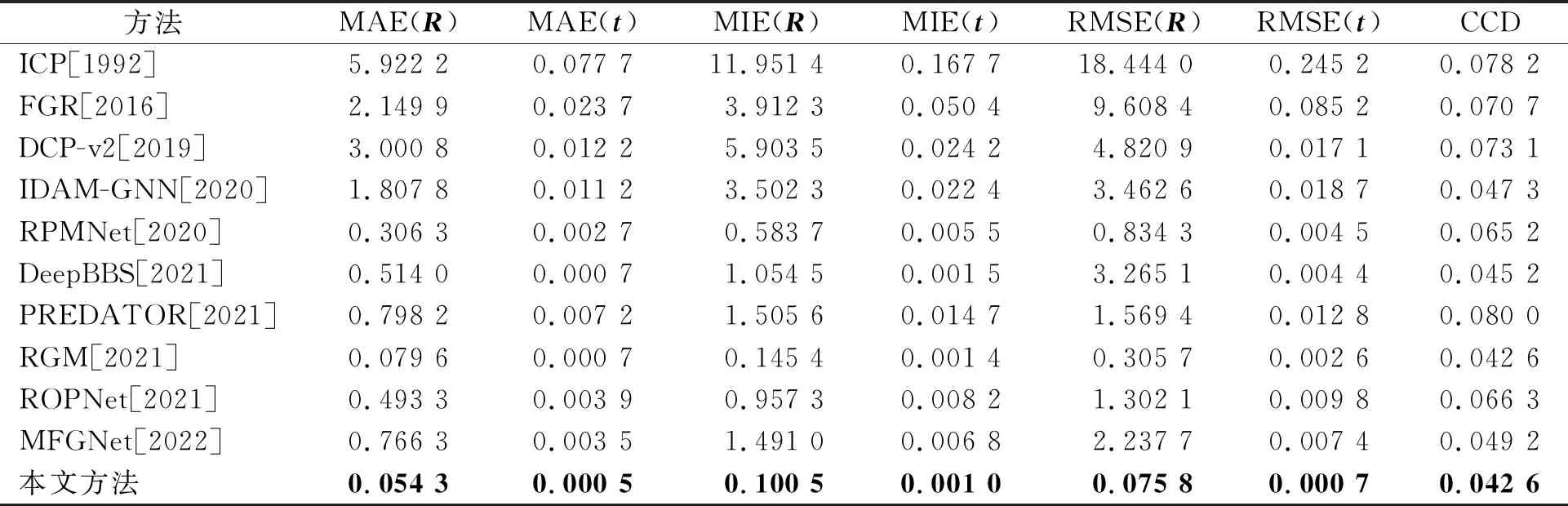
表3 完整到完整的噪声点云在不可见类别上的定量比较

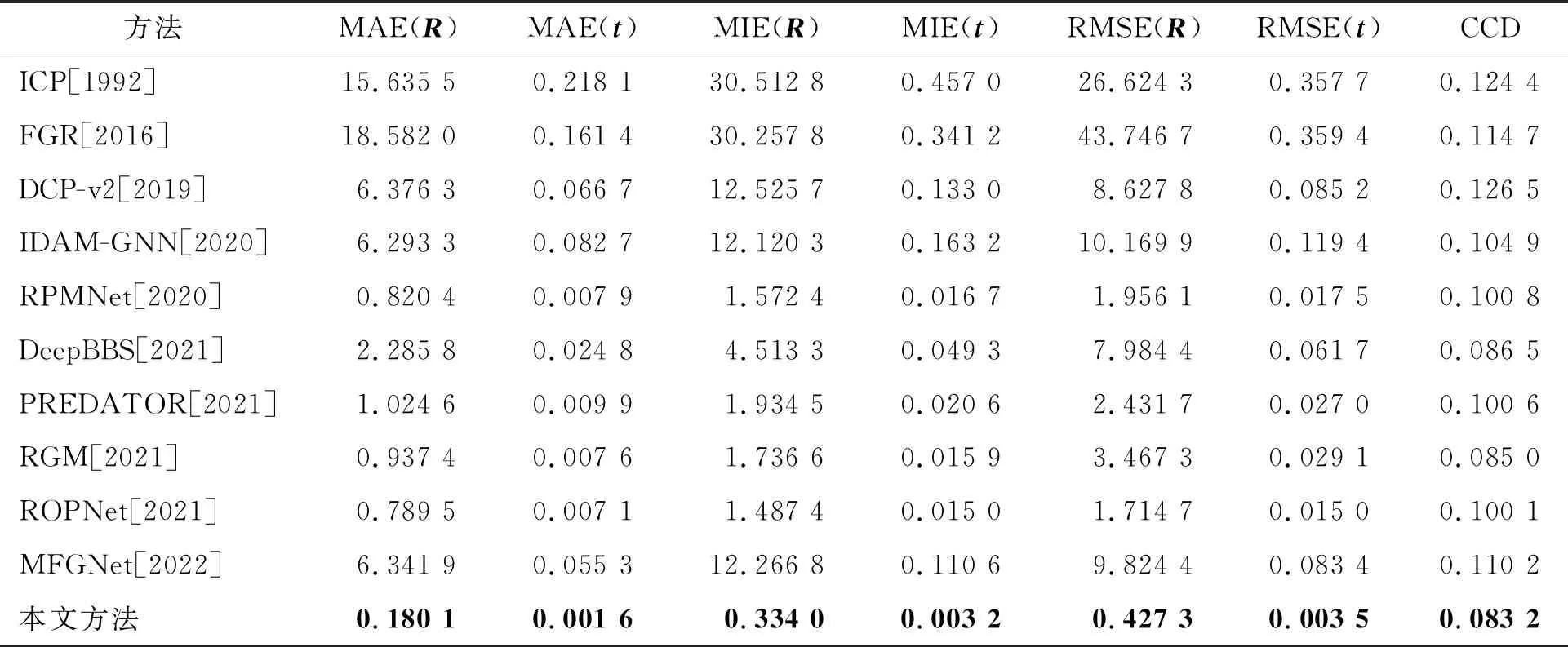
表4 局部到局部的噪声点云在不可见类别上的定量比较

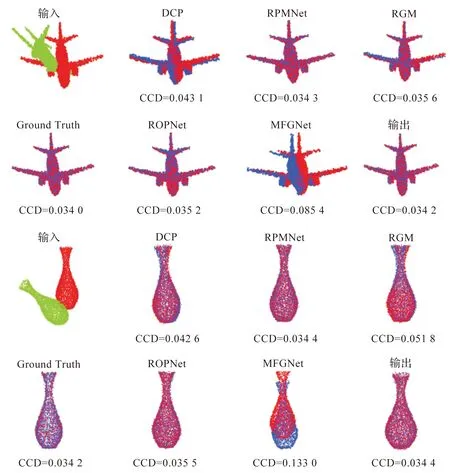
图5 在ModelNet40数据集上的完整到完整点云配准的可视化Figure 5 Visualization of complete-to-complete point cloud registration on the modelnet40 dataset

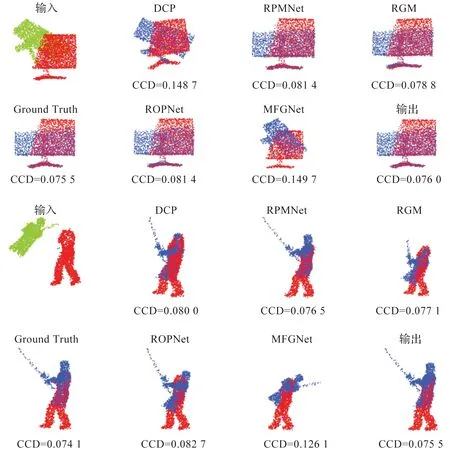
图6 在ModelNet40数据集上的局部到局部点云配准的可视化Figure 6 Visualization of partial-to-partial point cloud registration on the modelnet40 dataset

2.4 消融实验

关键组件的有效性消融实验针对提出的两个重要模块:一是双分支融合学习模块,另一个是二次图结构优化模块。本小节充分讨论了这两个模块对于基础网络的改进效果,测试结果如表5。基础网络(baseline,BL):使用DGCNN作为特征提取网络,并删去二次图结构优化模块。“BL+DBFL”表示将基础模块中的特征提取方式替换成本文构建的双分支融合学习模块,“BL+QGSO”表示在基础网络上增加设计的二次图结构优化(quadratic graph structure optimization,QGSO)模块。表5展示了不同关键组件的消融实验结果,从中可以发现,本文设计的两个模块均使得基础网络的性能得到了不同程度的提升。

表5 所设计模型中不同组成部分的实验效果

2.5 超参数讨论

关于局部图中邻居点数的讨论在使用k-NN构建局部图的过程中,调整邻居点的数量可能产生不同的实验结果。这一部分将详细讨论最近邻居的数量k。超参数讨论的实验依然采用与表4相同的实验设置。具体来说,本小节讨论了k值为10、20和30的情况,并在表6中展示了它们的实验性能。显然,当k=20时评估结果是最优的。因此,本文在实验中将邻居数k固定为20。

表6 特征提取中不同的邻居点数的探讨

2.6 鲁棒性分析

对于训练好的模型,在一定条件下,对不同噪声的容忍性是不确定的。在这一部分中,利用表4中的模型对不同高斯噪声下的配准性能进行预测。高斯噪声分别从分布N(0,0.002)、N(0,0.0052)、N(0,0.012)、N(0,0.0152)、N(0,0.022)中进行采样。从噪声的角度来看,随着噪声的增大,源点云和目标点云的形状将会发生变形,导致两者之间的差异过大而无法识别。同时,这也能增加模型学习对应关系的难度。图7为上述设置下的配准性能预测结果。可以看到,本文设计的模型在平均各向同性误差上取得了出色的结果。总体而言,在一定噪声水平内,本文模型具有抵抗不同等级高斯噪声的能力。

图7 不同噪声等级下模型的抗噪性能Figure 7 Anti-noise performance of the model under different noise levels

2.7 泛化性能

模型在未知的数据上的泛化是深度学习任务应该考虑的问题。为了说明本文设计的网络在未知数据上确实具有良好的泛化性能,本小节同样使用表4中的模型在未知的ShapeNet Parts[33]数据集和现实点云数据集ScanObjectNN[34]上进行测试。ShapeNet Parts数据集包含16个类别,共计16 881个形状。ScanObjectNN数据集包含15 000个对象,这些对象分为15个类,在现实世界中有2 902个对应的对象实例。实验中均采用与ModelNet40相同的设置。从表7和表8中可以看出,本文的模型在ShapeNet Parts和ScanObjectNN上均取得了最好的测试性能,这同时也说明了所构建的模型确实具有良好的泛化能力。

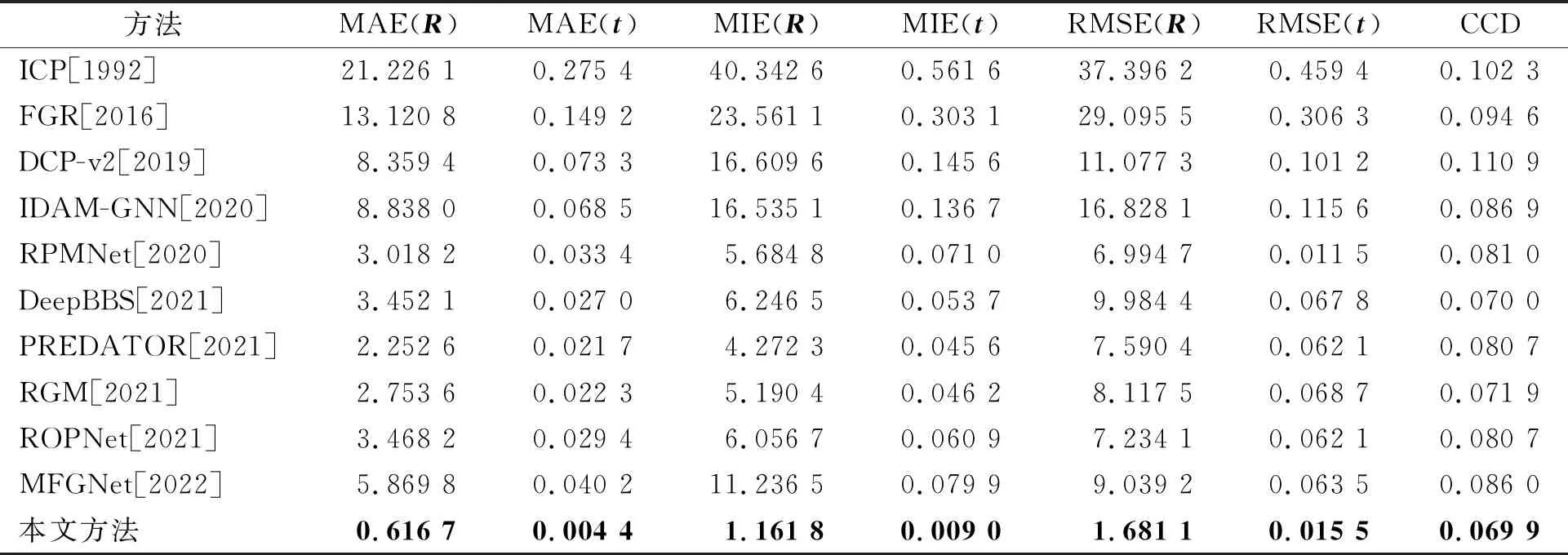
表8 在未知的现实点云数据集ScanObjectNN上的测试性能

3 结 论

在点云配准方面,对于非结构化的点云数据,目前还没有明确且有效地构建邻接矩阵并利用图神经网络进行特征挖掘的工作。因此,本文以此为出发点,明确地构建图结构并采用GCN来有效地抽取判别性的节点特征。具体地,本文通过自适应局域投票的方式动态地学习邻接矩阵并将通过GCN后的特征与经多层感知机获得的特征进行融合,形成双分支融合学习模块,从而减少先前信息的丢失以及减缓GCN所具有的结构平滑现象,这为后续的特征匹配阶段提供了良好的判别性特征。此外,为了缓解深度GCN造成的匹配模糊以及获得节点间正确的对应关系,本文采用了一种针对对应矩阵的二次约束技术,利用Frank-Wolfe算法逐步缩小两个图结构之间的点对特征差异,以达到细化对应矩阵并实现更好的配准性能之目的。从消融实验中可以看出,本文所设计的特征提取方法以及对应矩阵细化方法均能够提高点云配准的性能。本文的方法仍有改进的空间,例如,为对应矩阵设计更加适当且有效的优化方案。此外,由于时间成本和设备问题,还需要考虑和设计轻量级框架来解决大型场景中的点云配准问题。