考虑范德华力的微型活齿传动系统应力分析

曹富林 史旭飞 许立忠

燕山大学机械工程学院，秦皇岛，066004

0 引言

微加工技术的发展(如光刻、电铸和注塑(LIGA)等三维微加工技术逐渐成熟)促进了基于微机电系统(MEMS)技术的微型电机、微型涡轮等微型旋转机械的发展，为微结构中各种能量之间的转换、微动力输出以及大幅度位移运动的实现提供了可能。1988年，FAN等[1]利用微加工技术研制出了直径仅100 μm左右的硅微机械马达(以静电力作为驱动力)，该马达的问世标志着微机电时代的开始。微传动结构是微驱动器核心部件，微驱动器在微机器人、航空航天以及生物医学领域均具有广阔的应用前景。2012年，KAGAN等[2]成功制造出以钛、镍、金为材料的管状微型发动机，其外径为40 μm，并以脉冲超声波为驱动力实现了对发动机的驱动。2013年，GARCA等[3]研制出以催化聚合物、镍、钛为材料的微管发动机，可通过磁场引导输送分子进行细胞免疫测定。2014年，MHANNA等[4]制成一种镍钛合金螺旋微电机，该电机以电磁动力驱动。2017年，MA等[5]研制出过氧化氢酶驱动的Janus颗粒纳米电动机，其尺度在90 nm以下。TU等[6]利用口腔细胞几何形状的非对称性，制造出一种细胞马达，尺度仅有几十个微米。

活齿传动作为一种结构新颖、传动效率高、结构紧凑的传动机构[7]，其微型化研究具有重要意义。科学界一直把研究的重点放在如何制造、控制和操纵微/纳米执行器，对微执行器的物理特性和力学性能的研究较少[8]。DELRIO等[9]和金凯等[10]的研究表明：当器件的尺寸减小至纳米级别时，范德华力对器件工作性能的影响不能忽略不计。为此，本文提出了考虑范德华力的活齿结构力学模型，通过对微型活齿机构的静力分析、接触应力分析，得到考虑范德华力的活齿受力及接触应力变化规律，并探讨了不同几何参数下范德华力对活齿受力状态的影响。

1 系统结构和传动原理

微型集成活齿传动结构见图1，由波发生器H、活齿架S、中心轮K、活齿G四部分组成。

图1 活齿传动模型示意图Fig.1 Movable tooth transmission model diagram

图1中，机构运转时，波发生器H在驱动力的作用下逆时针转动，波发生器H与活齿G产生径向推力，推动活齿G在活齿架S的径向导槽内移动，活齿G与中心轮K的波齿啮合，反推活齿架S顺时针转动，波发生器H的连续旋转迫使活齿G在活齿架S的导槽内往复移动，使活齿架获得连续的旋转运动，从而带动与活齿架固连的输出轴产生连续旋转，完成运动和动力的传递。取样机的活齿数为3，中心轮的波齿数为4，获得传动比为4的微型集成活齿传动系统，其整体径向尺寸为1 μm，厚度为300 nm。

2 活齿受力分析

根据活齿传动原理可知，活齿是传递运动和动力的主要器件，所以选择活齿作为研究对象。由于尺度效应的影响，在一般活齿传动研究中不考虑的分子间作用力、表面力等成为主导因素，微尺度下器件的重力、惯性力等与几何尺寸成三次方关系的体积力则可以忽略不计，上述因素使得微型活齿传动系统的力学模型建立和分析方法不能照搬宏观活齿传动的研究方法，必须结合微型活齿传动自身的特点，建立新的力学模型，提出新的分析方法。对于MEMS结构，随着各器件之间间距的减小，微观作用力逐渐增大，其中范德华力的增长速度最快[11]。为确保活齿的受力分析更为精确，本文将范德华力考虑在内。根据活齿传动系统运动的对称性，可以分析任一活齿在一个啮合周期的受力来代替其余活齿的受力情况，取第j个活齿为研究对象，忽略啮合处摩擦力及活齿重力，将各接触点附近的作用力简化为集中力，啮合副受力分析如图2所示。图2中，FVHj表示波发生器H对活齿G的范德华力，FVSj1、FVSj2分别表示活齿架S齿槽两个侧壁对活齿G的范德华力，FVKj表示中心轮K对活齿G的范德华力；α表示FVKj与Y轴的夹角，β表示FVHj与X轴的夹角，γ表示FVSj1(或FVSj2)与X轴的夹角。

图2 活齿受范德华力示意图Fig.2 Movable teeth by van der Waals diagram

建立与活齿架S固连的固定坐标系Oxy，以中心轮K的几何中心O为坐标原点，它的齿间对称轴为y轴。以活齿中心O2为原点，建立坐标系O2XY。由图2可知，活齿在往复直线运动过程中球心的向径OO2长度为

(1)

得到的活齿内端包络的曲线即为中心轮的实际轮廓线，曲线方程为

(2)

式中,a为波发生器偏心距；r为活齿半径；R为波发生器半径；b=R+r；φ2为中心轮转角；zK为中心轮齿数；0≤α≤π。

由于活齿G的半径相对于波发生器H、中心轮K的曲率半径较小，且考虑到弹性体受力后在接触点附近发生弹性形变，为简化问题，在接触点附近将中心轮外缘与波发生器内缘近似认为是平面。根据文献[12]可知，通常范德华力的作用范围仅为几十个纳米，距离较大时可忽略不计。因在接触点附近波发生器、活齿架、中心轮的尺寸远大于范德华力的作用范围，故将其处理为半无穷体。假定活齿与中心轮、活齿架、波发生器之间仅存在吸引力，对于间距为r0的两分子，根据范德华力场的势函数可得两分子间势能[13]：

(3)

式中，C为分子间相互作用系数。

如图3左图所示，假定活齿上单分子与波发生器内壁的距离为Z，波发生器单位体积分子数量密度为ρ2，活齿球单位体积分子数量密度为ρ1，则活齿上单分子与厚度为dy、宽度为dx的环形微元的势能为[14]

(4)

则该分子与波发生器之间的势能为

(5)

如图3右图所示，为求解活齿与波发生器之间的分子势能，采用微元法，该微元横截面与波发生器的分子势能为

(6)

图3 分子、球面-平面相互作用示意图Fig.3 Molecular, spherical-plane interaction diagram

在活齿运动过程中，活齿与波发生器内壁是接触的，通常假定活齿面距离内壁的距离为d(分子间最小距离)，文献[15]给出其大小0.4 nm，那么沿活齿球水平径向积分，可得到活齿与波发生器之间的分子势能:

(7)

对范德华势函数求偏导，可得范德华力大小：

(8)

A=π2ρ1ρ2C

式中，A为Hamacker常数，是相互吸引力的势能系数。

当d≪r0时，可推导出：

(9)

同理可得

(10)

图4所示为综合考虑范德华力与弹性力时的力学模型。其中，FEKj为中心轮K对活齿G的弹性作用力；FEHj为波发生器H对活齿G的弹性作用力；FESj为活齿架S对活齿G的弹性作用力。

在ΔOO1O2中，由正弦定理知：

(11)

活齿架顺时针转过φ2时，以第j个活齿为研究对象，得到静力平衡方程：

(12)

令

FHj=FEHj-FVHj
FSj=FESj+FVSj1-FVSj2
FKj=FEKj-FVKj

求解上述静力平衡方程，得

(13)

假定参加工作的每个活齿在活齿架内无间隙移动，在驱动力的作用下，波发生器与活齿接触产生弹性形变，当波发生器转过一个小角度Δθ时，活齿在接触位置产生的弹性形变呈正弦规律变化[16]：

(14)

式中,δi为活齿在不同位置的弹性变形量；δmax为活齿弹性变形量的最大值。

可近似认为活齿的变形量与活齿受到的接触力成正比，即可推得[17]

(15)

式中，Fjmax为波发生器对单个活齿的最大作用力。

当负载转矩为Te时，根据扭矩平衡，活齿架承受的扭矩TeS=Te。活齿架受到的转矩与参与啮合的n个活齿产生的力矩相平衡，则可以推知：

(16)

(17)

将式(14)、式(15)、式(17)代入式(16)，可得

(18)

令

联立式(13)、式(15)、式(18)，则有：

(19)

则活齿受到弹性力的大小为

(20)

3 活齿的接触应力分析

假设活齿传动各零件均为均匀的、各向同性的完全弹性体，且接触面为理想的光滑表面。接触区发生小变形，则可根据Hertz弹性接触理论，对活齿的接触应力进行分析计算。

取受载前两弹性体公切面为xy平面，Z轴正向为过接触点O的弹性体内法线方向，如图5所示，两弹性体在点O附近的曲面方程分别为z1=f1(x,y)，z2=f2(x,y)。由于接触面尺寸与弹性体曲率半径相比尺寸很小，故略去高阶项，可用下面的表达式近似表示原点附近的曲面：

(21)

则点O附近弹性体表面上两点S1和S2的距离为

z1+z2=(A1+A2)x2+(B1+B2)y2+
(C1+C2)xy

(22)

图5 接触数学模型示意图Fig.5 Contact mathematical model diagram

通过坐标变换使得xy项的系数为零，则有：

z1+z2=Ax2+By2

(23)

式中，x、y为S1、S2两点在新坐标系下的坐标。

假定在接触点O处，弹性体1的主曲率半径为R11、R12，弹性体2的主曲率为R21、R22，两个表面的主曲率轴的交角为θ，根据光滑非协调表面接触特性，得

(24)

在压缩过程中，两弹性体内部远处的点分别向O点平行于Z轴方向移动位移δ1、δ2，若接触时不发生形变，则它们的轮廓如图5虚线所示，两弹性体表面由于接触力发生平行于Z轴的位移，其位移大小为w1、w2。若发生形变后S1和S2点在接触面内重合，则有：

w1+w2=δ1+δ2-(z1+z2)

(25)

如果接触的两个弹性体均为旋转体，于是弹性体接触区为半径为c的圆[18]，且有R11=R12=R1，R21=R22=R2，于是得

(26)

联立式(23)、式(25)、式(26)，可得在接触区内有：

(27)

式中，R0为接触区内任意点到接触中心的距离。

作用于两个相互接触无摩擦弹性旋转体之间的应力分布由Hertz理论给出：

(28)

式中，pmax为接触区圆心处的应力最大值。

由于作用于弹性体1的力与作用在弹性体2上的力相等，故根据弹性力学得到接触区内的位移为

(29)

式中，ν1、ν2分别为弹性体1和2的泊松比；E1、E2分别为弹性体1和2的弹性模量。

联立式(27)、式(29)，可得接触区圆形域的半径：

(30)

作用在弹性体上的力与接触应力的关系为

(31)

联立式(30)、式(31)可得

(32)

因为活齿为旋转体，且活齿曲率半径较小，故将波发生器、活齿架和中心轮与活齿接触点的附近近似处理为平面。令R1→r，R2→∞，可得活齿受到的接触应力峰值为

(33)

将波发生器、活齿架和中心轮对活齿的作用力FEHj、FESj和FEKj代入式(33)，可得对应的接触应力:

(34)

4 算例的求解与分析

4.1 活齿受力算例

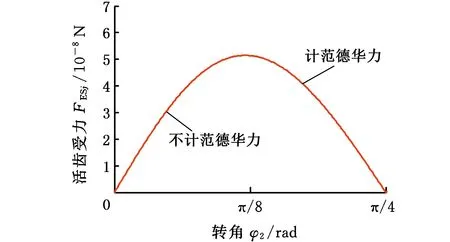
选择波发生器H的半径R=400 nm，偏心距a=20 nm，活齿半径r=50 nm，活齿齿数ZG=3，中心轮波齿数ZK=4，阻力矩Te=10-14N·m，Hamacker常数A=4×10-19J，根据式(19)、式(20)，可得到范德华力对活齿受力的影响，如图6所示。

由图6可知，啮合活齿在活齿架导槽内移动过程中，范德华力对活齿架的作用力变化无影响。当只考虑弹性力且活齿处于啮入啮出位置时，受到的作用力FEHj、FESj和FEKj均为零，随着活齿在齿槽内移动，作用力缓慢增加，在中心轮转角为π/8时出现受力峰值，当中心轮转角为π/4时，活齿啮出，完成一个工作循环。考虑范德华力时，活齿开始啮入与啮出时，受力均不为零，且波发生器和中心轮对活齿的弹性作用力均增加1.17倍左右。据此可知，范德华力在微尺度下对活齿的受力具有显著影响，不可忽略。

4.2 活齿应力算例

表1给出了微型活齿传动系统中活齿、波发生器、活齿架以及中心轮的材料类型以及材料的弹性模量、泊松比。纳米材料具有大的比表面积、高浓度晶界，这对纳米材料的物理及力学等性能有着重要影响，纳米镍许用强度为5～7 GPa，纳米氮化硅抗压强度最高可达15 GPa，纳米聚甲基丙烯酸甲酯的抗压强度为700～1 000 MPa。

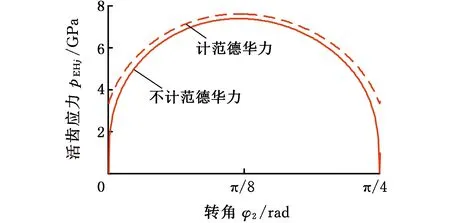
将表1中的数据代入式(34)，可得考虑范德华力时任意活齿在一个工作循环内的接触应力变化，见图7。啮合活齿在活齿架齿槽中一个工作周期内的接触应力变化规律与啮合活齿的受力变化规律相同，范德华力对活齿架作用下的接触应力无影响；对于波发生器与中心轮，在考虑范德华力的情况下，活齿啮入点和啮出点存在较大的接触应力突变，且活齿受到的接触应力增大了30 MPa，范德华力对接触应力影响显著。

(a)波发生器

(b)活齿架

(c)中心轮图6 考虑范德华力时活齿受力对比图Fig.6 Consider Van der Waals force movable toothforce comparison chart

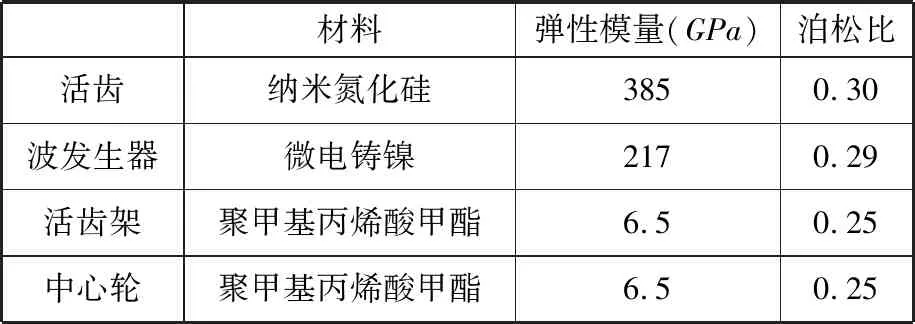
材料弹性模量(GPa)泊松比活齿纳米氮化硅3850.30波发生器微电铸镍2170.29活齿架聚甲基丙烯酸甲酯6.50.25中心轮聚甲基丙烯酸甲酯6.50.25

(a)波发生器

(b)活齿架

(c)中心轮图7 考虑范德华力时活齿接触应力对比图Fig.7 Consider van der Waals force movable toothcontact stress comparison chart

5 参数变化对活齿受范德华力的影响

以任一活齿为例，改变活齿传动结构的几何参数，得到范德华力对活齿受力规律变化的影响，如图8～图10所示。

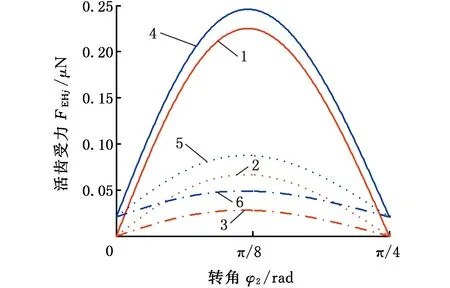
(1)分析图8可知，随着波发生器偏心距a的增大，范德华力的大小不变，但范德华力对活齿受到弹性力的影响明显增加。当a增至初值的两倍时，考虑范德华力时，活齿受到的弹性力FEHj、FEKj约为不考虑范德华力时活齿受到弹性力的2倍,活齿受到的接触应力pEKj、pEHj约增大1倍。可见，偏心距a对范德华力产生的作用有明显的影响。

(2)由图9可知，随着活齿半径r的增大，活齿受到的范德华力明显增大，当活齿半径增大80%时，活齿受到的范德华力也增大80%，同时，考虑范德华力时，活齿受到的弹性力FEHj、FEKj约为不考虑范德华力时活齿受到弹性力的1.25倍，活齿受到的接触应力pEKj、pEHj约增大20%。可见，活齿半径r对范德华力产生及范德华力产生的作用均有明显的影响。

(a)波发生器与活齿的作用力

(b)波发生器与活齿的接触应力

(c)中心轮与活齿的作用力

(d)中心轮与活齿的接触应力1.a=20 nm 2.a=30 nm 3.a=40 nm 4.考虑范德华力，a=20 nm 5.考虑范德华力，a=30 nm 6.考虑范德华力，a=40 nm图8 活齿受力随偏心距a的变化Fig.8 Movable tooth with eccentricity a change

(a)波发生器与活齿的作用力

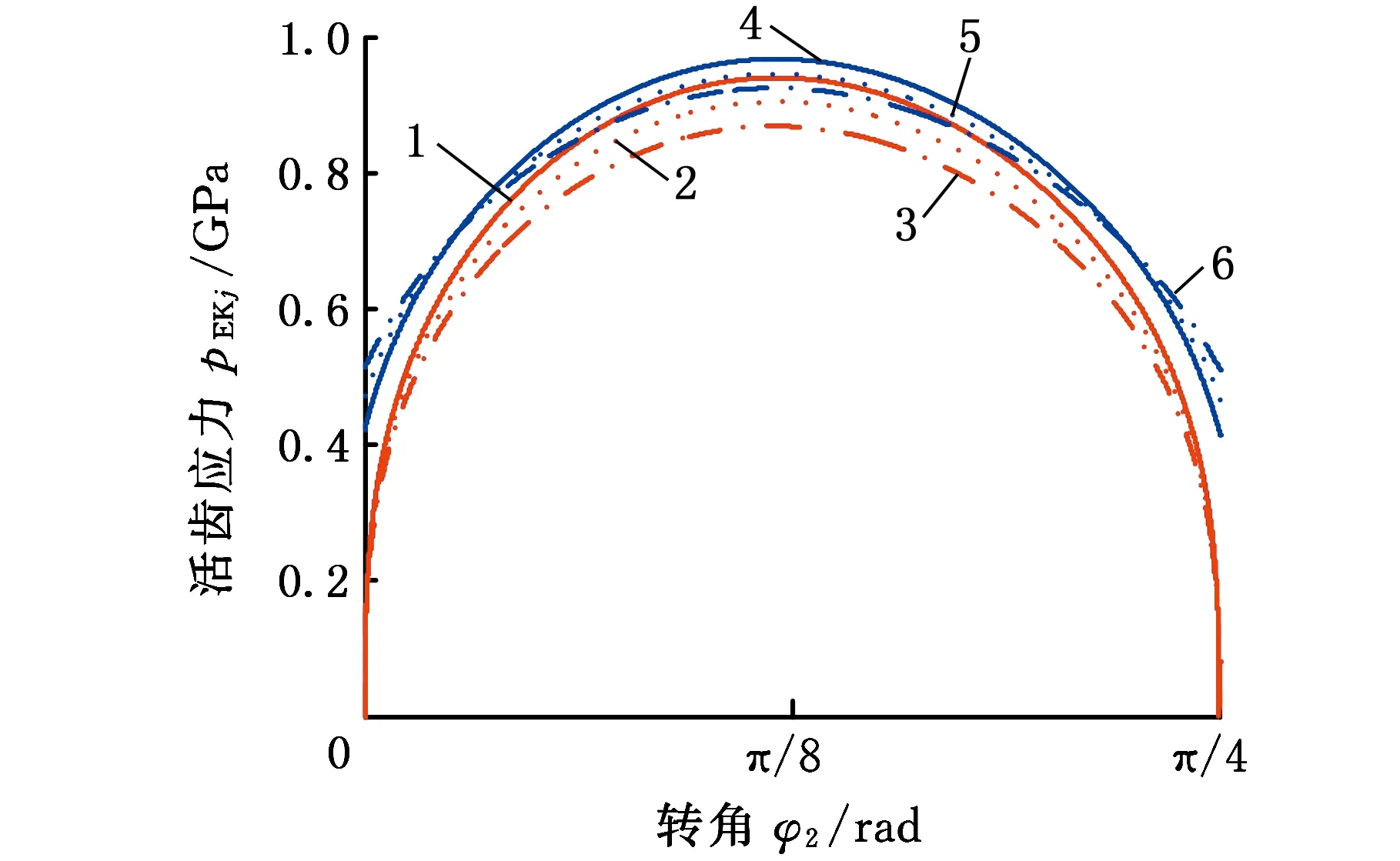
(d)中心轮与活齿的接触应力1.r=50 nm 2.r=70 nm 3.r=90 nm 4.考虑范德华力，r=50 nm 5.考虑范德华力，r=70 nm 6.考虑范德华力，r=90 nm图9 活齿受力随活齿半径r的变化Fig.9 The force of movable tooth changes with the radius of movable tooth’s r

(a)波发生器与活齿的作用力

(b)波发生器与活齿的接触应力

(c)中心轮与活齿的作用力

(d)中心轮与活齿的接触应力1.R=400 nm 2.R=450 nm 3.R=500 nm 4.考虑范德华力，R=400 nm 5.考虑范德华力，R=450 nm 6.考虑范德华力，R=500 nm图10 活齿受力随波发生器半径R的变化Fig.10 Movable teeth with wave generator changes the force by the radius R

(3)分析图10可知，随着波发生器半径R的增大，范德华力的大小不变，范德华力对活齿受到弹性力的影响减弱，当波发生器半径增大25%，考虑范德华力时，活齿受到的弹性力FEHj、FEKj约为不考虑范德华力时活齿受到弹性力的1.1倍，活齿受到的接触应力pEKj、pEHj约增大7%。可见，波发生器半径R对范德华力产生的作用较弱。

综上所述，在考虑范德华力的情况下，波发生器偏心距、活齿半径、波发生器半径等几何参数均对活齿受到的作用力及接触应力有不同程度影响，其中活齿半径、波发生器偏心距和范德华力的影响正相关，且波发生器偏心距影响较大；波发生器半径对范德华力的影响较弱。

6 结论

根据半无穷空间理论，应用范德华势函数，推导出活齿受范德华力的公式，在考虑范德华力的情况下，建立了任一活齿不同啮合位置处的静力学方程，并得到波发生器、活齿架、中心轮对活齿的作用力与转角的关系式，得出了微尺度下活齿受力变化曲线；同时运用接触力学理论，得到了在考虑系统不同几何参数设置情况下啮合活齿在波发生器、中心轮作用下活齿接触应力的变化规律曲线，并分析了不同情况下范德华力的影响强弱。