多浮体原油转驳系统在南海海域卸载作业过程中的稳定性分析

蔡舒鹏, 张永康*, 池元清, 宋 健, 谭桂斌, 黄 兴, 李 荣, 吴承恩, 万家平, 蔡 灵, 高 航, 王宣平, 庄瑞民, 赵勇平

(1. 广东工业大学 机电工程学院, 广东 广州 510006;2. 启东中远海运海洋工程有限公司, 江苏 南通 226200;3. 大连理工大学, 辽宁 大连 116024;4. 广东中远海运重工有限公司, 广东 广州 510700)

0 引 言

目前，全球有100多艘浮式生产储卸油装置(Floating Production Storage and Offloading，FPSO)投入使用，已成为海洋石油开采设备的主力军[1]。作为FPSO卸油系统的重要组成部分，原油输送设备的需求量正在迅猛增长[2]。在通常情况下，FPSO卸油任务由穿梭油船完成。然而，穿梭油船的运行和维护成本远高于同吨位的常规油船。穿梭油船的载重量为8万～15万t，而常规油船的载重量为30万～40万t[3]。因此，在开发大型、长距离、深海油气资源时，如果能充分利用常规油船成本效益高、载重能力大的优势，将会显著提高生产效率、降低生产成本[4]。基于上述背景，近年来提出使用深海动力定位原油转驳船(Crude Transfer Vessel，CTV)替代穿梭油船进行原油转驳的新方法[5]。图1为一艘由广东中远海运重工有限公司建造并于2020年交付船舶所有人使用的深海远洋原油转驳船，其配备动力定位(Dynamic Positioning，DP)系统。与此同时，还引入一种“FPSO+CTV+VLCC(超大型原油运输船)”的原油转驳卸载作业新模式。

图1 广东中远海运重工有限公司已交付的Sealoader 2

在此模式下，CTV利用其DP装置的全方位推进功能拉动常规油船(如VLCC)相对于FPSO进行系泊定位，通过使用大口径油管，FPSO中的原油先输送至CTV，然后CTV将原油卸载至常规油船。这种原油运输方式是一种国际性的创新，因其成本低、安全、灵活而越来越受到欢迎。

在常规油船的装载阶段，CTV的DP系统使其可在常规油船作业环境定位后围绕FPSO作业区旋转，同时将常规油船保持在作业区内，而使常规油船在相对位置保持平衡的回拉力由额外配置的拖船提供。因此，与传统海上船舶相比，CTV的原油卸载操作更复杂，因为其包含多浮体(CTV、油船和拖船)的耦合动态稳定性。

国内外许多研究人员对海洋浮体的动态定位进行分析。鲍威尔[6]研究DP系统的时域分析。TANNURI等[7]在DP系统上进行试验，应用一个扩展的卡尔曼滤波器配合比例微分控制器研究推进器的最优分配算法。赵伟[8]研究DP系统的推力器分配算法。XIN等[9]研究考虑未知时变海洋扰动时DP系统的控制方法。LEE等[10]研究海洋船舶非线性纵摇运动的综合控制性能，证明抑制横摇和纵摇运动的影响对于提高船舶的机动性和稳定性至关重要。HU等[11]和胡开业等[12]分析CTV的DP系统在设计海况下的性能要求，然后研究其相应的作业模式，并提出一种最小化推进器功率和作用力的算法。GAIDAI等[13]采用平均条件超越率(Average Conditional Exceedance Rate，ACER)方法和蒙特卡罗法产生多组随机风速载荷样本，研究渤海湾卸载作业期间FPSO船舶的极限缆索张力。TANNURI等[14]对巴西油田的CTV卸载操作进行全面的数值分析。

在上述工作的基础上，本文主要研究多浮体系统(CTV、油船和拖船)在南海海域进行原油卸载作业时的稳定性。根据船舶的定位和拖曳模式，考虑多浮体系统所受的复杂环境载荷(包括风载荷、海流载荷和波浪载荷)，将从AQWA水动力分析得到的结果输入MATLAB中进行初始条件的预设，用fsolve函数求解非线性方程组，研究原油卸载过程中多浮体系统在不同环境条件下可能保持准静态平衡的位置；利用fmincon函数求解多约束单目标非线性优化问题，得出保持准静态平衡时CTV推进器所需的最小推进力。研究结果将为使用附带DP系统的CTV和“FPSO+CTV+VLCC”原油转驳卸载作业新模式开发南海深海油气资源及相关项目提供理论参考。

1 CTV卸载模式

在实际作业中，FPSO由多点系泊系统固定，其位置和方向不会随外载荷的改变而变化，而CTV和常规油船的方位则取决于风浪流的方向。在卸载作业模式中，CTV拖曳由CTV、常规油船和拖船组成的多浮体系统，在FPSO的系泊点接近并开始输送原油，在卸载作业模式中CTV相对于FPSO的可能位置如图2所示[14]，区域(1)代表安全工作区域，区域(2)代表警示区域，区域(3)代表危险作业区(图2工况下的安全工作区域回转角度为239°)。由于受到不断变化的风载荷、波浪载荷和流载荷的影响，CTV需要不断调整其DP系统以控制本身作业区域的位置，并保持多浮体系统的相对平衡位置，以避免发生碰撞并保证原油转驳的顺利进行，因此研究卸载系统在复杂变化水文环境中的稳定性至关重要。

图2 FPSO船尾卸载站工作区示例

在通常情况下，CTV所受的环境载荷主要会对船体的纵荡、横荡和艏摇造成影响，而对另外的垂荡、纵摇和横摇等3个方向的影响可忽略不计，因此其在计算中不包含在内，动力定位DP系统主要由主推进器、方向舵、方位推进器和隧道推进器控制其动态平衡，CTV所受的环境载荷和动力载荷如图3所示。为简化问题，不考虑船体所受阻尼，只考虑船体所受载荷及自身提供的推进力。

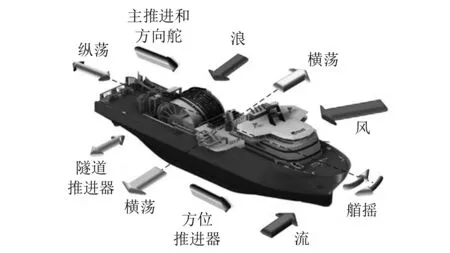
图3 CTV所受环境及动力载荷

2 典型环境载荷

主要针对卸载作业模式中多浮体系统在复杂环境载荷作用下的稳定性进行分析，整个卸载系统的总环境载荷包括风载荷、海流载荷和波浪载荷等3个部分，均随海况变化，不考虑它们之间的耦合效应，根据地理常识，南海海域夏季盛行西南季风，而冬季盛行东北季风。南海在某年夏季的平均环境参数[15]如表1所示。CTV、常规油船和拖船的尺寸参数[14]如表2所示。

表1 南海海域平均环境参数

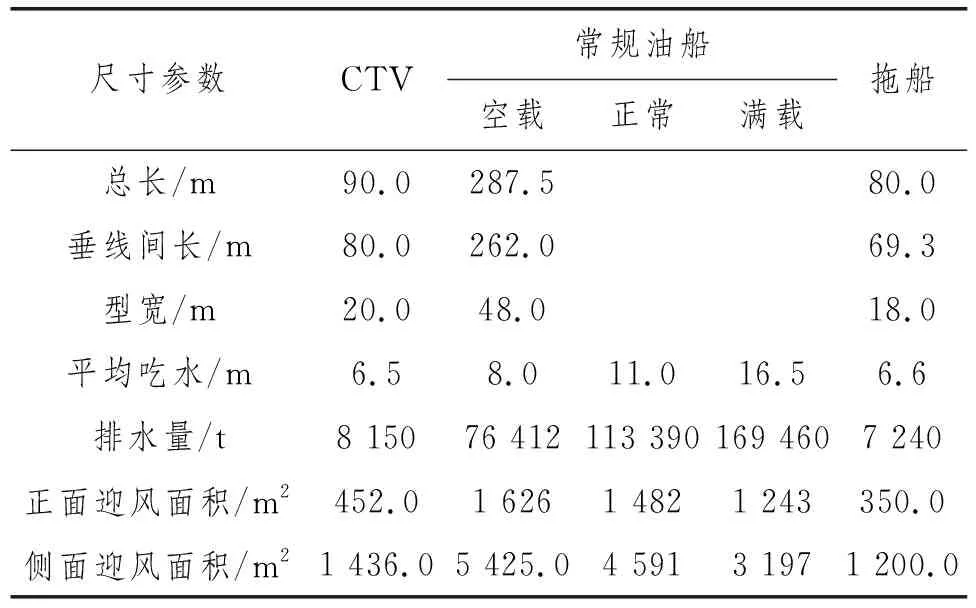
表2 船体尺寸参数

2.1 风载荷

将风载荷看成分布均匀的速度场，根据传统的牵引力公式可得：

(1)

(2)

(3)

式(1)～式(3)中：Fwx、Fwy和Mwφ分别为风载荷在船的纵荡、横荡和艏摇等3个方向的贡献；ρa为空气密度；vw为海平面上10 m的风速；Cwx(φw)、Cwy(φw)和Cwz(φw)分别为风载荷在船的纵荡、横荡和艏摇等3个方向上的系数；φw为风相对于船体x轴正方向的入射角；AF和AL分别为正面和侧面迎风面积；L为船总长。

2.2 流载荷

将流载荷速度场看成分布均匀的速度场，则流载荷可表示为

(4)

(5)

(6)

式(4)～式(6)中：Fcx、Fcy和Mcφ分别为流载荷在船的纵荡、横荡和艏摇等3个方向上的贡献；ρc为海水密度；vc为海流的相对速度；Ccx(φc)、Ccy(φc)和Ccz(φc)分别为流载荷在船的纵荡、横荡和艏摇等3个方向上的系数；φc为海流相对于船体x轴正方向的入射角；T为船的平均吃水深度。

2.3 波浪载荷

船在纵荡方向上的平均波浪力计算式为

(7)

式中：S(ω)为频率为ω的波谱；Dx为纵荡方向的漂移系数；β0为波浪相对于船体的载荷。对于波浪载荷在横荡和艏摇方向上的载荷Fwvy和Mwvφ，其公式与纵荡方向相似。根据谱分析法可计算出3艘船的二阶波浪载荷。

3 多浮体系统在原油卸载过程中的稳定性分析

为分析由FPSO-CTV-常规油船-拖船组成的多浮体系统在原油卸载过程中稳定性，建立相应坐标系(见图4和图5)，规定指向船首方向为0°，指向船左舷方向为90°，船体局部坐标系为xoy，全局坐标系为XOY，船体与全局坐标系夹角为φ，船首转动角为M。由于FPSO是多点系泊固定，其位置和方向不会随外载荷的改变而变化，因此原油卸载过程中的多浮体系统可简化为由CTV-常规油船-拖船组成的三浮体系统。在船体俯视水平面上建立一个NED(North East Down)坐标系，即北东地坐标系(北轴指向地球北，东轴指向地球东，地轴垂直于地球表面并指向下)，如图6所示。假设：CTV、常规油船和拖船的船头与正北方向的夹角分别为φ1、φ2和φ3；CTV、常规油船和拖船的船总长分别为L1、L2和L3；连接CTV与常规油船的缆绳的绳子张力为T1，连接常规油船与拖船的缆绳的绳子张力为T2；缆绳与CTV船尾的夹角为α1，与常规油船船首夹角为θ1；缆绳与常规油船船尾夹角为α2，与拖船船首夹角为θ2；拖船推进器的推进力由F3表示，与拖船船尾的夹角为α3。

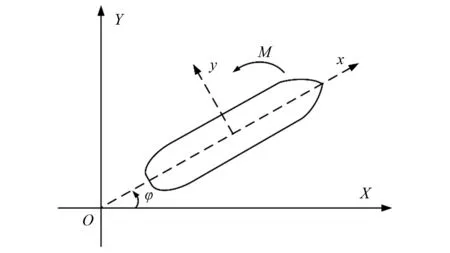
图4 船体所受载荷俯视水平面及对应坐标系

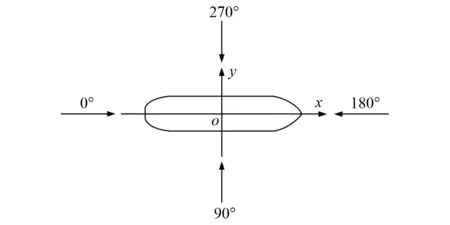
图5 根据船体所构建的坐标系和入射角

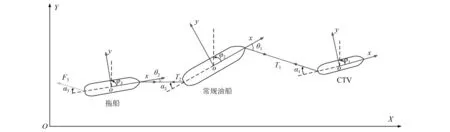
图6 原油卸载过程中的三浮体系统水平示例

3.1 三浮体系统的准静态平衡位置

在原油卸载过程中，CTV控制自己的DP系统使其围绕FPSO作业区旋转，保持与常规油船对齐以便进行原油转驳。油船的航向取决于其所受环境载荷、连接拖船的缆绳所施加的回拉力和连接CTV的缆绳施加的动态定位力，因此需要先分析常规油船-拖船子系统(见图7)，以确定常规油船船首航向。

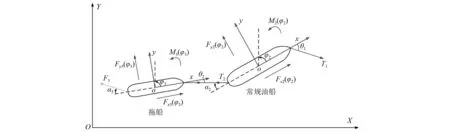
图7 常规油船-拖船子系统所受环境载荷及外力

设常规油船在纵荡、横荡和艏摇等3个方向上所受的环境载荷分别为Fx2(φ2)、Fy2(φ2)和M2(φ2)，拖船在纵荡、横荡和艏摇等3个方向上所受的环境载荷分别为Fx3(φ3)、Fy3(φ3)和M3(φ3)。环境载荷可由式(1)～式(7)通过ANSYS/AQWA建模计算得出。由图6的几何关系可得：

θ1=φ1-φ2+α1

(8)

θ2=φ2-φ3+α2

(9)

根据图7可写出使常规油船-拖船保持平衡时在纵荡、横荡和艏摇等3个方向上的力平衡方程：

T1cosθ1-T2cosα2+Fx2(φ2)=0

(10)

T2cosθ2-F3cosα3+Fx3(φ3)=0

(11)

-T1sinθ1+T2sinα2+Fy2(φ2)=0

(12)

-T2sinθ2+F3sinα3+Fy3(φ3)=0

(13)

(14)

(15)

由式(10)～式(15)可知，一共有T1、θ1、T2、α2、φ2、F3、φ3和α3等8个未知数，但只有6个可用方程，因此该问题涉及不定非线性方程组的求解，需要固定额外的参数才有可能求解。

由于缆绳必须位于船体的外侧才能保证绳子张力，因此隐含的几何条件为

-90°≤θ1，α2，θ2≤90°

(16)

在实际的原油卸载过程中，拖船推进器的推力可根据常规油船的船头朝向不断调整，因此可固定拖船给予常规油船的拉力F3=196 kN，而α2的取值范围为-90°～90°，这样可将未知数数目降为6个并进行求解。

(17)

(18)

式(17)和式(18)中上标星号代表达到平衡点的解。

稳定性平衡意味着发生微小扰动之后造成的转矩会使系统有马上恢复到原来平衡点的趋势，因此在平衡点附近的导数应为负值，即

(19)

(20)

计算表明，只有少数位置能够同时满足稳定性平衡条件和几何约束条件。

3.2 CTV推进器的推进力

一旦常规油船-拖船子系统保持平衡时的载荷确定，即可联立式(8)～式(15)计算CTV船首航向和DP系统提供的推进力。CTV所受的环境载荷和外力如图8所示，设CTV在纵荡、横荡和艏摇等3个方向所受的环境载荷分别为Fx1(φ1)、Fy1(φ1)和M1(φ1)，DP系统船尾方位推进器推力分别为Fpx1和Fpy1，船首方位推进器推力分别为Fpx2和Fpy2。

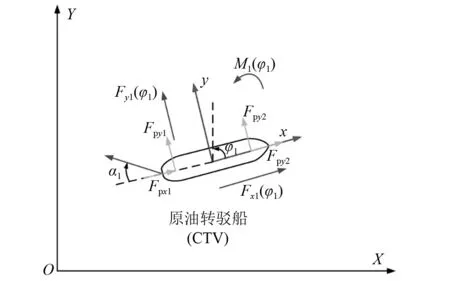
图8 CTV所受环境载荷及外力

CTV保持平衡时的船首航向可由计算其位置的风向标算法得出，在该算法中，需要寻找的船首航向会使船首推进器的横荡推进力Fpx2和Fpy2最小。因此，该问题转化为求解一个多约束的单目标非线性优化问题，其中船首与北向的夹角为决策变量，而优化函数为船首推进器的横荡推进矢量和。第3.1节已求出在拖船拉力F3固定时，其他相关未知变量的可行解T1、θ1和φ2，因此该优化问题可表示为

(21)

Fpy1+Fpy2+Fy1(φ1)+T1sinα1=0

(22)

Fpx1+Fpx2+Fx1(φ1)-T1cosα1=0

(23)

(24)

(25)

(26)

-90°≤φ2+θ1-φ1≤90°

(27)

式(21)～式(27)中：Fsway为总横荡推进力；Fp1max和Fp2max分别为船尾方位推进器的极限推进力。式(27)的最后一项表示缆绳的方向必须指向船体外侧。根据式(8)和式(9)，可将式(22)～式(24)中的未知变量α1代换掉，则未知变量降为5个：φ1、Fpx1、Fpy1、Fpx2和Fpy2。对于每个可能的φ1值，通过求解式(22)～式(24)可能求出一系列满足条件的Fpx1、Fpy1、Fpx2和Fpy2，但其值还需要满足涉及极限推进力的不等式组。该多约束单目标非线性优化问题可通过MATLAB中的fmincon函数使用内点法解出。计算三浮体系统在准静态平衡时的相对位置和CTV推进器推力的流程图如图9所示。

图9 计算流程图

3.3 结果讨论

图10～图12分别显示在南海的不同环境载荷下，原油卸载作业过程中，CTV-常规油船-拖船构成的三浮体系统可能保持平衡的空间位置，其中，圆圈代表船首位置，星号代表船尾位置，常规油船始终位于3条船的中心位置，其船体中心为坐标原点，常规油船船首与CTV船尾通过较短缆绳连接，常规油船船尾与拖船船首通过较长缆绳连接。由图10～图12可知，对于某特定的环境载荷，只有一些特定的平衡位置满足几何约束不等式。

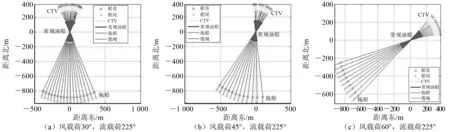
图10 不同风载荷方向下三浮体系统可保持平衡的相对位置比较(风速8.0 m/s)

控制其他参数不变，令风载荷的方向由30°向60°偏转，得到对比图如图10所示：当风载荷方向变化时，对应的可满足准静态平衡的位置向顺时针方向偏转。

控制其他参数不变，令流载荷的方向由210°向245°偏转，得到对比图如图11所示：当流载荷方向变化时，对应的可满足准静态平衡的位置先向顺时针方向偏转再向逆时针方向偏转，这可能是流载荷在该角度区间变化时使风-浪-流耦合载荷的矢量方向发生临界变化，因此其偏转方向也发生相应改变。

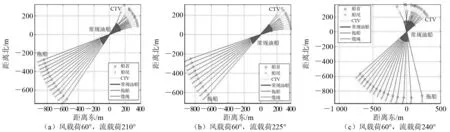
图11 不同流载荷方向下三浮体系统可保持平衡的相对位置比较(风速8.0 m/s)

控制其他参数不变，令风速由6.5 m/s逐渐增大至10.0 m/s，得到对比图如图12所示：随着风速的增大，三浮体系统达到准静态平衡的位置变化较大，在风速从6.5 m/s增加至7.0 m/s的过程中三浮体达到准静态平衡时的排列方式发生彻底变化，而在风速从7.0 m/s增加至10.0 m/s的过程中三浮体的排列方式没有变化，这说明风速的增大也使风-浪-流耦合载荷的矢量方向发生临界变化。由图12(b)～图12(d)可知，在风速从7.0 m/s增加至10.0 m/s的过程中，较大的风速会使可达到准静态平衡的角度区间更窄，这说明在海面上风速较大的情况下，CTV的原油转驳过程会相对困难，要想保证与常规油船之间位置的相对平衡需要DP系统更精确的调整。

图12 不同风速下三浮体系统可保持平衡的相对位置比较(风载荷60°，流载荷225°)

图13给出当环境载荷为表1所示时对应的几何参数。

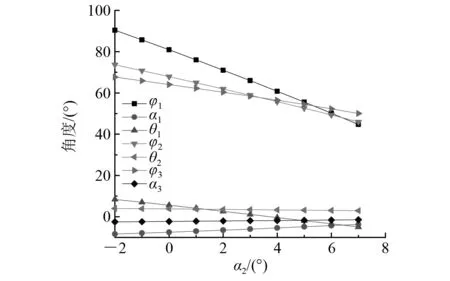
图13 三浮体系统在不同空间位置下的几何角度

由图13可知，船首与正北向夹角φ1、φ2和φ3在该环境载荷作用下较大，而缆绳与船首和船尾的夹角α1、θ1、θ2和α3则保持相对较小的值，在这样的情况下才能保证缆绳中的张力始终保持绷紧且不产生较大艏摇。

图14给出当α2变化时CTV中的推进力和2条缆绳中的拉力变化。

图14 当α2变化时CTV中的推进力和两条缆绳中的拉力变化

由图14可知，2条缆绳中的拉力远大于CTV推进器提供的推力，牵引常规油船船首的缆绳拉力T1大于牵引常规油船船尾的缆绳拉力T2，说明CTV对常规油船的牵引起主要作用，而拖船提供的牵引起辅助稳定作用。CTV在纵荡方向上需要提供的推力远大于在横荡方向上的推力，保持稳定主要靠推进力沿纵荡方向的调整，而横荡方向起辅助作用。

4 结 论

研究由3艘船(CTV、常规油船和拖船)组成的多浮体系统在原油卸载过程中的稳定性。根据船舶的定位和拖曳模式，考虑实际环境载荷，包括风载荷、海流载荷和波浪载荷，计算南海平均环境条件下原油卸载过程中船体可能保持平衡的位置，结果表明：

当船体所受外载荷一定时，三浮体系统只有少数相对位置才能够保持稳定性平衡，控制其他参数不变，当风载荷或流载荷的方向发生偏转时，对应的相对平衡位置也会发生偏转，但不一定朝向外载荷偏转的方向，这可能是因为外载荷矢量的偏转使风-浪-流耦合载荷的矢量方向发生了临界变化，因此其偏转方向也发生相应改变。

控制其他参数不变，风速的增大可使三浮体系统达到准静态平衡的位置变化较大，在某速度临界值，其排列方式可能发生彻底的变化，这说明风速的增大也使风-浪-流耦合载荷的矢量方向发生临界变化。较大的风速会使能够达到准静态平衡的角度区间更窄，这说明在海面上风速较大的情况下，CTV的原油转驳过程会相对困难，要想保证与常规油船之间位置的相对平衡需要DP系统更精确的调整。

通过求解带约束的单目标非线性优化问题，可得到三浮体系统保持稳态平衡时船体之间的入射角和CTV推进器需要提供的最小横荡推进力，结果表明：船首与正北向夹角φ1、φ2和φ3在该环境载荷作用下较大，而缆绳与船首和船尾的夹角α1、θ1、θ2和α3则保持相对较小的值，在这样的情况下才能保证缆绳中的张力始终保持绷紧且不产生较大艏摇；缆绳中的张力远大于CTV推进器的推力，CTV对常规油船的牵引起主要作用，而拖船提供的牵引起辅助稳定作用。