圆筒型FPSO砰击预报模型及响应特性

徐晨峰, 李 俊, 卢文月*, 李 欣, 田新亮, 毛竞航

(1. 上海交通大学 海洋工程国家重点实验室, 上海 200240;2. 上海交通大学 三亚崖州湾深海科技研究院, 海南 三亚 572000)

0 引 言

现有的石油资源难以满足人类日益增长的需求，世界各国纷纷将远洋深海石油开采作为获得稳定能源的重要方向[1]。随着水深增加，各类新型浮式平台不断涌现[2]，包括张力腿平台(Tension Leg Platform，TLP)、单立柱平台(Spar)、浮式生产储卸油装置(Floating Production Storage and Offloading，FPSO)和半潜式平台。FPSO以建造质量高、开采风险低、生产模块组合灵活及可重复使用的特点广泛应用于海上油气开采中，其中船型FPSO已成为海上油气开发的主要生产方式。但船型结构在性能上有一些不足[3]，例如单点系泊设备费用高昂、细长船体在随浪时中垂和中拱弯曲载荷很大等。由挪威Seven Marine公司设计的圆筒型FPSO在性能上有所改善[1]。但由于在深海中极端天气出现更频繁和海床沉降等[2，4-6]，平台所受到的各种极端载荷也不断频繁出现。近几十年海洋平台在运行期间遭受重大破坏的报道越来越多，其中波浪砰击载荷是海洋结构物使用期间受到的最严重载荷之一，因此对典型的圆筒型FPSO砰击响应特性进行研究，构建合适的砰击模型进行砰击载荷预报对于防范海洋平台遭受严重损伤具有十分重要的意义。

波浪砰击载荷的特点是：幅值大、持续时间短、具有高度动态特性[7]，在一个仔细控制的破波试验中发现，即使初始条件相同，在垂直面上产生砰击载荷的变化也很大[8]，这种不确定性是因为破波前部形状和裹挟空气具有固有随机性，所以应将砰击载荷本身当作一个随机过程，很难建立一个入射波对应的特征波冲击载荷。而且，波浪砰击载荷作为一种强非线性载荷，其百年一遇的载荷往往不是在百年一遇的海况下所产生的[9]，这对砰击载荷概率和载荷量级的预报有着很大的挑战。在进行海洋结构物设计时采用的砰击载荷是特定量级的返回周期载荷水平，这种方法通常先筛选返回周期的控制海况，再将载荷水平近似为控制海况的适当概率负载水平。比如对于温带恶劣环境中百年一遇的设计载荷，通常认为在5～10个百年一遇3 h海况中发生一次，在数学概率统计上即为80～90分位值[10]。采用上述方法估计特定返回周期的载荷水平很困难，这是因为载荷在分布中的分位值很高，而且这个分位值本身是未知的[11]。在分位值未知的情况下，计算具有特定返回周期概率的冲击载荷需要进行包含所有海况的长期分析，而在模型测试中进行完整的长期模拟几乎不可能。LIAN等[12]使用一些3 h海况数据集分析短期响应统计参数，这些参数在长期响应分析中有着重要作用。将参数通过轮廓线法与海况参数联系并构建联合概率密度，根据这个概率密度分布图，可进行长期模拟。魏凯等[13]基于试验数据构建跨海桥梁高桩承台波浪砰击模型，建立波浪冲击载荷时程模型，给出冲击载荷峰值和冲击上升段持续时间的边缘分布以及基于Copula的联合概率分布形式。ZHANG等[14]基于悬垂甲板的方柱试验数据，研究砰击参数对砰击压力的影响，认为方柱的倾斜在一定程度上降低砰击载荷强度。SOARES等[15]对带有外翻结构的FPSO砰击响应特性进行研究，发现海况的有义波高对砰击没有显著影响，砰击概率与波陡有高相关性，撞击位置由波峰和FPSO运动共同决定。

基于上述研究现状，本文研究对长期模拟有重要贡献的短期预报参数，采用无因次化模型探究波浪砰击与入射波波面升高之间的统计关系，构建合适的砰击载荷统计模型，旨在获得基于模型试验数据的无因次化砰击概率模型和无因次化砰击载荷分布模型，为长期模拟提供基础。

1 模型试验

试验所用的圆筒型FPSO平台由1个圆筒主体和3个垂荡板组成，如图1所示。由于模型试验的主要目的是研究圆筒型FPSO平台在恶劣海洋环境下的波浪砰击载荷参数，因此只考虑生存载况。图1中外轮廓线拐角处是圆筒的垂直外壁与倾斜外壁的交叉处，位置1～位置5从低到高分布在外翻结构上。圆筒型FPSO的技术参数和砰击测点位置如表1所示，浪高仪布置在距离圆筒中心53.928 m处，此处比圆筒型FPSO外翻结构外缘远，认为受到波浪砰击在圆筒型FPSO上的波浪反射较小。

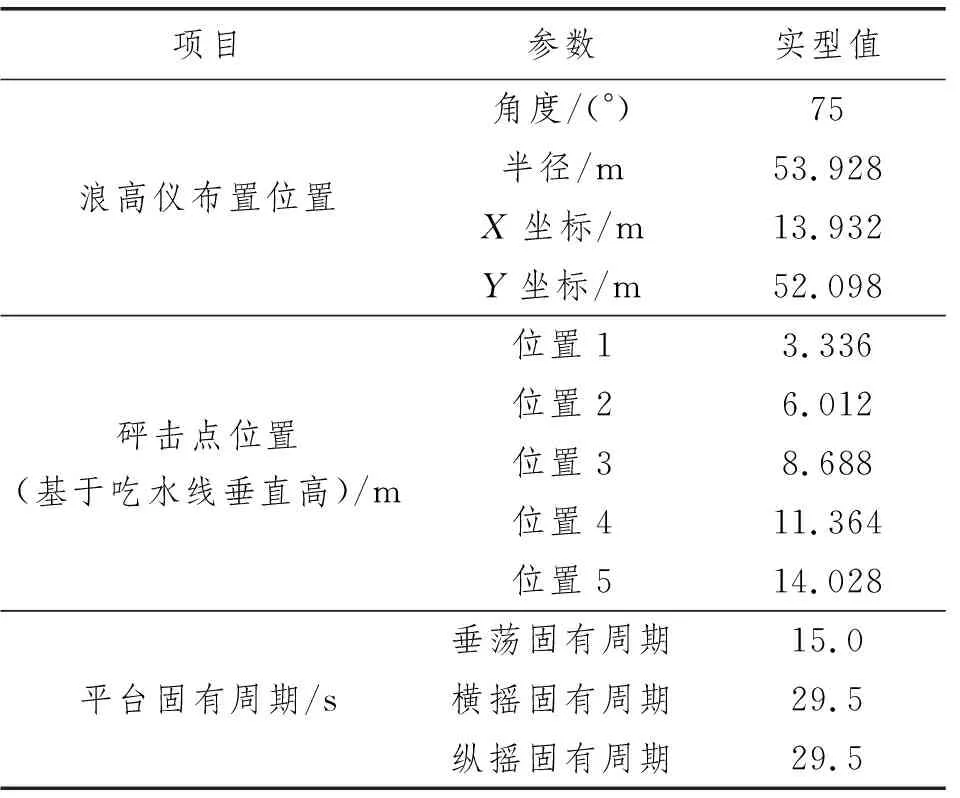
表1 FPSO平台参数和试验仪器布置位置

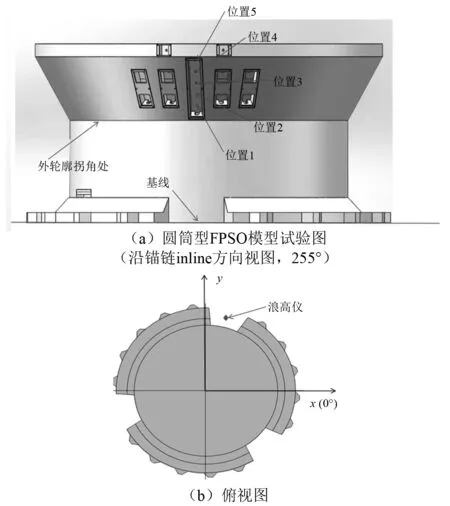
图1 圆筒型FPSO模型

基于不同波高、谱峰周期和谱峰系数的JONSWAP谱所产生的不规则波场，综合考虑在极端海况和敏感波浪周期环境下新型圆筒型FPSO的生存能力，选择百年一遇、千年一遇海况，由于砰击载荷的固有随机性，采用一海况多种子工况，环境具体参数如表2所示，其中不同种子数对应不同的波浪时历。

表2 波浪参数

由于圆筒型FPSO是浮动式平台，难以直接获得激发砰击的入射波绝对波面升高，可将迎浪面方向的浪高仪获得的相对波面升高转化为绝对波面升高。具体方法为将浪高仪测点相对于平台的位置和平台的绝对运动转化为浪高仪测点的绝对运动，浪高仪测点的绝对运动和浪高仪测得的相对波面升高之和即为入射波的绝对波面升高，隔一段距离进行相对波面升高的测量可避免波浪受到局部上升效应的影响。转化方式如图2所示。

图2 绝对波面升高、相对波面升高、平台垂向运动时历

2 结果与讨论

2.1 砰击载荷概率模型

2.1.1 圆筒型FPSO波浪砰击载荷短期概率模型

为探讨在短期预报过程中砰击载荷发生概率与平台迎浪波面的统计学关系，对百年一遇纯波浪、千年一遇纯波浪和百年一遇波流耦合海况的试验数据进行分析，采用100 kPa作为砰击载荷阈值。

分析对比百年一遇纯波浪系列海况中以100 kPa为阈值的入射波绝对波面升高cd波峰数、产生砰击载荷的波峰数和产生砰击载荷的波峰数与入射波绝对波面升高波峰数的砰击概率F，采用JOHANNESSEN等[16]研究中的式(1)模型对砰击概率进行拟合，两者共同拟合为砰击概率曲线(见图3)：

图3 百年一遇纯波浪砰击概率与绝对波面升高

(1)

式中：P为砰击载荷；P0为砰击载荷阈值，即大于阈值的砰击载荷为有效砰击；δ和θ为所需拟合的参数；k1为波数，在假定满足深水中色散关系下由平均周期T1计算得到：

(2)

式中：平均周期T1根据0阶和1阶谱矩所得

(3)

(4)

式(3)和式(4)中：m0为0阶谱矩；m1为1阶谱矩；mr为r阶谱矩；ω为频率；s(ω)为频谱。

构建相同海况下不同砰击点的概率模型拟合曲线，如图4所示。

图4 各海况不同位置砰击概率与入射波绝对波面升高的关系模型

在图4(a)中对比位置1～位置5的砰击概率拟合曲线可知：开始发生砰击时的入射波绝对波面升高为4.5～14.5 m，激发砰击的最小波面升高与砰击测量位置高度呈正相关关系；但当砰击点垂直位置较低时，开始发生砰击的入射波绝对波高高于静水时砰击点高度；当砰击点位置较高时，开始发生砰击的入射波绝对波面升高则低于静水时砰击点高度。在图4(b)中对比位置1～位置5的砰击概率拟合曲线可知：开始发生砰击时的入射波绝对波面升高为4.5～12.5 m，激发砰击的最小波面升高与砰击点高度也呈现与百年一遇纯波浪中相同的规律，说明此规律具有一定的普适性。

对比位置1～位置5，在百年一遇海况中入射波绝对波面升高开始进入砰击概率快速上升的拐点为18.5～21.5 m[见图4(a)]，在千年一遇海况中入射波绝对波面升高开始进入砰击概率快速上升的拐点为18.5～22.5 m[见图4(b)]，发现砰击概率快速上升的拐点集中在18.0～22.0 m，砰击概率开始进入快速爬升与砰击点的位置没有相关性，与海况的统计数据也没有相关性。在入射波绝对波面升高较低的情况下，发生砰击的概率随着砰击点的位置变高而减小，但进入砰击概率快速上升期后，在百年一遇纯波浪海况下，高位砰击点的概率会极速上升甚至超过低位砰击点的概率，这是由于圆筒型FPSO纵摇所造成的砰击点与波浪的相对运动比低位砰击点更快，砰击概率受自身运动显著影响。

在波流耦合工况下，在相同的入射波波面升高情况下，砰击概率随着测点位置的升高而减小[见图4(c)]，随着入射波的波面升高，其概率曲线与百年一遇纯波浪相比曲线之间的交点较少，分层性较好，说明流载荷减少了圆筒型FPSO砰击概率分布情况的突变性。

构建相同砰击位置不同海况下砰击概率模型拟合曲线，如图5所示。

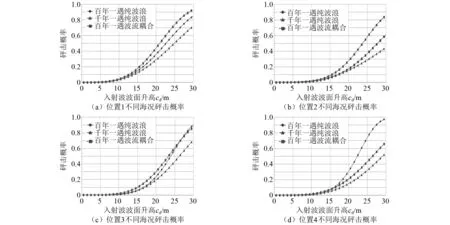
图5 各砰击位置不同海况砰击概率与入射波绝对波面升高的关系模型

对比位置1～位置3，在相同入射波绝对波高升高的条件下，百年一遇波流耦合的砰击概率在总体上比百年一遇纯波浪的砰击概率大，表明流载荷的存在增大了较低位置砰击发生的概率[见图5(a)～图5(c)]，但在较高处的位置4，流载荷减小了砰击概率[见图5(d)]。在位置1～位置4中，百年一遇纯波浪的砰击概率在总体上比千年一遇纯波浪的砰击概率更大，平台的垂荡固有周期为15 s，与百年一遇纯波浪海况谱峰周期接近，形成共振，由于圆筒型FPSO的外翻结构特点，共振使外翻结构相对波浪速度提高，从而增大砰击概率。

其中，根据式1拟合的砰击概率曲线参数δ和θ如表3所示。

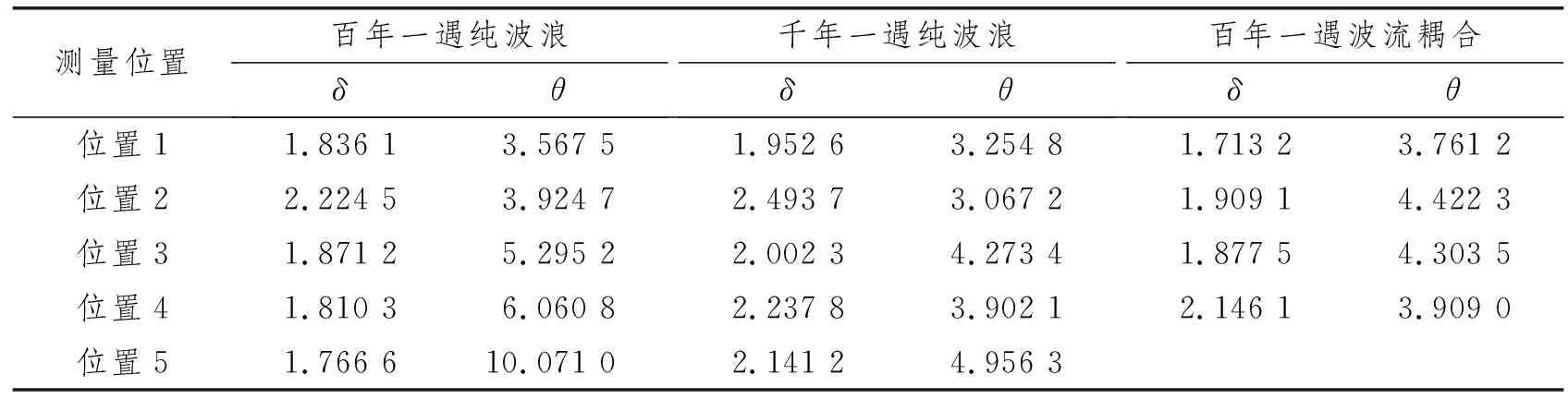
表3 各海况各砰击位置砰击载荷概率模型参数

2.1.2 无因次化阈值参数砰击概率模型

根据JOHANNESSEN等[16]，拟合参数θ对于海况统计值有很强的相关性，原因是在不同海况下砰击载荷阈值选取是一个相同的常数。使P和P0无因次化可消除θ对于海况标准差的线性关系，从而将不同海况数据拟合在一起。无因次模型拟合参数为δ′和θ′：

(5)

式中：

(6)

式中：ρ为水的密度；vc为特征水质点速度，其计算式为

(7)

式中：vc由入射波的相位速度与质子速度组合控制；标准差σdw和平均周期T1w为未受到扰动的波浪参数，此处采用校波的波浪数据；γ为控制的权重，此处简化计算，使γ=1。

图6为百年一遇纯波浪海况下不同位置砰击概率模型无因次化曲线。

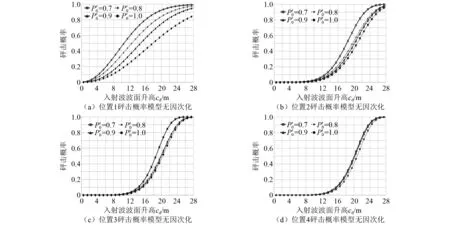
图6 百年一遇纯波浪海况下不同位置砰击概率模型无因次化

由图6可知：在砰击模型概率无因次化后，随着阈值提高，各高度砰击点的砰击概率减小，随着砰击点位置的升高，各阈值的砰击概率模型曲线变得更密集，说明随着砰击点的升高，砰击载荷的量级在总体上呈上升趋势。这是因为，随着阈值的提升，各无因次阈值的概率曲线越集中，则说明砰击载荷量级的总体越高。

构建包含多海况的无因次砰击概率模型，将各海况中相同阈值的无因次参数拟合在同一砰击概率曲线中，如图7所示。

图7 不同位置砰击概率模型无因次化

由图7可知：当砰击点较低且靠近平台外轮廓拐角时，无因次砰击概率曲线随阈值的提升产生强烈的变化[见图7(a)]，当远离外轮廓拐角时，无因次砰击概率曲线会更密集[见图7(b)～图7(d)]，说明由于在水线位处并且在圆筒型结构外轮廓拐角处的砰击载荷随机性显著提升，平台结构外形对砰击概率有巨大影响。

所拟合参数θ′和δ′如表4所示。由表4可知：参数θ′随着砰击点高度提升而增大；参数δ′在位置1的砰击点随着阈值P′0的增大而增大，但在砰击点2～砰击点4中没有太大改变。

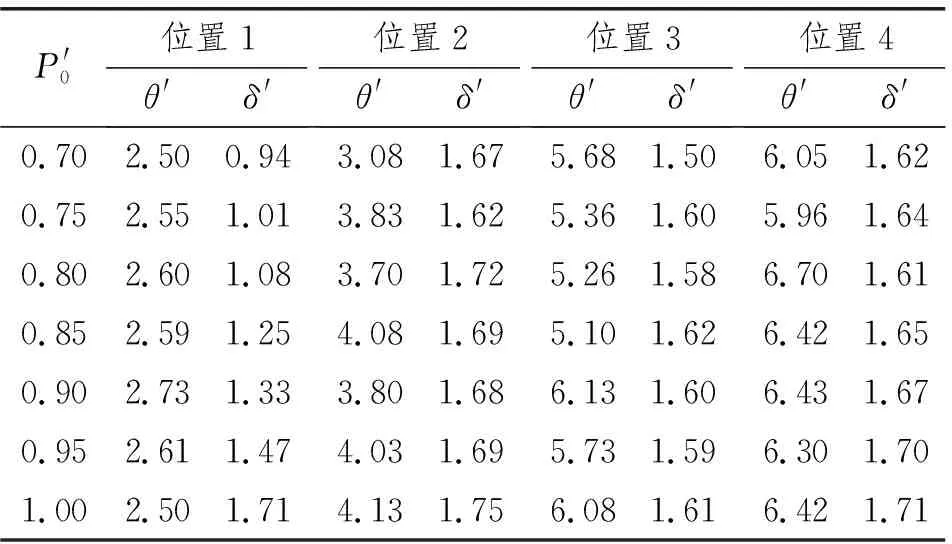
表4 各砰击位置砰击载荷概率无因次化模型参数θ′和δ′

2.2 波浪砰击载荷分布模型

在已产生的砰击中，采用砰击数据探究波浪砰击载荷分布。砰击载荷的分布满足威布尔分布：

(8)

式中：g为重力加速度；α和Cs为参数。根据JOHANNESSEN等[16]，参数α和Cs对于海况没有明显的依赖性，可将各海况数据集中拟合。各砰击点的载荷分布如图8所示，其中C为式(8)中的0.5ρgcd。模型参数α和Cs如表5所示。

表5 各砰击位置砰击载荷分布无因次化模型参数α和Cs

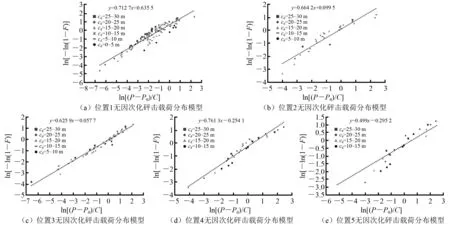
图8 无因次砰击载荷分布模型

由图8可知，在各入射波分段中所激发的砰击载荷在横坐标上分布比较广泛。这说明由于波浪破碎的存在，浪头裹挟空气的固有随机性造成砰击载荷的随机性非常强，对于破波载荷与非破波载荷鉴别方法有进一步研究的必要。随着位置的提升，激发砰击的最小入射波波面升高也在提高。在位置1～位置4中，激发砰击的主要波浪高度为15.0～20.0 m，可认为入射波波高为15.0～20.0 m的波形容易造成砰击载荷。

由表5可知：参数α与砰击点的高度无明显关系；参数Cs与砰击点的高度有正相关性。

2.3 波浪砰击载荷空间分布

由于测得的砰击载荷数据来自固定于圆筒型FPSO上的各测点所测得数据，探究波浪冲击载荷的垂直空间分布，则有：

(7)

式中：c′为砰击点的垂直高度与相对波面升高crel之差由入射波绝对波面升高归一化；Zc为静水线(SWL)上方砰击点的垂直位置。探究相对波面升高与砰击点的垂直高度差对砰击载荷分布的影响。

根据c′绘制的所有砰击点和所有海况下的波浪砰击事件如图9所示。

图9 波浪砰击载荷空间分布

所观察到每个砰击点所受到的最大载荷发生在相对波面升高略低于面板的高度。位置1处于外翻结构较低位置处，在图9中表现为横坐标分布广泛，在横坐标大于零的范围内存在许多，说明在外翻结构的外轮廓拐角处，当入射波相对波面升高小于位置1的垂直高度时，也能激发许多砰击，外翻结构拐角处的局部上升效应十分强烈。由位置2～位置5可知，随着位置的升高，横坐标越来越集中，说明在远离外翻结构的拐角处，激发砰击的入射波波面升高越来越集中在特定范围内。

3 结 论

针对圆筒型FPSO的砰击载荷响应，采用砰击概率模型、无因次化砰击概率模型和无因次化砰击载荷分布模型探究入射波波面升高与砰击概率、砰击载荷量级的关系。对比砰击载荷空间分布、不同海况的概率模型，得到结论如下：

(1)针对不同海况下的砰击载荷研究，圆筒型FPSO激发砰击的最小波面升高与砰击点的高度呈正相关性，但砰击发生概率在快速爬升阶段与砰击点的位置没有关系，与海况的统计数据也没有关系。随着砰击点位置的提高，圆筒型FPSO砰击载荷在总体上呈上升趋势。

(2)平台砰击概率受自身运动影响显著，对于运动幅度较大的浮动式平台，在构建砰击概率模型时，需要考虑平台运动参数。砰击概率受平台垂荡运动固有周期影响显著。

(3)随着位置的提高，激发砰击的入射波波面升高越来越集中在特定范围内，在本模型中为15.0～20.0 m。

(4)对于所构建的无因次砰击概率模型，在拐角处的模型参数δ′会随着阈值的提高而变大，在远离拐角处的δ′较为固定，θ′会随砰击位置的提高而增大。无因次砰击分布模型参数α与砰击点高度无明显关系，Cs与砰击点高度有正相关性。

本文借鉴JOHANNESSEN的方法，采用基于入射波波面升高无因次化砰击模型，探究砰击概率分布、砰击载荷分布和砰击空间分布。与前人对于TLP平台的研究不同，由于圆筒型FPSO有更明显的垂荡运动和独特的外翻结构，探究其方式的使用和砰击载荷特性，在之后的研究中可考虑增加运动的变量和更多的模型试验以研究模型的置信度。对于砰击载荷分布，可考虑运用大量的模型试验，划分合适的破波和非破波砰击分类方式，分别构建模型。