海洋工程平台齿轮箱齿轮本体温度场仿真

陈 峰, 吴平平, 吴 韩, 徐天殷

(1. 佛山市南海区知识产权协会, 广东 佛山 528000;2. 广东精铟海洋工程股份有限公司, 广东 佛山 528000)

0 引 言

海洋工程升降平台齿轮箱单元传动效率高，在整个海洋工程平台升降系统中起着重要的作用。海洋工程升降平台齿轮箱运行时会产生大量的热量，由此导致轮齿齿面产生局部高温，会增加齿轮啮合的齿面产生热粘连、造成齿面材料剥落的热胶合风险，进而导致齿轮啮合齿面产热量增大的恶性循环，导致海洋工程平台齿轮箱传动噪声大等不利的影响，使传动性能降低。分析齿轮啮合产生及传热的机理对于提高海洋工程升降平台齿轮箱的传动性能具有重要意义。

王春华等[1]采用控制变量法分析高速齿轮各相关因素对其本体温度场的影响，并在此基础上计算修形斜齿轮本体温度场。李子繁等[2]利用基于LS-DYNA软件的热-固耦合方法，研究齿轮啮合摩擦发热的原理，结果表明，齿轮啮合的热生成率是沿着齿宽方向变化的，热生产率在齿宽中线处最高，温度梯度从中间向两边降低。但李子繁等只研究一组齿轮的齿轮啮合摩擦生热机理。谭富星等[3]以某新型高速动车组齿轮箱的不同齿轮为研究对象，分析齿轮箱中不同齿轮的温度分布情况，并通过台架试验验证仿真结果的正确性。王伟等[4]基于ANSYS对弧齿锥齿轮温度场不同模数和齿宽的齿轮本体温度场进行分析，有限元结论表明，当齿宽增加时本体温度升高，但本体温度分布情况未发生变化。汝学斌等[5]依据赫兹接触理论和摩擦学原理，分析齿轮副本体温度场的分布，得出在热弹耦合接触分析齿廓修形对齿面温度场的影响中，在主动轮和从动轮总变形中周向变形占主要部分，变形主要分布在齿面接触位置，径向和轴向变形分布趋势与热变形趋势相似。张宝利等[6]基于热学理论详细计算斜齿圆柱齿轮端面和齿面的对流换热系数，采用Ansys和Solid Edge软件分析斜齿圆柱齿轮本体温度场的分布情况，对优化重载齿轮设计有一定的指导意义。王振等[7]将赫兹接触理论与有限元接触理论相结合，系统分析高分子齿轮齿面接触压力，研究齿轮啮合过程中轮齿的齿面摩擦因数和摩擦热流密度的计算方法，其分析直观地了解0.1 s时刻内温度随时间的变化。蔡瑜瑜[8]将传热学与摩擦学基本原理相结合，对弧齿锥齿轮啮合摩擦的非稳态本体温度场进行分析，试验表明：齿轮润滑系统的失效会导致齿轮啮合发热量增加，温度升高，直至齿轮发生热胶合而失效。任敏强等[9]以某重载机车驱动系统圆柱直齿轮为研究对象，以齿轮啮合的转速为设计变量，研究齿轮啮合在不同转速下的齿轮本体稳态温度场，为提高齿轮强度和轮齿修形及优化设计提供理论支持。樊智敏等[10]将摩擦学、传热学与齿轮啮合原理相结合，提出以轮齿摩擦接触所释放的能量为热源，计算摩擦接触的热通量和对流系数，以变位系数为设计变量，分析得出切线变位系数增大会使得齿面最大温度有所下降，但切向变位系数过大也会导致温度升高。李想[11]给出弧齿锥齿轮稳态本体场分布的影响因素。弧齿锥齿轮啮合具备连续性，摩擦热流密度随着传动着力点的移动而变化，李想等将所计算的摩擦热流密度作为加载条件加载至单齿弧形本体温度场上，得到较好的弧形锥齿轮本体温度场的变化图。该方法适用于研究海洋工程装备齿轮箱直齿轮啮合本体温度场。李磊[12]将渐开线圆柱塑料斜齿轮替代普通蜗轮蜗杆传动中的蜗轮，发现随着负载的增加，接触区域将由一个点扩展成一个椭圆形的区域。在不同材料下，齿轮摩擦发热情况及传热系数是不同的，李磊的研究表明：随着载荷和转速的增加，齿面温度也升高，由齿面温度升高导致的最大变形量增加显著。

综上所述，将摩擦学、传热学相结合的齿轮啮合轮齿本体稳态温度场分析可为海洋工程齿轮箱齿轮啮合稳态温度场分析提供参考。本文结合齿轮本体稳态温度场相关理论，以不同转速和不同扭矩的海洋工程齿轮箱的工况为研究对象，通过理论计算出齿轮发热量和热对流系数，结合有限元软件，使用Solid 186单元对齿轮啮合的稳态温度场进行分析。

1 齿轮本体温度场分析理论

海洋工程齿轮箱经过跑合阶段后，齿轮传动产生的大部分摩擦能量转化为热能，经过齿轮本体和润滑油的热传导及热对流作用，以齿轮箱冷却水等方式散热后，齿轮啮合的产热量与热传导及热对流的散热量相等，达到齿轮箱正常转动的热平衡。此时海洋工程齿轮箱的温度场即视为稳态温度场。

当齿轮啮合时，由齿面啮合产生的瞬时高温的影响范围小，远小于接触区的宽度，且作用时间极短，可忽略不计。齿轮啮合在不同扭矩和转速下，齿轮本体产生的热量不一样，齿面产生的变形不一样，造成齿面接触面积会产生变化，但由于齿轮啮合发热是单位时间内随着转速的升高造成齿轮啮合次数的增多，在微观上齿面来不及散热，因此可看成一个连续发热的热源。轮齿齿面可看作以点或椭圆区域接触区发热的高频发热热源。排除制造误差、材料缺陷等因素的影响，齿轮上的每个轮齿发热情况相同。高频点或椭圆区域发热热源在每个轮齿齿面的温度分布情况相同。在正常工作状态下，排除外部冲击的影响，齿轮轮齿受到的转速和扭矩维持不变，即齿轮啮合高频发热热源在每次齿轮啮合时发热量是稳定的。在分析时，只需要分析单个齿的温度场即可。

根据Block理论，由李子繁[12]的齿轮摩擦产热瞬态仿真温度云图可知，在不考虑热传导时，齿轮啮合产生的热量主要集中在齿根和齿顶，齿轮啮合区域的温度明显大于非啮合区域的温度。齿轮啮合产热区集中于齿面之间的摩擦区域及齿轮本体传力区域。传力区域的材料发生应变后，有一部分结构的弹性势能转化为热能。因此，齿轮啮合产生的热量集中于齿面上，在齿根圆以下2.5倍模数区域后，基本不传力，其发热情况可忽略不计。

选取轮齿部分及齿根圆以下2.5倍模数区域进行计算。图1所示为单个齿轮的计算区域。

图1 单个齿轮的计算区域

对于海洋工程齿轮箱齿轮啮合的齿轮本体，其无内部热源，其属于稳态温度场，导热的偏微分方程为

(1)

式中：T为齿轮本体温度，℃；x、y、z为坐标，m。

稳态温度场的产热量与散热量相等，其温度分布只与稳态时的边界条件有关，温度场问题是边值问题。只需要按照稳态温度场的特点给出边界条件，即可计算稳态温度场温度分布。传动齿轮的稳态本体温度须符合下列边界条件：

在齿轮啮合工作齿面上，当齿轮啮合时，因齿面摩擦生热，会有热量q的输入，同时齿轮会与空气发生接触，存在齿轮与空气的热传导效应，其边界条件为

(2)

式中：λ0为齿轮材料的导热系数，W/(m·K)；n为热交换面的外法线方向；a为齿面的换热系数，W/(m2·K)；T0为环境温度，℃；q为沿齿轮的啮合工作面输入的摩擦热流量，W/m2。

在齿轮端面上，主要是端面与空气之间的换热，而没有摩擦热量q的输入，因此其边界条件为

(3)

式中：as为齿轮端面的换热系数，W/(m2·K)。

在其他面如齿顶、齿根及非齿轮啮合工作齿面上，由于齿轮啮合使齿轮齿体的温度升高，从而使该区域与空气产生热传导，其边界条件为

(4)

式中：at为齿根、齿顶及非齿轮啮合工作齿面的换热系数，W/(m2·K)。

在齿轮底部界面上，由于底面距齿轮啮合面较远，越靠近轴心，温度梯度越小，热量的传导率低，可忽略不计，其相当于绝热表面的边界，即

(5)

分齿截面虽存在着热量的传导，但单个齿研究的温度场可作为齿轮内部问题处理，并且齿与齿之间的分齿截面表面上传导的热量的数值相等，其边界条件为

(6)

2 热边界条件计算

在计算海洋工程齿轮箱齿轮稳态温度场温度分布时，需要确定啮合面热对流系数、端面的对流换热系数及摩擦产热机理下的热流密度与热量分配系数。

2.1 深水飞线安装分类

直齿轮啮合面与润滑油的对流换热因数h为

(7)

式中：λ1为润滑油的导热因数；Re为润滑油的雷诺数；Pr为润滑油的普朗特数；d为齿轮的节圆直径，mm。

2.2 端面对流换热系数分析

将齿轮端面等效为圆盘模型，根据雷诺数Re的不同，润滑油沿圆盘的流动的对流换热系数计算公式也不相同。

层流(Re<2×105)时，端面的对流换热因数为

(8)

式中：k为润滑油的热传导率，W/(m·K)；m为指数常数；ω为齿轮旋转加速度，rad/s；υ0为润滑油的运动黏度，m2/s。

过渡层流(2×105≤Re≤2.5×105)时，端面对流换热因数为

(9)

式中：rc为齿轮端面上的任意半径，mm。

紊流(Re≥2.5×105)时，端面对流换热因数为

(10)

2.3 摩擦热流密度分析

齿轮齿面之间的摩擦机理较为复杂，主要分为滑动摩擦、滚动摩擦和金属弹塑性变形的内摩擦。滚动摩擦相当于在齿面形成微观的楔形油膜，因此其发热量较少，可忽略不计。在材料比例屈服阶段，金属弹塑性变形的弹性应变能较非弹性应变能小，金属弹塑性变形后，接触面积增大，接触应力减小，因此内摩擦产生的热量很少，可忽略不计。由滑动摩擦产生的平均摩擦热流密度q为

q=f0Fav|v1-v2|

(11)

式中：f0为滑动摩擦因数；v1和v2为2个齿轮啮合时啮合点上的切向速度，mm/s；Fav为齿轮啮合点接触区平均压应力，N/m2，其计算式为

(12)

齿轮啮合点接触区最大接触压应力FHz的计算式为

(13)

式中：E′为综合弹性模量，Pa；Pca为沿齿面接触线上单位长度上的计算载荷，N；R为齿轮啮合点综合曲率半径，m。

综合弹性模量E′计算式为

(14)

式中：E1和E2为齿轮啮合齿轮的两种材料的弹性模量；N/m2。

齿轮沿齿面接触线单位长度上的计算载荷Pca计算式为

(15)

式中：K为齿轮传动时的载荷因数；Fn为作用于齿面接触线上的法向载荷，N；L为沿齿面接触线总长，m；B为齿轮宽度，m；εα为齿轮传动的重合度；α为齿轮的压力角。

齿轮端面分度圆上的圆周力Ft为

(16)

式中：Ft为圆周力，N；T1为齿轮的转矩，N/m；d1为分度圆直径，mm。

齿轮传动的重合度εα计算公式为

(17)

式中：Z1和Z2分别为主从动齿轮齿数；αα1、αα2分别为小、大齿轮的齿顶圆压力角。

齿轮传动的载荷因数的计算式为

K=KAKvKβKα

(18)

式中：KA为使用因数，又称工作情况因数；Kv为载荷因数；Kβ为载荷分布不均因数；Kα为齿轮啮合齿间载荷分配因数。

高速转动的啮合齿轮比润滑油流动的速度快，齿面上由润滑油带走的热量很少，且金属的传热效率远大于润滑油的传热效率，由齿轮齿面经过润滑油传导散热的热量可忽略不计。可假设由齿轮摩擦及齿轮本体变形产生的热量全部经过齿轮的端面大面积与润滑油接触散热。可将齿轮齿面摩擦热q分作两部分q1和q2，分别流入2个传动齿轮。

齿轮啮合的主动轮与从动轮一般采用不同的材料，其导热系数存在差异。且齿轮啮合时，主、从动齿轮的啮合变形也存在差异，导致由摩擦及齿轮材料变形的产热量传导至主、从动齿轮上不相等。一般引入热分配因数β。2个齿轮各自输入的热量为

(19)

热分配因数β为

(20)

式中：λ1和λ2为2个齿轮的导热系数，W/(m·K)；ρ1和ρ2为2个齿轮材料的密度，kg/m3；c1和c2为2个齿轮材料的比热容，J·kg-1·K-1。

传动啮合的一对齿轮传动时产生的热流可选取平稳旋转状态下的平均值作为主、从齿轮的平均热流输入，分别为q1、q2：

(21)

(22)

式中：b为齿轮啮合点处接触半宽，m。

3 海洋工程平台齿轮箱齿轮稳态温度场有限元分析

以某海洋工程平台齿轮升降系统齿轮箱单元模型为仿真对象，采用有限元软件Ansys Workbench对该平行齿轮箱单元中的高速传动轴直齿圆柱齿轮副进行稳态温度场仿真分析，得到该齿轮箱高速传动轴齿轮副主动轮和从动轮的稳态温度场分布情况，并对所得到的有限元温度场结果进行分析。

3.1 三维模型建立

在对海洋工程平台的电机齿轮升降系统齿轮箱齿轮啮合的本体温度场进行分析时，选取平稳状态下一周的平均热流分别输入主、从轮上，只需要对单个齿进行分析即可。选择在SolidWorks中建立各级齿轴齿轮的单齿模型。图2和图3为主动轮和从动轮的单齿模型。

图2 主动轮单齿模型

图3 从动轮单齿模型

3.2 材料定义及划分网格

在该齿轮箱单元中，高速传动轴主动轮所用的材料为38CrMoAl，从动轮所用的材料为42CrMo。其相关参数如表1所示。

表1 齿轮材料参数

在Engineering Data模块中建立表1所述的材料及相关系数，并将材料属性赋予模型，完成材料定义。

齿轮轮齿发热集中在轮齿齿面，从齿根至齿顶不同位置的发热量具有差异，选择Solid 186单元网格如图4所示，齿面网格密集，非齿面网格可相对稀疏，Solid 186是一个高阶三维20节点固体结构单元，具有二次位移模式，可更好地模拟不规则的网，更贴近分析模型。

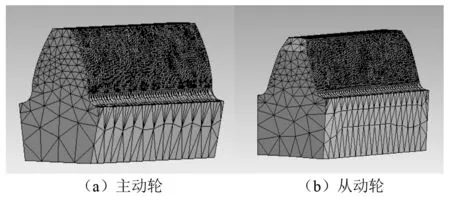
图4 齿轮热分析网格划分

3.3 热边界条件设置

在齿轮齿轴生热量及对流换热系数研究的基础上，计算正常工况下(主动轮转速为15 118.6 r/min，扭矩为115.8 N·m)的主、从动轮的摩擦热流密度和不同面的对流换热系数，其数值如表2所示。

表2 主、从动轮热流密度与对流换热系数

3.4 齿轮稳态温度场仿真

运用Ansys Workbench中的稳态热分析模块对齿轮单齿本体温度场进行仿真分析。先将由理论计算得到的平均热流密度分别加载至主、从动轮的啮合面上，然后在主、从动轮的啮合面、端面等面上分别加载相应的对流换热系数，再在Steady-State Thermal模块中进行稳态温度场分析，得到齿轮的稳态温度场分布情况如图5和图6所示。

图5 主动轮单齿稳态温度场

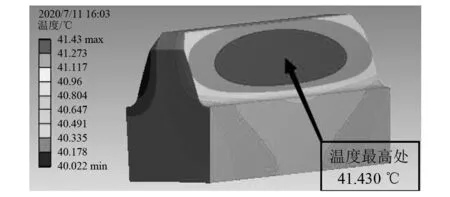
图6 从动轮单齿稳态温度场

由图5和图6可知：高温区域主要分布在啮合齿面的中间部分，啮合齿面温度整体分布从中间至周边依次降低；主、从动轮的温度分布趋势一致，但主动轮的最高温度(49.881 ℃)高于从动轮的最高温度(41.43 ℃)。产生这一现象的原因可能是主动轮单齿在啮合一圈时产生的热流密度大于从动轮，从而导致主动轮的温度偏高。

3.5 不同工况下齿轮单齿有限元分析

当转速和扭矩的不同时，齿轮啮合的摩擦热流密度也有差异，由此导致的齿轮本体的温度场也会存在差异。对不同转速(转速为500、750、1 000、1 250、1 500、1 750、2 000 r/min)和不同扭矩(扭矩为50、70、100、125、150、175、200 N/m)工况下的齿轮本体温度场进行仿真，研究齿轮箱单元高速传动齿轮副在正常工况附近的转速和扭矩对其本体温度场大小及分布的影响。

3.5.1 不同转速对齿轮本体温度场的影响

图7～图10所示为不同转速下的齿轮本体温度场温度分布图，可知随着主动轮转速的逐渐升高，其齿轮最高本体温度也逐渐升高，从动轮的本体温度也随之升高，但主动轮的温度始终高于从动轮，且主动轮的本体温度增幅也大于从动轮。

图7 主、从动轮不同转速的最高温度

由图8～图10可知：随着主动轮转速由500～2 000 r/min逐渐增大，主动轮最高本体温度分别为41 ℃、47 ℃、51 ℃，且对应的最低温度也平稳增加，没有中间存在温度突然升高等情况，但齿轮啮合齿面的整体温度分布趋势不随齿轮转速的增加而发生改变。

图8 主、从动轮单齿温度场(n=500)

图9 主、从动轮单齿温度场(n=1 250)

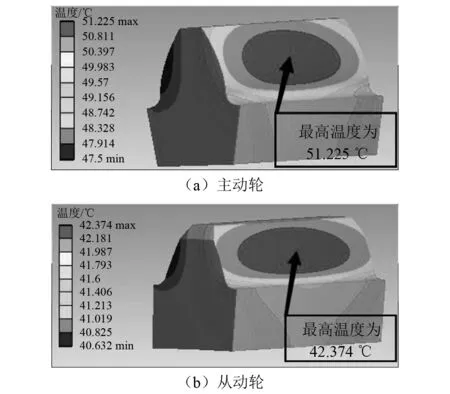
图10 主、从动轮单齿温度场(n=2 000)

3.5.2 不同扭矩对齿轮本体温度场的影响

图11～图14为不同扭矩下的齿轮本体温度场温度分布图。由图11可知，随着主动轮扭矩的逐渐增大，其齿轮本体最高温度也逐渐升高，从动轮的本体温度也随之升高，但主动轮的温度始终高于从动轮，且主动轮的本体温度增幅也大于从动轮。由图12～图14可知：随着主动轮扭矩由50～200 N/m逐渐增大，主动轮最高本体温度为33 ℃、51 ℃、68 ℃，其对应的最低温度也随之升高，但齿轮啮合面的整体温度分布趋势不随齿轮扭矩的增加而发生改变。

图11 主、从动轮不同扭矩的最高温度

图12 主、从动轮单齿温度场(T=50)

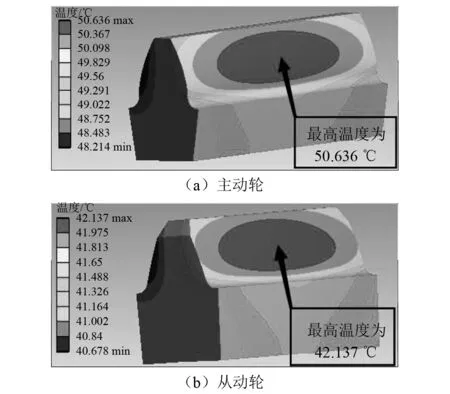
图13 主、从动轮单齿温度场(T=125)

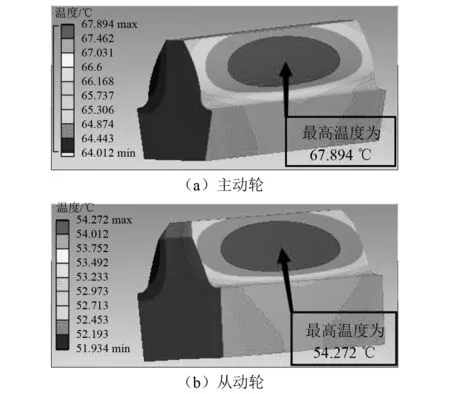
图14 主、从动轮单齿温度场(T=200)

4 结 论

采用Ansys Workbench对某海洋工程平台齿轮箱齿轮稳态温度场进行仿真分析，得出以下结论：

(1)在正常工况下，主动轮与从动轮的稳态温度场分布情况相似，最高温度分布在齿轮啮合面中间区域，往周围温度逐渐降低。但主动轮的最高温度高于从动轮。

(2)主动轮和从动轮的最高温度随着转速或扭矩的逐渐增大而升高，且对应的最低温度也升高；但主动轮和从动轮单齿本体温度场分布趋势不会随着齿轮转速或者扭矩的改变而改变。

(3)从温度变化来看，在不同的扭矩和转速下，齿面温度变化的斜率均较为平稳，没有出现突变情况，温度集中于齿面，并且向齿轮轴心扩散，但在距离齿根圆2.5倍模数的区域，齿轮温度梯度变化的影响较小。