系泊缆初始配重参数优化方法

刘东旭, 冯士伦, 毛建斌

(1. 天津大学 建筑工程学院, 天津 300350;2. 海洋石油工程股份有限公司, 天津 300350)

0 引 言

当前深水系泊缆的成分已从纯钢制锚链逐步过渡到钢缆-锚链等形式的组合缆，组合缆造价低、维修便捷，但其整体重量减小，对半潜式平台运动的约束能力变差，从而增加平台受到的二阶波浪力，导致系泊缆的系泊张力增大。因此，在保证经济性的条件下，需要尽可能地降低系泊张力。

在通常情况下，减小系泊力的优化方案包括2种，一种是改变系泊缆与平台之间的距离以控制有效长度，另一种是在组合缆的钢缆上增加配重块。张会良等[1]通过改变系泊缆的初始长度与缆索张角，将某深水圆筒型钻井平台的最大受力减小约14.8%。王庆丰等[2]改变系泊点的位置将各根系泊缆的系泊张力平均化，保证任意一根系泊缆的安全。陈映宇等[3]将浮式风机的悬链线式系泊改为绷紧式系泊，并改变系泊点的水平跨距，减小浮式风机的水平运动。冯波[4]对某大型船坞的系泊缆布置和配重块同时进行优化分配，增加配重块重量可有效降低系泊力。亓俊良等[5]采用配重链代替部分遗失的配重块，在保证系泊惯性矩不变的同时有效减小浮式生产储油船的运动冲击载荷，保证系泊系统的稳定。王领等[6]将某大型浮台的部分水下锚链替换成带配重块的钢缆，提高系泊系统的整体恢复力。徐旭等[7]对比圆筒型浮式平台带有配重块和未悬挂配重块的系泊缆张力，计算得到配重块可将系泊缆分成3段，这样的折线型系泊系统弹性提高，系泊系统张力显著减小。陈宇[8]比较浮式生产储油船系泊系统中不同配重物的重量对平台运动响应和系泊张力的影响，结果表明配重物重量过大会使系泊张力增大。肖元等[9]使用尼龙缆代替钢制锚链作为浮式风机的系泊缆，在尼龙缆上悬挂配重锚链来减小系泊力。李达等[10]综合优化系泊缆布置和配重块重量，有效减小海洋石油118系泊系统张力。

综上所述，在系泊缆上设置配重块可有效减小系泊缆张力，配重块的最佳位置和重量的设置通常根据实际情况利用经验公式得到，如果需要提高经验公式的准确性，则需要进行大量的有限元计算分析，所需时间较长。为节省计算时间，可以借助神经网络模型的泛化能力来减少非必要的有限元计算。

本文建立粒子群优化反向传播(Particle Swarm Optimization-Back Propagation，PSO-BP)模型，通过MATLAB遗传算法工具箱对半潜式平台系泊系统配重块的位置和重量进行优化计算，得到相对较优的配重位置和重量，以此为根据进行系泊系统的初步设计。人工神经网络计算较快，且具有一定的精度，满足工程需要，该方法缩短了设计时间，利用有限数据即可得到可靠的配重块设计方案。

1 概 述

1.1 平台信息

NH8平台是1艘作业于南海区域的双船体型半潜式钻井平台，共有6根稳性立柱，立柱之间有纵向和横向桁架，其主尺度参数如表1所示。

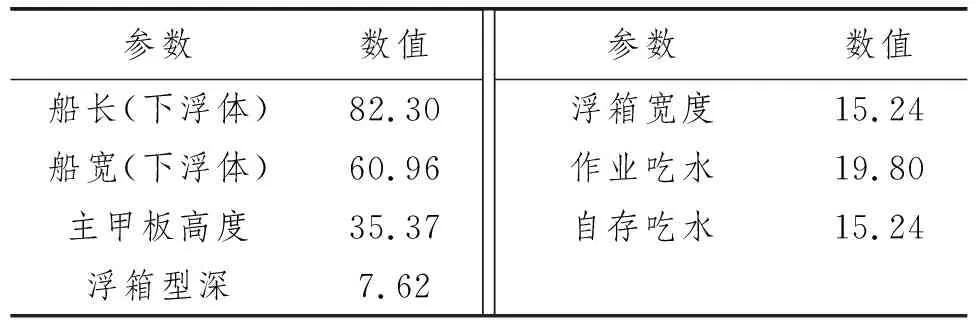
表1 NH8平台主尺度参数 m

平台的系泊系统由8根系泊缆组成，各根系泊缆材质相同，均由钢制锚链与钢缆组成，每根系泊缆由R4锚链+R5锚链+IWRC钢缆组成，具体成分与特性如表2所示，8根系泊缆沿平台长度方向对称布置，平台上设置8个导缆孔，导缆孔的坐标如表3所示。

表2 系泊缆特性

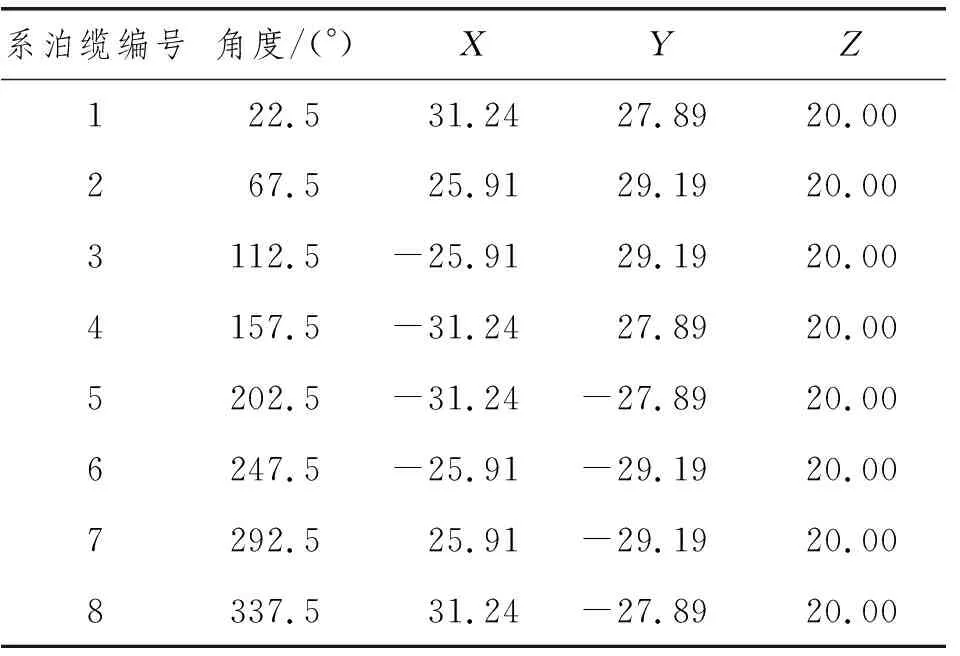
表3 导缆孔坐标

采用有限元软件MOSES对该平台进行数字建模，平台模型如图1所示。

图1 有限元模型

1.2 环境载荷

通常需要计算平台在完整作业工况和破损自存工况下的系泊力，受篇幅所限，以完整自存工况为例，取五年一遇的环境设计条件，其中，波浪载荷通过JONSWAP谱计算，风载荷通过NPD风谱计算，具体数据如表4所示。

表4 五年一遇环境条件

2 配重块优化计算

2.1 PSO-BP神经网络

PSO-BP神经网络以BP神经网络为基础，以神经网络预测输出与实际输出的均方差为适应度函数，通过PSO算法对BP神经网络的初始权值和阈值进行优化，得到较优的BP神经网络。

先确定样本数据包括输入层、隐含层、输出层节点个数以及各个节点之间的连接权值和阈值，信号通过正向传播，得到隐含层输出H。

再经过输出层计算得到预测输出O：

(1)

(2)

式(1)和式(2)中：H为隐含层输出；O为输出层输出；f为输入层与隐含层之间的映射关系；i、j、k分别为输入层、隐含层、输出层节点编号；n、l、m分别为输入层、隐含层、输出层节点个数；ωij、ωjk分别为i、j节点和j、k节点之间的连接权值；xi为输入样本；hj为第j层隐含层输出；aj、bk为第j、k节点上的阈值。

然后将神经网络的预测值与样本中的真实值的误差进行反向传播，调整对应的权值和阈值，但初始权值和阈值设置失当容易引起局部最小值问题，降低BP神经网络的预测精度，因此引入PSO算法对初始权值和阈值进行进一步优化。将BP神经网络的初始权值和阈值向量看作粒子，构建初始粒子群X，以BP神经网络预测与实际样本之间的均方差作为PSO算法的适应度函数，每个粒子X(i)都有其位置和速度，位置对应适应度，速度对应演化方向，寻优过程为

pi(t+1)=pi(t)+vi(t+1)

(3)

vi(t+1)=C1vi(t)+C2r1(t)[Pib(t)-Pi(t)]+
C3r2(t)[Pgb(t)-Pi(t)]

(4)

式中：pi(t)为粒子群中第i个粒子所在位置，其中t为寻优代数；vi(t)为第i个粒子速度；C1、C2、C3为学习系数；r1、r2为惯性系数；Pib为此粒子经过的最优位置；Pgb为种群中所有粒子经过的最优位置。通过不断更新最优位置，最终得到的Pgb就是优化后BP神经网络的初始权值和阈值。

2.2 正交试验设计

正交试验设计法以数理统计理论为基础，是一种对含有多个因素的试验进行设计优化的方法。对系泊缆上配重块位置和重量进行优化，为减少计算量、节省计算时间，且由于在工程中配重块通常处于同一水平位置，而8根系泊缆属于对称布置，因此将沿平台型长方向对称的配重块设置成同样重量。变量为配重块重量和配重块位置，将1号系泊缆和5号系泊缆的配重块重量定义为因子1，2号系泊缆和6号系泊缆的配重块重量定义为因子2，3号系泊缆和7号系泊缆的配重块重量定义为因子3，4号系泊缆和8号系泊缆的配重块重量定义为因子4，配重块与导缆孔的距离定义为因子5。经过初步计算，将配重位置设置在距离导缆孔800～1 300 m某处，重量设置为0～30 t。选用1因素6水平4因素3水平的L18正交试验表，经过拟水平化后如表5所示。

表5 正交试验设计表

以环境入射角为0°和90°为例，分别计算这18组数据，用得到的结果作为样本，在MATLAB中搭建PSO-BP神经网络。随机取另外18组配重设计的结果搭建对照组的PSO-BP神经网络，在给定范围内随机取10组试验数据，通过有限元计算得到真实响应。再分别计算2种神经网络下系泊缆张力的预测值与真实值的误差平均值，如图2所示。

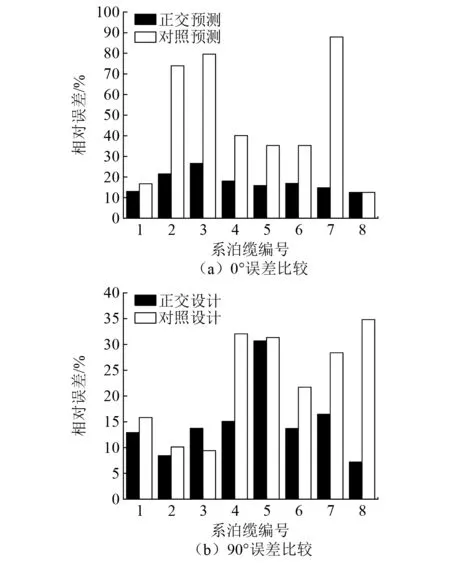
图2 2种神经网络预测结果对比

由图2(a)可知：在0°环境入射角的情况下，以正交试验数据作为样本数据的神经网络各根系泊缆的系泊张力预测输出均贴近真实数据输出，相对误差在30%以内，满足工程实际需要，除1号和8号系泊缆的系泊力输出接近之外，以正交设计数据为样本的神经网络预测其他系泊缆的结果明显优于对照组数据。由图2(b)可知：在90°环境入射角的情况下，除3号系泊缆外，以正交试验数据作为样本数据的神经网络的预测误差均小于对照组预测误差，在该环境条件下的3号系泊缆张力预测误差大于对照组，但真实系泊力为204.35 t，二者之差仅29.03 t，相对误差在15%以内，因此在可以接受的范围之内。综上所述，在相同数量的数据输入情况下，以正交试验设计法得到的样本为基础的PSO-BP神经网络优于随机选取的样本，具有一定的预测精度，满足工程实际需要。

2.3 遗传算法优化

遗传算法以达尔文进化论学说为基础，种群经过一代又一代的繁衍，在繁衍过程中不断交叉、变异，得出更加优秀的子代，对应在数学问题中即为寻找最优解的过程。对于配重块设置来说，如果计算全部配重位置和配重重量的组合的真实输出是十分不现实的，因此可以使用遗传算法对计算过程进行优化。

以0°环境入射角为例，先利用MATLAB语言编程，以正交试验设计法所得数据作为样本数据，搭建PSO-BP神经网络，再使用MATLAB中的遗传算法工具箱，以全部系泊缆的系泊力之和作为优化目标，其中在优化过程中每一组配重参数对应的系泊缆张力用PSO-BP神经网络预测值代替，同时以未添加配重块的系泊张力作为约束条件，在工具箱中使用二进制编码、Boltzman选择算子和一致交叉算子，设置迭代寻优次数为300次，得到配重参数最优解。计算未配重情况下和经过遗传算法优化后的各根系泊缆张力，并计算其对应的安全因数，取其差值作为安全因数增量，优化结果如表6所示。

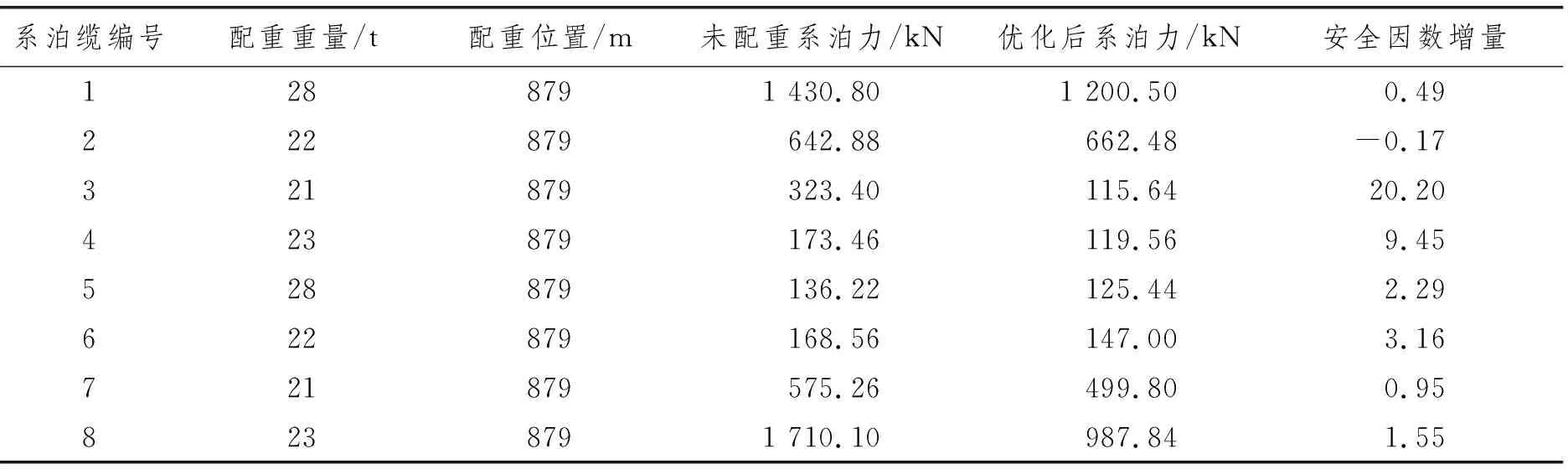
表6 优化结果对比

由表6可知，除2号系泊缆外，其余各根系泊缆的安全因数均增大，整体安全因数增大36.07，2号系泊缆安全因数降低的原因是优化函数为所有系泊缆的安全因数之和，因此可能会出现某几根系泊缆安全因数降低的情况。如果需要单独减小某些系泊缆张力的话，可将优化函数设置为对应的安全因数之和，在此不再举例。由于该优化结果是在整个可选范围内的优化结果，为验证其优越性，取第2.2节中对照组的配重设计数据，通过MOSES软件计算其真实响应，计算8根系泊缆的安全因数之和，与优化结果进行对比，如图3所示，其中，0号为优化结果，1号～10号为对照组结果，可发现优化后的全部系泊缆的安全因数之和均高于对照组，说明此方法确实具有一定的优越性。

图3 优化结果与随机结果对比

3 结 论

(1)在有限数据条件下，以正交试验设计得到的样本数据为基础的PSO-BP神经网络的准确性更高，满足工程实际需要。

(2)在组合缆中钢缆段施加配重块可有效降低系泊缆张力，不同配重参数组合对系泊张力影响不同，在实际系泊系统配重参数初步设计中，可搭建合理的PSO-BP神经网络，借助遗传算法，在给定范围内搜索最优解，得到工程需要的最优配重参数。

(3)不仅是配重初始参数可通过这种方法求解，而且其他系泊参数如缆绳长度、缆绳方位角、缆绳成分占比等大计算量的问题均可通过这种思路初步确定，然后再进行进一步计算。