规则波与不规则波作用下刚架式网箱水动力性能

黄敏敏, 沈 锋, 施兴华, 周 游

(1. 中天科技集团海洋工程有限公司 工程建设部, 江苏 南通 226000;2. 江苏科技大学 船舶与海洋工程学院, 江苏 镇江 212000)

0 引 言

随着世界人口数量的增加和生活水平的提高，人们对优质高蛋白海洋水产品的需求和消费也在不断增加。近年来，网箱的破坏率[1]不断增加，渔民的生命安全和财产安全受到巨大的威胁，为提高网箱的安全可靠度[2]，加强网箱水动力特性的研究具有重要意义。

国内外对于网箱系统已进行大量研究。胡克等[3]对重力式网箱在不规则波和流作用下的水弹性响应进行研究，采用有限元方法建立实尺度网箱模型并对网箱的运动和变形进行分析。胡金鹏等[4]基于海洋工程水动力分析软件OrcaFlex建立网箱数值模型，并通过水池物理模型试验验证了在规则波工况下数值模拟结果的可靠性，进而针对钦州湾20 m水深的重力式网箱系泊系统开展极端海况下的水动力数值研究，极端海况采用百年一遇极端波浪条件。崔勇等[5]研究波浪作用下双层网底鲆鲽网箱水动力特性，根据有限单元法建立波浪作用下双层网底网箱的受力运动模型，通过数值计算求解双层网底的位移和倾角。王绍敏等[6]采用有限元法对NACA0030型翼形网箱在纯浪和浪流共同作用下的容积保持率进行计算，通过对比分析研究网箱容积的变化趋势。KRISTIANSEN等[7]进行浮式网箱在波浪和海流作用下的模型试验，研究网箱模型在波浪和海流中的运动响应。DECEW等[8]通过物理模型试验和数值模拟，研究某新型改进的重力式网箱分别在规则波和不规则波作用下的水动力特性。PURNAWANTI等[9]开展环境载荷作用下海洋养殖场网箱结构静力分析，讨论网衣的变形及网箱结构的静强度。

网箱抗风浪能力的解决是目前网箱养殖存在的主要问题，也是网箱设计的核心技术问题。网箱养殖既要求网箱系统具有足够的强度以抵抗强风浪的袭击，防止鱼类逃逸，又要求构成养殖空间的网箱柔性网衣可在各种海流条件下变形尽可能小，以保持必需的养殖空间，以免导致鱼类的摩擦损伤和窒息死亡。刚架式网箱的刚架具有足够的强度和刚度，具有承受较大载荷的能力，安全性高，因此需要对刚架式网箱进行水动力性能分析，计算各连接系统的受力及网箱的容积剩余率，在网箱的实际应用中具有较好的参考价值。

1 网箱模型

1.1 运动方程

基本的运动方程是在BREBBIA等[10]的建议下在Morison方程的基础上进行修改的，公式为

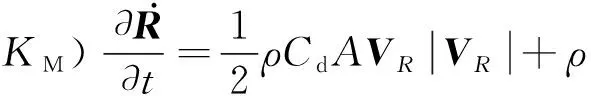
(1)

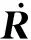
为方便计算，式(1)中等号右边第一项和第二项用FD和FI表示，分别代表拖曳力和惯性力。左边项可视为包括流体附加质量在内的总质量，流体附加质量与结构运动一起加速。然而要将式(1)应用到网箱系统中，还应该包括浮力FB、重力FW和网线张力FT[12]。因此，适合用来表示网箱系统的一般运动方程为

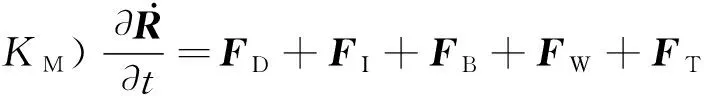
(2)

1.2 网箱数值模型

表1为刚架式网箱所需的计算参数，该模型模拟水深设为100 m，中心岛与浮架之间用36块板连接，其中浮架为图1(b)中最外圈的圆环，板长为30 m，两板之间夹角为10°。网箱模型为4点锚碇方式，锚泊点距网箱中心水平距离为70 m。

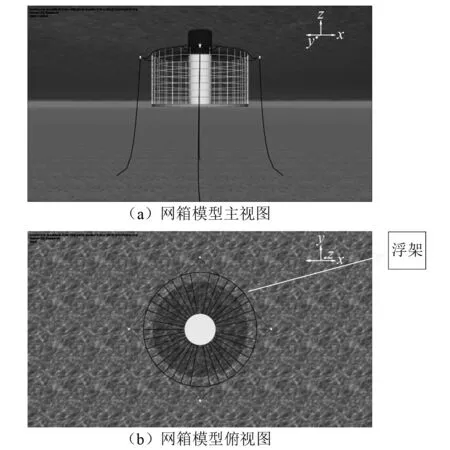
图1 刚架式网箱模型

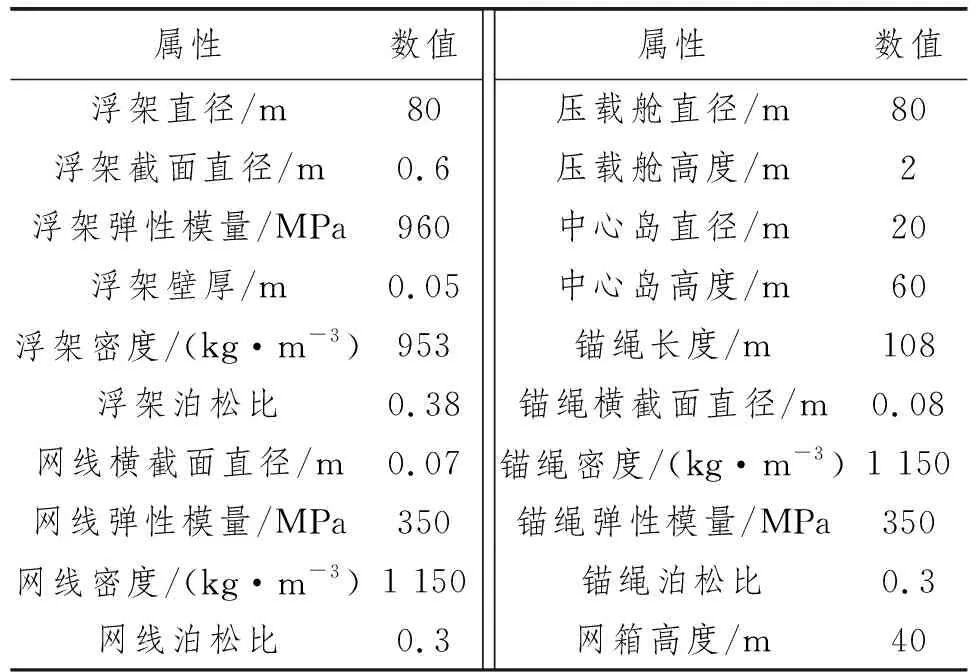
表1 网箱参数

刚架式网箱模型如图1所示。

在数值模拟中，定义不同的波浪、水流方向，4根锚绳分别为系泊缆3、系泊缆 6、系泊缆 9、系泊缆 12，如图2所示。

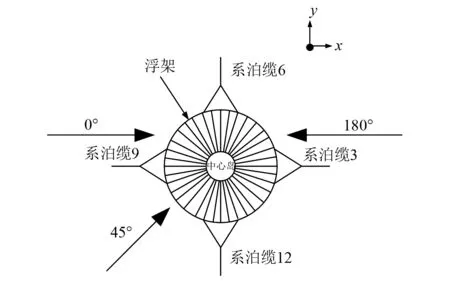
图2 波流方向示例

2 波浪作用下计算工况选取

与其他海洋工程结构物类似，波浪作用下刚架式网箱的受力和运动计算需要根据实际海域情况[11-13]采用合理的波浪理论。选用规则波(Airy波)和不规则波(JONSWAP波)两种不同的波，研究其对网箱受力、运动变形的影响。刚架式网箱布置在福建海域，福建海域的波浪周期为4.2～9.8 s，年平均波高约1.3 m。因此，选取的浪向为0°，对波高H=1.3 m，周期T=6、7、8 s的工况进行数值模拟。表2为波浪作用下的工况。

表2 纯波浪工况

3 刚架式网箱水动力数值模拟

3.1 浮架与网衣连接点受力分析

刚架式网箱的浮架为刚性材料，而网衣为柔性材料，研究其连接点的受力特点极为重要。选取水流方向为0°的工况：与迎流面系泊缆 9最近的迎流面网衣记为前接网衣，该网衣与浮架的连接点记为前网衣连接点；与背流面系泊缆3最近的背流面网衣记为后网衣，该网衣与浮架的连接点记为后网衣连接点。图3为在规则波作用下，网箱网衣在波高H=1.3 m，周期T=6 s、7 s、8 s的前网衣连接点和后网衣连接点有效张力曲线。

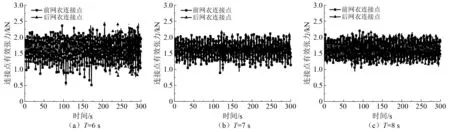
图3 规则波作用下连接点有效张力

由图3可知，浮架与网衣连接点的有效张力在初始阶段迅速增大，逐渐在一个受力区间内波动。在规则波作用下，在同一周期内，前网衣连接点的最大有效张力比后网衣连接点的最大有效张力大，但两者相差很小。当周期T=6 s时，两者相差0.02 kN；当周期T=7 s时，两者相差0.06 kN；当周期T=8 s时，两者相差0.02 kN。

图4为在不规则波作用下网箱网衣在波高H=1.3 m，周期T=6 s、7 s、8 s的前网衣连接点和后网衣连接点有效张力曲线。

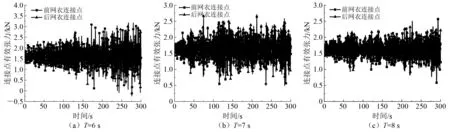
图4 不规则波作用下连接点有效张力

由图4可知，在不规则波作用下，在同一周期内，前网衣连接点的最大有效张力比后网衣连接点的最大有效张力大，但两者相差很小。当周期T=6 s时，两者相差0.01 kN；当周期T=7 s时，两者相差0.05 kN；当周期T=8 s时，两者相差0.07 kN。

图5为在规则波和不规则波作用下连接点最大有效张力的对比。由图5可知，在同一周期下，网衣与浮架连接点的有效张力基本相同，由于网衣的遮蔽效应，前网衣的受力大于后网衣。在同一周期内，在不规则波作用下连接点最大有效张力大于在规则波作用下连接点最大有效张力。当周期T=6 s时，两者相差0.68 kN；当周期T=7 s时，两者相差0.50 kN；当周期T=8 s时，两者相差0.37 kN。周期越大，两者相差越小。在不规则波浪作用下，同一波高，周期越大，连接点的最大有效张力越小。

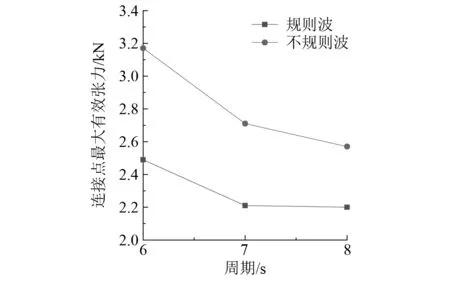
图5 连接点最大有效张力对比

3.2 锚绳力分析

当浪向为0°时，系泊缆9为迎浪侧锚绳。研究规则波与不规则波作用下迎浪侧系泊缆9的锚绳受力情况，如图6和图7所示。

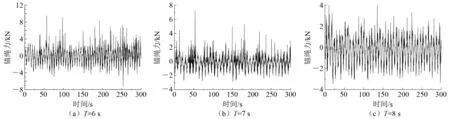
图6 规则波作用下锚绳力

图7 不规则波作用下锚绳力

由图6和图7可知，在规则波与不规则波作用下迎浪侧锚绳受力波动幅度随周期的增大而减小。当周期T=6 s时，规则波的最大锚绳力为9.50 kN，不规则波的最大锚绳力为18.83 kN；当周期T=7 s时，规则波的最大锚绳力为7.63 kN，不规则波的最大锚绳力为12.42 kN；当周期T=8 s时，规则波的最大锚绳力为4.08 kN，不规则波的最大锚绳力为8.54 kN。

图8为在规则波和不规则波作用下迎浪侧锚绳最大锚绳力对比。由图8可知，在同一周期下，在不规则波作用下迎浪侧锚绳的最大锚绳力大于规则波作用下迎浪侧锚绳的最大锚绳力。当周期T=6 s时，在不规则波作用下迎浪侧锚绳的最大锚绳力约为在规则波作用下迎浪侧锚绳的最大锚绳力的1.98倍，两者相差9.33 kN；当周期T=7 s时，在不规则波作用下迎浪侧锚绳的最大锚绳力约为在规则波作用下迎浪侧锚绳的最大锚绳力的1.62倍，两者相差4.79 kN；当周期T=8 s时，在不规则波作用下迎浪侧锚绳的最大锚绳力约为在规则波作用下迎浪侧锚绳的最大锚绳力的2.09倍，两者相差4.46 kN。周期越大，两者相差越小。在同一波高下，周期越大，迎浪侧锚绳的最大锚绳力越小。由此可见波浪类型是影响网箱锚绳力的重要因素。

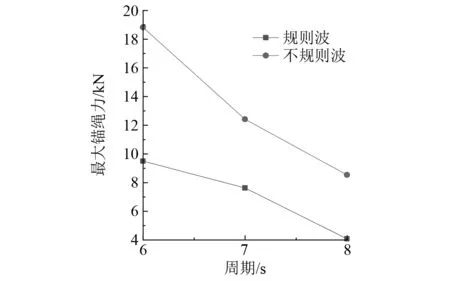
图8 最大锚绳力对比

3.3 网箱容积剩余率

由于网箱在波浪作用下一直浮动，因此给出网箱容积剩余率变化的时历曲线，如图9所示。

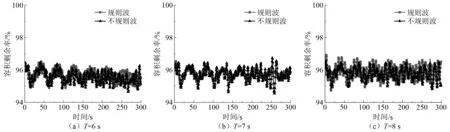
图9 波浪作用下网箱容积剩余率

由图9可知，网箱的容积在初始时刻迅速减小，在规则波作用下经历了一段时间的不稳定波动后会在一个固定区间内稳定波动，而在不规则波作用下网箱容积剩余率峰值出现随机状况，时大时小，但整体仍处于一个较大的区间内。在规则波作用下，当周期T=6 s、7 s、8 s时，网箱容积剩余率的波动区间分别为94.89%～96.53%、95.21%～96.29%、94.94%～96.78%。在不规则波作用下，当周期T=6 s、7 s、8 s时，网箱容积剩余率的波动区间分别为94.64%～96.47%、94.55%～96.76%、94.81%～96.68%。

图10为波浪作用下网箱最小容积剩余率对比和网箱最大容积剩余率对比。

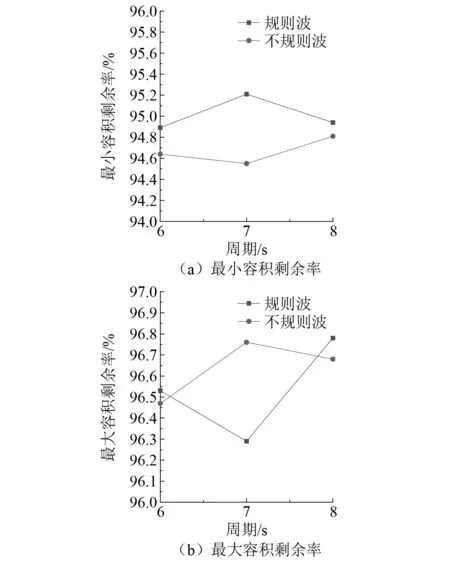
图10 波浪作用下网箱容积剩余率对比

由图10可知，在同一周期内，在规则波与不规则波作用下的网箱最大和最小容积剩余率相差较大：当周期T=6 s时，最大容积剩余率相差0.06%，最小容积剩余率相差0.25%；当周期T=7 s时，最大容积剩余率相差0.48%，最小容积剩余率相差0.66%；当周期T=8 s时，最大容积剩余率相差0.10%，最小容积剩余率相差0.13%。在不规则波条件下网箱的变形更严重，可提供的最小养殖体积比在规则波浪条件下稍微小一些。

4 结 论

采用OrcaFlex软件，考虑不同的波浪类型，对刚架式网箱的锚绳受力、浮架与网衣连接点受力和网箱容积剩余率进行数值模拟分析，得到结论如下：在同一周期下，网衣与浮架连接点的有效张力基本一致；在同一波高下，周期越大，连接点的最大有效张力越小，在规则波与不规则波作用下迎浪侧锚绳受力波动幅度随周期的增大而减小；在同一周期内，在不规则波作用下迎浪侧锚绳的最大锚绳力大于在规则波作用下迎浪侧锚绳的最大锚绳力；在同一波高下，周期越大，迎浪侧锚绳的最大锚绳力越小；在同一周期内，在规则波与不规则波作用下的网箱最大容积剩余率相近，最小容积剩余率相差较大，两者作用下的网箱容积剩余率相差较大，但在不规则波条件下网箱的变形更严重，可提供的最小养殖体积比在规则波条件下稍微小一些。