遮蔽效应下双平面网衣和圆形网衣的水动力性能
张 婧,华福永,周 游,施兴华
(江苏科技大学船舶与海洋工程学院,江苏镇江 212100)
0 引 言
近年来,随着海洋工程领域有关技术和设备的不断发展,海水养殖业不断从近海走向远海、深海,网渔具和网箱在海洋渔业生产中的应用越来越广泛。网箱上的网衣作为其主要构件,对整体设备的受力起主导作用。与其他海洋结构物相同,网衣及由网衣构成的渔具和渔业设施在海洋中会承受风、浪和流等环境因素的影响。网衣的水动力研究[1-3]涉及多个学科,包括数学、物理学和流体力学等,研究手段非常复杂。
目前有关网衣类型对流场特性和水动力性能的影响的研究尚未十分成熟。在国外方面:PATURSSON[4]提出采用多孔介质模型模拟平面网衣,研究了水流经过网衣作用之后,其速度衰减的规律;JOHANSSON等[5]测量了在挪威西海岸区域和在峡湾内布置的组合式网箱周围的流速,分析了网箱的流速衰减情况,同时对网箱周围的盐度、温度和溶解氧进行了测量;WERGELAND[6]研究了网箱配重底圈的涡激振动问题,分析了组合式网箱在波浪作用下的锚绳受力特性和在波流联合作用下的体积衰减问题;PASCAL 等[7]采用声学多普勒流速剖面仪和声学多普勒流速仪(Acoustic Doppler Velocimeter,ADV)测量了水流衰减情况,研究了水流经过圆形网箱的作用之后,其速度衰减的规律。在国内方面:刘超等[8]设计了4 种不同网目形状和不同网目大小的网箱模型,采用ADV和粒子图像测速(Particle Image Velocimetry,PIV)技术对网箱系统内外的流速和流场变化进行了测定,研究了圆形重力式网箱在动态流场中的水动力学性能,同时获得了网箱系统内部与周围的流场分布及流速变化规律;林为付[9]通过开展模拟试验研究了与网箱动态响应有关的参数,分析了圆形养殖网箱结构及流场中网箱的动态响应情况;李鹏等[10]基于计算流体力学(Computational Fluid Dynamics,CFD)方法对小尺度平面无结金属网衣进行了数值模拟试验,研究了其在均匀流作用下的水动力性能和网衣周围的流场分布,得出了阻力系数和速度场分布随雷诺数、网衣的攻角、网衣密实度和网眼形状的变化趋势。
在水流作用下,网衣受力会使网箱发生变形,一旦水流速度过大,不仅会导致网箱的容积大幅度减小,而且会影响网箱内外水体的交换,降低养殖生物的存活率。基于上述情况,本文通过STARCCM +软件进行数值仿真,对比分析双平面网衣与圆形网衣在流场中不同流速下的拖曳力和阻力系数的变化规律,为海洋网箱设计和流场特性分析提供参考。
1 数值模型
1.1 网衣数值模型
基于三维建模软件SolidWorks建立双平面网衣和圆形网衣2 种网衣模型,具体参数见表1。为着重研究网衣在遮蔽效应下的受力情况,将方形网箱上的网衣简化为同一方向上的前后2 个受力平面,将圆形网箱外网衣简化为水平流域上的受力面。双平面网衣模型参照方形网箱模型及其不相邻的2 个平面,双网衣之间的距离为0.8 m。圆形网衣模型参照圆形网箱的形状,为确保其面积与平面网衣的投影面积相同,取圆形网衣的直径为0.8 m,高为0.4 m,其他条件与平面网衣基本保持一致。

表1 网衣参数
1.2 网衣受力计算
网衣是多孔状结构,一般采用水池试验或数值计算的方法对其水动力性能进行研究;计算网衣流体载荷的方法主要有多孔介质法、集中质量法、屏模型和莫里森公式等。下面采用莫里森公式对2 种网衣进行数值计算,包括网衣受力面改进计算和水动力系数选取,在此基础上建立流场域,设置数值模拟的边界条件。
1.2.1 网衣受力相似条件
对于网衣而言,控制受力的动力因素主要是水流阻力、网衣在水中的重量和浮力,其中网衣所受水流阻力与网衣的垂直投影面积有关,这样从相似准则的角度来说,只要满足主要动力因素的相似要求即可。一般而言,网衣受力相似条件应遵循几何相似、水阻力相似、重量和浮力相似。本文在已有研究的基础上,提出以下计算改进方法:在保持网衣总尺度几何相似的前提下,确保网衣受力总面积几何相似,增大网线直径和网目尺寸,减小模型网衣对水流流态的改变,保证水动力相似并使网衣模型可行。
在计算网衣受力时,可采用流体动力的一般公式(Morison方程),即
式(1)中:F为网衣的水阻力;A为网衣与水流垂直时的网线投影面积;CD为水阻力系数;ux为流速;ρ为流体密度。当考虑有结节网衣时,结节直径按3.14 乘以目脚直径计算,单位缩结面积的网线投影面积为
若忽略式(2)右端的第二项,并取整个网衣的缩结面积为S,则式(2)可近似表示为
日本学者田内[11]曾考虑各种冲角,并对网衣进行阻力测试,得到经验公式
式(2)~式(4)中:a为目脚;θ为冲角;S为网衣的大尺度面积。当θ =90°时,式(4)可简化为
1.2.2 网衣的水动力系数选取
增大网线直径和网目尺寸会导致网衣体积增大,产生的浮力远大于改进之前的浮力,因此为协调重力与浮力,需调整网衣的水动力系数。在纯水流情况下,网衣的水动力系数CD与雷诺数Ren有关,将水阻力系数与雷诺数的关系总结成函数关系,有
式(6)~式(8)中:CDn为速度力的切向速度力系数;CDt为速度力的法向速度力系数;μ 为液体的运动黏性系数;ρ为流体密度;vRn为水流相对目脚的流速;D为网目目脚直径。液体的运动黏性系数与温度有关,这里取温度为20 ℃时的值,即1.35 ×10-6m2/s。为方便计算,将速度力系数设定为常数,由于CDn在1.1 附近小范围波动,CDt在0.14 附近小范围波动,因此分别取CDn和CDt的值为1.1 和0.14。
1.3 控制方程
流体流动连续性方程[11]的微分形式为
对于密度为常数的不可压缩均质流体,式(10)可进一步简化为
式(10)和式(11)中:ρ为流体的密度;t为时间;u、v和w分别为速度矢量在x方向、y方向和z方向的分量。
2 网格收敛性验证及网格划分
2.1 网格收敛性验证
设定网衣数值模拟的边界条件,对全流域网格的基础尺寸进行调整,划分出数量不同的3 套网格,由此对网格的收敛性进行验证。3 套网格的基础尺寸设置及网格总数见表2。

表2 3 套网格的基础尺寸设置及网格总数
3 套网格的截图见图1。从图1 中可看出:随着网格数量的增加,网衣表面和计算域的网格划分越来越均匀,同时两者交界处的过渡越来越自然;随着网格数量的增加,计算的负担越来越大。因此,为选择合适的网格尺寸,以进口速度0.5 m/s为例对3 套网格进行后网衣阻力计算,分别对比达到稳定所需迭代步数和阻力值。

图1 3套网格的截图
图2 为3 套网格的迭代步数与阻力的关系曲线对比。从迭代曲线上看,3 套网格的迭代步数到400 步时就已趋于平稳;从运算结果上看,3 套网格的受力值相差不到0.5 N,相对误差较小,在6%以内。综上所述,考虑到网格过多会影响计算机的运算速度,后续水动力数值模拟分析均采用基础尺寸为250 mm 的网格进行有关计算。
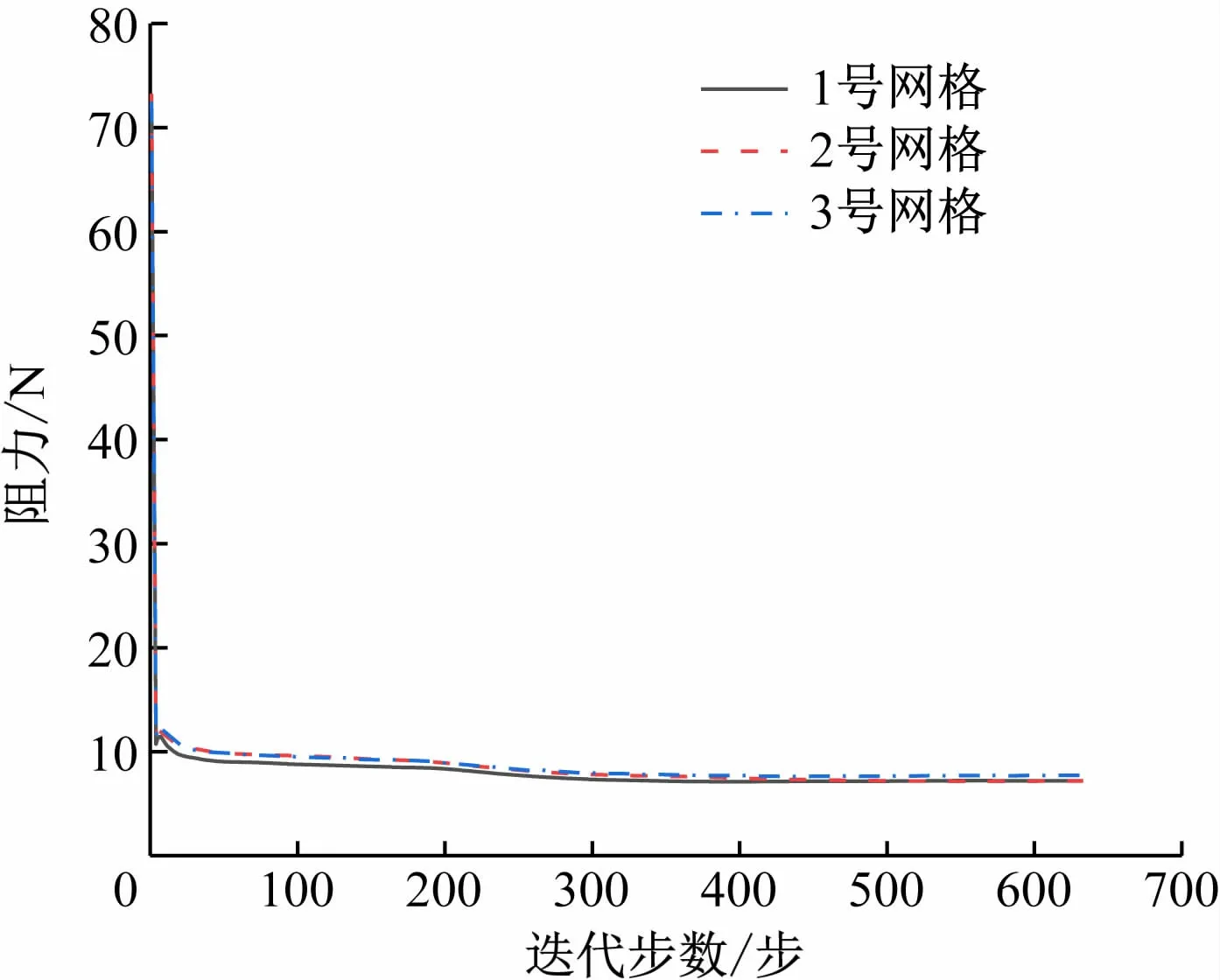
图2 3套网格的迭代步数与阻力的关系曲线对比
2.2 网格划分
网格是几何域的离散表示,也是计算模型前处理的重要组成部分,因此本文建立计算域,并对其进行网格划分。将网衣置于尺寸为5.0 m×2.0 m×0.6 m 的计算域内,网格生成器为表面重构和切割体网格单元生成器,网格基础尺寸为0.25 m,最小表面尺寸为基础尺寸的10%(即0.025 m)。在计算域内布置尺寸为5.0 m×2.0 m×0.2 m的自由液面,为对自由液面网格进行加密,设置网格各向异性,X轴和Y轴方向的网格大小相当于基础尺寸的20%(为0.050 0 m),Z轴方向的网格大小相当于基础尺寸的5%(为0.012 5 m)。
3 网衣三维数值模拟
3.1 流场模拟
选取入射水流速度分别为0.5 m/s、1.0 m/s、1.5 m/s和2.0 m/s,对网衣的整体流场进行数值模拟,入射角为90°,模拟时间为20 s,隐式不定常时间为0.008 s,最大内部迭代次数为10 次。着重分析2 种网衣在水平流场中的变化。图3 和图4 为2 m/s流速下2 种网衣的水平流场分布。
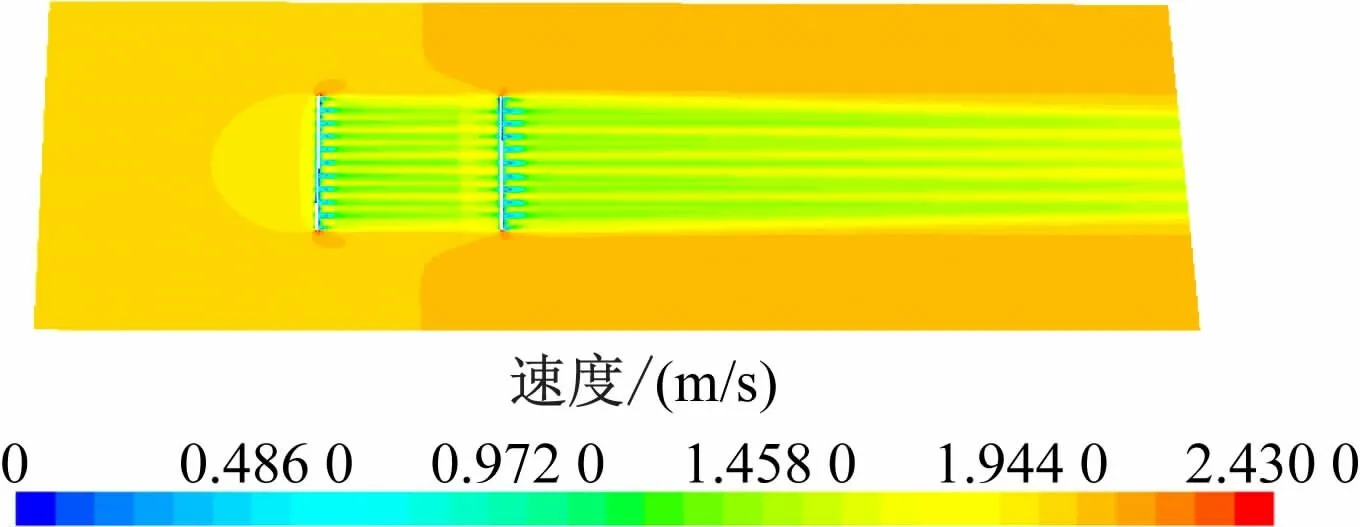
图3 2 m/s流速下双平面网衣的水平流场分布
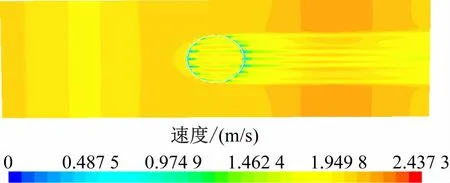
图4 2 m/s流速下圆形网衣的水平流场分布
从图3 和图4 中可看出:由于网衣的遮蔽效应,水流经过2 种网衣时均会产生阻流,在网衣之间均存在明显的流速衰减;当水流穿过2 层网衣之后,在后网衣之后的区域流速衰减幅度更大,在图3 中靠近后网衣的区域以及图4 中靠近两侧网衣的区域存在一段很短的压力真空带;随着与网衣距离的增大,流速衰减区域的宽度有逐渐减小的趋势;衰减区域两侧及底部的水流速度,随着与网衣距离的增加而增大;由于网衣的开孔率较大,当水流穿过网衣时,其流动方向并没有发生明显的变化。
3.2 网衣水平拖曳力分析
进一步对4 种流速场下2 种网衣的受力变化进行对比分析。4 种流速下双平面网衣和圆形网衣的受力曲线分别见图5 和图6。

图5 4种流速下双平面网衣的受力曲线

图6 圆形网衣受力曲线
由图5 可知,在流场中,双平面网衣的水平拖曳力在初始阶段存在一个极大值,从极大值开始受力迅速减小,随后迅速增大,最后达到稳态,稳态受力结果见表3。在同一流速下,前网衣达到稳态的时间比后网衣早,前网衣受到的水平拖曳力比后网衣大。对比稳态受力结果可知,随着流速的增加,网衣的水平拖曳力增大,前网衣与后网衣的受力结果相差越来越大。图7 为2 种网衣在稳态下的水平拖曳力对比。由图7 可知,圆形网衣在流场中的受力变化与双平面网衣相似,当流速增加时,网衣的水平拖曳力增大。
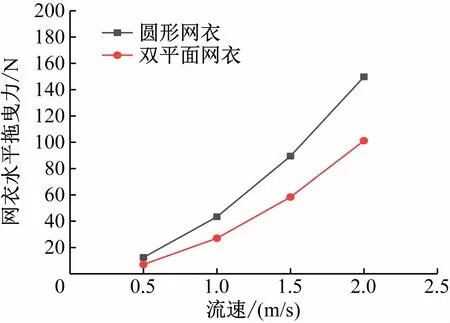
图7 2种网衣在稳态下的水平拖曳力对比

表3 双平面网衣稳态受力结果
由此可知,圆形网衣的受力始终比双平面网衣的大,两者在流速为0.5 m/s时相差最小,为5.3 N,在流速为2 m/s时相差最大,为48.6 N。圆形网衣与双平面网衣的水平拖曳力有相同的变化趋势,均随着流速的增加而增大。
3.3 阻力系数分析
根据遮蔽效应下的流速衰减和网衣受力情况,计算不同流速下网衣的阻力系数。4 种流速下双平面网衣和圆形网衣的阻力系数随时间的变化曲线分别见图8 和图9。

图8 双平面网衣的阻力系数随时间的变化曲线
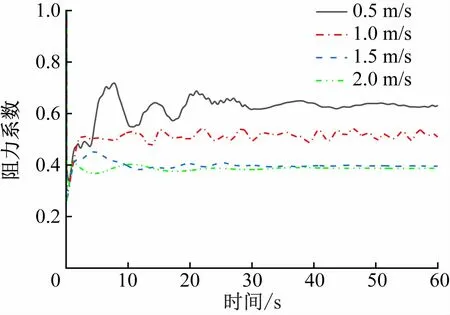
图9 圆形网衣的阻力系数随时间的变化曲线
由图8 可知:在流场中,双平面网衣的阻力系数在初始阶段迅速减小,随后迅速增加,最后达到稳态;在同一流速下,前网衣达到稳态的时间比后网衣早。整体上看,前网衣的阻力系数比后网衣的略大;当流速为1.0 m/s时,前网衣的阻力系数比后网的略小,但因该流速下两者的结果基本一致,对网衣的影响较小,可忽略不计。对比稳定状态下前后网衣的阻力系数值发现,前网衣与后网衣的阻力系数相近,当流速为1.5 m/s时,两者的阻力系数仅相差0.004,当流速增加时,双平面网衣的阻力系数反而减小。
图10 为2 种网衣的阻力系数随流速的变化曲线对比。由图10 可知:稳态下圆形网衣与双平面网衣的阻力系数相差不大,且随着流速的增加,两者的数值越来越接近;当流速为0.5 m/s时,2 种网衣的阻力系数相差最大,为0.066;当流速为2.0 m/s时,2 种网衣的阻力系数仅相差0.008。与双平面网衣一样,当流速增加时,圆形网衣的阻力系数反而减小。
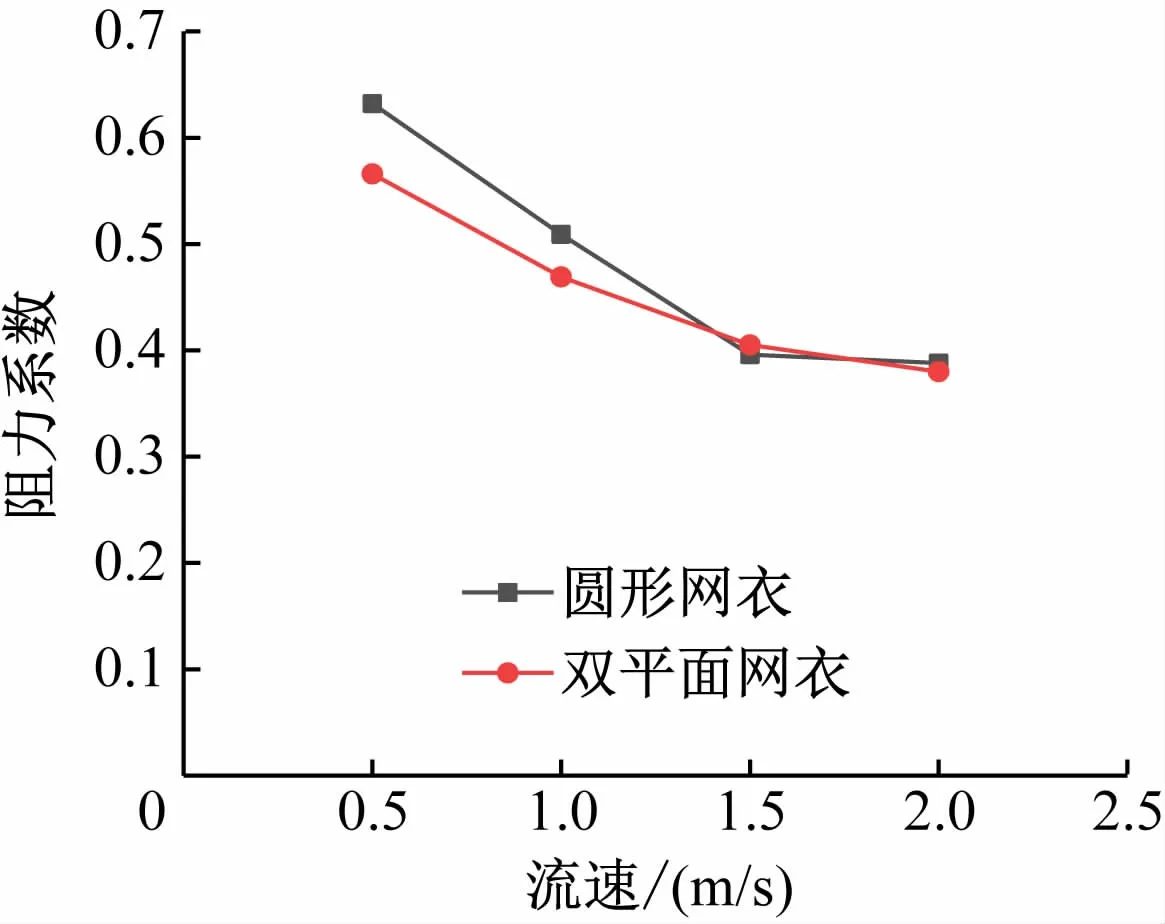
图10 2种网衣的阻力系数随流速的变化曲线对比
4 结 语
本文运用STARCCM +软件对2 种网衣进行数值仿真模拟,建立合适的流场域验证网格的收敛性。通过分析水流经过网衣之后的流速衰减情况,计算网衣的受力和阻力系数,主要得到以下结论:
1)由于网衣的遮蔽效应,在网内和网后存在明显的流速衰减,在靠近网衣的区域可清晰地看见一段很短的真空带,随后流速增加,逐渐达到稳态。在水平流场中,随着与网衣距离的增大,在衰减区域两侧水流的速度相应增加。
2)网衣网前流速均大于网内和网后流速,网内流速大于网后流速,各流速下网内的流速衰减系数均大于网后的流速衰减系数,且都在一定范围内。
3)在流场中,网衣的水平拖曳力和阻力系数在初始阶段存在一个极大值,从极大值开始受力迅速减小,随后迅速增加,最后达到稳态。当流速增加时,网衣的水平拖曳力增大,阻力系数减小。
4)圆形网衣的受力始终比双平面网衣的大,随着流速的增加,两者具有相同的变化趋势;稳态下圆形网衣与双平面网衣的阻力系数相差不大,且随着流速的增加,两者的数值趋近。

