高峰时段郊区线考虑列车容量约束的停站方案优化方法研究

2023-10-30 11:39张惠茹豆飞魏运刘洁宁尧

交通运输系统工程与信息 2023年5期

张惠茹，豆飞*，魏运，刘洁，宁尧

(1.北京市地铁运营有限公司，北京 100044；2.地铁运营安全保障技术北京市重点实验室，北京 100044)

0 引言

凭借大容量、安全可靠及快速便捷的优势，城市轨道交通已成为满足中心城区交通以及郊区通勤和通学客流出行需求的重要交通方式。截至2022 年底，我国有26 个城市线网规模达到100 km及以上，其中，上海(936.17 km)和北京(868.37 km)已形成超大线网规模[1]。由于职住分离现象，大城市郊区线路的客流往往具有明显的长距离出行和时空分布不均衡特征，在客运高峰时段，部分车站客流量较小，而部分车站由于过高的列车满载率导致乘客滞留站台。针对上述线路，站站停方案将造成乘客出行时间过长，以及列车满载率与上车客流需求匹配度不足的问题[2]，组织开行不同站停方式的列车是一种有效的手段。

目前，国内外学者针对列车停站方案已经开展了相关研究。范马宁[3]认为在共线共轨运行模式下，为更加充分利用线路通过能力，应当组织快车越行慢车，但是，也可能导致慢车在越行站停站时间增加的问题。于德涌[4]通过分析开行快车对线路通过能力造成损失的情况，提出由于快车越行慢车需要车站具备越行条件，因此，快车不越行的运营模式是我国既有城市轨道交通线路开行快慢车的首选方式。王琳[5]将快车停站方案和快慢车发车频次作为决策变量，以最小化乘客旅行时间和运营成本为目标，采用改进遗传-模拟退火算法得到快慢车组合方案。张化难[6]旨在最大化乘客总体出行节省时间，建立0-1停站方案模型，并采用分支定界法得到最佳停站方案。JAMILI 等[7]以总旅行时间最小为优化目标，采用基于跳停方案分解和模拟退火两种算法进行求解，案例说明，后者在求解大规模问题时效果更优。孙元广等[8]以最小化乘客出行时间和列车周转时间为目标，同时，考虑乘客在给定快慢车方案条件下的换乘行为，构建双层规划模型并采用粒子群算法求解。LI等[9]以降低乘客出行时间为目标，建立混合整数非线性模型，运用分支定界算法实现停站方案与列车时刻表的协同优化。也有学者在优化停站方案时考虑了乘客滞留现象。陈维亚等[10]在设定快慢车开行比例以及慢车和快车配组开行基础上，优化包括滞留乘客在内的乘客在站总等待时间和乘客在车总旅行时间。吴文祥等[11]在最小化系统乘客总等待时间的目标中引入最大站台乘客人数作为惩罚，构建列车灵活跳站运行模型。针对高峰时段采用站站停方案，将导致乘客在车站乘坐不同满载率列车甚至滞留车站的问题，SHANG等[12]基于公平性原则，实现所有乘客的公平分配并得到最优跳停方案。

综上，对于列车停站方案优化问题，最小化所有乘客总出行时间是核心目标，同时，由于问题的解空间随着车站和列车数量的增加而急剧增长，智能优化算法被广泛应用。总的来说，学者们对该问题已经开展了较为丰富的研究，但是仍存在一些不足：部分研究只考虑因快车跨站运行造成的乘客滞留，而未考虑高峰时期超高的列车载客量导致乘客滞留的情况；部分研究基于设定的快慢车开行比例或者快车跳停车站，限制了停站方案的多样化；部分研究未考虑运输组织的可操作性，计算的跳停方式过于复杂且无序；此外，大多数研究未考虑多样化停站方案造成的列车发车间隔不均衡的问题。因此，针对具有长距离出行和时空分布不均衡客流特征的郊区线路，在客运高峰时段，本文考虑列车容量约束，以最小化包括候车时间和旅行时间在内的乘客总出行成本为目标，建立优化模型，并设计一种基于灾变思想的改进遗传算法，实现考虑列车容量约束的列车停站方案优化。此外，通过定义运行图发车间隔均衡性评价指标以更好地服务乘客出行，提高运行图鲁棒性。

1 问题描述

城市轨道交通的郊区线路通常延伸到城市边缘，连接着城市中心区域与周边郊区地区。郊区线路客流往往呈现出长距离及长时间乘车出行的特性，根据分析北京地铁主要线路的平均运距和平均乘车时间可知：房山线、15 号线和昌平线等郊区线路的平均运距以及平均乘车时间均远高于2 号线和9 号线等中心区域线路。北京地铁部分线路平均运距和平均乘车时间如图1所示。

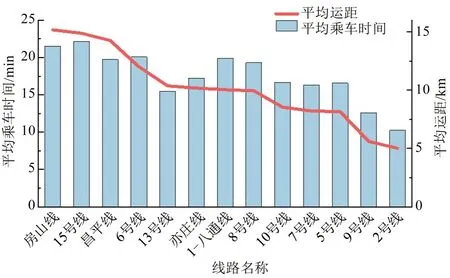
图1 北京地铁部分线路的平均运距和平均乘车时间Fig.1 Schematic diagram of average travel distance andaverage travel time on Beijing Subway lines

郊区线客流在工作日的高峰时段往往非常集中，早高峰时段以进城方向为主，晚高峰则相反。以北京地铁典型郊区线房山线为例，分析房山线某工作日各区间断面客流量可知：在早晚高峰时段，列车在上下行方向以及同方向不同区间的客流分布极其不均衡如图2所示。其中，上行方向从始发区间开始依次排序为区间1～区间15，下行方向依次排序为区间16～区间30。

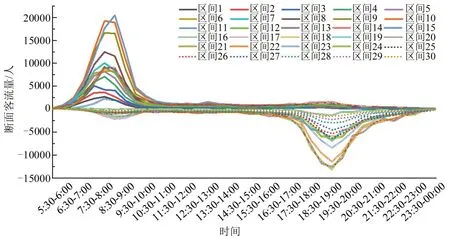
图2 典型郊区线路全日所有区间断面客流量Fig.2 Section passenger flow volume on a typical suburban line during whole day

针对车站总数为N的城市轨道交通郊区线路，在高峰时段T内采用多样化停站方案，则列车以不同满载率运行，如图3所示。列车1～列车3分别采用停站方案1～方案3。其中，列车1 采用站站停模式，在车站3 达到最大满载率，即站台乘客无法全部上车，造成乘客留乘；列车1 在后续多个车站仍将因最大载客量限制导致乘客滞留站台。列车2和列车3在某些车站通过不停车，一方面，考虑大部分通勤乘客出行距离较长，通过跳站的方式可以有效缩短该时段乘客的出行时间；另一方面，考虑各车站客流分布不均衡的现状，跳停某些客流量相对较小的车站，在满载率已经很高的条件下跳停某些上车客流量远大于下车客流量的车站，将节省车上乘客时间，并且减少低效停站，即虽然停站但受列车满载率限制乘客无法上车的情况。多样化的停站方案可以更加准确地匹配客流量与列车满载率，但是，过于复杂且无序的方案也会降低实际运输组织的可操作性，造成乘客出行困难。因此，停站方案应兼顾线路能力利用和乘客服务水平。

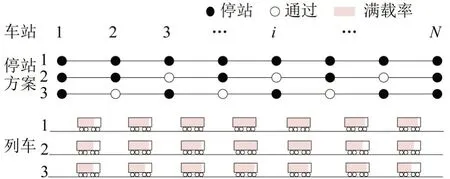
图3 城市轨道交通车站、列车和停站方案Fig.3 A schematic diagram of stations,trains and stopping patterns for urban train transit line

相邻列车采取不同停站方式时，将一定程度影响列车运行图的均衡性[13]。以A1、B1 和C1，以及A2、B2 和C2 的2 组列车为例，由于列车B1 跳停了部分车站，导致第1组相邻列车发车间隔的均衡性变差，即相邻列车在同一车站的发车间隔差距变大，到达该站的乘客等候相邻列车的时间偏差变大，进而影响列车运行图鲁棒性。相邻列车发车间隔偏差如图4所示。

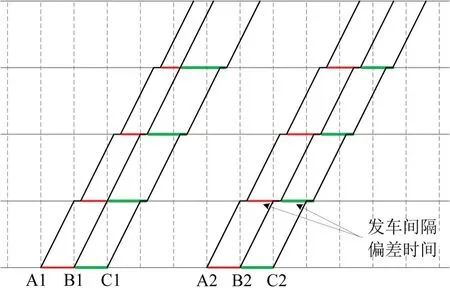
图4 相邻列车发车间隔偏差Fig.4 A schematic diagram of deviation between departure intervals of adjacent trains

综上，研究高峰时段郊区线路考虑列车容量约束的停站方案，同时，考虑生成运行图发车间隔均衡性，对匹配运营企业运能与乘客出行需求和提升服务效率意义重大。

2 模型建立

2.1 假设与变量

为方便问题描述，本文建立在以下假设基础上：①在研究时段T内，各OD 对间的客流均匀到达；②列车在始发车站等间隔发车；③开行快慢车过程中，列车运行顺序不改变；④乘客采用一站直达的方式，不考虑快慢车之间的换乘，当前到站列车仍有载客余量且可到达客流目的车站时，乘客即上车，不考虑客流继续等待后续列车的情况。本文涉及的主要变量及参数如表1所示。

表1 主要参数及变量Table 1 Key parameters and variables

2.2 客流计算

(1)上车乘客数量

当乘客需求量超过列车最大载客量时，上车乘客数量受满载率限制；否则，所有乘客均可上车。根据列车载客情况的不同，列车k在车站i的上车乘客数量为

(2)下车乘客数量

假定列车k到达车站m的车内乘客按照后续车站i吸引客流总量的相对比例下车，即

式中：N为车站总数；为乘坐列车k从车站m到车站i的下车乘客数，则列车k到达车站i下车总乘客数为

始发站到达载客量为0，即∀k，=0。

(3)列车离站载客数量

终到站离站载客量为0，即∀k，=0。

(4)留乘乘客数量

当且仅当乘客需求量超过列车最大载客量时有乘客滞留，因此

终到站无滞留乘客，即∀k,=0。

(5)进站/换乘乘客数量

根据假设，研究时段T内各OD对间的客流qi,j均匀到达，则列车k和列车k-1 发车间隔内车站i到达车站j的乘客速率vi,j,k为

列车k和列车k-1 在车站i发车间隔hi,k的进站/换乘客流量为

终到站无进站或换乘乘客，即∀k，

(6)候车乘客数量

列车k到达车站j时的候车乘客包括两部分，列车k-1 的留乘乘客和两列车之间的进站/换乘乘客，则

(7)乘客候车时间计算

列车k到达车站i时，留乘乘客的等候时间为hi,k，假定乘客到达车站服从均匀分布，则进站/换乘乘客的等候时间为hi,k2，则

终到站无乘客候车，即∀k，

(8)乘客旅行时间计算

旅行时间包括到站未下车乘客在车站的站停时间，离站后车内乘客在区间的运行时间和启停附加时分，则

终到站旅行时间为0，即∀k，

2.3 目标函数

以乘客总出行成本最小为优化目标，则

式中：Z为线路所有乘客总出行成本。

2.4 约束条件

(1)特殊车站停站约束

所有列车在始发站、终到站以及部分客流量较大的关键车站需要停车。

式中：Ω*为客流量较大的关键车站集合。

(2)追踪间隔约束

追踪间隔时间指同方向相邻列车在运行过程中保证互不干扰的最小间隔时间。由于快慢列车之间存在技术速度差，因此，列车k-1 和列车k之间的发车间隔满足

其中，ai,k和di,k为

(3)列车连续跨站数量约束

式中：Mt,max为列车最多连续跨站数量的上限值。

(4)车站连续跳停列车数量约束

式中：Ms,max为车站最多允许连续跳停列车数量的上限值。

(5)车站可达约束

式中：Mnum为站停方式数量，且Mnum＞Ms,max；Maccess为可达性下限值。考虑站停方式过多不利于车站运输组织工作，也影响旅客正确快速乘车，因此，约束站停数量，后续列车重复采用列车k～k+Mnum站停方式。

(6)站停方式约束

式中：Ψ(k)为列车k在所有车站停站标识的顺序排列，Ψ(k)=(x1,k,x2,k,…) ；K′为采取不同站停方式的列车集合。

3 求解算法

本问题具有约束数量多和耦合关系强的特点，问题的复杂程度随着线路车站数量和列车数量的增加呈指数上升趋势。遗传算法(Genetic Algorithm,GA)具有较强的全局搜索能力，优化结果不依赖于初始条件，但是，容易陷入“早熟”。鉴于此，本文设计一种基于灾变思想的改进遗传算法(Improved Genetic Algorithm with Catastrophe Theory,IGACT)生成列车停站方案，求解步骤如下。

Step 1 初始化

车站有序编号集合Ω={1,…,i,…,j,…,N}；研究时段T内列车有序发车编号集合K={1,2,…,k,…} ；车站之间的出行需求Q={qi,j|i,j∈Ω}；令方案Γ=∅，方案索引m=1，方案数2M；最优个体Γ+=∅；进化迭代索引ω=1，最大迭代次数ωmax；内循环索引ω′=1，最大内循环次数M；触发灾变索引ω″=1，最大触发灾变次数ωmax″。

Step 2 生成初始方案

Step 2.1 如果m ＜2M，在满足特殊车站停站约束条件下，根据是否停站的0-1变量对前Mnum列车进行编码，通过循环组合生成个体Xm，编码过程如图5所示，转Step 2.2；否则，已生成2M个初始方案Γ，找到最优适应度值Z+及相应的个体X+，Z+=f(X+)=min[f(X1),…,f(X2M)]，转Step3。

图5 解的编码Fig.5 A schematic diagram of encoding progress for a solution

Step 2.2 根据首站等间距发车原则，初始化各列车首站发车时间；根据首站发车时间及列车运行时间参数，计算所有列车在各站到站时间及发车时间。

Step 2.3 根据追踪间隔、列车连续跨站数量和车站连续跳停列车数量约束判断解是否可行。如果满足约束，计算目标函数作为适应度值f(Xm)，令Γ(0)=Γ(0)∪{Xm}，m=m+1，转Step 2.1；否则，直接转Step 2.1。

Step 3 遗传算法迭代优化

Step 3.1 如果ω ＜ωmax，转Step 3.2；否则，已完成迭代优化，转Step 5。

Step 3.2 如果ω′＜M，采用轮盘赌方法选择两个个体Xa,Xb，且Xa≠Xb，转Step 3.3；否则，找到第ω代最优适应度值，令ω=ω+1，ω′=1，转Step 4。

Step 3.4 在1～|N·Mnum|范围随机生成p1，如果p1∈Θ({1,N} ∪Ω*)，p1位置无效，重新生成p1，其中，Θ({1,N}∪Ω*)为列车在始发、终到站和关键车站的位置标志；否则，p1位置有效。依次找到后续γ组列车相对应的位置γ|N·Mnum|+p1。对应位置同步采用变异操作生成

Step 4 灾变操作

Step 4.2 如果ω″＜ωmax″，转Step 3.1；否则，令Γ+=Γ+∪{X+}，ω″=1，转Step 2。

Step 5 循环结束

输出最优方案Z*=min(Z+,Γ+)。

4 案例研究

北京地铁15号线全长41.4 km，连接海淀区、朝阳区与顺义区，客流呈现明显的长距离出行特征，以2023年3月6日客流数据为例，当日客流平均运距14.88 km，平均乘车站数7 站，平均乘车时间达22.16 min。此外，客流潮汐特征显著，2023年3月6日7:30-8:00时段的断面客流数据如图6所示。

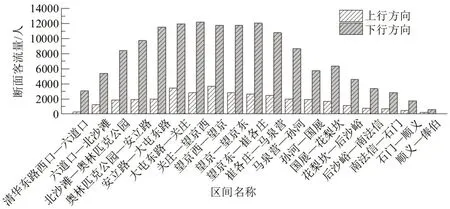
图6 7:30-8:00时间段的区间断面客流量Fig.6 Section passenger flow volume during 7:30-8:00 time period

15 号线设有车站20 座，其中，换乘站5 座，7:30-8:00 时段各车站的上下车客流数据如图7所示。

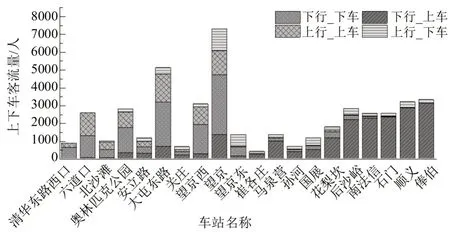
图7 7:30-8:00时间段车站上下车客流量Fig.7 Passenger flow boarding and alighting during 7:30-8:00 time period

由图7可知：①列车在换乘站望京、大屯路东、望京西、奥林匹克公园和六道口的客流量均很大，换乘站应作为必须停车的关键车站；②下行方向，列车从俸伯到后沙峪几个车站的上车客流量均较大，上述车站可考虑作为关键车站。

为缓解早高峰不均衡的客流压力，北京地铁在客流量较小的上行方向开行两种停站方式的大站快车，即连续跳停南法信、石门及顺义这3站，以及连续跳停崔各庄、马泉营、孙河、国展及花梨坎这5站。但是，该跳停方案连续跳停车站数量较多，且未考虑客流量较大的下行方向。在实际运输组织作业过程中，如果连续跳停车站数量太多，不但会增加跳停站乘客的等待时间，而且不便于跳停区间乘客的出行。此外，不宜采用过于复杂的停站组合方式，否则，不仅会影响乘客的乘车体验，也给车站工作带来巨大的压力。鉴于此，本文以乘客总出行成本最小为优化目标，采用IGACT 算法生成列车停站方案。案例中相关参数取值为：ωmax=500，ωmax″=20，M=100，Mt,max=5，Ms,max=2，Mnum=3，Maccess=1。

以早高峰下行方向为例，令Ω*={清华东路西口，六道口，奥林匹克公园，大屯路东，望京西，望京，俸伯}，IGACT算法迭代收敛情况如图8所示。

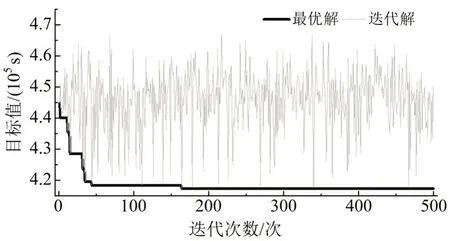
图8 IGACT算法迭代收敛示意图Fig.8 Schematic diagram of iterative convergence in IGACT algorithm

由图8可知：①迭代到第163代，最优目标值不再随迭代次数的增加而降低，因此，可认为算法已收敛；②经过500次迭代，最优解为417421.14 s。

采用传统GA 算法进行4 次实验，实验结果如图9所示。

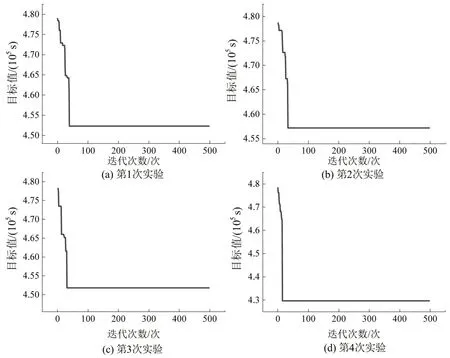
图9 传统GA算法迭代收敛示意图Fig.9 Schematic diagram of iterative convergence in traditional GA algorithm

由图9可知：传统GA 极易陷入局部最优，在图9(a)～(d)的4 次实验中，每次结果都不一样，且均未找到最优解。相较于传统方法，本文提出的IGACT 算法因为结合了灾变思想，在迭代寻优过程中可以跳出局部最优，进而找到最优解。

设计3种基于不同关键车站的场景：场景1，采用当前实际应用的停站方式；场景2，上行方向仅选取始发终到站作为必须停车的关键车站，下行方向选取换乘站和始发终到站；场景3，上行方向选取换乘站和始发终到站，下行方向选取换乘站、始发终到站以及从俸伯到后沙峪各站。采用IGACT算法分别基于上行和下行方向客流量以及关键车站计算不同场景条件下的最优停站方案，结果如表2所示。需要说明的是，根据客流量计算该时段需开行9 列列车，考虑停站方式为3 种，即开行3 组相同停站方式的列车，表2中仅绘制其中一组。

表2 不同场景条件下的停站方案的优化结果对比Table 2 Comparison of optimized results for stopping schemes under different scenario conditions

由表2 可知：①列车在设定的关键车站均停车，场景1跳停(3+5)×3=24站，场景2跳停45站，场景3 跳停33 站；②场景2 和场景3 中的跳停策略更加灵活，跳停车站非全部连续，其中，下行方向该时段几乎都是上车乘客，由于列车载客量高于设定的满载率阈值，因此，下行方向部分列车在某些车站采用了跳停方式；③场景1 的目标值最差，乘客总出行成本高达608987.17 s，场景2 的目标值最优，为534692.91 s；④相较于场景1，场景2目标值提升了12.20%，场景3提升了4.28%。

不同场景条件下的列车运行情况如图10 所示，由图10可知：

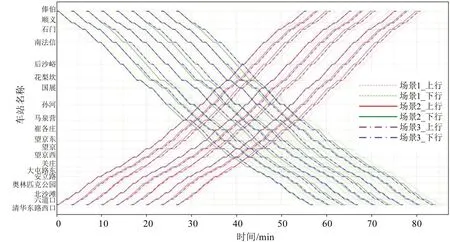
图10 3种场景条件下的列车运行图Fig.10 Train diagram under three different scenario conditions

(1)在3种场景中，列车均满足特殊车站停站和安全追踪间隔等约束条件。

(2)对应发车次序的列车在始发站的发车时间均相同，因此，跳停车站数量越多，列车到达终点站的时间越早。对于下行方向，由于场景2 和场景3跳停部分车站，而场景1采用站站停的方式，因此，场景2和场景3中列车到达终点站的时间均早于场景1，场景2早到17.49 s，场景3早到17.97 s。

(3)以该时段相邻列车在车站发车间隔Di,k的偏差均值Mdev和偏差离差Sdev作为评价运行图均衡性的指标，Mdev和Sdev值越大，代表偏离程度越大，即运行图发车间隔越不均衡；反之，当Mdev=Sdev=0 时，代表完全等间隔发车。

运行图发车间隔均衡性计算结果如表3所示。

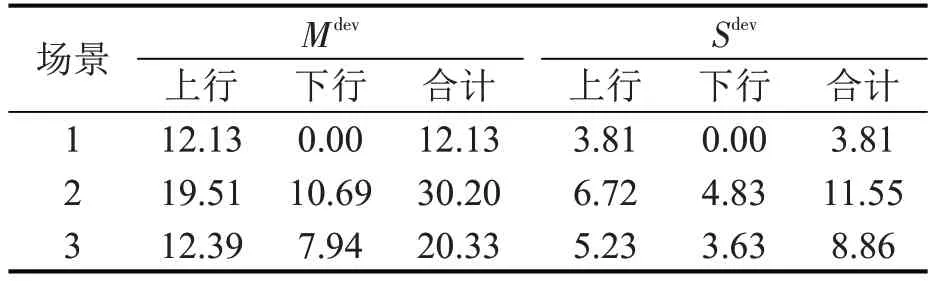
表3 运行图发车间隔均衡性计算结果Table 3 Calculation results of departure-interval equilibrium of train diagram

由表3 可知：场景1 的Mdev(12.13)和Sdev(3.81)均是最优的，场景3的发车间隔均衡性(20.33，8.86)优于场景2(30.20，11.55)。

3种场景条件下列车离开车站时的载客量情况如图11 所示，其中，场景1 上行列车编号1～9，下行列车编号10～18，后续列车编号依此类推。

图11 列车离开各车站时载客量的热力图Fig.11 Heatmap of passenger load as trains depart from stations

由图11可知：①总体上，列车在下行方向离站时的载客量大于上行方向，在中间车站的载客量大于两端车站；②列车运行图发车间隔均衡性越好，相邻列车离站时的载客量差异也越小，场景3 中，列车离站时的载客量差异优于场景2。

综合分析3种场景可知：①采用本文提出的考虑列车容量约束的停站方案优化方法，可节约长距离客流出行时间，降低乘客总出行成本，同时，更好地匹配列车满载率与上车客流需求；②约束必须停车的车站数量越少，算法可得到方案的乘客总出行成本更优，但是，过于灵活的停站方案可能导致相邻列车的发车间隔均衡性变差，使离站时相邻列车的载客量差异变大。

5 结论

针对具有长距离出行和时空分布不均衡客流特征的郊区线路，在高峰时段列车实际载客量受列车容量约束存在乘客滞留站台的现象，本文考虑留乘乘客、进站或者换乘乘客的候车时间以及乘客的旅行时间，建立以乘客总出行成本最小为目标的优化模型，并基于灾变思想设计一种IGACT 求解算法，实现考虑列车容量约束的停站方案优化。此外，定义了运行图发车间隔均衡性评价指标，以更好地服务出行乘客。以北京地铁15 号线的实际运营数据进行了案例验证。本文得到的主要结论如下：

(1) 相较于传统GA 算法，设计的IGACT 算法通过灾变操作可有效跳出局部最优。实例中，第163 代时，最优目标值不再随迭代次数的增加而降低，算法已收敛。

(2)设计3种以始发终到站、换乘站或者大客流站作为关键车站的场景，采用IGACT 算法可得到不同场景条件下的最优停站方案。实例中，场景1乘客总出行成本为608987.17 s，场景2 为534692.91 s，场景3 为582919.51 s，相较于场景1，场景2和场景3目标值分别提升12.20%和4.28%。

(3)采用跳停策略，可以有效减少列车运行时间，加快车底周转，提升高峰时期运力。实例中，相较于场景1，场景2和场景3的下行方向到达终点站时分别节省17.49 s和17.97 s。

(4)相邻列车的停站方式将影响列车运行图发车间隔均衡性，而运行图发车间隔均衡性与列车离站时的载客量差异呈正相关关系。实例中，场景3生成运行图的发车间隔均衡性优于场景2，列车离站时的载客量差异也更小。因此，虽然场景2目标最优，但是，综合考虑运行图发车间隔均衡性，本文更加推荐场景3的停站方案。

本文研究的多样化停站方案对出行乘客提出了更高的要求，一定程度上增加了乘客乘车选择以及车站运输组织的难度。基于高峰时段主要客流为常旅客的有利条件，运营企业可以通过提前公布列车时刻表，在站内和车内分别采取多种配套服务措施引导乘客乘车，乘客也可以根据实际到站时间，结合列车时刻表和出行过程中的信息提示选择合适的乘车方案。