涵盖全面 重视基础 兼顾发展——2023年安徽中考第22题印象

安徽省合肥市第四十八中学 (邮编:230002)

安徽省蚌埠市教育科学研究所 陈耀忠 (邮编:233000)

2023年安徽省初中学业水平考试顺利进行,数学试卷中第22题成为广大一线教师的关注热点. 对比近三年的安徽中考压轴题,感觉命题技术特别娴熟,2021年的位似变换、2022年对称构图、2023年旋转入题,应该是一种有意而为之的设置.本文针对2023年安徽中考第22题,从解题研究、试题研究、变化研究等视角展开讨论,限于个人水平,请同行批评指正.

1 试题及解

试题(2023年安徽中考第22题)在Rt△ABC中,M是斜边AB的中点,将线段MA绕点M旋转至MD位置,点D在直线AB外,连接AD,BD.

(1)如图1,求∠ADB的大小;

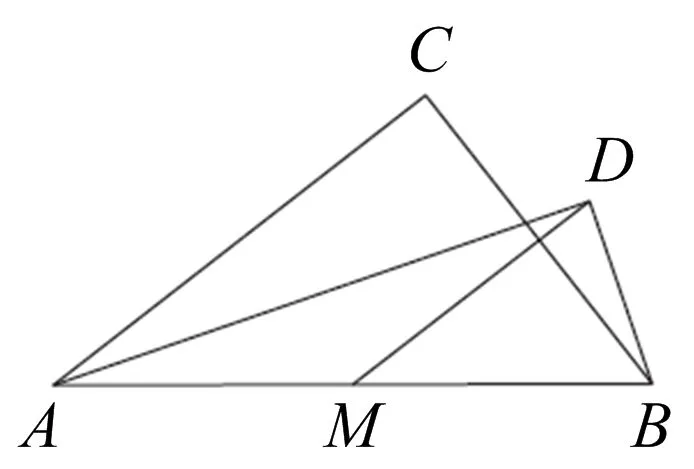
图1

(2)已知点D和边AC上的点E满足ME⊥AD,DE∥AB.

(ⅰ)如图2,连接CD,求证:BD=CD;

图2

(ⅱ)如图3,连接BE,若AC=8,BC=6,求tan∠ABE的值.

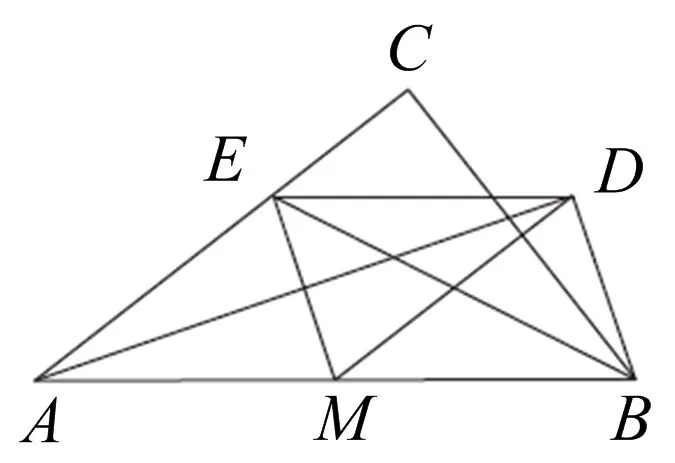
图3

解答(1)(方法一)由题意,MA=MD=MB,所以∠MAD=∠MDA,∠MBD=∠MDB, 而∠MAD+∠MDA+∠MBD+∠MDB=180°,故∠ADB=∠MDA+∠MDB=90°.

(方法二)如图4,倍长DM至N,则AB,DN相互平分,证明四边形ADBN是矩形.

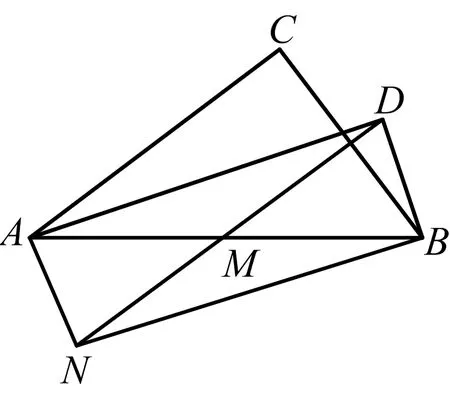
图4

(方法三)如图5证明点D在以AB为直径的圆M上.

图5

(2)(ⅰ)先证明四边形MAED是平行四边形.

(方法一)从而MD∥AC,故MD⊥BC,即∠CFD=90°=∠BFD,

又M是中点,所以DM与BC的交点F(如图6)是BC的中点,即CF=BF,而DF是公共边,故△CDF≌△BDF,于是BD=CD.

图6

(方法二)同方法一,先证CF=BF,再证MD是线段BC的垂直平分线,于是BD=CD.

(方法三) 如图7,连接MC,证△MBC是等腰三角形,故∠CMD=∠BMD,从而△CMD≌△BMD,BD=CD.

图7

(方法四)先证CF=BF,如图8,作EN⊥AB于点N,先证△EMN≌△BDF,再证Rt△ENM≌Rt△CDF,从而CD=EM=BD.

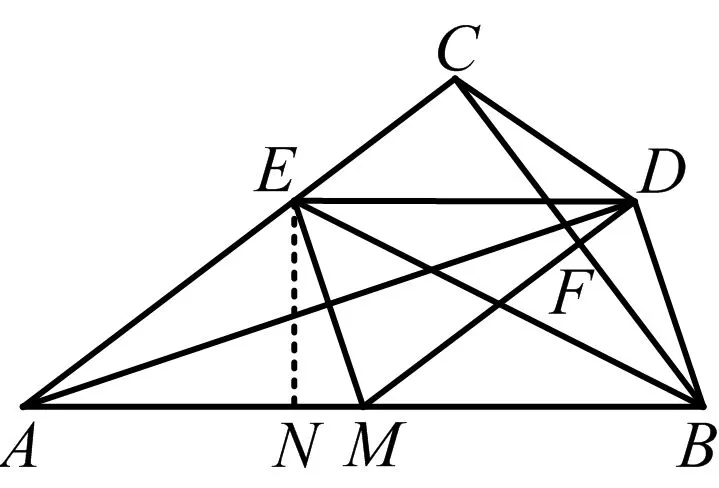
图8

(方法五)如图9,证Rt△MEH≌Rt△BDF,得EH=DF,再证Rt△MEH≌Rt△CDF,从而CD=EM=BD.

图9

(方法六)如图9,证△AEM≌△MDB,得BF=MH=CF,再证

Rt△MEH≌Rt△CDF,从而CD=EM=BD.

(方法七)如图10,连接MC,则△MBC是等腰三角形,再证∠CMD=∠BMD,根据圆的定义知,B,C,D三点在以AB为直径的⊙M上,所以BD=CD.

图10

(方法八)如图11,作EH⊥MD于点H,△BMD≌△EDM⟹BF=EH=CF⟹△BDF≌△CDF,从而BD=CD.

图11

(方法九)如图11,作EH⊥MD于点H,△BFD≌△EHM⟹BF=EH=CF⟹△BDF≌△CDF,从而BD=CD.

(方法十)如图12,连接MC,作MF∥CD,交AC于点F.则AE=DM=CF,从而AF=CE,而AM=CM,∠FAM=∠ECM,所以△FAM≌△ECM,故CD=FM=EM=BD.

图12

(方法十一)如图7先证MAED是菱形,故AE=AM=MC=MD,因而△AEM≌△MCD⟹CD=EM=BD.

(方法十二)MAED是菱形,所以,∠MAD=∠EAD,根据圆的定义,易证A,B,C,D都在以AB为直径,M为圆心的圆上(如图13),由圆周角相等得BD=CD.

图13

(方法十三)如图13,根据圆的定义知,B,C,D三点在以AB为直径的⊙M上,根据垂径定理,BD=CD.

(方法十四)MAED是菱形,∠MAD=∠EAD,如图14,由(1)AD⊥BD,所以△ABF为等腰三角形,从而BD=DF,根据圆的定义,易证A,B,C,D都在以AB为直径,M为圆心的圆上,∠F=∠ABF=∠FCD,故DF=CD,从而BD=CD.

图14

(方法十六)MAED是菱形,所以∠DCB=∠DAM=∠DAC=90°-∠AEM=∠EMH(如图15,MH⊥AC),而MD∥AC,故MH=CF,所以Rt△MEH≌Rt△CDF,于是CD=ME=BD.

图15

(方法十七)所以MD∥AC,而AC⊥BC,且M是AB中点,记BC,MD的交点为F,则F为BC的中点,且MD⊥BC.

如图16,截取FG=FD,则DG,BC垂直平分,所以四边形BDCG是菱形,从而BC=CD.

图16

(ⅱ)由题意,AB=10,从而MA=MB=5.

(方法一)如图17,作EH⊥AB于点H,记BC,AD相交于点F.

图17

由(ⅰ),MAED是菱形,所以AE=AM=5,CE=3.因为S菱形AMDE=AM·EH=AE·CF,所以EH=CF=BF=3.

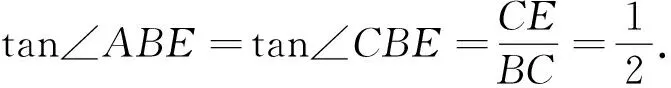
(方法二)如图17,作EH⊥AB于点H.由(ⅰ),BF=FC=3,AE=AM=5,从CE=3.又因为四边形BDEM是平行四边形,

所以EM=BD,∠EMH=∠DBA=∠BDF,∠EHM=90°=∠BFD,

所以△EMH≌△BDF,从而EH=BF=3=CE, 故BE平分∠ABC,

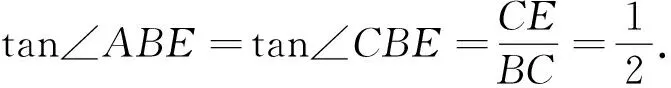
(方法三)如图17,作EH⊥AB于点H. 由(ⅰ),MAED是菱形,所以AE=AM=5,

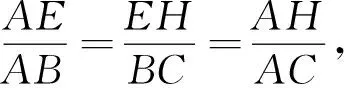
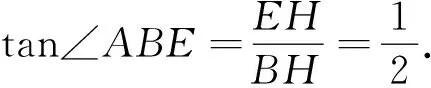
从以上解答可以看出,本题难度不大,通过线段旋转产生的图形,从一般性质出发,通过逐步增加条件,使得图形的性质越来越丰富、特殊,解题过程中出现了三角形内角和定理的运用、等腰三角形的性质、直角三角形的性质,矩形的判定与性质、圆的概念及性质、平行四边形的判定与性质、菱形的判定与性质,旋转的性质、对称的应用,应该说考查内容极其丰富. 本题三小问起点较低、入口极宽,中间的问题承上启下,成为解题的核心,最后一问蜻蜓点水,给研究者留下极大空间.

2 试题研究

2.1 图1的一个结论

命题1如图,已知∠ACB=∠ADB=90°,AC=BC.

图18

图19

(2)如图19,作CE⊥AD于点E,CF⊥DB于点F,类似即证!

2.2 图2的出处及价值

本题图2出处与阿拉伯著名数学家、天文学家阿尔·卡西有关,阿尔·卡西在其著作《圆周论》中叙述了圆周率π的计算方法,与阿基米德、刘徽一样,也采用求圆内接和外切正多边形周长的方法[1],但计算过程完全不同,为方便说明,以现代的方法解释他给出的公式:

如图20,阿尔·卡西在分割过程的计算中,利用了下面的递推公式:

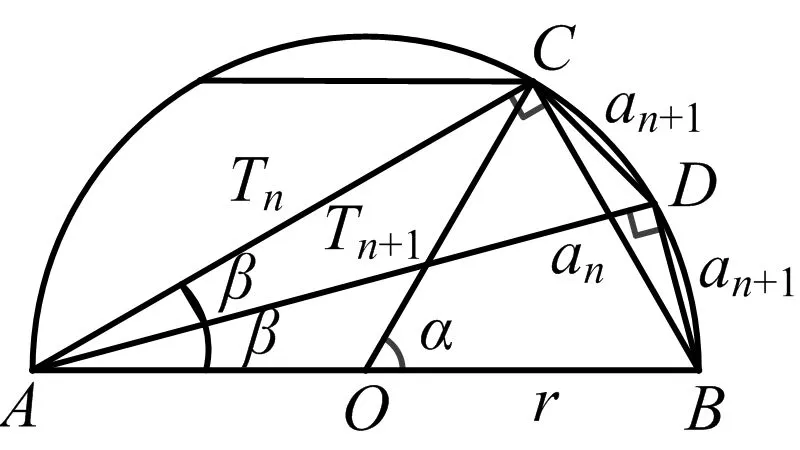
图20

当时,采用的60进制,计算了圆内接正3×228的周长,同理计算出圆外切正3×228的周长,得到的近似值为π=3.14159265358979325,有17位有效数字.

2.3 图3教材索源及性质研究

如图21,若记AD,BE的交点为I,则I为△ABC的内心;若补齐△ABF,则AD,BC的交点H是△ABF的垂心.因此,从这些角度来看,本题是三角形内心、垂心的联袂演出.

图21

正因为如此,试题图3有着非常多的性质:

命题2如图22,将⊙M补齐,延长BE交⊙M于点G,记BG,AD交点为I,BC,MD交于点F,AD,EF交于点H,则有

图22

(1)△AEM≌△DEM≌△MBD;

(2)AD,BG分别平分∠CAB,∠CBA,交点I为△ABC的内心;

(3)△IGA∽△IDB∽△ECF,且均为等腰直角三角形;

本题图形给出一种证明下面大家熟知的定理的一种构图思路:

证明如图23,构造Rt△ABC,其中AC=3,BC=4,AB=5,延长CB,CA,分别至点D,E,使得AE=BD=5,则

图23

3 变化研究

3.1 一道流传广泛的试题

命题4已知,AB是半圆的直径,C是半圆周上一点,AD平分∠CAB,交半圆O于点D,在下列条件下分别求AD的长.

(1)如图24,AC=4,BC=3;

图24

(2)如图25,AC=3,BC=4.

图25

3.2 改BC为正六边形一边

阿尔·卡西在圆周率求解中,构图的原始状态就是以正六边形为起点,在这种状态下我们有:

命题5如图26,C,D在半圆M上,AB是半圆直径,∠CAB=30°,点M是AB的中点,MD=MA,ME⊥AC,交边AC于点E,四边形BDEM是平行四边形,则图中所有自然角的度数均是15的倍数.

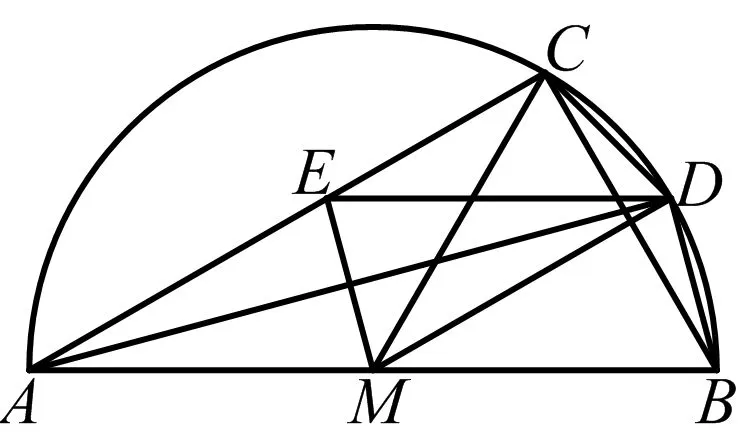
图26

与原题结合,改变点D的位置,有

命题6如图27,C,D在半圆M上,AB是半圆直径,∠CAB=30°,点M是AB的中点,MD=MA,ME⊥AD,交边AC于点E,若DM⊥AB,则

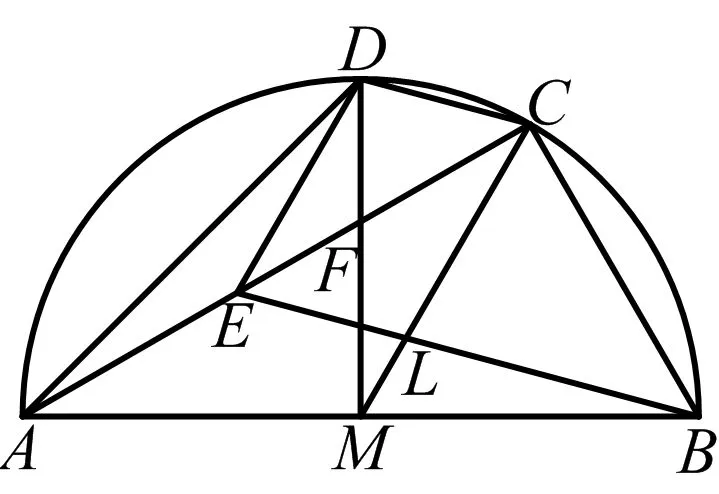
图27

(1)△AEM≌△DEM≌△EDC≌△CLE,且三角形三内角分别为30°,45°,105°;

(2)△MCD∽△DEF∽△EML∽△MLF,且三角形均为顶角是30°的等腰三角形;

(3)△ADM≌△BEC,且均为等腰直角三角形;

(4)四边形CDEM是等腰梯形,其中DE∥CM;

(5)四边形CDEL是平行四边形.

4 后记

就本题而言,从命题角度来看,利用旋转,结合圆的定义自然有A,B,C,D四点共圆;从解题过程来看,本题解法多样,内涵丰富,几乎涵盖了初中平面几何的全部知识,而且难度适中,兼顾基础与发展;通过图形的变化来看,本题图形多变,支撑逻辑众多,对学习平面几何、落实几何素养有着非常好的价值.