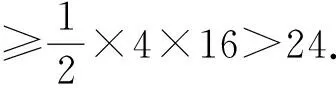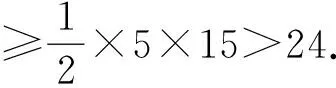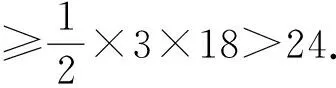周长最短与面积最小的Evans三角形

吴 波 (邮编:401249)

Guy在文献[1]中引述了Evans于1977年提出的如下问题:

问题(Evans问题)[1]求出底能整除(这条底边上的)高的一切整边三角形．

将满足“底能整除(这条底边上的)高”的整边三角形叫作Evans三角形．而此时的底边叫做Evans边,高与此底边之比叫做Evans比．如果一个Evans三角形的三边长是互素的,就叫作本原Evans三角形．

Evans问题虽然尚未完全解决,但国内研究者已经取得到了不少成果,相关文献可以参阅文献[2-5]．

本文拟确定出周长最短与面积最小的Evans三角形,要用到如下结论:

结论1[1]Evans比不可能是1和2,但可以是3．

结论2[6]整边直角三角形一定不是Evans三角形．

结论3[6]有两边相等的整边三角形一定不是Evans三角形．

结论4[2]Evans三角形必定是Heron三角形．

结论5[7]本原海伦三角形的最小边长是3,即不存在边长是1或2的本原海伦三角形．

还要证明如下:

引理1若Heron三角形ABC的高CD为整数,则△ACD,△BCD都是勾股三角形．

注勾股三角形即是整边直角三角形．

证明(1)若Heron三角形ABC中a=b,由文献[8]中等腰的本原海伦数组公式可知:此时△ACD,△BCD是两个全等的勾股三角形．此时结论显然成立．

(2)若Heron三角形ABC任两边不等,如图1或图2．

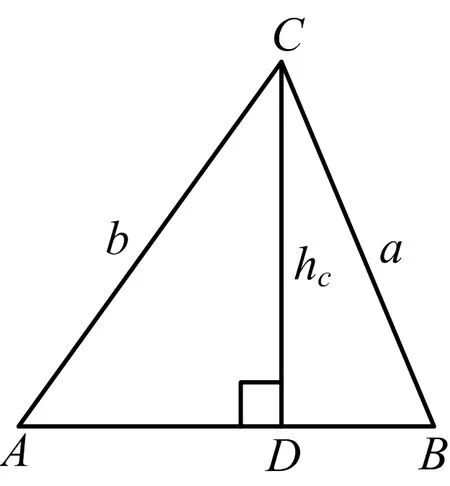
图1

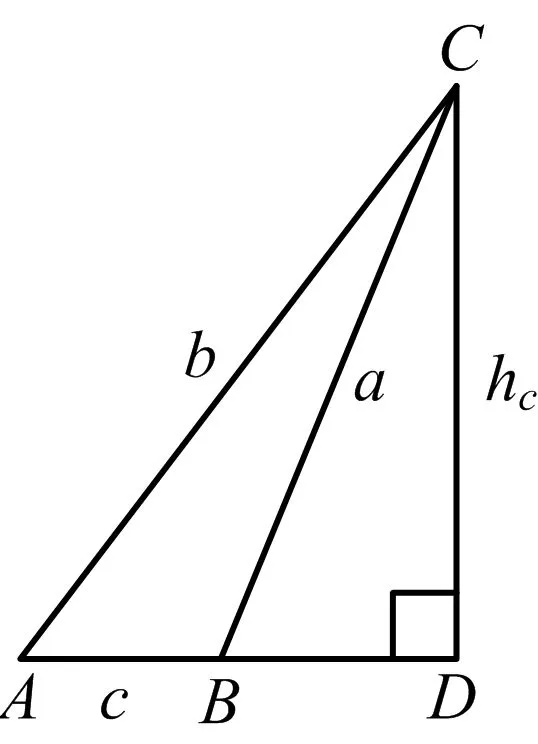
图2

因Heron三角形三边均为整数,由余弦定理可知:cosA,cosB必为有理数．结合图1和图2,由|AD|=b|cosA|,|BD|=a|cosB|知:|AD|,|BD|必为有理数．

而题设中高CD也为整数,由勾股定理并结合“|AD|,|BD|为有理数”可知:|AD|,|BD|必为整数．因此△ACD,△BCD都是勾股三角形．证毕．

引理2若周长最短(面积最小)的Evans三角形ABC的Evans边为c,则A,B中必有一个是钝角．

证明对以c为Evans边的周长最短(面积最小)的Evans三角形ABC,假设A,B都不是钝角,又由结论2知:A,B不可能是直角,则A,B都是锐角,这表明:如图1所示,c边上的高hc必在△ABC内．

Evans三角形为整边三角形,结合Evans三角形定义可知:Evans边c上的高hc必为整数．又由结论4知:Evans三角形必定是Heron三角形．再结合引理1可知:△ACD,△BCD都是勾股三角形．

勾股三角形显然是Heron三角形．这样,由结论5知:|AD|,|BD|中有一个至少为3,另一个至少为4(注意结论3表明:|AD|≠|BD|)．因此c=|AD|+|BD|≥7．

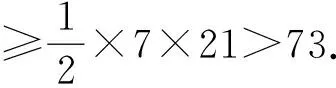
此时△ABC的周长>21+21+7=49．

但我们知道:存在周长小于49且面积小于73的Evans三角形．具体地说,在△ABC中a=13,b=15,c=4．易算得c边上的高hc=12．可以验证它是一个以c为Evans边的Evans三角形．其周长为32<49,面积为24<73．

此Evans三角形的存在与引理2题设中的“最小”相矛盾．矛盾表明:假设不成立．所以A,B中必有一个是钝角．证毕．

定理1周长最短与面积最小的Evans三角形都唯一存在,其Evans边的长为4,另两边长分别为15,13．其周长为32,面积为24．

证明设周长最短与面积最小的Evans三角形ABC的Evans边为c,c边上的高CD记作hc．由引理2可知:a,b在高CD的同侧．如图2,不妨设a

由结论5知:Evans边c最小为3．下面我们分类讨论．

(1)若c=4,而结论1表明:Evans比最小为3．

若Evans比为3．则hc=3c=12．如图2有:

由结论4和引理1知:△ACD,△BCD都是勾股三角形．因此a,b,|AD|,|BD|都是正整数．用因式分解法很容易知道上述方程组有且仅有一组正整数解:a=13,|BD|=5,b=15,|AD|=9,c=4．

这个Evans三角形ABC的周长为32,面积为24．

由勾股定理可知:a>hc=16,b>hc=16．

此时△ABC的周长>16+16+4>32．

此时其周长及面积均大于前述那个Evans三角形．

这表明:此种情形下,其周长不是最短的,面积也不是最小的．

由勾股定理可知:a>hc=15,b>hc=15．

此时△ABC的周长>15+15+5>32．

显然周长及面积均大于前述那个Evans三角形．

这表明:在此种情形下,其周长不是最短的,面积也不是最小的．

(3)若c=3,而结论1表明:Evans比最小为3．

若Evans比为3．则hc=3c=9．如图2有:

|AD|-|BD|=c=3．

用因式分解法很容易知道上面第一个方程组有且仅有一个正整数解:a=15,|BD|=12,b=41,|AD|=40．但它们并不满足第二个方程:|AD|-|BD|=c=3．

这表明:c=3,hc=9且a,b在高CD的同侧的Evans三角形并不存在．

若Evans比为4．则hc=4c=12．如图2,由勾股定理有:

|AD|-|BD|=c=4．

同理可证:此方程组无正整数解．

这表明:c=3,hc=12且a,b在高CD的同侧的Evans三角形并不存在．

若Evans比为5．则hc=5c=15．如图2,由勾股定理有:

|AD|-|BD|=c=5．

同理可证:此方程组无正整数解．

这表明:c=3,hc=15且a,b在高CD的同侧的Evans三角形并不存在．

由勾股定理可知:a>hc=18,b>hc=18．

此时△ABC的周长>18+18+3>32．

显然周长及面积均大于前述那个Evans三角形．

这表明:此种情形下,其周长不是最短的,面积也不是最小的．

综上可知:三边长分别为15,13,4的三角形就是周长最短的Evans三角形,同时它也是面积最小的Evans三角形．证毕．

引理2中证明了周长最短(面积最小)的Evans三角形必定是钝角三角形．其实,文献[6]中有一个一般性的

猜想[6]Evans三角形必定是钝角三角形．

需要说明的是:文献[9]曾经对上述猜想给出过一个“证明”,但这个“证明”并不正确．因为文献[9]中的证明依赖于文献[10]中的“充要条件”,而我们已经发现并给出了具体的反例说明:文献[10]中的“充要条件”是错误的．在文献[10]中的“充要条件”的基础上进行推导的文献[9]和文献[11]中的结论大多并不成立．相关结果将另外撰文予以说明．

因此,对上述猜想有兴趣的读者可以继续探讨．