智慧学习环境下初中数学原理课教学实践与思考——以沪科版数学“勾股定理”为例

安徽省合肥市第四十五中学芙蓉分校 钱 勇 (邮编:230601)

安徽省肥西县严店初级中学 侯守定 (邮编:231232)

安徽省阜南县第二初级中学 孙晓莉 (邮编:236300)

安徽师范大学附属肥西外国语学校 卫德彬 (邮编:231200)

1 问题提出

《义务教育数学课程标准(2022年版)》指出:合理利用现代信息技术,提供丰富的学习资源,设计生动的教学活动,促进数学教学方式方法的变革[1].如何实现现代教育信息技术和数学教学深度融合,为学生提供个性化、协作性的智慧学习环境,提高学习效率,减轻学业负担,发展学生数学素养,是目前一线教育工作者亟需研究的问题.本文首先对学习环境、智慧学习环境、数学原理课进行界定,然后以沪科版数学八年级下册第18章《勾股定理》章首课教学为例,对智慧学习环境下初中数学原理课教学进行探索.

2 概念界定

2.1 学习环境

学习环境是学习活动不可或缺的重要部分,建构主义认为理想的学习环境应由情境、合作、交流和建构四个方面构成.现在以“互联网+”信息技术为基础,有利于创设包含这四种要素的理想的学习环境.

2.2 智慧学习环境

智慧学习环境是一种能识别学习者特征,提供便利的交流工具,学习者根据学习需求,自主获取信息资源,进行信息加工,开展合作探究、互动交流、发现型学习的场所或活动空间[2].

2.3 初中数学原理课

所谓初中数学原理课,是指在初中阶段,教师对学生进行数学公理和定理,包括公式、法则和性质的教学,使学生准确掌握数学原理的条件和结论,掌握其变形的各种形式的一类课型,它能使学生进一步了解知识之间的内在联系,掌握数学知识之间所存在某些定律或联系法则,有助于学生数学思维的发展和问题解决能力的提高．

3 教学实践

3.1 教材分析

勾股定理是平面几何中一个重要定理,它反映了直角三角形三边的关系,本章之前学生已学习了直角三角形的概念和部分性质.在此基础上,本章主要学习勾股定理、勾股定理逆定理及其应用.结合新课程标准,本节课的教学目标为:

(1)经历对问题情境的“观察—猜想—验证”过程,体验勾股定理的发现过程;

(2)了解勾股定理的证明,渗透数形结合思想,培养学生推理能力;

(3)介绍勾股定理发展简史,增强文化自信,激发学生爱国情怀.

3.2 学情分析

学生已经学习了三角形的概念和性质、等腰三角形的性质和判定,初步具备了研究特殊三角形的基本方法,但八年级学生仍以形象思维为主,缺乏推理意识,对几何证明有一定的畏惧之心.为此,在教材处理时调整了探究思路,让教学过程具有渐进性和知识结构具有完整性,使得教与学达到和谐统一.

因此,本课的教学重难点为:

(1)教学重点:理解勾股定理,勾股定理的面积证法;

(2)教学难点:勾股定理发现过程中蕴含的数学思想.

3.3 教学过程

(1)梳理知识,明确结构

①三角形的的研究路径:

②研究方法:观察、猜想、操作、说理验证.

教学意图通过回顾三角形的研究内容和方法,构建研究直角三角形的内容和方法,从整体上了解本章知识结构.

(2)创设情境,引发猜想

情境1毕达哥拉斯是古希腊著名的数学家和哲学家.相传毕达哥拉斯应邀参加一次宴会时,被脚下排列规则、美丽的方形石砖所深深吸引,如图1,他惊奇地发现以对角线AB为边长的正方形面积恰好等于两块砖的面积和.

图1

情境2中国古代称短的直角边为勾,长的直角边为股,斜边为弦.公元前十一世纪,数学家商高就提出“勾三、股四、弦五”.如图2,直角边长分别是3和4,你能验证这个结论吗?

图2

图3 图4

猜想直角三角形两直角边的平方和,等于斜边的平方.

教学意图通过数学家发现勾股定理的趣事轶闻创设情境,激发学习兴趣,积极探索,引发猜想,让学生学会用数学的眼光去观察世界.

(3)验证猜想,得到定理

思考对于一般的直角三角形,刚才的结论还成立吗?如何确定它的正确性呢?

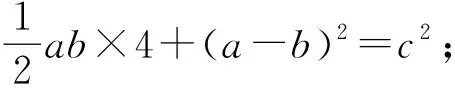
图5 图6

让学生通过智慧课堂中“数学画板”,探索勾股定理的不同证明方法.

教学意图引导学生通过类比得到证明方法,经历定理的探究过程,积累数学活动基本经验,体会问题解决策略的多样性,渗透由特殊到一般的数学思想方法,培养学生的数学发散思维,发展学生几何直观素养和逻辑推理能力.

(4)介绍历史,渗透情怀

公元三世纪,汉代数学家赵爽对《周髀算经》内的勾股定理作出了详细注释,记录于《九章算术》中“勾股各自乘,并之为弦实,开方除之即弦”,赵爽创制了一幅“勾股圆方图”,用数形结合得到方法,给出了勾股定理的详细证明.

播放视频资源数学史话——勾股定理.

教学意图通过历史介绍,渗透数学文化,激发学生学习兴趣和自信心,增强民族自豪感,厚植爱国情怀.

(5)定理应用,内化理解

①在△ABC中,∠C=90°,AB=c,BC=a,AC=b.

(ⅰ)a=6,b=8,求c;(ⅱ)a=8,c=17,求b.

②在三角形中,已知两边长分别是3和4,求第三边的长.

教学意图学生独立完成后,拍照上传智慧学习平台,教师及时了解学生掌握情况,检测教学目标达成度.

(6)课堂小结,形成结构

①回顾本节课的学习历程,说说勾股定理的内容及注意事项.

②总结本节课学习涉及的思想方法:割补法、特殊与一般、数形结合等.

③三角形知识结构:

教学意图引导学生回顾学习历程,让学生归纳三角形知识结构,感悟数学思想方法,初步形成研究“图形与几何”的基本途径.

(7)作业布置,提升能力

必做题:

①习题19.1第1、2题.

②查阅资料:通过网络搜集勾股定理发展简史以及相关故事趣闻,并在学习平台上分享成果.

选做题:勾股定理的证明方法很多,《毕达哥拉斯命题》一书中收集了300多种证法,传统证法使用“面积法”,课后查阅网络资源了解勾股定理其它的证明方法.

教学意图分层作业,注重个人差异,巩固所学知识,学会与他人交流,分享学习成果.

3.4 课后反思评价

(1)探究活动环节,你在小组中做了什么?

(2)列出自己感到困惑的问题.

(3)是否可以总结学习“几何与图形”的一般思路?

教学意图自我评价与教师评价、过程性评价与终结性评价相结合,创新教学评价方式,学生全程参与评价过程,培养学生批判性思维,促进学生反思性学习.

4 教学思考

4.1 融入数学文化教育,厚植学生文化自信

智慧学校环境中的数学文化素材较为丰富,在日常教学中,教师要根据教学内容,挖掘教材,融入数学文化教育,让学生了解一点数学史、数学家的故事,激励学生努力学习,探索未知世界的奥秘.例如,在“勾股定理”教学中,智慧学校环境优选勾股定理的资源,同时作为热门消息第一时间推送到学生端,让教师循数学家的足迹探索勾股定理,激发学生探究热情;学生亦可通过智慧学校的网络资源,了解勾股定理的前世今生,了解勾股定理对数学发展的重大意义,了解我国古代数学家的贡献,从而提高学生学习数学的兴趣,增强学生文化自信,深植学生的爱国素养.

4.2 探寻原理发现过程,培养学生探索精神

纵观数学历史的发展不难发现,原理的产生源于扎实的基础知识与善于发现、质疑的精神.然而初中生无法有数学家深厚的基本功与敏锐的观察力,智慧学校环境捕捉到这种现象,因此在本节课的资源库中,会备存优质的云资源,如AR体验勾股定理发生的场景,以第一视角再现定理产生.在云资源中还有短文、微课、视频、动画等形式多样的资源供学生参看,激发学生的探索精神.探寻数学原理发现过程,能够让学生了解所学知识的背景,从而加深学生对知识的理解,认识到数学的发展正是我们生产生活的需要.本课以“勾股定理”发展史为时间轴,通过情境引入,设计定理的发现路径,让学生经历“特例—猜想—验证—应用”的过程,体会从特殊到一般和数形结合解决问题的方法,感悟数学抽象、推理、模型的思想,发展学生数学素养.

4.3 数据驱动智慧评价,促进学生反思学习

智慧学习环境下,评价不应该只局限于线下评价,还要关注学生在线学习的表现.学生在线上学习过程中,会产生大量的实时动态数据,例如在线讨论情况、视频观看时长频率、各教学环节答题情况等.教师根据学习平台的数据,主要从在线作业、在线评测、作品展示、合作交流等方面进行线上评价,激励学生自主学习,关注学生的学习全过程,积累学习行为数据,对学生进行发展性评价,促进学生反思性学习.

5 结束语

综上所述,智慧学习环境下,立体化的交流平台、数字化的学习工具、智能评测系统等有效运用,改进教学方式方法,提升学生的探究热情,激发学生数学学习兴趣.关注学生已有知识结构,根据课程标准要求,精准分析学情,精准确定教学目标,融入数学文化教育,探寻数学原理发现历程,发展学生数学素养.