初中数学结构化教学的实践
南琼
摘 要:在初中数学教学中积极开展结构化教学活动,有助于学生构建系统的知识网络,加深对数学知识的结构化认识,促进深度学习真实发生,发展数学核心素养。文章以“一次函数”为例开展结构化教学实践,认为将教学内容的结构化分析、数学知识的结构化呈现、重要内容的结构化理解、知识体系的结构化梳理、重点知识的结构化拓展融入教学的各环节中,可获得较好的预期教学效果。
关键词:初中数学;结构化教學;单元教学;一次函数
结构化教学是基于教学环境、材料、程序的组织与系统安排展开教学活动的一种授课方法。《义务教育数学课程标准(2022年版)》(以下简称《标准》)在“教学建议”中强调“注重教学内容的结构化”“重视单元整体教学设计”。结合北师大版《义务教育教科书·数学》八年级上册第四章“一次函数”的内容开展结构化教学活动,是践行《标准》内容的具体体现,能够为初中数学教学带来新的思路和有价值的借鉴。
一、课前准备——教学内容的结构化分析
课前准备是“一次函数”单元教学的重要环节之一,关系着结构化教学质量及授课目标能否顺利达成。课前准备需要考虑的内容非常多,其中对教学内容进行结构化分析是重中之重。对教学内容进行结构化分析应着重考虑教学内容和教学流程两个方面,其中对于教学内容,应明确各知识点在整个单元知识体系中的地位及与其他知识之间的逻辑联系,确保在教学实践中分配合理的授课时间和精力。不仅如此,为保证结构化教学过程中各教学内容之间的有效衔接,分析结构化教学内容时应注重整个单元教学流程的呈现,以更好地设计教学课时,并为更好地处理新、旧知识之间的过渡提供良好指引。
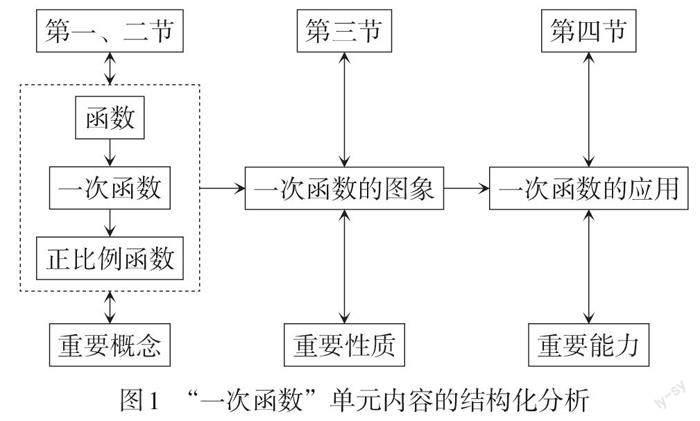
例如,“一次函数”一章包括函数、一次函数与正比例函数、一次函数的图象、一次函数的应用四节内容。从单元整体视角来看,前两节内容主要介绍函数、一次函数、正比例函数三个基本概念,第三节从图象视角对一次函数性质进行讲解,第四节内容讲解一次函数的应用。四节内容层层递进,知识难度逐渐深入。为帮助学生对该章内容有整体的把握和清晰的认识,教师在课前准备时可以使用图1实现对该章内容的结构化分析。
由图1可以清晰看到,教学内容包括三个重要概念、一次函数的图象、一次函数的应用。其中,在概念理解上,要求学生牢记函数、一次函数、正比例函数的概念,把握三个概念之间的关系,认识到一次函数是函数的一种,而正比例函数是一次函数的特例。在一次函数的图象上,要求学生掌握一次函数、正比例函数图象的画法,并能正确描述当k > 0和k < 0时,一次函数、正比例函数中y随x的变化关系,能在同一平面直角坐标系中分析一次函数图象的关系。在一次函数的应用上,要求学生能灵活运用所学知识分析、解决实际问题。整个单元的教学按照“重要概念—重要性质—重要能力”的顺序推进,待学生切实理解、掌握旧知识后,再进行新知识讲解,促使其由基础知识掌握向重要能力稳步进阶。
二、教法运用——数学知识的结构化呈现
在“一次函数”单元教学中,教师应该重视教学方法的总结和对优秀教学方法的借鉴,直观展现学习的重点与难点、知识点之间的逻辑关联,化抽象为具体。笔者发现运用一些教学软件进行授课不仅能增加教学的趣味性,还能为结构化呈现数学知识带来诸多便利。因此,在“一次函数的图象”教学中,教师可以借助如几何画板一类的教学软件,配合多媒体技术的使用,为学生动态展现一次函数图象的绘制过程,并运用文字语言进行描述,通过一次函数图象、文字语言的结构化呈现,帮助学生将图形语言和文字语言对应起来,加深学生对一次函数图象性质的认识与理解。教师还可以运用MindMaster思维导图软件将“一次函数”一章的相关知识点绘制出来,加深学生对本章内容的整体性认识,使学生在头脑中建立结构化、层级化的知识网络,构建完善的知识体系。
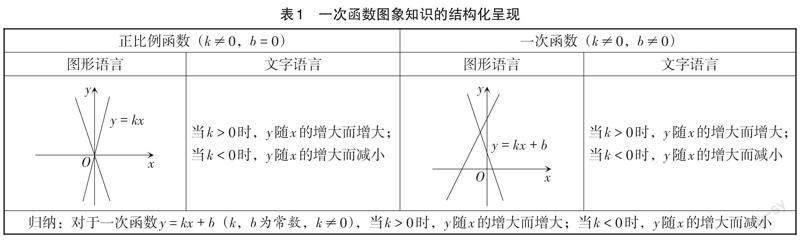
在“一次函数”单元教学中,教师可以将在几何画板软件中采用描点法绘制图象的过程通过多媒体屏幕展现出来,使学生掌握一次函数图象的绘制步骤。为使学生更好地掌握一次函数图象的性质,教师可以在多媒体屏幕上结构化展现该部分内容,如表1所示。
课堂教学时从正比例函数图象的绘制、性质的研究切入,逐渐过渡到一次函数图象的研究中,分别从图形语言、文字语言进行结构化展示,既加深学生的印象,又能使学生亲身参与到数学知识的形成中,深刻体会由特殊到一般的推理过程。
三、授课引导——重要内容的结构化理解
在“一次函数”单元教学中,教师要引导学生做好重要内容的结构化理解,及时走出理解误区,这将对学生数学核心素养的发展大有裨益。重要内容的结构化理解,是指对重要知识点之间的关联、重要知识适宜解决的问题类型、运用重要知识点解决问题的思路等方面的理解。引导学生结构化理解重要内容的方法有多种,其中课堂互动、课堂讨论较为常用。课堂互动能拉近师生之间的距离,激活数学课堂氛围,驱使学生深度思考问题。课堂讨论能凸显学生的学习主体地位,活跃学生分析问题的思维,使之把握分析问题的关键。为保证课堂互动富有成效地开展,教师应深思熟虑,做好互动问题的设计,将重点放在指引学生理解重要内容,以及重要内容之间是如何建立的。另外,为促进单元授课目标的达成,激发学生课堂讨论兴趣,教师应从整个单元视角进行生活化问题的设计,预留空白课堂时间,引导学生主动回顾所学,积极进行课堂讨论,通过对所学内容的整合、重要内容的结构化理解,寻找解决问题正确、有效的切入点。
在“一次函数的应用”教学中,教师结合教学经验,在多媒体屏幕上展示如下问题,给学生预留10分钟的课堂讨论时间,使之主动寻找解决问题的思路。
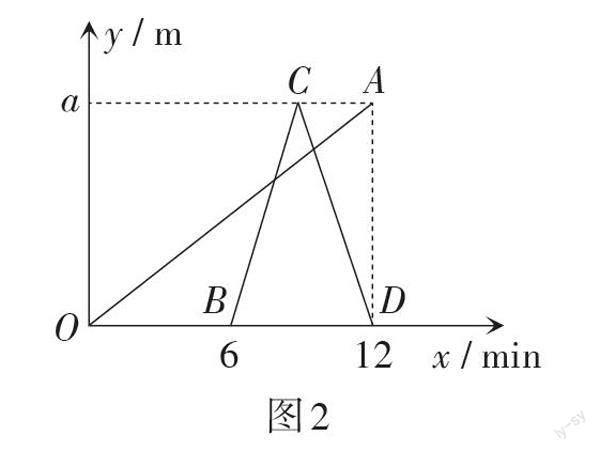
题目 小林以50 m / min的速度步行去离家a m的公园散步,出发6 min后,小林的哥哥骑车沿着同一路线去公园。小林的哥哥到达公园后立即原路返回。两人离家的距离y(单位:m)和小林出发的时间x(单位:min)的函数关系,如图2所示。
(1)a的值为_____;
(2)求CD所在直线的函数表达式;
(3)两人第二次相遇时与公园的距离是多少?
该题主要考查学生对一次函数知识的灵活运用,需要学生在讨论时明确一次函数概念、一次函数图象的性质、一次函数表达式的求法、一次函数与一元一次方程关系等重要内容。课堂上,教师可以指引学生观察图象,思考坐标轴、交点表示的含义,结合对题意的理解和对图象中隐含信息的深入挖掘,建立已知条件与所求问题的联系,探寻正确的解题思路。学生在思考、讨论过程中形成了求解问题的正确思路,积累了一定的实践经验,获得了良好的结构化理解效果。
四、课堂总结——知识体系的结构化梳理
围绕“一次函数”单元开展结构化教学活动时,教师应及时组织学生进行课堂总结,通过对本单元知识体系的结构化梳理,助力结构化教学目标的达成。在“一次函数”单元知识体系的结构化梳理时,教师既要给予学生梳理思路、梳理方向的指引,又要做好梳理过程的跟踪和梳理结果的检查。课堂上,教师可以要求学生确立梳理的关键词,如以“基础知识”为关键词进行“一次函数”重要概念、重要性质、重要能力的梳理,同时以“解题技能”进行常见题型、解题思路、解题思想的梳理。通过“基础知识”和“解题技能”两方面的并行梳理,进一步夯实学生的知识基础,提高学生的基本技能。在梳理过程中,教师应通过观察,与学生交流,把握学生梳理的进度。尤其指引学生使用概念图、思维导图等可视化工具,提高梳理质量,更为清晰地展现知识体系的结构。当然,教师还应做好梳理结果的检查和评价,借助鼓励性语言肯定学生的付出,满足学生的心理预期。
“一次函数”单元教学任务完成后,教师可以围绕单元内容制作多媒体课件,引导学生快速回顾本章内容。同时,讲解概念图和思维导图的绘制方法,要求学生结合所学知识的先后顺序,对所学知识的理解,从“基础知识”“解题技能”两个视角出发,借助绘制的图示完成本单元知识体系的结构化梳理任务。例如,在“基础知识”方面运用概念图完成函数、一次函数、正比例函数概念、k与b的含义、一次函数图象的性质、一次函数与一元一次方程关系等内容的梳理,明确概念之间的关系。在“解题技能”方面运用思维导图梳理选择题、填空题、解答题等题型,以及排除法、特殊值法、数形结合法、函数与方程思想等,尤其列出典型习题,展示解题的关键步骤,为以后的解题带来明确指引。
五、单元训练——重点知识的结构化拓展
基于“一次函数”单元的结构化教学,既要注重基础知识的夯实,又要通过单元训练活动的合理设计和有效组织,对重点知识进行结构化拓展,深化学生的认知,拓宽学生的视野,发展学生的数学核心素养。在单元训练中,教师应基于教学内容的结构化分析结果,把握各节知识的外延,精挑细选训练习题,使学生通过做题后的反思、重点知识的分析获取新的知识,将新知识作为对教材重点知识的有效补充。在课堂训练时,教师可以围绕图1中的重要概念、重要性质、重要能力设计习题。针对重要概念,教师可以联系学生的知识储备创设相关问题,要求学生判断参数之间是否是函数关系,通过作答使学生认识到在函数有意义的前提下,自变量x和因变量y的关系为:一个自变量x只能对应一个因变量y,而一个因变量y可对应多个自变量x。针对函数性质可以给出不同函数图象,要求学生比较k值的大小,使其认识到当k > 0时,k值越大,一次函数图象的倾斜程度越大;当k < 0时,k值越小,一次函数图象的倾斜程度越大。针对重要能力可以创设分段函数相关问题情境,提高学生在不同自变量范围下分析问题的意识与能力。
例如,在单元训练中围绕“函数”这一重要概念,教师可以借助网络查询相关题库资源,优选练习题,创设以下问题情境:向一个球形容器中注水,发现水面的高度h、水面的面积S和注水量V为三个变量。(1)S是V的函数;(2)V是S的函数;(3)h是S的函数;(4)S是h的函數。上述说法中有哪些是正确的?该训练习题主要考查学生对函数概念的理解程度。习题(1)中一个变量V只对应一个S,正确;习题(2)中由于球形容器是对称的,S和V并不是一对一关系,错误;习题(3)中一个S对应两个h,错误;习题(4)中一个h对应一个S,正确。该单元练习题从实际情境出发进行设问,引导学生重新审视函数概念,将之前自变量x和因变量y“一对一”的关系,拓展至“一个因变量y可对应多个自变量x”的关系。如此既延展了学生的学习深度,又可以为学生以后更好地学习、理解二次函数打下坚实基础。实践中,教师应结合实际情况,采用同样的方式、方法,抓住单元训练的良好契机做好重点知识的结构化拓展。
“一次函数”这一单元知识在初中函数学习中起着承上启下的重要作用。教师应认识到围绕这一章开展结构化教学的必要性,理顺结构化教学与提高课堂教学质量、满足《标准》要求与核心素养培养之间的关系,做好教学环节的认真设计,尤其在实践中把握教学的关键、细节,推动结构化教学有序、高质量进行。
基金项目:黑龙江省教育科学“十四五”规划2023年度重点课题——新课标理念下的初中数学学科结构化单元整体教学(JJB1423031)。
参考文献:
[1]李圣红. 聚焦结构化教学构建高效初中数学课堂[J]. 试题与研究,2023(1).
[2]苏伶俐. 初中数学知识结构化教学策略探析[J].读写算,2022(28).

