泊松亮斑演示实验的数值研究

张 鑫

(天津职业技术师范大学 理学院,天津 300222)

泊松亮斑是由于衍射而产生的光学现象:当平行光垂直照射小圆屏时,接收光屏的中心会出现一个小的亮斑。这种与常识相悖的现象由泊松于1818年根据菲涅耳子波相干叠加原理推导得出。泊松原本借此反驳光的波动说,但随后菲涅耳从实验上证实了这一亮斑的存在,使之反而成了光具有波动性的明证[1]。这一戏剧性的发现,以及违背“常理”的实验现象,使泊松亮斑在“大学物理”课程的“波动光学”章节中,经常被用来说明光的衍射。将它作为典型的演示实验在课堂中展现,可使学生对光的波动性有直观的认识,提高课堂的积极性和参与度,在激发学生兴趣的同时,也培养了学生对科学真理的探索精神。已有文献报道典型波动光学实验的数值模拟[2-4],以及泊松亮斑演示教具的制作[5-8]。文献[8]用激光结合透镜扩束照射不透光圆屏,在屏幕上获得泊松亮斑。文献[4]利用数值模拟,从半导体微纳加工的角度系统讨论了圆屏尺寸和距离对衍射图样的影响,圆屏尺寸在微米量级,入射光波长主要讨论了紫外波段。为了更好的课堂演示效果,有必要讨论肉眼可见大小的光屏和可见光波段的圆屏衍射。

对圆屏的衍射图样进行了数值计算,并分析了实验各参数对泊松亮斑的影响,包括入射光波长、圆屏尺寸、圆屏与接收屏间距,以及圆屏边缘的光滑程度对衍射图样的影响。这些理论计算结果可以为后续制作泊松亮斑演示实验装置提供理论指导。

1 衍射积分公式及数值结果

圆屏衍射装置如图1所示。衍射屏上任一点Q在接收屏上的正投影记作Q′,z为衍射屏与接收屏间距离。

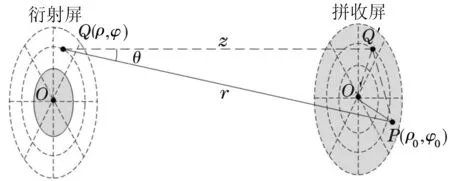
图1 圆屏衍射示意图

根据菲涅耳-基尔霍夫衍射积分公式,极坐标下接收屏任一点P′处的光场分布为[9]

(1)

其中,λ为入射光波长;k=2π/λ,E(ρ,φ)为入射光在衍射屏处的光场分布;r为衍射屏上源点Q与接收屏处观察点P′之间的距离,θ为衍射屏源点Q处的法线与r之间的夹角。(1)式中cosθ和r可在直角三角形QQ′P′中求得,其中的直角边Q′P′可在三角形O′Q′P′中利用余弦定理得出。本文采用垂直入射的单色平面波,即E(r,j)=1,计算出的圆屏衍射图样如图2所示。

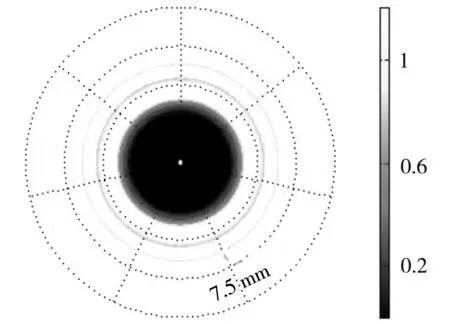
接收屏半径7.5 mm,λ=632 nm,R=2.5 mm,z=2 m

其中,入射光波长为λ=632 nm;圆屏半径为R=2.5 mm;接收屏距离圆屏z=2 m。由衍射图样可以看出,在圆屏的正后方即接收屏的中心位置,出现一个小亮斑,即泊松亮斑,这是衍射屏处光场各子波发出的球面波相干叠加的结果。在圆屏阴影边缘周围分布着亮暗相间的圆环状衍射条纹。图中黄色区域显示背底光强为1,这是由于入射光设置为理想的无限大平面波(振幅为1),没有被圆屏遮挡的部分直接照到了接收屏。

影响泊松亮斑演示效果的有亮斑的强度、亮斑的大小以及亮斑与周围阴影区的对比度,我们分别用参数I0、D、V来衡量。其中,I0是用入射光归一化的中心点光强;D是亮斑直径,即亮斑两侧光强极小点的间距;V是亮斑对比度,定义如下:

(2)

其中,I0是中心点光强;Im是泊松亮斑周围阴影区的光强最小值。这三个参数(I0,D,V)均可通过圆屏衍射图样的光强分布求出。例如,在图2所示的参数下,I0=1,D=0.5 mm,V=1。

2 各参数对泊松亮斑的影响

2.1 入射光波长

图3为可见光范围内,入射光波长分别为450 nm、532 nm和632 nm(可分别用氩离子激光器、半导体激光器和氦氖激光器实现)的圆屏衍射图,圆屏半径均为2.5 mm,圆屏与接收屏距离均为2 m。由图可知,这三个波长的衍射图样区别不大。定量来看,它们的中心点光强I0均为1,对比度V也均为1。红光波长更长,衍射效应更明显,光斑直径D略大于绿光和蓝光(红光D≈0.5 mm,绿光D≈0.4 mm,蓝光D≈0.35 mm)。设计演示实验时,在上述参数下,可根据已有的实验条件任取一种激光器。

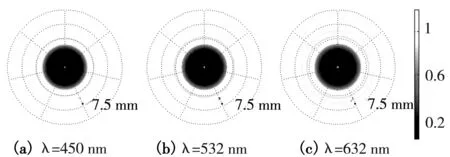
接收屏半径7.5 mm,R=2.5 mm,z=2 m

2.2 圆屏半径

改变圆屏的尺寸,得到衍射图样,如图4所示。图中固定入射光波长为632 nm,接收屏距圆屏2 m,分别计算了圆屏半径依次为0.5 mm,1.5 mm,2.5 mm,3.5 mm,4.5 mm,5 mm的衍射图样。显然,圆屏尺寸越大,阴影区域越大,而不论圆屏尺寸如何变化,接收屏中央均出现亮斑。与圆孔衍射不同,圆屏衍射图样的中心点并不会出现亮暗交替的变化。根据半波带理论,圆屏衍射中央亮斑的合成振幅可用式(3)表示[9]:

(3)

其中,k是圆屏对接收屏中心遮挡住的半波带个数;ak+1是第k+1个半波带在中心点产生的振幅。k值可以用式(4)计算[10]:

(4)

其中,R为圆屏半径;λ是入射光波长;z是圆屏与接收屏间距。理论上,圆屏尺寸越大,k越大,ak会随倾斜因子的增大缓慢减小,中央亮斑的强度会有所下降。在图4的参数下(z=2 m,λ=632 nm,R=0.5 mm～5 mm),根据公式(4)估算出圆屏遮挡住的半波带个数为0.2～20个。而ak只和倾斜因子有关[9],a1与a21的差别很小,可以忽略,因此图4所示中心点的光强值在不同圆屏半径下始终为1。经估算,当k达到z/λ的量级(约106)时,ak+1与a1的差别才不可忽略,中心点光强I0开始变弱。而用于泊松亮斑演示的圆屏半径R通常为mm量级,对于理想圆屏,在此范围内改变R不会影响泊松亮斑的强度。

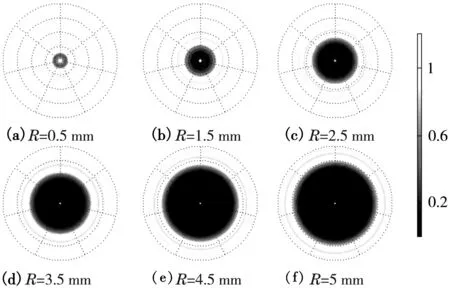
接收屏半径7.5 mm,λ=632 nm,z=2 m

图4显示,随着圆屏半径的增大,亮斑的直径D减小。这一变化关系可作如下定性解释:圆屏边缘两点到光斑边缘的光程差从几何关系出发可用2Rsinθp估算,其中θp是光斑对圆屏中心所张半角,可用D/2z估算,因光斑边缘为光强极小值,此光程差还可用D/2估算,可得光斑直径的估算式为

(5)

可知,光斑直径D随R的增大而减小,随波长的增大而增大,后者已在2.1节得到了验证。需要注意的是,此式仅可定性分析光斑直径D随各参数的变化关系及量级,无法定量确定光斑大小。

虽然图4(a)的光斑直径最大,但周围光强较强,即对比度较低,不能达到很好的演示效果。为此,图5计算了泊松亮斑的对比度V随圆屏半径R的变化曲线。

R/mm

由图5可知,随着圆屏半径R的减小,衍射效应更明显,屏边缘的衍射场叠加到阴影区导致对比度V下降。当z=2m,圆屏半径R<1 mm时(即k<0.8)对比度V开始急剧下降,至R=0.5 mm时已降至V=0.5以下(此时k=0.2)实际上,当泊松亮斑的尺寸达到圆屏的几何尺寸,圆屏后方将没有明显的暗区,即对比度较小。由(5)式,当D与2R相比拟时,k～0.25。因此,要产生对比度好的泊松亮斑需要k不能显著地小于1。当波长λ取500 nm,距离z取2 m,由(4)式可得圆屏半径R须大于1 mm才能观察到明显的泊松亮斑。

2.3 圆屏与接收屏间距

考虑演示实验通常在教室进行,我们将接收屏依次放置在距离圆屏0.5 m,2 m和5 m的位置,并固定参数:入射光波长 λ =632 nm,圆屏半径R=0.5 mm,计算衍射图样,见图6。

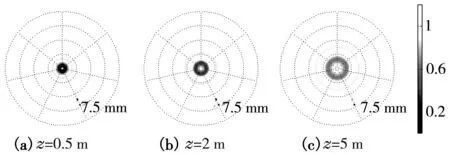
接收屏半径7.5 mm,λ=632 nm,R=0.5 mm

可见,当圆屏与接收屏间距增大时,中心点光强I0不变,而光斑直径D增大。利用公式(4)可计算在图6参数下,各圆屏都没有完全遮挡住第一个半波带((a)k=0.8,(b)k=0.2,(c)k=0.08),因此I0均为1。而由公式(5)可知光斑直径随圆屏与接收屏间距z的增大而增大。当间距z=0.5 m时,光斑直径D=0.5 mm,此时仍可观察到亮斑。

另一方面,随着z的增大,对比度V却在下降。图7计算了泊松亮斑的对比度V随z的变化曲线。

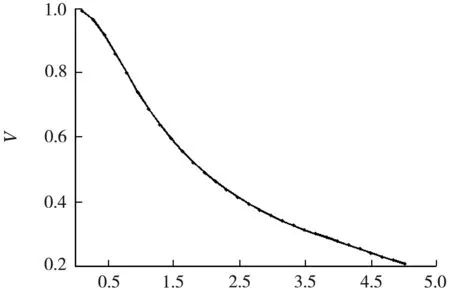
z/m入射光波长λ=632 nm,圆屏半径R=0.5 mm

由图7可知,当圆屏半径R=0.5 mm,z值接近2 m时,对比度V已降至0.5,对应图6(b)的衍射图样。根据2.2节的讨论,此时k=0.2,圆屏与亮斑的尺寸可比拟,衍射图样已不利于演示。

2.4 粗糙度

考虑到实际的圆屏并不是严格的光滑圆屏,在屏边缘处会存在一定的粗糙度。本文在圆函数基础上叠加正弦函数模拟粗糙的圆屏,可得圆屏半径R为

R=R0+r0sin(nφ) ,

(6)

其中,R0为光滑圆屏的半径;φ为衍射屏上边缘一点P′的极角;r0定义成粗糙度振幅;n定义成粗糙度频率。改变粗糙度的振幅r0和频率n,计算接收屏中心点处的光强,结果如图8(a)、(b)所示,

由图可知,粗糙度的频率对中心点处光强没有影响,而增大粗糙度的振幅会使泊松斑的强度减弱。固定粗糙度频率n=20,改变粗糙度振幅r0,当r0=0.07R0时,泊松亮斑强度降为光滑圆屏的0.5倍以下。振幅r0在不同取值下的衍射图样见图8(c)～(e)。当振幅r0<0.07R0时,衍射图样仍可见明显的泊松亮斑,见图8(c);r0>0.07R0时,I0降到0.5以下,泊松亮斑不易观察,见图8(e)。

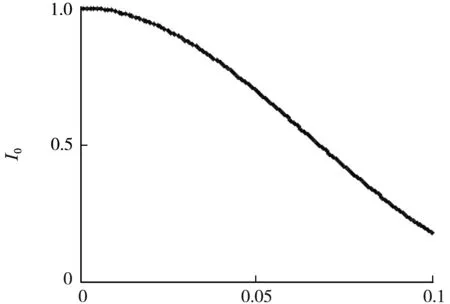
r0/R0(a) n=20

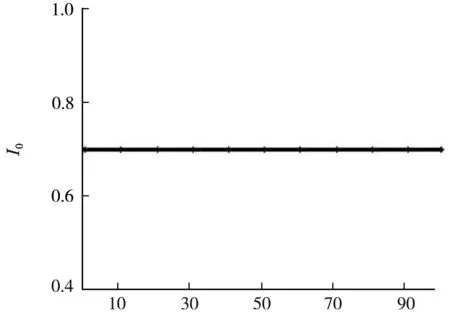
n(b) r0=0.1R0

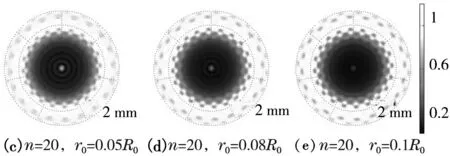
接收屏半径2 mm,λ=632 nm,R0=1 mm,z=0.6 m

图8的结果也可利用半波带法定性解释。起伏的边缘将衍射屏分成两部分:完全遮挡区域(圆屏部分),部分遮挡区域(圆屏粗糙边缘部分)。其中部分遮挡区域构成内外径分别为R0-r0和R0+r0的圆环,此圆环覆盖的半波带个数k'由公式(4)计算得出:

(7)

其中,k为半径为R0的光滑圆屏覆盖的半波带个数。根据图8(e)的参数,当振幅r0=0.1R0,R0=1 mm,z=0.6 m时,k′≈1,即部分遮挡区域覆盖了第一个露出的半波带。将正弦波简化成方波,则此半波带振幅减半,相应的矢量叠加图如图9所示。

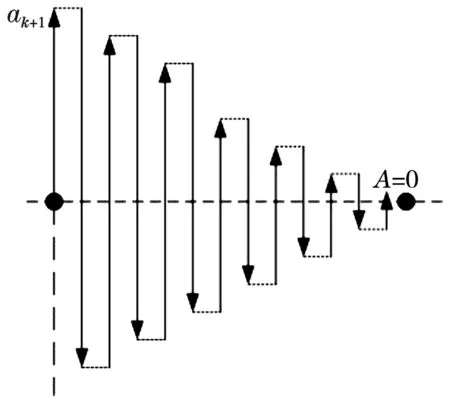
图9 边缘半波带被方波遮挡的矢量叠加图

由于ak+1减半,导致合振幅由ak+1/2变为0,对于正弦波情况较复杂,合振幅不会降为0,但变化趋势相同,即粗糙度振幅的增大会导致亮斑光强I0减弱,见图8(a)。而粗糙度频率n的变化不会影响这种振幅减半的效果,因此I0不随n改变,见图8(b)。

通过对比图8(c)～(e),可知粗糙度振幅对亮斑的直径影响不大,且阴影区光强极小值均达到了0,V的计算值始终为1。所以,当圆屏边缘叠加粗糙起伏时,制约泊松亮斑观察效果的主导因素是中心点光强I0。设计实验时,应注意控制圆屏边缘的粗糙度振幅r0,即要求粗糙区域不要超过一个半波带,根据公式(7),可用r0/R0<1/(4k)估算。可见,k越小,对圆屏光滑程度的要求就越低,当k<0.25时,圆屏边缘的起伏不会对亮斑光强造成影响(但此时对比度会变弱,见2.2节)。对于粗糙的圆屏,要看到泊松亮斑需对k,从而对R0提出要求。例如,当r0=0.01R0,λ=500 nm,z=2 m时,要求R0<5 mm才能观察到明显的泊松亮斑。

3 结 论

对圆屏衍射图样进行了数值计算,并分析了光源波长λ、圆屏半径R、圆屏和接收屏间距z以及圆屏粗糙度对泊松亮斑的影响。计算结果显示,圆屏对接受屏中心遮蔽的半波带数k是影响泊松亮斑的重要参数,k远小于1时,亮斑的对比度过低,不利于观察;k过大时(>106),亮斑的光强变弱,不利于观察;k适中时,亮斑的光强(用入射光归一化)和对比度都接近1,亮斑大小可粗略用(5)式即R/(2k)估计其量级。过于粗糙的圆屏也不宜于泊松亮斑的实验,当屏的边缘起伏超过一个半波带,即r0/R0>1/(4k)时,不利于观察泊松亮斑。因此,在k值适中,保证I0=1,V=1的前提下,k越小,亮斑直径越大,对圆屏边缘光滑程度的要求越低,越有利于演示。