全反射法测量液体折射率的一种改进方案

杨江萍,张员铭,邱佩惠,周卫东,汪 成

(北京邮电大学 理学院,北京 100876)

折射率是液体重要的光学参量,与液体的多种物理性质密切相关,对其进行精确测量在食品、化工、医药等诸多领域有着重要意义。目前常见的液体折射率测量方法[1-4]从原理上大致可分为两类:一是以几何光学为基础的角度测量法,如全反射法[5]、掠入射法[6]等;二是通过测量透射光或反射光的光学特性得知介质折射率的方法,如椭偏法[7]、干涉法[8]、光栅衍射法[9]等。其中,棱镜组全反射法操作简单、精度较高、所需待测液少,适于快速精确测量透明液体折射率。

本文在传统的棱镜组全反射法[10]基础上,提出了一种基于激光器的实验改进方案,通过采用单一波长的光源提高了测量精度,便于观察实验现象,通过自动化改进,在普通大学物理实验室即可实现,便于实际应用与推广。

1 实验部分

1.1 实验原理

棱镜组全反射法的基本原理如图1所示。将一对三棱镜如图平行放置,在相贴合的两个光学面之间加入待测液体薄膜。

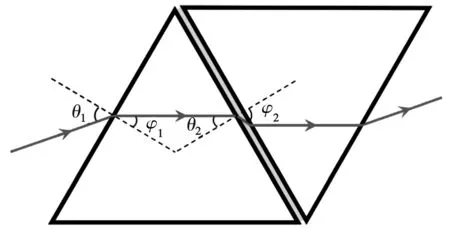
(a)

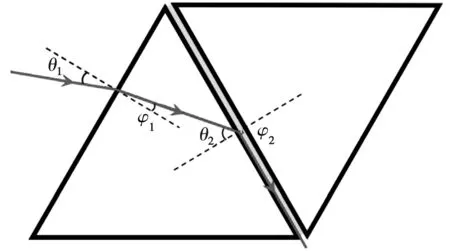
(b)

由折射定律可知:

sinθ1=n0sinφ1,

(1)

n0sinθ2=nsinφ2,

(2)

φ2+θ2=60° 。

(3)

如图1(a)所示,当改变入射角的大小时,根据光路的对称性原理,出射光方向始终与入射光方向相同。而当入射角逐渐减小至某一特定角度θ1时,在棱镜的光学面和待测液体的界面上发生了全反射现象,如图1(b),出射光方向产生消光现象。由于液体薄膜很薄,可以认为此时的φ2=90°,代入(1)(2)(3)式可得待测液体折射率的计算公式:

(4)

其中n0是三棱镜玻璃的折射率,可由最小偏向角法[11]等测得,因此只需要测量出全反射时的入射角θ1,就可以计算出待测液体的折射率。

在传统的棱镜组全反射法中,一般采用复合光源如:汞灯、钠灯等。在实际的实验观测中,发现采用复合光作为光源时,各种波长的光混在一起,实验现象并不明显。由于出射光的消失是一个连续的过程,即某色谱线发生消光时望远镜中会观测到对应互补色亮线,改变入射角时视野中所见为先连续变色、最终谱线消失的过程,所以使用复合光源会使实验产生误差。因此,采用单一波长的激光器做为光源,对实验装置进行了改进。为了解决激光不能用肉眼观察的问题,我们在分光计望远镜端安装了摄像头,以电脑作为观察屏,这不仅使得实验现象更便于观察与记录,同时还提高了测量的精度。

1.2 实验过程

我们的实验改进装置如图2所示,主要包含:JJY型分光计、激光器,三棱镜组、摄像头及电脑等。

图2 实验装置实物图

下面以650 nm红色激光为例介绍实验操作。

准备工作:首先将分光计调节到工作状态,并在望远镜安装摄像头,将电脑与摄像头连接,利用电脑屏幕观测实验现象。挑选折射率相同的两块三棱镜Ⅰ和Ⅱ,如图1所示紧贴放置在载物台上,这时要求载物台的高度可以使所有入射光都进入三棱镜,从而消除入射光从棱镜组上方直接射入望远镜对消光现象产生的干扰。调整棱镜组合的中心与载物台中心重合。判断标准为,当旋转载物台改变入射角时,出射光线位置不发生改变,则说明棱镜组合的中心与载物台中心重合。

全反射现象的观测和入射角的测量:在三棱镜Ⅰ和Ⅱ之间加入液体,挤出气泡,形成薄膜。这时从观察屏中可以观测到一条亮线,如图3(a)所示。缓慢旋转载物台逐渐减小入射角θ,因为光路具有对称性,亮线并不移动。继续旋转载物台,使得入射角达到临界值θ1时,亮线恰好消失,表示此时发生了全反射,此时停止旋转载物台,同时保持三棱镜不动。由于两块三棱镜Ⅰ和Ⅱ的折射率相同,考虑系统的对称性可知:出射光与法线的夹角等于入射角,因此测量发生全反射时的出射角φ即等于此时入射角θ1。由于出射光并不随着入射角的改变而移动,故在观测时就可记录其所在位置θ1,从左右游标上读出望远镜在位置θ1的读数φ1左和φ1右。再旋转望远镜观察三棱镜Ⅱ,当绿色反射十字像竖线和望远镜黑色叉丝重合时为三棱镜Ⅱ的法线方向θ2,如图3(b)所示,从左右游标上读出望远镜在位置θ2的读数φ2左和φ2右,代入公式(5)即可计算出θ1。

(5)

这时根据公式(4)我们便可以求算出液体的折射率。

图3 实验现象

2 结果与讨论

2.1 测量结果

利用最小偏向角法测量出在实验所用的三棱镜中对不同波长光的折射率,再将实验所得数据代入公式(5)得出θ1测量值,最后将上述数值代入公式(4)计算出不同波长的光在纯净水中的折射率n并与标称值比较,结果如表1所示。

可以看出,用该方法测量不同入射光波长情况下水的折射率时均保持了较高的精度,相对误差保持在0.2%以内。折射率的测量值相较参考值整体偏高,经分析应为实验室环境温度较低所致。

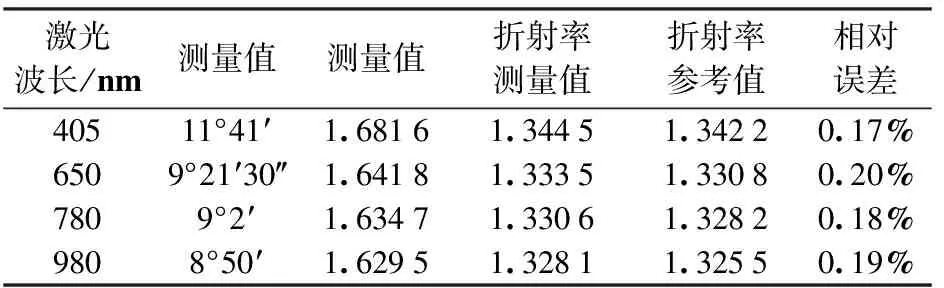
表1 纯净水在不同光波长下的折射率测量结果

类似地,若换用不同液体形成液膜进行全反射角θ1的测量,再将有关量代入公式(4),则可求出该液体在对应情况下的折射率,如表2所示。

表2 不同液体在650 nm波长光下的折射率测量结果

由表2可见,实验所测得的不同液体折射率的数据与参考值基本吻合,说明该方法对于各种透明液体折射率的快速精确测量均可适用。

2.2 误差分析

由公式(4)可知,测量结果的精度取决于n0以及θ1的测量精度。可以算出:

(6)

以纯水对650nm光的折射率为例。六次重复测量全反射角θ1所得结果如表3所示。

表3 纯净水对650 nm波长光的全反射角测量结果

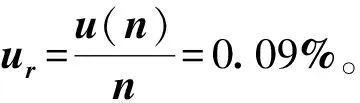
2.3 等倾干涉的影响

当薄膜厚度均匀时,以倾角入射的光线在薄膜界面多次反射后从对侧出射,其反射次数不同的光会发生等倾干涉。由于透明液体和玻璃反射率较低,可仅考虑在液膜内缘反射两次的透射光与原光场的双光束干涉,如图4所示。

图4 等倾于干涉示意图

当入射角θ接近全反射角θ1时,光在界面的反射率增大,摄像头观测到谱线出现轻微明暗交替变化的现象,最后在θ=θ1时消失,如图5所示。而在实际测量中,由于激光器光强很大,谱线变暗时仍有较强的光强,与消光现象有着很大的区别,因此很容易进行辨别,对于实际观测谱线消失现象的影响可以忽略。

(a)

(b)

(c)

(d)

3 结 论

本文引入激光器和摄像头以改进原有测量液体折射率的实验方法,既提高了测量的精确度,又简化了现象观测。实际操作测量所得数据与文献理论值基本吻合,在对实验系统进行了误差分析后,确认测量结果是精确有效的,由此证明文中的测量方法行之有效。

文章所述实验方法系统简单,观测方便,所需待测液体少,可用于各种透明液体折射率的精确测量,填补了普通大学物理实验室快速测量液体折射率的空白。摄像头这一装置的引入既方便了实验现象的观测和演示,又拓宽了可用于测量的光波长范围,同时也为分光计的教学改进提供了一条新思路。

此外,由于激光的方向性好,能量集中,因此未来也可以考虑不使用分光计,而是采用更简单的装置,结合光敏器件来实现液体折射率的自动化测量。