弗兰克-赫兹实验中电流变化的研究
张 顺,易庭丰,吕宪魁
(云南师范大学 物理与电子信息学院,云南 昆明 650500)
弗兰克-赫兹实验,有力地证明了能级的存在。其原理是热阴极放出电子,在阴极管中设置加速电场,并充入汞蒸气,电子通过加速电场,携带一定的能量与汞原子碰撞,当电子能量为汞原子第一激发势能的整数倍时,电子因将能量传递给原子而无法达到接收板,使电流呈现出周期性的起伏。
在近现代,学者对该实验的研究从未停止,其中最多的是研究第一栅极电压[1]、减速电压、灯丝电压[2-5]等因素对实验结果的影响,以期获得最佳实验条件[6-12];在教学方面,何彪[13]等人也做了一些尝试;闫志巾[14]等人也在尝试着开展线上结合线下的教育模式。李文韬等人基于LabVIEW平台,开发了虚拟仪器,这使得该实验更加便捷[15]。ROZHKOV IL′JA STEPANOVICH应用弗兰克-赫兹实验中的装置,对氢、氘和氚的含量进行质量和数量估计[16]。
本文在前人的基础上,通过大量的实验,研究得到加速电压和减速电压如何影响实验结果、电子在阴极管中的运动过程;减速电压与导通电压的关系、时间步距对实验图像的影响。在此过程中我们发现一些新的实验现象,并对这些现象进行了一定的解释。
1 电子运动
本实验中所用的器材是ZKY-FH-2弗兰克-赫兹实验仪,其内部的弗兰克-赫兹管可简化为图1所示模型。
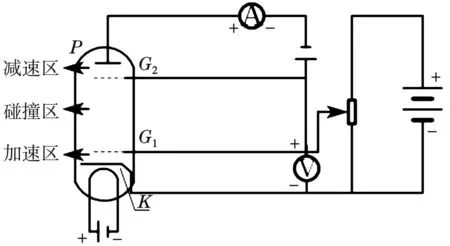
图1 F-H管结构示意图
电子在管内先经过KG1加速,在G2P中被减速后,最终到达P点,形成电流[12]。这种模式,是为了测量更高能级而设立的。在测量第一激发势时[1,17],加速区为KG2。当电子到达G2处的能量小于qUG2P时,由于具有初动能,电子会在加速区的上部分和减速区发生振荡,当电子在G2处的能量大于等于qUG2P时,这种振荡才会结束。这种效应,文献[18]将其类比为电阻,而值得注意的是:减速区的“电阻”与减速电压UG2P不是线性关系。
2 电子运动实验验证
2.1 问题提出和实验现象
在同一实验条件下,电流强度随着减速电压增大而减小。为了探究减速电压和电流是呈现怎样的数学关系,我们得到图2:当其他条件一定时,电流强度与减速电压呈现负相关。
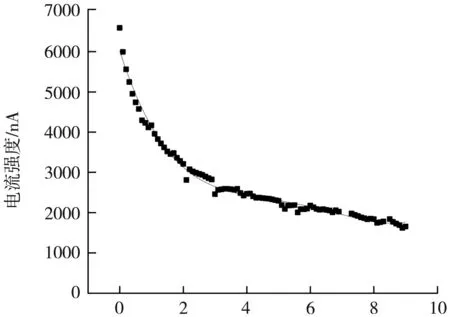
减速电压/V
在处理数据时,我们发现无论加速电压为何值,图2所示关系均存在,且通过数值分析,拟合模型为y=ax4+bx3+cx2+dx。在研究加速电压对实验结果的影响时,该关系仍然存在。
2.2 可能的解释
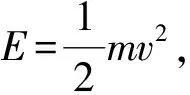
(1)
t1时刻,电子将进入加速区,此时加速电压为U1=Ut0+nt1,电子在加速区先做减速运动,速度减至0后,再加速重新进入减速区。电子在加速区的加速度为
(2)
解得电子速度减为0所需时间t是一个包含t1和Ut0的数,由此得到电子在加速区走过的路程为
L=vt-αUt0t2-βnt3,
(3)
其中α和β是常数;t时刻的加速电压U2=U1+nt,假设电子在经过加速区后就足以通过减速区(即假设从此时开始,加速电压不再变化,电子都能通过减速区。若电子不能通过减速区,则重复上述内容),则电子获得的能量为
(4)
将L带入后,得到
Ek=at4+bt3+ct2+et。
(5)
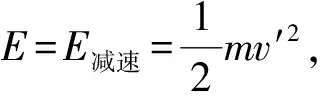
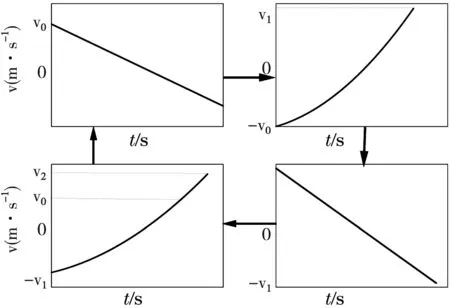
图3 电子速度变化示意图
这证明了电子在F-H管中是存在振荡的,该振荡影响电子能量变化的快慢,进而影响单位时间内通过减速区的电子数量。
3 减速电压对实验的影响
3.1 减速电压对实验图像的影响
由于减速电压的存在,使得能量不同的电子到达接收板的时间不同,这便起到了选择电子的作用;在实验中,这体现为相同的实验条件下,不同的减速电压,电流信号不同。如图4所示,当减速电压增大时,相同条件下,电流强度会降低;同时导通电压(即开始检测到电流时的加速电压)会增大。这因为电子要通过减速区形成电流,其自身携带能量必须满足条件:Ek≥qU减。因此当减速电压增大时,电子所需的能量随之增加,则表现为所需加速电压增大。综合上述内容,减速电压增大,会使得实验曲线整体向导通电压增大、电流减小的“右下”方向移动。
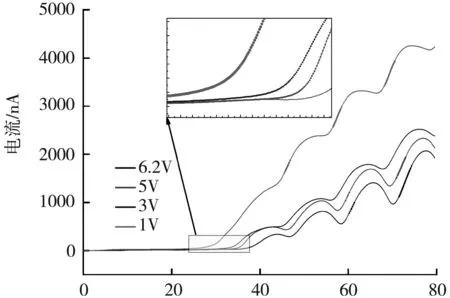
电压/V
3.2 减速电压对导通电压的影响
根据3.1所得结论,导通电压和减速电压发生同向变化。两者关系如图5所示。
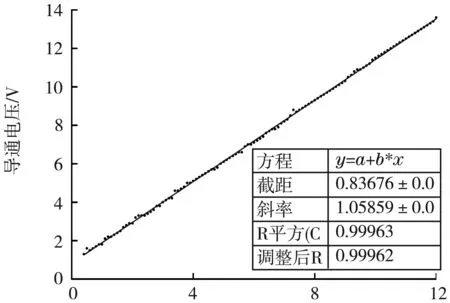
减速电压/V
导通电压与减速电压之间呈现正比关系,但比例系数大于1,意味着减速电压的变化量小于导通电压的变化量。这表明在电子运动的整个过程中,除外加的减速电压外,可能还存在着其他使电子减速的场U=U-U=0.057U减。作导通电压与减速电压的差值随减速电压变化图像,如图6所示:两者差值随着减速电压呈现出阶梯状上升。考虑到实验中,加速电压只能以0.1 V为间隔变化,即理论直线只能显示0.1的整数倍,如图6中的“显示差值”所示,处理得到的差值如图6中“实际差值”所示,“实际差值”与“显示差值”相同。发现两者吻合度高,可说明差值的阶梯状上升是由于仪器本身引起的,并不是一种“量子现象”。
而针对导通电压变化量大于减速电压变化量,根据上文中2.2中的解释,可能是由于电子在到达接收板之前发生振荡,使得部分加速电压并没有作用在电子上,而使导通电压变大。
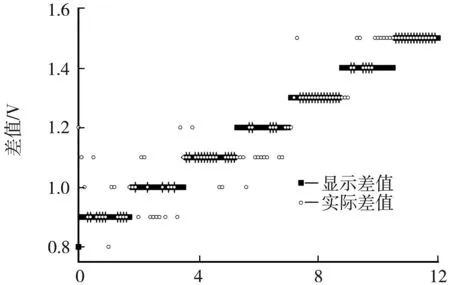
减速电压/V
同时在图5中我们发现拟合的直线存在纵截距。这说明在不设减速电场的前提下,电子仍需要向外界“索取”能量,以便到达接收板。综合F-H管的结构看,纵截距包含了空间电荷、接触电势差等信息。
4 栅极电压对电流的影响
阴极K附近聚集着大量的电子,这会使得阴极发射出的电子受到阻滞而无法参与形成电流。第一栅极电压的主要作用是驱散热阴极及空间中的带电体,减小空间电荷对电子的干扰。由此可见,栅极电压对电流是有影响的,根据文献[1],栅极电压对电流存在促进作用。保持其他条件不变,改变第一栅极电压,结果如图7所示。
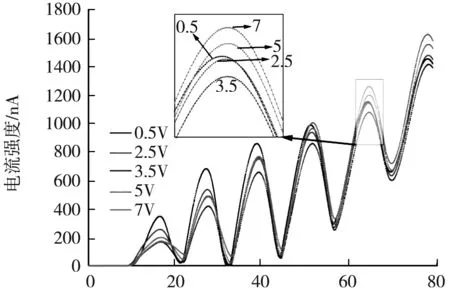
电压/V
从图7中可看出,栅极电压对电流不仅有促进作用,还存在抑制作用,文献[6]中对该问题的解释是:电子与原子间存在着相互碰撞,当电压越大时,空间电荷被驱散的同时,也将电子能量提高,加大了碰撞的可能性,所以使得电流减小。按照该解释,栅极电压越大,则电流会一直降低。
保持其他实验条件不变(其中加速电压变化范围为0~80 V,幅度为0.1 V),以0.5 V为间隔,使栅极电压从0 V均匀变化至12 V。每改变一次栅极电压,进行一次实验,共实验24次,研究每一个加速电压下,栅极电压与电流强度的关系。具体如图8所示:上部分图是不同加速电压下,栅极电压对电流的影响情况(一共700条曲线,图中给出4条不同加速电压下的栅极电压-电流强度曲线)。我们发现电流在一些栅极电压下,出现下降的情况,现将每一条栅极电压-电流强度曲线中出现局部最小电流的点提出,绘制成图8下半部分图像;通过该部分图像,可以发现,电流的下降不是“偶然事件”,几乎所有的电流,在一些特定的栅极电压下都发生下降情况。
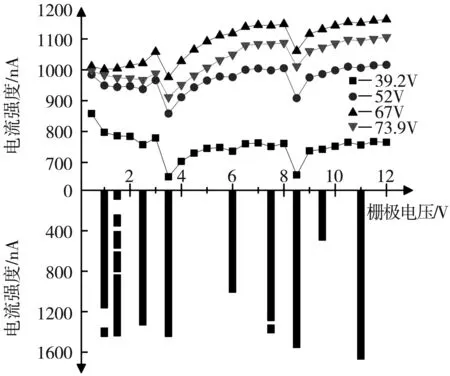
图8 栅极电压对电流起伏的影响
若按照文献中的解释,电流即使出现下降,但由于栅极电压在增大,整体应当呈现上升趋势。很显然与实验事实不符。在图8上部分图中,我们发现在3.5 V和8.5 V时电流下降最大,而其他的下降幅度相对较小。除去这两处特殊点,以栅极电压6 V为分界线,相邻下降电流所对应的电压差值约为1.5 V。在此我们认为,电流的减小除了碰撞,可能还存在着其他的物理过程(尤其是在3.5 V和8.5 V两处下降明显的位置),相关问题,仍在进行进一步的研究。
同时我们还发现,栅极电压对不同加速电压下的电子的作用结果也是不一致的,如图9所示。
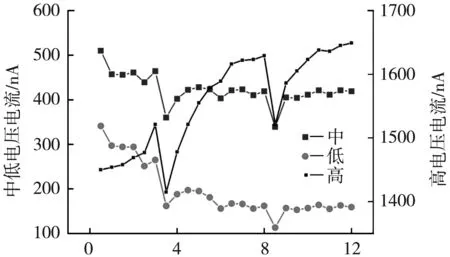
栅极电压/V
对低加速电压下的电子,电流整体呈下降趋势;中等加速电压下呈现基本持平;对高加速电压呈现出整体上升趋势。对此可能的解释是:形成电流时,在不考虑电子与原子碰撞的前提下,电子的能量应该为E=q(U栅极+U加速-U拒斥);我们认为三种情况产生的原因与加速电压提供能量和电子碰撞减少能量的量级有关。在低等水平的加速电压下,加速电场提供的能量较小,其量级比电子损失能量的量级小,所以损失能量相对较多,因此呈现出整体下降趋势;而当栅极电压到中等水平时,加速电压所提供的能量与电子碰撞损失能量可比拟,则呈现出平稳趋势;当达到高等水平时,加速电压提供能量远大于电子碰撞损失能量,所以整体呈现上升趋势。
5 时间步距对实验的影响
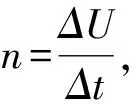
5.1 时间步距对电流强度的影响
时间步距对电流的影响见图10。
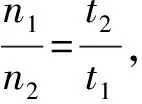
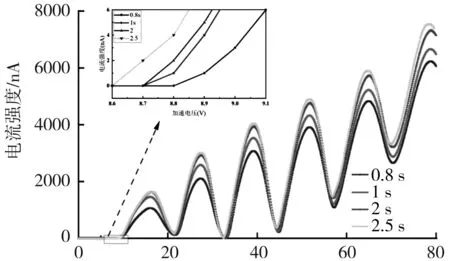
加速电压/V
该结论也可由(2)式得出:时间步距越大,n值越小,则在加速区的速度变化慢,使得电子在F-H管中振荡次数增加,电子积累量增大;当加速电压达到一定值时,使得电流增大。
5.2 时间步距对导通电压的影响
从图10中还可以看出,不同的时间步距下,导通电压也不相同,在进行多组实验后,得到如表1所示数据。
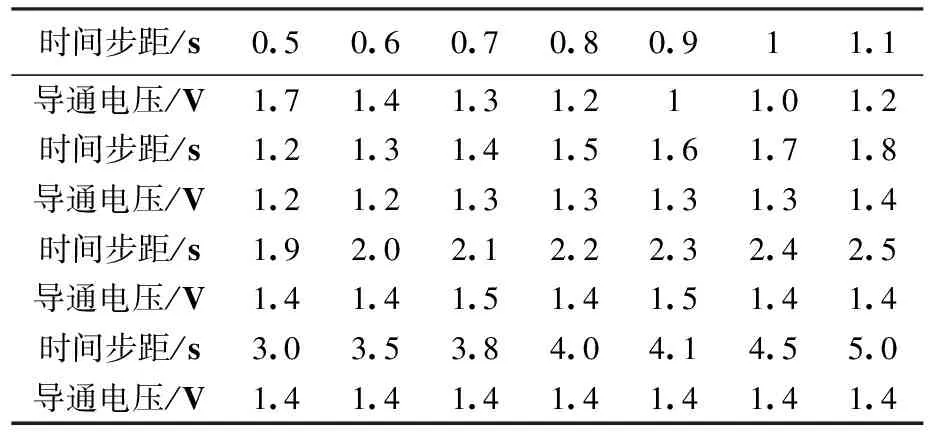
表1 不同时间步距下的导通电压
关于时间步距如何影响导通电压这一问题,我们还在做进一步研究。
6 结 论
本文推导了电子在F-H管中的运动情况,发现电子在F-H管中可能存在着振荡,并给出了电子在管中的振荡过程。减速电压、栅极电压、时间步距影响电流强度的机制一致:影响电子的振荡。此外,本文还发现在一些特定栅极电压(3.5 V和8.5 V)下,电流强度会出现大幅度的下降;时间步距在一定程度上会影响导通电压的大小。在此基础上,可以更好地理解F-H管中的电流形成原理、电子运动情况和电流变化机理,进而找到更好地实验参数,这对实验教学有一定的启发。

