基于回音壁微球腔的共振现象实验教学设计研究

于 琦,缪 琦,吕 亮

(安徽大学 物理与光电工程学院,安徽 合肥 230601)

在全国大力推进高等教育“双一流”建设的新时代背景下,高等教育改革鼓励教师在实验教学中更多地引入科学问题,将科研成果或自己所熟悉的前沿课堂及时转化为实验教学资源,不断更新和充实实验教学内容,使实验教学的内容更具新颖性和先进性[1,2];与此同时,使学生实验过程贴近实际、贴近前沿,真正实现学有所思和学以致用,符合“以学生为中心”的课程思政目标[3,4],对培养学生创新意识和能力研究具有重要意义。

在大学基础物理学习中,学生对共振现象的理论知识可以较容易掌握,但对生活实践应用中的共振现象思考较少,而涉及共振现象的大学物理实验大多以节拍器共振、小球单摆运动等简单的实验案例教学,教学内容略显陈旧。为保持教学内容的先进性及前沿性,在实验教学中,开发了“基于回音壁微球腔的共振模式实验测量”教学实验,通过将学科前沿研究课题与基础物理知识的有机结合,不仅激发学生的创新性思考,提升利用所学知识与技能解决问题的能力,同时起到促进实验教学内容不断改革和创新的作用。

1 理论原理

光学微腔是一种能够将光场限制在极小空间区域内的光学系统[5],所局域的光场通常具有很高的光能量密度和特定的光场分布。科研人员基于光学微腔先后开展大量关于光与物质强相互作用的基础物理研究[6],以及光学微腔激光器[7]、滤波器[8]等新型光电子器件的基础应用研究。其中基于回音壁模式的光学微腔是近20年来研究最为广泛的一类光学微腔。回音壁现象最早是由Lord Rayleigh在1910年于英国伦敦的圣保罗大教堂研究声波现象时首次发现并提出,他发现声波可沿着大教堂圆弧形墙壁传输,站在墙壁附近可清晰地听到相距很远处的两人谈话,所以这种现象被称为“回音壁模式”[9]。

球形的回音壁微腔(后文称微球腔)具有较高的品质因子,较小本征损耗,当满足特定的谐振条件[10]时,即:

mλ=2πRneff,

(1)

其中,m为回音壁微球腔的角向模式数,λ为共振波长,R为微球腔赤道面的最大半径,neff为微球腔的有效折射率。光场被束缚在微球腔赤道附近一个窄环带内,所产生的基于回音壁模式的光场能量分布可通过测量光波经过回音壁微腔耦合后的透射光谱表示。这里所满足的“谐振条件”本质上即光波频率匹配微腔的本征频率时产生的一种共振现象。

2 实验设计

测量回音壁模式的方法通常采用微纳光纤-微球腔空间上垂直耦合[11]的方法实现,即将直径1～2 μm的微纳光纤与微球腔的赤道轴垂直耦合,光波经微纳光纤的一端耦合进入微球腔,满足谐振条件的光波在微球腔内来回反射,通过微纳光纤的另一端探测输出光强变化。实验教学中,学生可采用电弧放电法制备微球腔,即光纤末端在电极放电作用下熔融,在重力作用下形成球型的回音壁微腔结构,该方法简单,易操作。如图1为显微镜下观察的直径为60 μm的回音壁微球腔实物图。锥形光纤一般采用氢氧焰加热熔融光纤的方式制备,使直径为125 μm的单模光纤被拉伸成为锥区直径仅有2 μm左右的双锥形微纳光纤,可使得进入微纳光纤的光场较容易在锥区产生倏逝场,进而耦合进入微球腔内。

图1 直径为60 μm的回音壁微球腔实物图

实验教学中通过测量微球腔所激发的回音壁模式透射谱来验证微球腔中的共振现象。一般采用激光扫频的方法实现,即在微纳光纤一端输入激光,使得激光频率在回音壁模式的共振频率附近随时间线性扫描变化,在微纳光纤另一端测量输出激光的透射率在时域上的变化曲线。实验装置如图2所示,包括可调谐激光器(New focus TLD-6700,线宽<200k Hz)、偏振控制器、微腔-光纤耦合系统,砷化镓光电探测器(New Focus 1801,带宽125 MHz)、信号发生器和示波器Keysight MSOS604A,带宽6G Hz)。来自可调谐激光器作的输入光,经过偏振控制器进入微纳光纤,微纳光纤中的光纤与微球腔发生光场耦合,输出光信号经过光电检测器转化为电信号,用示波器进行实时监测。为了使得可调谐激光器的扫描频率与示波器的时域信号采集同步,借助信号发生器产生一个周期性三角波信号,其中一部分施加在激光控制器上用于快速扫频,另一部分和示波器相连用于同步观察回音壁模式的透射谱信号。当三角波施加在激光控制器上时,会驱动激光器内置压电陶瓷产生微小的形变,从而使输出激光围绕特定中心频率快速扫频。三角波信号上升沿(或下降沿)的周期等于可调谐激光器进行激光频率扫描的周期,三角波信号的驱动电压与激光扫描频率的范围成正比。

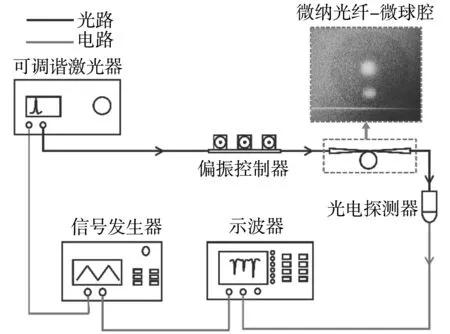
图2 激光扫频法测量共振模式的实验装置示意图

实验具体操作时,通过调节微纳光纤与微球腔的空间耦合距离,使微球腔逐渐靠近微纳光纤的锥区,以激发微球腔的回音壁模式。即当输入光频率逐渐靠近并达到微球腔本征谐振频率值时,满足公式(1)中的谐振条件,可使得微腔内发生共振,此时该频率的光可在腔内发生多次全反射,被局域在该微腔内,而在微纳光纤另一端测得的透射光功率最小,进而在示波器上观察到该频率对应的电压幅值最小;反之,当输入激光频率远离微腔的本征频率时,该频率的光逐渐未被耦合进入微腔,故在微纳光纤输出端测得的输出光强逐渐增加,对应的电压值逐渐增大。该过程在示波器的时间周期内可观察到呈洛伦兹线型的透射峰曲线,如图3所示的蓝色洛伦兹线型的凹陷峰。

实验教学过程中,设置可调谐激光器的中心波长为1 556.42 nm,三角波信号频率为5 Hz,扫描电压峰-峰值为3 Vpp为例,演示示波器上观察到对应的时域信号,如图3所示。其中红色曲线为三角波上升沿的信号;蓝色曲线表示激光频率与回音壁微球腔的本征频率发生共振时的透射光谱,透射谱中下垂的细线是极细的洛伦兹型,代表激光扫描过程中所激发的共振模式。

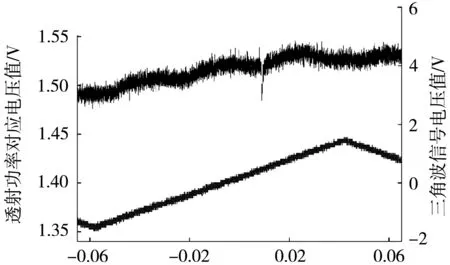
t/s

为了提升学生解决实际问题的能力,能够将实验现象观察与理论知识有机结合,学生在获得图3的实验数据后,利用数据处理软件(如Origin、Matlab)做进一步数据处理,以探明共振模式对应的谐振波长,与理论公式(1)相比较;进一步分析共振模式的线宽,深入理解系统损耗对共振产生的影响,这也是本实验教学的重要内容之一。

具体地,根据实验时设置的三角波信号参数和扫描激光中心频率,将图3中的横坐标时间转化激光波长,即一个上升沿的扫描时间0.1 s,对应激光扫描波长范围为0.248 nm;并对纵坐标电压值进行归一化处理,以透射功率的形式表示,数据处理结果如图4所示。

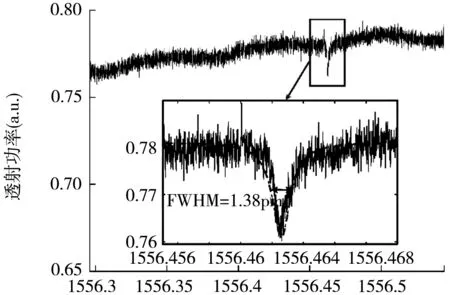
波长/nm

通过图4可以看出,当激光扫描波长为1 556.462 6 nm时,输出光功率在洛伦兹线型透射峰的最低点,表明此时激光频率与微球腔的本征频率发生共振,输出光功率达到最小。结合,令λ=1 556.462 6 nm,R=60 μm,neff=1.46带入公式(1),理论计算出该共振波长的角向量子数m为354。

作为实验教学的拓展部分,可以让同学们进一步计算该共振模式的半高全宽(Full Width Half Maximum,FWHM) ΔλFWHM=1.38 pm,通过查阅资料,计算出该共振模式的品质因子[12]Q=λ/ΔFWHM=1.13×106。从共振模式的测量结果分析,可以进一步看出,微球腔的品质因子越高,激光扫描频率靠近共振频率值时,越容易探测到激发出的共振模式。即从另一个角度可引导学生更深入理解为何产生共振现象的系统为欠阻尼振动(β<ω0)系统,当系统的品质因子越高,此时系统的能量耗散越小,所以外界振动频率越接近系统的本征频率时,才更容易发生共振,这与我们在《大学物理》课程中所学习的共振相关知识结论一致。

3 结 论

本文通过设计“基于回音壁微球腔的共振模式实验测量”教学实验,将科研课题与基础物理知识有机结合并融入教学中。探讨回音壁微球腔共振模式的实验测量方案,如何在实验中观察与记录共振模式,作为实验拓展教学环节,引导学生通过数据处理进一步加深对欠阻尼振动系统中共振现象的深入理解。该实验教学设计有助于拓展和丰富大学物理中共振现象的相关教学内容,同时也培养学生理论联系实际的能力、思考问题和解决问题的能力,夯实专业基础知识和专业技能,实现工程意识、科学创新能力的全方位培养。