离子推力器三栅极组件热形变仿真分析及试验研究

祁小峰，顾 左，代 鹏，李兴坤，李 贺

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

0 引言

离子推力器以离子产生、离子加速和离子中和3个主要工作过程的相对分离为内在特征，以应用栅极组件完成对放电室离子的分离、聚焦和加速引出为外在特征[1]。作为离子推力器的重要组成部分，栅极组件很大程度上决定了离子推力器的推力和比冲等性能，同时也是离子推力器寿命的重要影响因素。美国科研人员在对NSTAR离子推力器的长期研究中，认为离子推力器的在轨服务寿命和冷态启动时间主要由离子推力器的栅极组件所决定[2]。在离子推力器启动过程中，栅极组件的温度随时间逐渐升高，热形变位移也随之增大，直接影响离子的运动轨迹和栅极组件的导流系数，甚至导致栅极组件在亚导流系数或过导流系数状态下工作，增加了离子对栅极的轰击腐蚀。当栅极结构热形变严重，造成栅极间的非预期性击穿时，离子推力器的寿命就会受到影响。

美国在研制EB-GIT的初期最先注意到栅极热形变问题。1990年Mac等[3]利用等效弹性模量和泊松比建立了双栅极组件的有限元模型，并将实测形变量同仿真值进行对比，发现施加的温度场极大影响了栅极的热形变；2002年Shunk[4]针对球面结构的栅极提出材料参数的等效方法，并通过仿真计算得到栅极形变量。在试验方面，1989年Mac等[5]运用接触测量法测量了900系列和J系列在不引束流下的栅间距变化。对栅极形变的测量后来又出现了激光测距法，一种精度较高的非接触光学测量法，以及近些年来德国开发的多位一体测量法[6-11]，该方法能够同时测量温度、栅极曲率、栅极腐蚀、束流参数和等离子体参数。目前国外对栅极形变的研究已经比较成熟。国内孙明明等[12]采用有限元分析方法对20 cm、30 cm离子推力器三栅极组件进行了等效计算，模拟了热形变位移随工作时间的变化，预估了三栅极组件的冷态启动时间；梁秀强等[13]分别使用壳单元、体单元和梁单元建立了栅极组件有限元模型，计算并分析了栅极热形变与栅极开孔结构之间的关系。在实验方面，梁秀强等[14]基于实验室搭建的温度测量平台，测量了大气环境下加热时栅极组件的瞬态温度变化。目前国内通常采用人工热源加热或者在不引束流的条件下测量栅极的形变[15]。

本文以30 cm口径的三栅极组件为研究对象，对整个离子推力器建模，分析研究30 cm的栅极组件在2.3 kW功率下工作时栅间距的变化规律，并在真空环境中对该工况引束流条件下的栅间距随时间的变化进行在线测量，弥补国内试验方面的不足，验证仿真模型的正确性，为国内对30 cm三栅极组件的非预期性击穿、栅极溅射腐蚀和栅极形变等问题的研究提供参考。

1 仿真计算与试验测试方法

1.1 仿真计算方法

1.1.1 仿真模型的建立

为高效、精确地计算栅极热变形及热应力，利用PRO/E建立离子推力器的全尺寸有限元模型，将其导入有限元软件，并对其中的连接关系、相互接触面等进行细化，对复杂的内部结构进行布尔操作，以方便网格的划分以及计算结果的收敛。采用钼作为栅极材料，钼的溅射腐蚀率低，能够通过化学蚀刻形成多孔阵列，具有良好的热性能和结构性能，是离子推力器中最常使用的栅极材料。离子推力器的栅极组件为复杂的多孔、薄壁、带弧度的壳结构，无法直接进行有限元计算，为此将其等效为无孔、拱高不变的薄板结构，如图1所示。

图1 栅极模型图Fig.1 Original grid model and simplified model diagram

为了保证仿真结果的准确性，沿用孙明明等[16]对栅极材料弹性模量的等效结果，计算出栅极的等效弹性模量Eeff：

式中：E为弹性模量；l栅孔等效圆环外径；rc为栅孔等效圆环内径。

在此基础上，保持等效前后模型的质量和面积不变，利用开孔率对栅极材料的密度进行等效：

式中：ρeff为栅极材料的等效密度；ρ0为栅极材料实际密度；RA是栅极的开孔率；n为栅极开孔数量；rhole为栅孔半径；R为栅极口径。

1.1.2 边界条件

设计栅极组件时，为了尽可能地引出离子束流，同时最大限度地减少放电室内中性原子的损失，一般设计为屏栅极孔径最大，减速栅极次之，加速栅极孔径最小。之前的试验研究表明，由于加速栅极的阻挡，只有很少的离子轰击到减速栅极，减速栅极截获的电流很小，因此在设置边界条件时，主要对屏栅和加速栅施加热流量，忽略减速栅极的热流量。在引束流的情况下，直接测量栅极表面的温度分布难度很大，只能通过能量沉积模型进行仿真估算，然后运用热真空试验中测量得到的栅极组件边缘处的温度，对模型进行矫正，得到最终的屏栅和加速栅极的热流量。运用孙明明等[12]建立的环形会切磁场离子推力器热模型，计算得到30 cm离子推力器在2.3 kW下的能量沉积分布结果。屏栅和加速栅的热流量如图2所示，屏栅热流量为939.3 W/m2，加速栅极热流量为121.2 W/m2，屏栅靠近放电室，其热流量远远大于加速栅极。

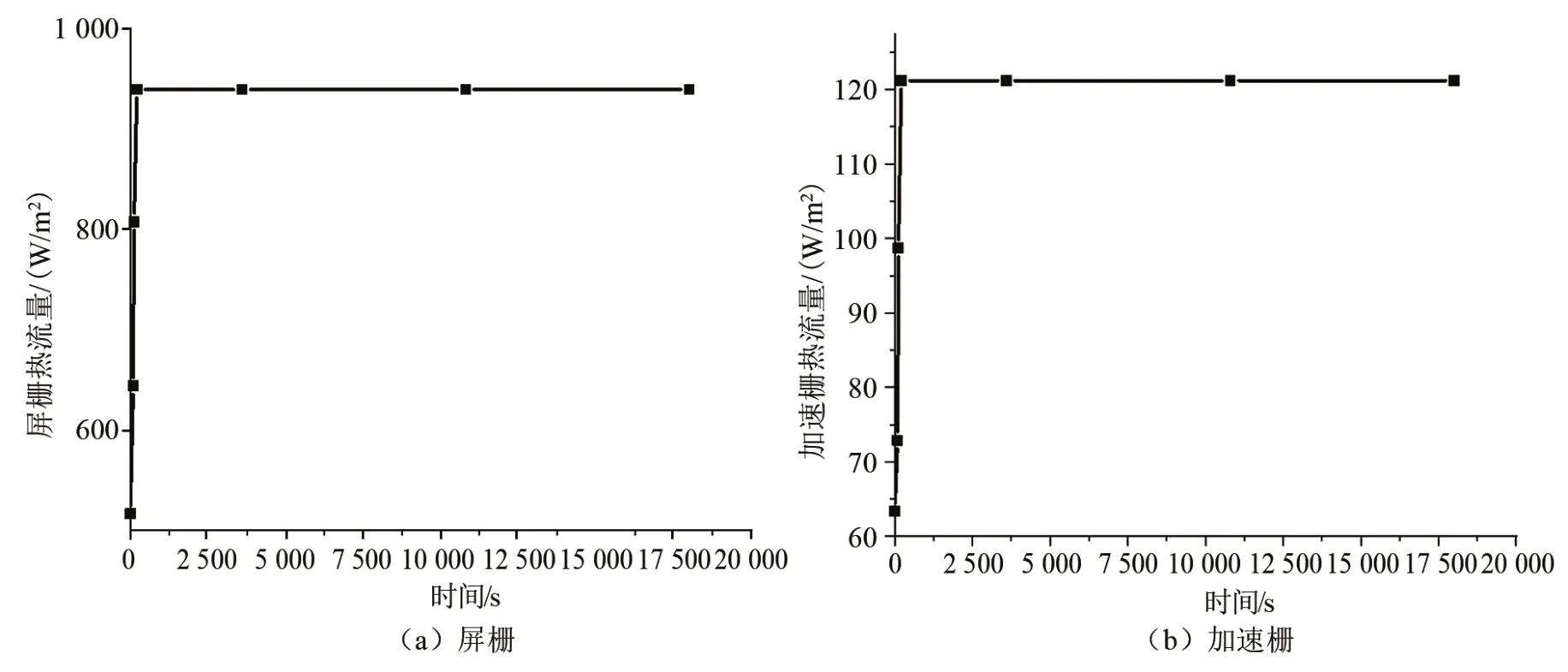
图2 栅极组件热流量输入曲线Fig.2 Heat flow input diagram of grid assembly

1.1.3 栅极温度分布

基于推力器仿真模型进行瞬态温度场仿真计算，屏栅极和加速栅极温度随时间变化趋势如图3所示。图中最大值和最小值分别表示离子推力器启动过程中栅极组件中心点和边缘处的温度值。栅极温度随时间逐渐升高，达到平衡时，屏栅极中心位置的温度为283.87℃，加速栅极为242.33℃，屏栅极边缘位置的温度为224.23℃，加速栅极为218.09℃。一般情况下，屏栅的设计厚度小于加速栅和减速栅的设计厚度，开孔率大于加速栅极的开孔率，因此屏栅极的热容远小于加速栅极。热容与温度的关系如式（4）所示，由图3可知，离子推力器启动过程中屏栅极的温度一直高于加速栅极，导致了离子推力器工作时屏栅-加速栅极栅间距的减小。

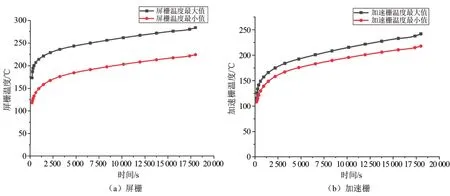
图3 不同时刻栅极组件温度最大值和最小值曲线Fig.3 Maximum temperature curve of grid assembly at different times

式中：C为热容；Q为热量；T为温度。

栅极组件达到热平衡时减速栅极的温度分布如图4所示，温度最高点在栅极的中心点，为222.39℃；温度从中心点向边缘逐渐降低，沿径向基本呈对称分布，同一半径的温度基本相同。屏栅和加速栅温度分布趋势与减速栅相似，这是由于栅极组件呈现凹面的特殊结构对离子束流有聚焦特性，导致引出离子束流的不均匀性。理论计算时，可以用一维热传导方程的基本解来预估，如式（5）所示。

图4 减速栅极温度分布图Fig.4 Temperature distribution diagram of deceleration grid

1.2 试验测试方法

1.2.1 试验测试系统

测试系统主要包括真空室、离子推力器、图像采集与处理系统、CCD相机、LED灯，如图5所示。测试试验在真空室内进行，真空室内极限压力≤5×10-5Pa，温度为0～40℃。真空泵运行时会产生一定的微振动，可能对测量结果造成误差。束流引出时陶瓷探针处于等离子体环境，束流半角约为15°。相机安装在离子推力器侧向约0.5 m处，用锡纸包裹，预防等离子体溅射。为保证光源的良好散热，用导热系数较高的不锈钢板材制作保护罩，通过导热硅脂与支架相连。陶瓷探针共两组，第一组位于栅极中心点，第二组位于中心偏下位置，以此来研究栅极形变沿径向的分布关系；每一组包含三个探针，分别用于标记屏栅极、加速栅极和减速栅极的位置，每个探针顶刻有十字标，有利于准确采集探针的位置坐标。

图5 栅极组件测试系统示意图Fig.5 Schematic diagram of grid assembly test system

1.2.2 试验步骤

测试流程如图6所示，将固定了陶瓷探针的栅极组件安装在离子推力器上，将CCD相机，LED灯等固定到真空室的指定位置，待通信正常后采集大气条件下探针位置图像，以此时探针的位置作为标定位置。完成采集后真空泵开始工作，当真空室内压力达到10-5Pa时，进行推力器放电室预处理、引束流，同时打开LED灯提供光源，用CCD相机采集图像，测试结束后将采集的图像通过图像处理系统运算后输出栅极位置的变化数据。

图6 栅极组件测试流程图Fig.6 Grid assembly test flow chart

1.2.3 精度验证

成像系统主要包括8 cm光学镜头、200万像素CCD相机、两台0～30 W补光用的LED灯（2维方向可调）和表面具有特征标识的陶瓷探针（十字特征及黑白对比度）。真空室关闭前，对测试系统进行标定，如图7所示：将一个标定板放置在探针同一平面内，通过对比图像中标定板上两点之间的距离和栅极上两点之间的距离来确定测量系统中的长度与实际长度的比例。抽气前，静止状态下探针位置变化测量结果如图8所示，可以看出，测量系统的精度在30 μm以内。

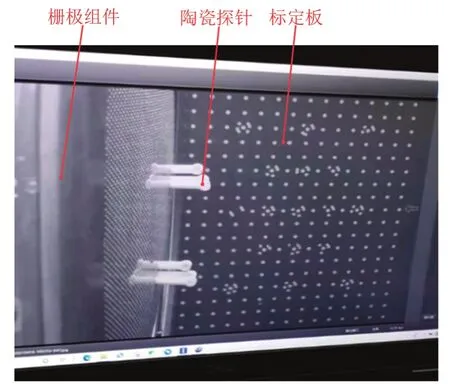
图7 图像采集系统中的探针图像Fig.7 Probe image in image acquisition system

图8 静止状态下探针测量精度验证曲线Fig.8 Probe measurement accuracy verification curve in static state

2 结果及讨论

2.1 仿真计算结果

2.1.1 栅极组件沿着径向坐标的热形变位移

以瞬态热仿真所得的温度分布结果作为输入条件进行热形变计算，研究在2.3 kW工况下栅极组件不同位置的形变量，绘制一条通过栅极中心的路径，1为起点，2为终点，如图9所示。从图中可以看出，栅极组件结构具有良好的对称性，通过栅极中心路径上的计算结果能够反映出同一时刻栅极不同位置的形变量。

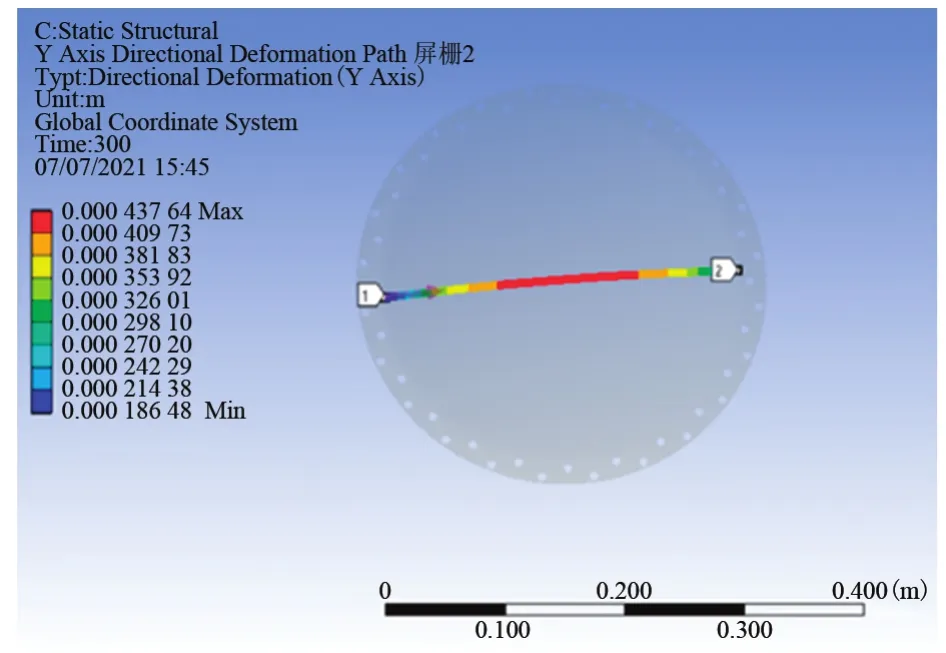
图9 栅极组件沿径向坐标热形变仿真图Fig.9 Simulation diagram of thermal deformation of grid assembly along radial coordinates

图10（a）（b）（c）为屏栅极、加速栅极和减速栅极在加入热量300 s后，在如图9所示距离起点1的水平位置的热形变位移。三个栅极的热形变趋势基本一致，均是中心位置形变量最大，屏栅极约为0.44 mm，加速栅极为0.26 mm，减速栅极为0.23 mm；边缘位置形变量最小，屏栅极约为0.19 mm，加速栅极为0.17 mm，减速栅极为0.13 mm。温度分布的不均匀性导致了栅极不同位置形变量的差异，可见，温度是造成栅极形变的最主要因素。虽然趋势一致，但形变量的大小存在差异，因为不同栅极所受热量不同，其中屏栅极开孔率最大，厚度最薄，因此热容量最小，形变量最大；减速栅厚度大于屏栅极，开孔率低，热容量大，且在离子推力器启动过程中减速栅温度低于屏栅温度与加速栅温度，因而形变量也最小，不同的形变量导致了栅间距的变化。

图10 栅极组件沿径向不同位置处的热形变Fig.10 Thermal deformation distribution curve of grid assembly along radial coordinates

从图10可以看出，栅极开始形变的时间也不尽相同，屏栅极最先变形，加速栅极次之，减速栅极最后变形，由此推测栅间距的最小值出现在离子推力器启动初期，且栅极中心处形变量最大，故为了校验栅极组件是否满足工作要求，取栅极组件中心处的点进行计算。

2.1.2 栅极组件中心点处的形变量

图11为离子推力器启动过程中，2.3 kW工况下栅极中心点的位移随时间的仿真结果。从图中可以看出，屏栅极、加速栅极和减速栅极中心点处的变化趋势相同，大约在1 800 s时，栅极形变量达到最大，屏栅极为0.452 mm，加速栅极为0.326 mm，减速栅极为0.235 mm，随后形变量基本维持稳定。为进一步研究热态栅间距的变化，用仿真结果的运算值绘制出栅间距的变化曲线，如图12所示。

图11 栅极组件中心点随时间的热形变曲线Fig.11 Thermal deformation curves of the center point of the grid assembly at different times

图12 栅极间距随时间变化曲线Fig.12 Variation of grid spacing with time during thruster start-up

从图12可以看出，屏栅-加速栅极间距减小量最大为0.28 mm，加速栅-减速栅极间距减小量最大为0.12 mm，栅间距变化的最大值均出现在离子推力器启动初期，随后略有减小，接着趋于稳定。一般情况下，冷态下的屏栅-加速栅极间距为0.9 mm，加速栅-减速栅极的栅间距为0.8 mm，因此在形变过程中，屏栅-加速栅极间距最小将变为0.62 mm，加速栅-减速栅极的栅间距最小将变为0.68 mm。之前的试验研究发现[16]，当30 mm离子推力器栅间距小于0.2 mm时，栅间打火现象频繁发生，因此将0.2 mm作为推力器正常启动的最小栅极间距要求，仿真结果表明该栅极组件的热形变在2.3 kW功率下满足工程应用要求。

2.2 试验测试结果

将采集到的图像通过图像处理系统与初始的标定图像进行比对计算，即得到栅极的形变量。中心探针和下端探针在2.3 kW时所测数据的点线图分别如图13、图14所示。推力器点火前，真空泵工作时产生的微小振动使探针的位置有轻微的前后波动，波动范围在±0.05 mm之内，后期计算栅间距时可相互抵消，对结果不会产生影响。屏栅极中心点的位移量大约为0.42 mm，加速栅极为0.27 mm，减速栅极为0.17 mm，下端探针测到的位移量略小于中心探针测到的，屏栅极下端探针测得的位移量为0.33 mm，加速栅极为0.22 mm，减速栅极为0.15 mm。

图13 中心探针测得的栅极组件形变量曲线Fig.13 Deformation of grid assembly measured by central probe

图14 下端探针测得的栅极组件形变量曲线Fig.14 Deformation of grid assembly measured by lower probe

离子推力器引束流时栅极组件中心点栅间距的变化量如图15所示，放电点火后，屏栅-加速栅极栅间距变化量最大值为-0.35 mm，稳定后减小为-0.15 mm，加速栅-减速栅极栅间距变化量最大值为-0.16 mm，稳定后减小为-0.10 mm。

图15 离子推力器启动过程中栅极组件中心点栅间距随时间变化量的试验结果Fig.15 Experimental value of grid spacing change with time during thruster start-up

2.3 仿真与试验对比分析

中心探针与下端探针测到的稳定后的热位移形变量对比如表1所列。可以看出，下端探针测得的热位移量（屏栅、加速栅和减速栅位移量）均小于中心探针测得的结果，这与栅极组件热位移沿径向坐标的仿真结果的变化趋势一致，栅极结构对离子束流的聚焦效果使得栅极中心处的温度最高，形变最大，因此在不考虑毛刺等的影响下，栅极中心成为最有可能发生非预期性击穿的位置。

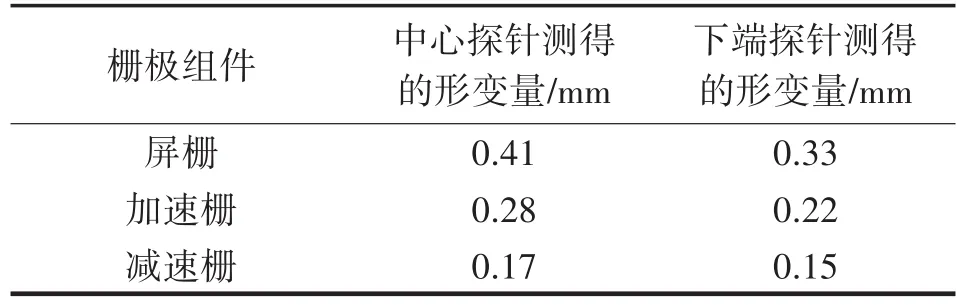
表1 中心探针与下端探针所测形变量结果对比Tab.1 Comparison of deformation measured by central probe and lower probe

在离子推力器启动过程中，栅间距变化量的试验结果与仿真结果对比如表2所列，屏栅-加速栅极、加速栅-减速栅极间距仿真结果都略小于实验值，这是由于对模型采取了一定的简化，通过对加速栅极和减速栅极施加热流来模拟离子推力器的启动过程，忽略了阳极筒热流、减速栅极热流和电压等次要影响因素，但仿真结果与试验结果的变化趋势完全一致。对比两者可以发现，离子推力器启动初期栅间距变化最快，也最容易出现非预期性击穿，原因是随着离子推力器启动放电，屏栅极的温度首先升高，由于栅极组件受到约束，因此受热后只能沿轴向膨胀，导致屏栅-加速栅极间距逐渐减小。随着离子束流的引出以及热辐射的影响，屏栅-加速栅极间距的形变量达到最大，随后加速栅极逐渐受热升温，开始沿着轴向膨胀，使得屏栅-加速栅极间距逐渐减小趋于稳定值；减速栅孔的孔径大于加速栅极，减速栅极的热量主要来自加速栅极辐射，温度变化较小，形变量也较小；加速栅极的膨胀导致加速栅-减速栅极的栅间距减小，但时间滞后于屏栅-加速栅极间距的变化。因此屏栅-加速栅极栅间距的大小是影响推力器的寿命和性能的关键参数。

表2 中心探针试验结果与仿真结果对比Tab.2 Comparison between simulation results and experimental results measured by central probe

3 结论

本文通过建模仿真与试验相结合，研究了离子推力器启动过程中栅极组件的热形变规律，通过对比分析，得到以下结论：

（1）仿真结果与试验结果一致性较好，表明利用该仿真模型研究模拟栅极组件热形变是适用的。

（2）同一时刻栅极组件沿着径向坐标热形变呈对称分布，中心位置形变量最大，向边缘逐渐减小，加速-减速栅极栅间距变化量远小于屏栅-加速栅极栅间距变化量，因此加速栅-减速栅极冷态栅间距是栅极组件设计的关键。

（3）离子推力器启动时，由于屏栅极最先开始热膨胀，导致该时刻屏栅-加速栅极栅间距迅速缩小，在栅极组件中心处，屏栅-加速栅极栅间距变化量迅速达到最大值0.35 mm，之后随着加速栅极的受热膨胀，屏栅-加速栅的栅间距变化量逐渐趋于稳定值0.15 mm。