液氧罐晃动时防波板对罐体受力的影响
张瀚月,陈建业,李 军,李雁飞,谢军龙
(1.华中科技大学 能源与动力工程学院,武汉 430074;2.海军工程大学 动力工程学院,武汉 430033)
0 引言
晃动是一种复杂的流体运动现象,其晃动形态和类型多种多样,如平面晃动、非平面晃动、旋转运动和准周期运动等。由于自由液面的存在,液体晃动具有很强的随机性和非线性,若容器运动较为剧烈,罐内液体还会产生液体破碎、运动混沌的现象[1]。船舶在海上航行,液氧罐一直处在运动状态,罐内液氧晃动而不断冲击罐内壁,产生局部冲击载荷。对于船用LNG,如果罐内充装度不足,船舶运动会诱发罐内LNG的晃荡。在一定频率的冲击作用下,罐体结构会受到较强的损害,使用寿命缩短。因此,有必要分析液氧罐中的液体晃动,了解晃动过程,并对液氧罐进行受力分析。研究液氧罐所受冲击力的变化规律有助于了解液体晃动对液氧罐破坏的强度和规律,从而改进罐体结构与材料,设置合理的防晃装置等。
数值模拟方法广泛应用于液体晃动问题。晃动仿真从单纯模拟介质晃动过程开始发展,之后增加了防晃措施的研究,其中研究罐和防波板受力是很重要的一部分。刘雪梅[2]研究了等效质量法、平均压力法和冲击载荷法的惯性力加载方式,比较了三种方式对设备强度的影响,讨论了不同参数对液体晃动的影响。孙丽娜等[3]使用VOF模型研究罐车液体充装率、密度和黏度对罐体水击压力的影响。田晋跃等[4]利用仿真分析了不同充液比下罐车在三个坐标方向上的受力情况。肖武等[5]采用MPS方法,以罐体上几点受力变化为指标,探究LNG液舱不同激励形式下装载高度和激励频率的影响,发现激励频率在固有频率附近时受力最大。提高晃动模拟的精确性是晃动研究的主要目标。陈海阳等[6]采用VOF模型模拟二维SPB型LNG液舱内储液的晃动特性,发现晃动随着充液率的增大和运输船初速度的减小而减弱。祁江涛等[7]结合动网格与VOF模型,建立了适合不同形状的液舱晃动数值模拟的计算方法。臧垒垒等[8]基于VOF模型研究晃荡周期对液舱受力与内部波性的影响,优化了液舱型式,得到了双列结构的液舱,有效地降低了晃荡的冲击影响。Liu等[9-11]使用VOF模型和动网格技术相结合来优化模拟,监测晃动力、晃动力矩的变化和自由表面动态响应特性,探究液位影响,为非规则激励下流体晃动的抑制提供了有效建议。Hu等[12]采用RANS求解器模拟晃动,运用UMTHINC网格格式结合湍流模型处理自由表面,保证自由表面的清晰界面,并分析了不同晃动频率下多种湍流模型在仿真晃动中的区别。
在防晃措施的研究中,大量研究表明防波板是抑制晃动最有效的方式之一。陈志伟[13]确立罐车减速时的等效力学模型后,使用VOF方法研究不同制动加速度和充液比下封头受力变化规律,并分析防波板的防晃效果。刘奎等[14]采用VOF模型研究不同充液率下防波板面积对罐体受力的影响。Brar等[15]利用COMSOL仿真液氧罐晃动,研究防波板的组合方式对罐体受压的影响,发现水平和垂直防波板的组合方式最有效。刘东进等[16]使用ABAQUS模拟LNG储罐晃动,发现锥形防波板的防晃效果最佳。Patnaik等[17]使用OpenFOAM模拟晃动动力,研究谐振谐波激励对罐体压力分布和晃荡力的影响,并优化了垂直挡板的尺寸。王琼瑶等[18]使用VOF方法研究防波板的设计参数对纵向力载荷转移量的影响,分析空气压力抑制液体晃动的影响机制。Akyildiz[19]模拟T型防波板的防晃过程,研究防波板的拓扑结构、自由表面变形和涡度分布,发现此类防波板对晃荡有良好的抑制作用,并且当T型挡板高度大于液面高度80%时,防波板对矩形储罐的晃荡抑制完全有效。
若不将防波板视为刚性体,液体晃动实际上是流固耦合问题,因此需关注罐内液体与防波板间的耦合以提高模拟精度。Hwang等[20]使用组合粒子的形式改善MPS方法,并采取精确的区域扫描自由表面搜索方法评估自由表面,利用FSI模拟了弹性板对晃动的抑制作用和效果,探究不同弹性模量的挡板对罐体受压的影响。刘小民等[21]采用双向耦合的方法模拟液氧罐在制动状态下的晃动,研究了不同材料的防波板变形和受力情况以及罐体的整体受力情况。
本文主要研究船舶上液氧罐的晃动问题,设置的晃动振幅大于液体深度的1%,属于大幅度的晃动问题[13]。此类问题无法线性简化,且自由液面边界条件是非线性方程[22]。如今,数值模拟法已能有效直观地模拟大幅晃动现象并揭示液氧罐的受力规律,能自主设置外在条件且全面考虑各种影响因素,适用范围较广,可更简便地调整晃动条件参数,从而快速设置不同工况,研究各类参数对罐体受力情况的影响。仿真模型将罐体和防波板设置为刚体,忽略固体结构和液体间的耦合作用。基于上述前提条件,对液氧罐晃动所受的冲击作用进行分析。
分析过程采用数值模拟研究横摇状态下罐壁面的冲击特性,分析液氧罐受到冲击作用的机理,再基于罐内液体的流动特性,分析计算内壁受到的压力和晃动力随时间的变化规律。探究加入T型防波板[23]后液氧罐受到的压力和定向晃动力随时间的变化规律,并与未加防波板方案进行对比,同时初步分析和对比两种防波板的受力情况,提出防晃建议。
1 液氧罐计算模型
1.1 液氧罐几何模型参数
本文液氧罐几何模型如图1所示。罐全长L=1 900 mm,两端为标准圆形封头,罐直径D=860 mm。后期计划搭建液氧罐晃动试验台,液氧罐尺寸同上,体积约1 m3。对比研究两种不同高度的T型防波板,忽略厚度的影响,水平板宽430 mm,竖直高度分别取0.5D和0.75D以对比研究高度的影响。在X方向施加正弦激励使液氧罐晃动。

图1 全尺寸液氧罐模型Fig.1 Model of full-size liquid oxygen tank
1.2 数值模型
在模拟之前,引入假设条件:(1)将液氧视为不可压缩流体;(2)将氧气视为理想气体;(3)罐体为刚性容器,壁面无滑移且不考虑和液氧的耦合作用。
采用欧拉多相流模型对气液两相分别求解。液氧罐晃动时分散相集中在液体自由表面附近,分散相和连续相被视为连续的一体,相间阻力由代数界面面积密度模型求得,计算精度更高。气液相分别设为液氧和氧气,定义液相为主相,氧气为次相,开启两相间的气液传质模型。针对该问题进行非稳态计算,选择双精度和压力求解器进行求解。考虑低雷诺数和剪切流传播,湍流模型选取标准k-Omega模型。求解方法为SIMPLE方法,用一阶迎风格式分别求解时均N-S方程、连续性方程以及湍流附加方程,压力离散采用Body Force Weighted格式。边界条件设为无滑移壁面边界。设置时间步长为10-5s,残差收敛标准为10-4。罐内初始压力为表压130 kPa,重力加速度g=-9.8 m/s2。边界条件设为壁面无滑移边界条件。晃动通过自主编制的UDF实现,在X轴方向加载正弦晃动激励于液相上,振幅为0.2 m,频率为1.0 Hz。当液氧罐的充液率过高或过低,液体晃动对储罐的冲击力较小,为了验证液氧罐防波板设置的有效性,设置液氧罐的充液比为0.5。
2 模型有效性检验
2.1 网格无关性验证
使用无挡板的液氧罐模型进行网格无关性验证,选择129 630、289 942、597 590和861 868四种网格来分别计算。在施加正弦激励的情况下,计算罐壁受到的横向晃动力。使用不同网格计算出的晃动力如图2所示。可以发现,当网格增加到289 942时,计算出的横向晃动力随着网格数增加几乎不变。因此,在减少计算资源和提高计算精度的基础上,选择289 942网格的进行模型计算。在此基础上,再设置了添加T型防波板(高度为0.5D和0.75D)的液氧罐模型,网格数分别为296 136和322 179。图3为设置防波板(H=0.5D)后的液氧罐网格模型。

图2 网格数对晃动力的模拟值的影响曲线Fig.2 The effect of grid number on the sloshing force

图3 设置H=0.5D防波板的液氧罐模型Fig.3 The liquid oxygen tank model with H=0.5D baffle
2.2 模型验证
采用Xue等[24]的晃动实验数据验证数值模型。该实验研究了在较宽的激励频率下,四种类型的防波板设置方案对液体冲击液氧罐的抑制效果。选取其中两个实验数据验证数值模型,图4(a)和图4(b)分别为实验一和实验二的罐壁所受压力波动快速傅里叶变换(FFT)分析的实验值与模拟值对比图。可以发现,数值模拟得到的主要频率和对应振幅与实验值吻合较好,验证了数值模型的准确性。

图4 罐壁所受压力波动的频幅特性对比Fig.4 Frequency and amplitude characteristic curve of pressure fluctuation on tank wall
3 结果与分析
3.1 晃动过程罐内两相流动特性
液氧罐的正弦运动规律为0~0.25 s罐体逆时针加速转动,t=0.25 s后减速转动,t=0.5 s液氧罐转动方向改变,且以t=0.75 s为节点转动速率先增大后减小。随着正弦波的传播,气液界面会出现较大的扰动和界面波动。0~0.5 s可被看作晃动的第一阶段,液氧初始状态为静止,先向左侧涌动,液面波动不大。t=0.5 s罐体运动转向,晃动进入第二阶段,0.5~1.0 s可看作第二阶段,液体在惯性的作用下仍然向罐左侧流动,第二阶段的初始状态为向左侧流动,液体运动相对于罐体具有滞后性。t=0.6 s,一部分液体随着罐转动方向的改变而向右侧流动,一部分由于惯性而依然向左侧流动,罐两侧的液体向罐中心流动发生碰撞,导致碎波产生。其中0.6~0.7 s罐内碎波程度最大。t=0.8 s液体运动已趋于稳定,流动方向也基本一致,统一向罐右侧流动。t=1.0 s罐体逆时针转动的角度达到了最大值,液体向右侧涌动的幅度也达到了最大值。由于在0.5~0.8 s期间液体的晃动最为显著,所以重点关注该时段内设置两种防波板后的液氧罐晃动相图,图5为该时间段内选取4个时刻的晃动过程罐内流态变化图。肖武等[5]在船运LNG的两相仿真中也发现了类似规律。
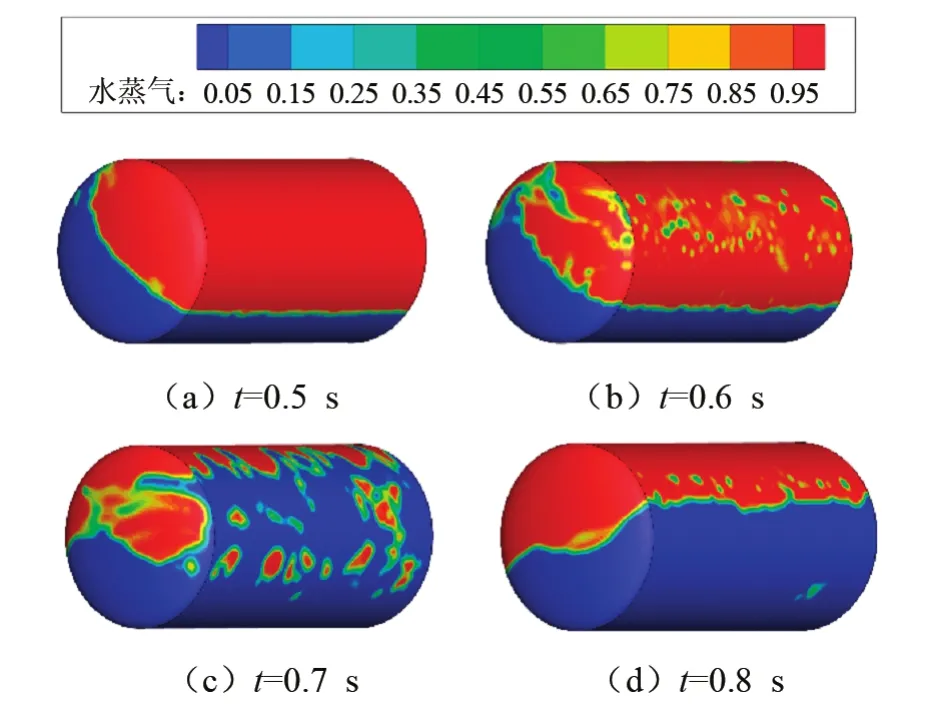
图5 无防波板情况下的晃动相图(0.50~0.80 s)Fig.5 Sloshing phase diagram without baffle with in 0.50~0.80 s
图6和图7分别为设置了高度0.5D和0.75D防波板的罐内晃动流态图,发现设置了防波板后相界面波动明显减少,可见防波板对晃动具有较为显著的抑制作用。对比发现设置了H=0.5D的防波板后碎波相对更少。

图6 设置H=0.5D防波板情况下的晃动相图(0.50~0.80 s)Fig.6 Sloshing phase diagram at 0.50~0.80 s with H=0.5D baffle
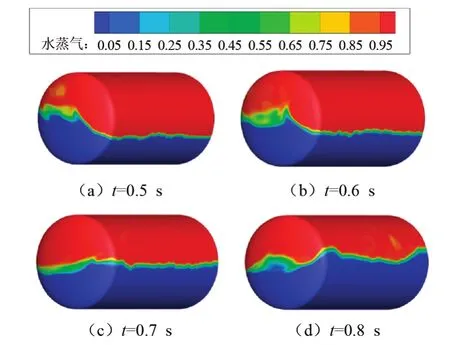
图7 设置H=0.75D防波板情况下的晃动相图(0.50~0.80 s)Fig.7 Sloshing phase diagram at 0.50~0.80 s with H=0.75D baffle
3.2 液氧罐压力波动特性
3.2.1 罐壁的压力变化规律
图8对比了无防波板和添加不同高度防波板的罐壁面所受平均压力。可以看到防波板的设置大幅减小了压力波动幅度,使罐壁受压更平均,降低了冲击负荷。且设置防波板的压力波动的频率更大,若将压力波动的曲线近似看作一种周期变化曲线,未设置防波板时压力波动周期为0.6 s,设置高度为0.5D和0.75D的防波板后周期分别减小到0.5 s和0.3 s。随着防波板高度的增加,压力随时间变化的规律性减弱且波动程度大幅度减小。
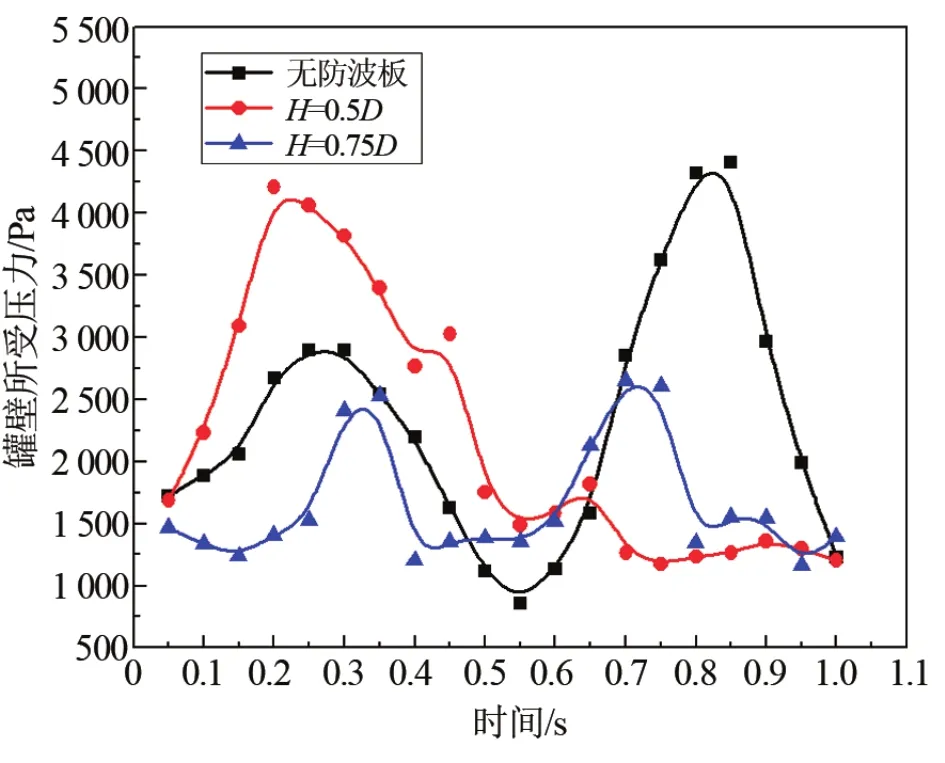
图8 三种方案下罐壁平均压力随时间的变化曲线Fig.8 Curve of average pressure intensity on tank wall with time in three cases
未设置防波板时,液氧罐的转动速率在t=0.25 s最大,液体冲击强度较大,在惯性作用下,液体运动滞后于罐体运动约0.05 s,即在t=0.3 s压力极大,但过后罐体转动速率减慢。进入第二阶段,液氧罐所受冲击程度减缓至t=0.55 s时罐体受压最小,在罐体转动方向改变时液体的运动方向完全与之相反,液体需要适应并跟随罐体运动所需时间相较第一阶段更长,液体运动滞后于罐体运动约0.1 s。压力在t=0.85 s最大,之后罐体受压随着罐体转动速率的减慢而减小,液体的运动状态逐渐趋于稳定。
设置0.5D高度的防波板后罐体受压同样先增大后减小,随后以相同的变化规律不断波动且波动程度逐渐减小。图9发现罐体此时的平均受压和最大压力差变小,防波板大幅减小了第二阶段的罐壁压力波动,也对整个周期的液体冲击都起到了轻微抑制作用,但罐壁压力变化的规律性相对减弱。

图9 罐壁受压相对无防波板倍数曲线Fig.9 Diagram of side wall pressure multiples compared to the case without baffle
t=0.2 s压力达到最大值,因为防波板的高度与液面高度一致,在晃动的第一阶段,T型防波板的水平挡板大幅缩小了自由液面处液体活动的空间,减小了其运动幅度,降低了液体内部对冲击的缓冲作用。所以在初期,冲击变化幅度最大,而液体的波动会逐渐适应防波板的阻碍作用,波动幅度减弱。设置高度为0.75D的防波板后压力波动几乎无规律,由图9得知,罐壁所受平均压力最小且最大差值远远小于前两种情况。此时自由液面处液体的运动空间大小介于前两者之间,轻微降低了对冲击的缓冲作用,所以在第一阶段罐体所受冲击作用较大但不是最大。在0.5~0.75 s内,罐体与液体的运动方向由完全相反转变为一致,液体运动状态的改变程度最大,因此液氧罐受压的最大值出现在晃动的第二阶段。
3.2.2 封头的压力变化规律
图10为三种方案下的后封头受压规律对比图,前后封头所受到的压力大小和变化规律基本相同。未设置防波板时封头受压变化的规律性最强,随着防波板高度的增加,压力变化的规律性减弱,且防波板增加了封头受压频率。设置H=0.75D防波板后封头所受压力的波动程度最小。其他变化规律与罐壁受压的变化情况相同。
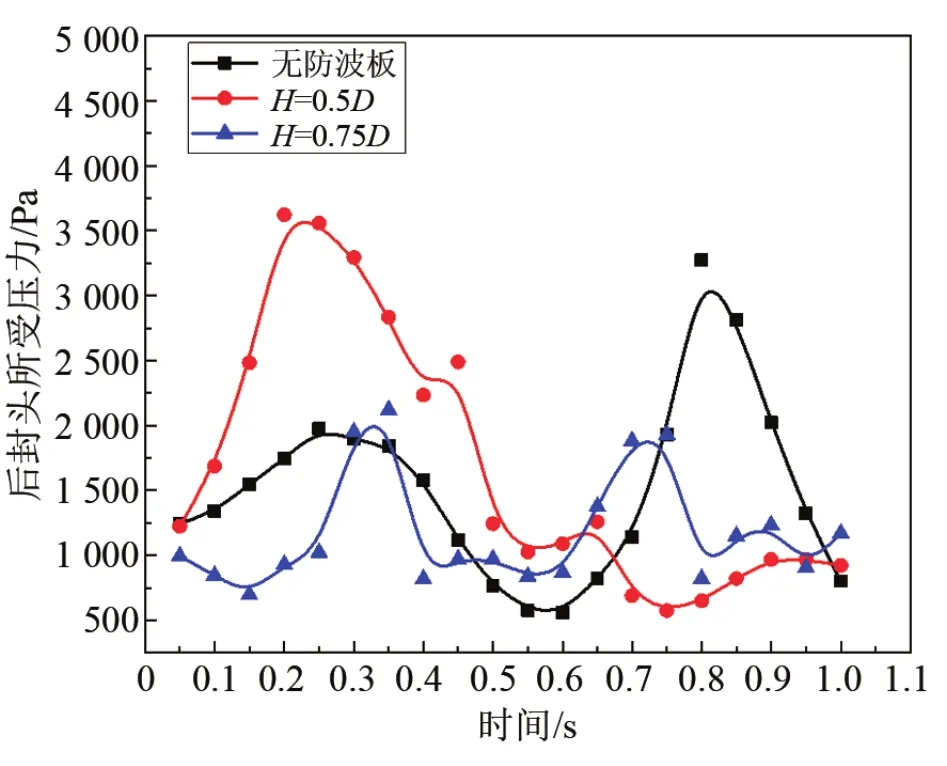
图10 三种方案下后封头平均压力随时间的变化曲线Fig.10 Curve of average pressure intensity of rear head with time in three cases
由图11可得H=0.5D防波板会增大受压程度,由于此时防波板与液面高度一致,T型水平防波板将液体沿X轴方向上的运动分散到沿Z轴方向上的运动,即垂直于前后封头运动。设置高度为0.75D防波板时罐壁和封头平均受压和压力波动程度最小。虽然此时的封头受到的均压相较设置高度为0.5D的防波板时相差不大,但与罐壁受压相对比,罐壁平均受压近似为封头的两倍,罐壁受力是液氧罐受力的主要来源。综上,高度为0.75D防波板对液体晃动的抑制程度更显著。除此之外,设置0.75D高度的防波板会同时减小罐壁和前后封头所受到的液体冲击压力,且两者所受平均压力差别更小,罐体受压更为均匀。

图11 后封头受压相对无防波板倍数曲线Fig.11 Diagram of rear head pressure multiples compared to the case without baffle
3.3 液氧罐晃动力对比分析
3.3.1 罐壁受力分析
虽然液体晃动对罐体所产生的动反力主要由液体腔壁边界上的液体压力来反映[25],但为了清晰地了解罐体所受液体晃动冲击的主要方向来源,研究罐体在不同方向上所受晃动力的变化特性也是十分必要的,从而更有针对性地保护罐体。罐体在X轴方向的受力为横向受力,在Y轴方向的受力为纵向受力。
图12为三种方案下罐壁受横向晃动力变化图,可以看出罐壁的横向受力变化规律与受压类似,设置防波板对受力变化的频率没有影响,而且三种方案的受力变化规律一致,与正弦激励规律基本相同。随着罐体转动速率的变化,冲击力逐渐增大后再减小并反向,但液体运动滞后于罐体,所以极值出现及反向时刻推迟0.05~0.15 s。随着防波板高度的增加,两个阶段罐壁受力大小更为接近,以竖直防波板为对称面的左右横向受力对称程度增加,即罐壁受力更加均匀。
当液氧罐未设置防波板时,由于液体的惯性作用,冲击力极值出现时刻有所推迟。两个极值分别先后产生于晃动的第一阶段和第二阶段,第一阶段的液体初始状态为静止,第二阶段初始状态为向左流动,且此时液氧罐改变转动方向,带动液体反向流动,所以相对于第一个极值,第二个极值产生时液体晃动幅度更大。因此第二个冲击力极值较第一次更大,达到最大值。两次极值的不同主要是因为在相应半个周期内,液氧罐的初始状态不同。由图12和图14可以发现两种高度的防波板都能有效抑制液体晃动,减小液体对罐壁的冲击作用。并且H=0.75D的防波板能极大减小罐壁的受力负荷,抑制晃动的效果更明显。
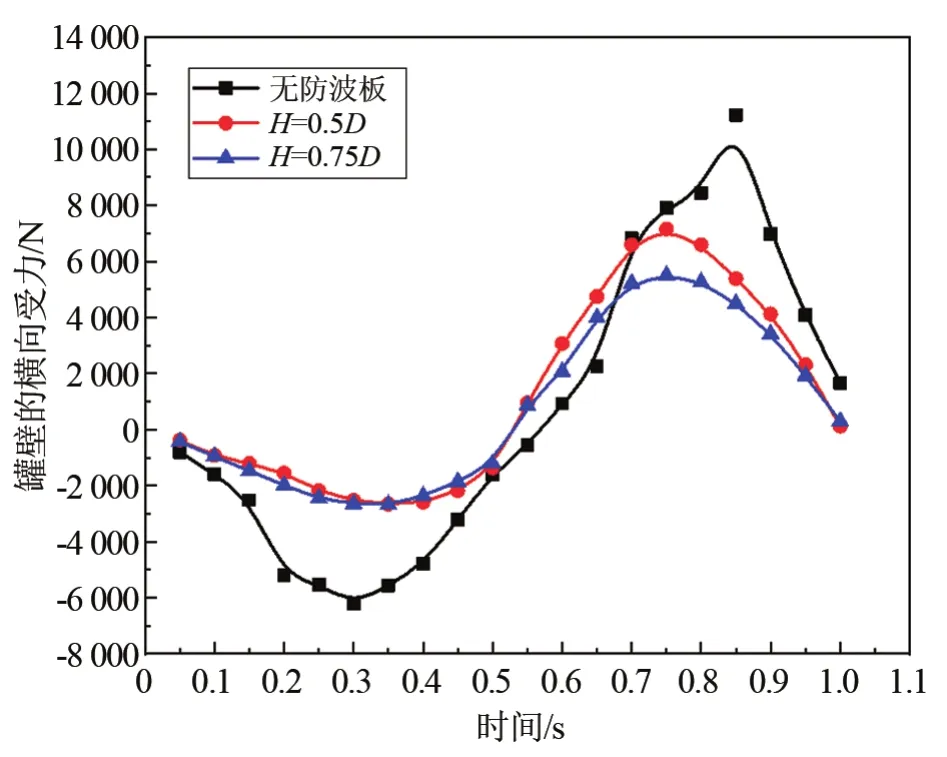
图12 三种方案下罐壁横向受力随时间变化曲线Fig.12 Curve of lateral force on tank wall changing with time in three cases
由图13和图14可知,设置防波板后罐壁的纵向平均受力变小,未设置防波板时罐壁的纵向受力规律性较弱,先降低再上升,再经过大幅度降低后回升。
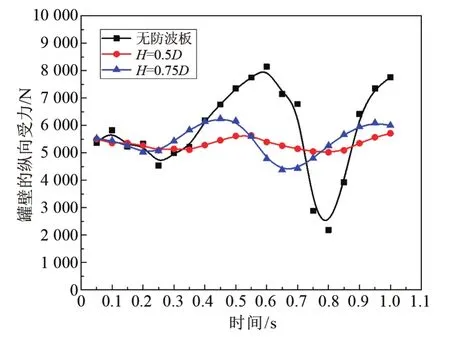
图13 三种方案下罐壁纵向受力随时间变化曲线Fig.13 Curve of longitudinal force on tank wall with time in three cases

图14 罐壁受力相对无防波板倍数图Fig.14 Diagram of wall force multiples compared to the case without baffle
在t=0.8 s时液体经过了最剧烈地晃动,大部分液体处于碎波形态,液体施加给罐壁的冲击作用分散,晃动力大幅减弱。设置防波板后纵向受力变化的规律性增强,波动幅度降低,且随着防波板高度的增加,波动周期变短。这说明水平防波板阻碍自由液面处液体的纵向运动,缩小液体自由活动的空间,从而降低液体晃动程度。
3.3.2 封头受力分析
基于横摇的晃动方式,前后封头所受到的晃动力基本都源于Z轴方向,所以晃动力变化曲线与封头受压曲线的规律基本一致,且两种防晃方案相对于未设置防波板方案的晃动力大小的相对比例与封头受压的相对比例基本相同。即设置H=0.75D的防波板能同时减小封头和罐壁受力的均值和最大差值,减小罐体各面间的受力差。
3.4 不同高度防波板受力对比分析
由图15和图16可知,H=0.5D防波板所受的压力分布更均匀,因为此时防波板的高度和初始液面高度一致,防波板所受压力主要源于液体晃动冲击。而H=0.75D防波板则存在较大的压力梯度,由于该防波板一部分在液相中,一部分在气相中,在气相中的防波板部分所受压力更大。且在自由液面的高度处出现较大的压力梯度,导致应力集中,需重点关注防波板中位于自由液面处的部分,对该部分的应力变化进行监测。
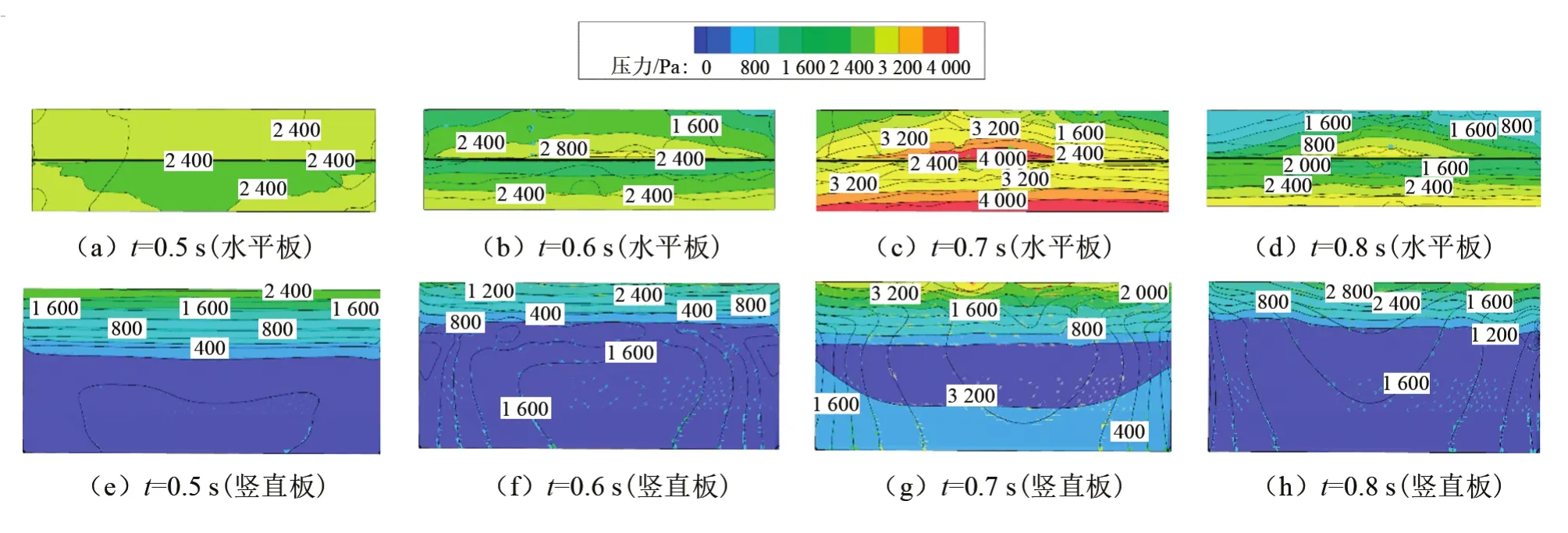
图15 高度为0.75D防波板的压力云图Fig.15 Pressure diagram of H=0.75D baffle
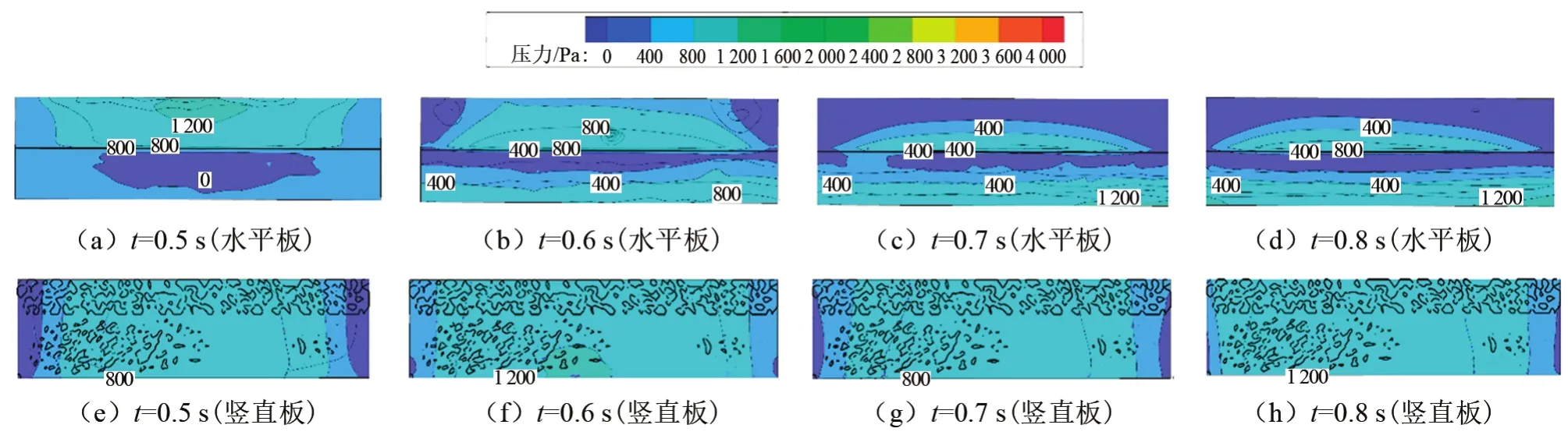
图16 高度为0.5D防波板的压力云图Fig.16 Pressure diagram of H=0.5D baffle
防波板自身所受到的液体冲击不容忽略,在防波板的使用期限内,需要时刻对防波板的结构强度进行检测并对防波板进行修理和加固,才能持续地抑制液体晃动,最终保护液氧罐。图17和图18展现了不同高度防波板在同一充液比下的受力规律,可得到H=0.75D竖直防波板所受的冲击变化幅度更大的结论。防波板越高,受压面更大,并且0.75D的防波板处于气液两相之中,气液两相压力差较大,增加了受力波动幅度。0.75D防波板的水平部分所受冲击力也相对更大,这是由于0.5D的水平防波板主要处于气液两相中,而0.75D的水平防波板全部处于纯气相中,由于液体对压力的传播具有缓冲作用,气体扰动施加给防波板的压力远大于液体晃动施加的压力[18]。同时考虑0.5D的水平防波板处于两相交界处,它受自由液面的冲击导致波动较为剧烈。综合分析,高度为0.75D的防波板受力更大,更易损坏。

图17 T型防波板竖直板受力随时间变化曲线Fig.17 Curve of force on vertical baffle changing with time

图18 T型防波板水平板受力随时间变化曲线Fig.18 Curve of force on horizontal baffle changing with time
4 结论
本文针对横摇状态下的液氧罐晃动开展研究,建立了液氧罐三维数值模型,着重分析了在充液比为0.5下安装不同高度防波板时液氧罐罐壁、封头和防波板所受压力和定向晃动力的变化情况,得出以下结论:
(1)晃动过程中罐内流动特性:设置H=0.75D防波板后罐壁平均受压和压力变化程度最小,罐壁受压是液氧罐受压的主要来源,且此时封头受压同样大幅减小,全罐受压更为均匀,所以高度为0.75D的防波板对液体晃动的抑制程度更显著。
(2)罐壁受力:设置H=0.75D的防波板能更好地抑制液体晃动。设置H=0.75D的防波板后罐壁横向受力的均值和最大差值在三种方案中最小,分别减小到不设置防波板时的0.58倍和0.49倍,且减小了罐壁的纵向受力,减小了罐壁的受力负荷。设置H=0.75D的防波板后以竖直防波板为对称面的罐体侧壁的左右两侧受力大小相差不大,受力较为均匀。同时,封头受冲击的情况也有较大的改善,受力减小,全罐的受力更为平均,有利于增加液氧罐的使用寿命。
(3)防波板受力:在液氧罐充液比为0.5的情况下,H=0.75D的防波板所受的冲击载荷大于H=0.5D的防波板。位于自由液面高度的防波板部分,会出现较大的压力梯度,这会导致应力集中,所以需重点关注防波板位于自由液面处的部分,应随时监测该部分的应力变化。
致谢
本文的计算工作得到了华中科技大学网络与计算中心提供的公共计算服务平台支持,在此向各位老师表示衷心的感谢!

