基于硅基回热器的微型脉管制冷机的数值模拟
王浩任,王 博,李睿泽,巢翊钧,尹传林 ,赵钦宇,甘智华,
(1.浙江大学 浙江省制冷与低温技术重点实验室,杭州 310027;2.浙大城市学院低温中心,杭州 310015;3.低温技术安徽省重点实验室,合肥 230088)
0 引言
近年来,随着电子器件的集成化、微型化程度的不断提高,其热流密度进一步增加[1],使得电子器件的散热问题成为制约电子器件正常工作和性能进一步提升的关键,对微结构的高效散热提出了迫切需求。当前数据服务器电子器件的主要冷却方式为风冷和液冷两种方式[2],通过换热器或者热管使用直接或间接冷却的手段对全部件(包括芯片及外围器件)进行冷却。上述冷却方式中,风冷的方式由于空气较差的热物性导致其传热极限小,而液冷的方式则存在可能引起泄露污染以及维护成本高等不足,使得风冷和液冷方式无法完全满足当前微电子器件高效散热的要求。
针对电子器件的高效冷却需求,研究人员尝试了许多新型的制冷结构,其中较为广泛应用的主要有热电制冷技术[3]、微型芯片节流制冷技术[4-7]和微型斯特林制冷技术[8-9]等。由于热电材料的优值系数(ZT)值较低,目前热电制冷机的效率也较低。微型节流制冷机利用工质的节流制冷效应进行冷却,存在降温速率慢、易冰堵等问题。
近年来,采用微纳加工方法的微型斯特林制冷系统因其具有结构紧凑、制冷温区宽等优点而成为研究的热点。一方面由于微纳加工技术有利于实现微结构中点对点的高效冷却方式;另一方面则是斯特林制冷技术的制冷温区宽,无工作温区的限制,且可实现在低温温区(<120 K)的高效制冷。基于微型主动制冷系统的潜在优势,美国国防部高级研究计划局(DARPA)就电子器件冷却制定了专门的研究计划[10],要求制冷系统的性能系数(COP)不小于2,该计划有力地促进了微型主动制冷系统的研究。
在微型斯特林制冷机方面,美国国家航天局(National Aeronautics and Space Administration,NASA)的格林研究中心(Glenn Research Center,GRC)在2001-2006年研制了运行频率为1 000 Hz、整机长度为220 mm的微型平面斯特林制冷机[11-12],其回热器材料采用不锈钢纤维,无负载运行获得了20 K的冷热端温差,相对卡诺效率达30%,然而,由于回热器冷热端温度测试的精度不足,难以为后续微型斯特林制冷机提供设计支撑。
卡耐基梅隆大学(Carnegie Mellon University,CMU)的Guo等[13-14]在2011年提出一种新型的微型斯特林制冷机(Stirling Cycle Micro-refrigeration System,SCMS)。SCMS由硅晶片加工而成,内部充气压力为0.2 MPa、整机长5 mm、宽2.5 mm、回热器部分长0.5 mm。计算结果表明,该微型制冷机运行频率为2 000 Hz,单个元件能达到冷热端25 K的温差,一般使用时为多元件叠加工作。国内华中科技大学的Liu[15]和Song等[16]对微型斯特林制冷机的循环过程进行了数值模拟,该模拟基于的制冷机长度为6 mm,最终冷热端实现了12 K的冷热端温差。
采用硅基回热器的微型脉管制冷机,充分利用了微纳加工的紧凑性和冷端无运动部件、振动小等特点,可进一步提升整机的可靠性。对于方形回热器,目前的膜片材质较为合适的工作频率为500 Hz[11]。同时本文根据NASA和Guo等的设计尺寸,结合现有的生产条件,最终确定了方形硅基回热器的尺寸:长度30 mm,截面为10 mm×10 mm。由于微型部件不耐压,因此设计的平均充注压力为0.2 MPa。本文使用Fluent 19.0软件,研究冷热端温度、空隙率及相位等参数对基于硅基回热器的微型脉管制冷机的影响,为微型脉管制冷机制冷性能的优化提供理论计算支撑。
1 微型脉管制冷机的建模
1.1 几何模型的构建与简化
本文研究的微型脉管制冷机的回热器为长30 mm,宽10 mm,高10 mm的长方体,如图1所示。图中回热器部分的材料为硅,冷端换热器(CHX)和热端换热器(HHX)为铜制的狭缝式换热器,调相结构采用惯性管和气库进行调相。整机结构尺寸较小,因此在截面处可近似认为其质量流和压力波的分布是均匀的。Fluent软件中建立脉管制冷机数值模型,为定量分析制冷机内部的相关机理提供理论基础,在与实验结果对比上具有较大的可靠性[17]。因此文中模型的建立与部分参数的设置参考了文献[17]中的相关内容。在计算中,级后冷却器左侧边界设置为压力入口,将热端换热器右侧边界设为质量流出口。由于调相机构的具体尺寸需要通过制冷性能进一步确定,而调相机构的效果可以通过调节质量流出口与压力波入口的相位来体现,因此本文模型不对调相机构进行具体建模。图1所示的制冷机结构具有对称性,因此通过取中心截面的方式将模拟计算简化为二维平面。为便于探究微型回热器内部机理,对整机先使用Gambit软件进行网格划分,相关的计算域以及边界的命名如图2所示。

图1 微型脉管制冷机部件示意图Fig.1 Schematic of the micro-pulse tube refrigerator

图2 微型脉管制冷机二维计算域划分示意图Fig.2 Schematic of 2D calculation meshes of the micro pulse tube refrigerator
1.2 物性设置
固体材料为铜和硅,其在250~380 K的比热容和导热系数可由文献[18]获得。流体为氦,其在0.2 MPa、250~380 K下的导热系数、黏度和定压比热等物性参数可使用REFPROP 9.1[19]软件检索。将获取的固体和流体物性参数进行关于温度的多项式拟合后,写入Fluent 19.0软件的物性库中。
1.3 区域条件和边界条件设置
模型中相关的区域条件与边界条件分别如表1和表2所列。

表1 区域条件(p=0.2 MPa)Tab.1 Cell zone conditions(p=0.2 MPa)

表2 边界条件Tab.2 Boundary conditions
交变流动情况下的pin和mout可写为一阶傅里叶变换的形式,如式(1)(2)所示:
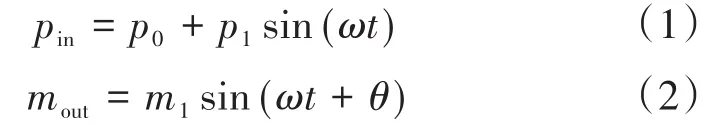
式中:pin为回热器热端入口的压力,MPa;mout为脉管热端的质量流量,kg/s;p0为制冷机内部平均压力,为0.2 MPa;p1为回热器热端压力振幅,MPa,由压电薄膜的振动幅度决定[11],受压电材料的性能限制,本文选取回热器热端的压比为1.1,由此可得p1为0.009 5 MPa;m1为热端换热器流至调相机构的质量流量幅值,kg/s,由回热器参数选定;θ为mout与pin的相位差,根据Radebaugh的建议[20],取为-60°;ω为圆频率,Hz;t为时间。薄膜的工作频率为500 Hz。
式(1)和式(2)通过 UDF(User-Defined Func⁃tions)编写并导入Fluent软件中作为pin和mout的边界条件,设定CHX壁面的温度为293 K,将HHX壁面、级后冷却器壁面、pin和mout温度设置为相同的热端温度,调整热端温度以进行后续工况计算。
1.4 数学模型
计算流场时选用RNG k-ε湍流方程。其控制方程[20]如下:

式中:P为湍流动能项,由湍流动能k决定;D为湍流耗散项,由湍动耗散率ε决定,m2/s2。u、v分别为x、y方向上的速度分量,m/s;νTu为湍流的运动黏度,m2/s;σk和σε分别为湍流动能和耗散率对应的有效普朗特数;Cε1和Cε1分别为确定的湍动经验系数。
级后冷却器、回热器、CHX和HHX均选用多孔介质模型,其控制方程[21]如下:

式中:Si为动量源项;∇p为压力梯度,MPa/m;Δn为单位厚度,m;μ为流体动力黏度,Pa·s;1/α为多孔介质黏性阻力因子,m-2;L为惯性阻力因子,m-1;ρ为流体的密度,kg/m3;vi为速度的笛卡尔分量,m/s。对式(5)取矢量大小后计算可得:

式中:Δp为压降,MPa;v为速度,m/s。对于多孔介质的阻力系数,可将其压降拟合成关于流速的关联式。通过流动条件下流体的黏度和密度,可确定1/α和L的值。对于本文中的硅基回热器,层剖面结构如图3所示。

图3 硅基微型回热器结构示意图Fig.3 Structure of the silicon-based micro-regenerator
根据已有实验数据[22]可得硅基回热器阻力系数f的关联式为:
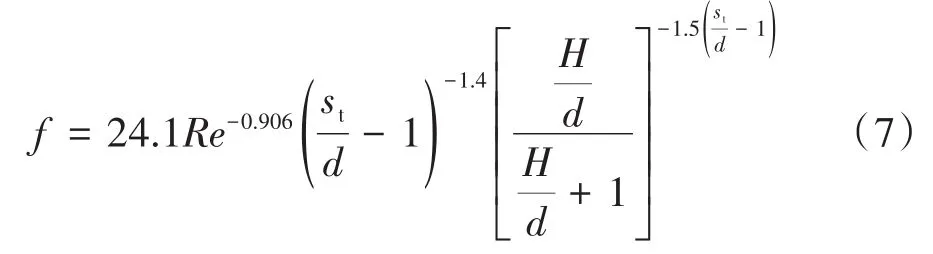
式中:H为硅基回热器的层间距,μm;d为柱状物的直径,μm;St为柱状物中心间距,μm。
雷诺数的表达式如式(8)所示。

阻力系数f与压降的关系为:

式中:N为与流体流动方向垂直的管排数。联立式(7)到式(9)可得到压降与速度的表达式(10)。
将式(10)计算得到的值拟合成如式(6)的形式,可得到不同回热器结构下1/α和L的值。表3列出了三种不同结构回热器的1/α、L和空隙率φ的值。对于级后冷却器、CHX和HHX采用上述相似的步骤也可得到相应的1/α、L和φ的值,如表4所列。
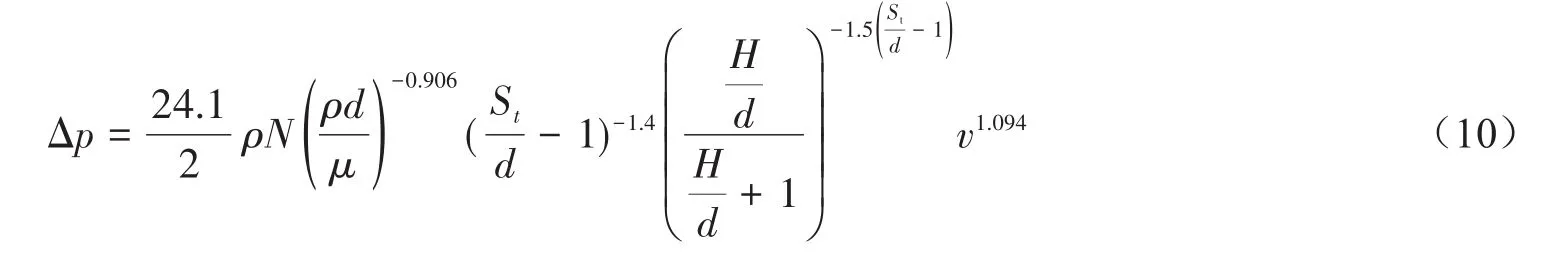

表3 工质为氦的回热器不同几何结构下的参数Tab.3 Parameters of micro-regenerator(He)with different geometry

表4 微型脉管制冷机不同部件1/α、L和φ的值Tab.4 Values of the components of the micro pulse tube refrigerator
1.5 求解器设置以及求解精度设置
由于脉管区域为湍流流场,且与制冷量计算直接相关,因此采用基于压力-速度修正的PISO算法。压力收敛格式为压力交错格式;密度、湍流动能和湍流耗散率均设置为一阶迎风格式;能量和动量设置为二阶迎风格式;时域传递为二阶隐式。时间步长为2.5×10-6s,每1 600步为一个周期。制冷机达到稳态时每周期记录CHX的温度和热流密度,每步长记录进出口和CHX位置的压力与质量流。
由于采用瞬态计算,本文中判断制冷机达到稳态的判据是:当CHX区域的面平均温度在前后两个周期的相对变化小于1×10-4K时,可以认为处于稳态工况。此时监测得到的CHX壁面上一周期内的净热流密度的平均值乘以CHX的表面积作为对应稳态下制冷机的毛制冷量。净制冷量则是在毛制冷量的基础上减去回热器热端和脉管段热端对冷端的导热损失,净制冷量和导热损失的表达式分别如式(11)和式(12)所示。

式中:QC和QC,net分别为脉管制冷机的毛制冷量和净制冷量,W;Qcond为通过回热器壁面和脉管壁面的导热损失,W;LRe和LPT分别为回热器长度和脉管长度,m;TH和TC为为热端和冷端的温度,K;kSi和ks分别为硅和不锈钢的导热系数,W/(m·K);ARe,w和APT,w分别为回热器壁面的截面积和脉管壁面的截面积,m2;T为温度,K。
1.6 网格无关性验证
热端温度设置为303 K,通过绘制网格数为6 992、8 236、9 680和14 575的4个算例,通过计算收敛后的冷端压力值进行网格无关性验证,结果如表5所列。由表5可见压力振幅的计算情况随网格数几乎不变,综合考虑计算精度与速率,选取计算的网格数为8 236。

表5 冷端压力振幅随时间和网格数的变化情况Tab.5 Variation of pcwith time and grid number
2 计算结果与讨论
2.1 常温区传统相位修正
根据理想回热器内部的质量流关系,回热器进出口质量流向量之间存在如式(13)所示关系。
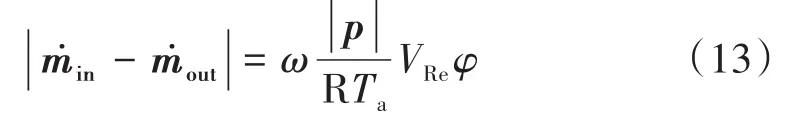
式中:ṁin为回热器进口的热端质量流量,kg/s;ṁc为回热器出口冷端质量流量,kg/s;||p为回热器平均压力幅值,MPa;R为气体常数,J/(kg·K);Ta为回热器的对数平均温度,K;VRe为回热器体积,m3。
根据低温制冷机的传统理想相位,回热器进出口质量流相位差为60°,回热器进口质量流领先压力波30°,脉管出口质量流相位落后冷端质量流相位30°,因此脉管出口质量流应与回热器质量流之间的关系如式(14)所示。
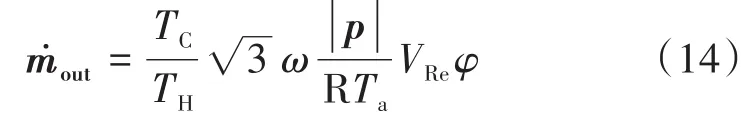
式中:ṁout为脉管热端的质量流量,kg/s。为验证低温温区回热器质量流与压力的理想相位关系在常温温区是否依然高效,算例的工作温区设为293~303 K,体积空隙率都为0.81,回热器热端压比为1.1,平均压力为0.2 MPa,工作频率为500 Hz,根据压力波与脉管出口质量流的相位差为60°可估算得到脉管出口的质量流幅值分别为0.433 g/s和0.139 g/s,以对应不同相位的工况。
当计算达到稳态时,分析两个算例的回热器进出口的质量流相位关系,结果如图4所示。如图4(a)所示的相位接近低温下的理想相位,即压力相位接近于回热器中部的位置,进口和出口质量流的相位与压力分别相差接近30°,而图4(b)所示的相位图显示,压力相位领先回热器进口质量流的相位,此时回热器进出口质量流横跨相位约15°。常温区相位计算的结果与文献[23]类似。进一步分析数据可得到冷端温度、制冷量和回热器入口声功,结果如表6所列。
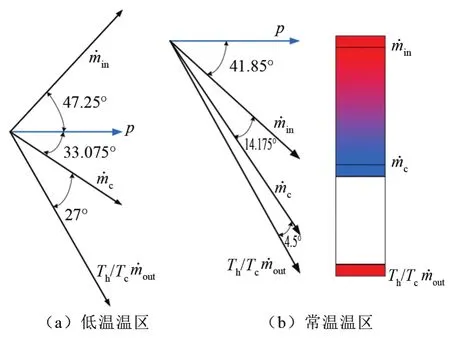
图4 293~303 K温区下微型脉管制冷机的相位图Fig.4 Phase diagram of the micro pulse tube refrigerator with a temperature difference of 293~303 K

表6 不同相位下微型脉管制冷机稳定时的冷端温度、净制冷量和回热器入口声功Tab.6 Cold end temperature,net cooling capacity and acoustic power into regenerator of the micro pulse tube refrigerator in different phase angles
从表6可以看出,图4(a)所示的低温理想相位并不能使得微型制冷机在常温区(293~303 K)制冷,而图4(b)所示的相位关系能够在该温区获得冷量,因此常温区的制冷相位与低温区存在较大不同[22]。在之后的计算中确定脉管热端的质量流量幅值为0.433 g/s,以便能够制冷。
2.2 回热器空隙率的影响
由式(13)可知,回热器的空隙率会影响进出口质量流的相位差。由于Fluent软件的计算精度为二阶,而硅基回热器的多孔介质模型表明,改变空隙率须通过改变硅基的N、H、St和d来实现,此时的影响不仅体现在质量流相位差上,还可能体现在压降上。对表3所列的空隙率分别为0.61、0.81、0.87和0.95的硅基回热器在293~303 K温区进行数值计算。稳定运行时,1个周期内的质量流、压力曲线以及相位图如图5~8所示。
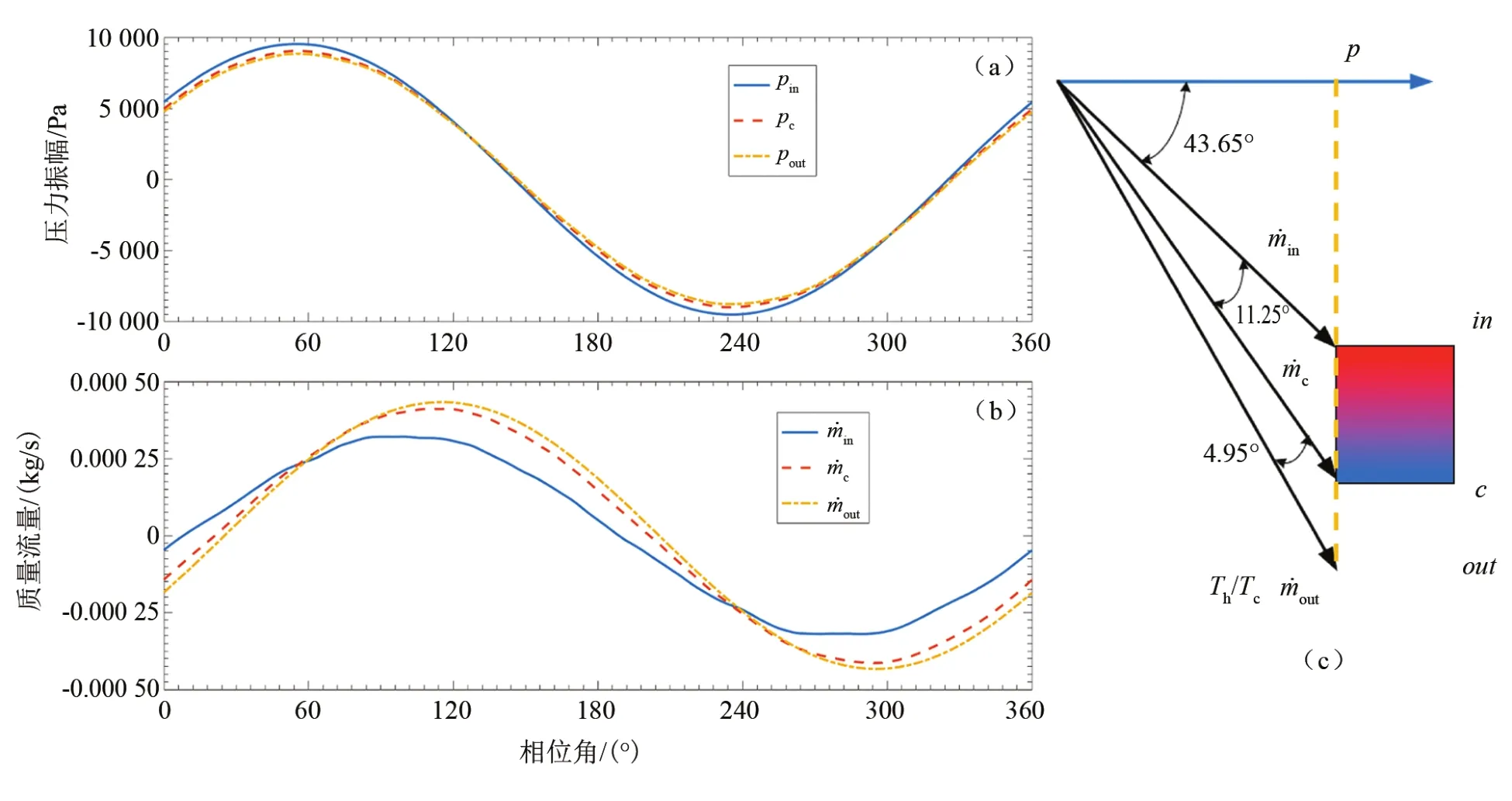
图5 293~303 K温区回热器空隙率为0.61时,制冷机稳态1个周期内质量流和压力振幅曲线以及相位图Fig.5 Mass flow,pressure amplitude and phase diagrams in the refrigerator during one cycle at 293~303 K with a porosity of regenerator 0.61

图6 293~303 K温区下回热器空隙率为0.81时,制冷机稳态1个周期内质量流和压力振幅曲线以及相位图Fig.6 Mass flow,pressure amplitude and phase diagrams in the refrigerator during one cycle at 293~303 K with a porosity of regenerator 0.81

图7 293~303 K温区下回热器空隙率为0.87时,制冷机稳态1个周期内质量流和压力振幅曲线以及相位图Fig.7 Mass flow,pressure amplitude and phase diagrams in the refrigerator during one cycle at 293~303 K with a porosity of regenerator 0.87

图8 293~303 K温区下回热器空隙率为0.94时,制冷机稳态1个周期内质量流和压力振幅曲线以及相位图Fig.8 Mass flow,pressure amplitude and phase diagrams in the refrigerator during one cycle at 293~303 K with a porosity of regenerator 0.94
在空隙率为0.61时,1个周期内回热器质量流量呈现出明显的高次谐波分量,这说明表3中黏性项的增加,使得连续性方程的数值解已经难以使用一阶傅里叶形式来表达。
当空隙率足够大时,质量流和压力的近似计算可以使用一阶傅里叶形式表达,这也说明当回热器内部的空隙率足够大的时候,压力和质量流符合一阶傅里叶的解析形式。综合图5~8的结果可以看出,硅基回热器内空隙率的增加引起了式(13)向量长度的增加,具体体现为回热器进出口质量流量对应的相角不断增加。由于回热器热端压力与脉管出口质量流的相位角是预设的,因此空隙率的增加将引起脉管段内部质量流相位的减小。为探究空隙率对微型脉管制冷机内部温度场的影响,使用Fluent软件对表3所列的四种回热器结构某一时刻温度分布进行计算,所得的云图结果如图9所示。

图9 293~303 K温区微型制冷机的回热器在不同空隙率下的典型温度场云图Fig.9 Typical temperature contours of the micro-refrigerator during at 293~303 K with different porosities of regenerator
图9包含了整机的温度云图分布,具体部件的几何位置在图中进行了说明。可以看出,在微型斯特林脉管制冷机尺寸确定的情况下,回热器空隙率与整机的温度云图之间存在两种极端情况:当回热器内空隙率较小时,从回热器冷端进入脉管的气流在截面上的温度分布均匀性较差,引起脉管段内的导热损失;当空隙率非常大时,回热器内部气体速度较大,进入脉管后膨胀进行的不完全,将出现气体活塞被进出脉管的气体射流击碎的情况,最终导致制冷机性能的恶化。为进一步分析回热器空隙率对制冷机性能的影响,调取不同空隙率算例下稳定后的制冷温度、压力和质量流监测点的数据,计算整理可得表7。为进一步分析空隙率与制冷机COP的关系,将计算结果绘制如图10所示。
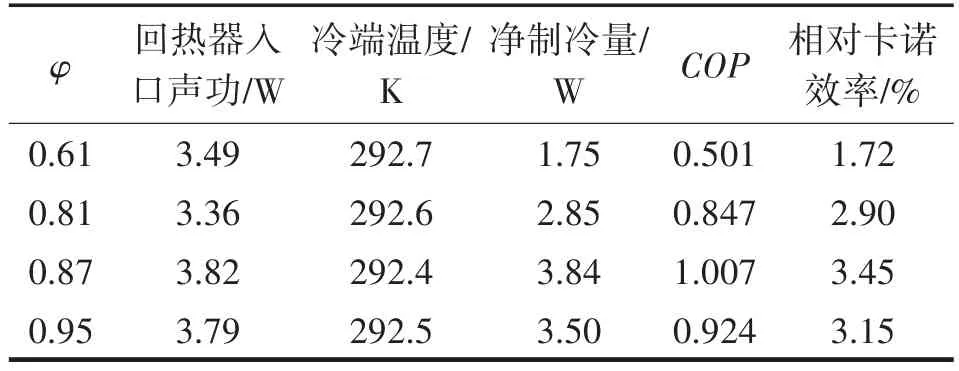
表7 293~303 K温区不同回热器空隙率下的制冷机稳态性能参数Tab.7 Steady state performance of refrigerators with different porosity of regenerator at 293~303 K

图10 293~303 K温区下微型制冷机回热器空隙率与COP和净制冷量的关系曲线Fig.10 COP and net cooling capacity of the microrefrigerator during at 293~303 K with different porositiy of regenerator
综合表7和图10的结果可以看出,制冷机的COP随空隙率升高先上升后下降。现有尺寸下,存在一个0.87左右的最优空隙率使得COP和相对卡诺效率达到最大值,该结果与文献[14]中提及的回热器最优空隙率结果接近。从整机优化角度来看,在空隙率较大的情况下需要适当增加脉管长度以实现内部气体活塞充分运动来提升性能。但具体优化细节还需要进一步研究。
2.3 制冷温度对制冷性能的影响
考虑现有加工精度和难度,选定硅基回热器的空隙率为0.81,保持冷热端的温差为10 K不变,分别调整冷端温度为293 K、313 K和333 K,来探究制冷温度对该结构制冷性能的影响。算例中记录制冷机稳态时1个周期内不同位置处的压力、质量流幅值。冷端温度为293 K、313 K和333 K的计算结果由分别如图6、图11和图12所示。

图11 313~323 K温区下回热器空隙率为0.81时,制冷机稳态1个周期内质量流和压力振幅曲线以及相位图Fig.11 Mass flow,pressure amplitude and phase diagrams in the refrigerator during one cycle 313~323 K with a porosity of regenerator 0.81

图12 333~343 K温区下回热器空隙率为0.81时,制冷机稳态1个周期内质量流和压力振幅曲线以及相位图Fig.12 Mass flow,pressure amplitude and phase diagrams in the refrigerator during one cycle at 333~343 K with a porosity of regenerator 0.81
从图6、图11和图12中可以看出,在温区为293~303 K和313~323 K时,回热器进出口质量流相位基本不变,质量流和压力的相位基本一致。当工作温区为333~343 K时,回热器进口质量流的计算出现了高次谐波项,并不如前两个工况一样呈现光滑的曲线。根据式(13)所示,回热器进出口质量流之差的向量大小随回热器内对数平均温度升高而降低,因此造成了进出口相位差随温度上升而减小的结果,这与模型计算结果的趋势一致。
调取温度、压力、质量流监测点的数据,计算整理可得如表8所示结果。可以看出,随着冷热端温度不断上升,微型制冷机净制冷量不断增加,但相对卡诺效率在不断降低,因此可以看出,未经过结构优化的微型制冷机工作在高温温区,尽管制冷量满足需求,但需要对相应温区的充气压力、相位等因素进行优化设计,才能保证较高的效率。

表8 不同工作温区下的制冷机稳态性能参数Tab.8 Steady state performance of refrigerators with different temperature range
3 结论
本文采用Fluent软件对基于硅基回热器的微型脉管制冷机进行了几何建模计算,研究结果表明:
(1)在传统低温温区的理想相位(回热器热端质量流领先压力波)下,微型脉管制冷机无法在293 K时提供制冷量。经过修正后的工作相位,即回热器热端质量流落后压力波的情况下,工作频率为500 Hz时,可在293 K提供2.85 W的制冷量,回热器热端入口声功为3.36 W,COP为0.847,相对卡诺效率为2.89%。上述结果验证了常温区下微型斯特林脉管制冷机正常工作的相位与传统低温温区相位不同的情况。
(2)微型硅基回热器空隙率对制冷机性能存在较大影响。随着回热器空隙率的增加,制冷机的COP先上升后下降,存在一个最佳空隙率。因此,改变回热器硅基的结构,使得空隙率接近最佳值,是提升制冷机性能的一种优化方式。同时计算发现,随着空隙率的减小,在回热器中的压力和质量流将会出现高次谐波分量使得性能迅速衰减和恶化。
(3)微型脉管制冷机的制冷量随工作温度上升而增加,但相对卡诺效率和COP都随温度上升而降低。计算结果表明:在500 Hz工作频率和现有回热器几何参数条件下,该微型脉管制冷机可在333 K、313 K和293 K分别提供3.15 W、2.87 W和2.84 W的制冷量,COP分别为0.687、0.785和0.848,相对卡诺效率分别为2.35%、2.68%和2.89%。根据目前条件下的计算结果,能够验证微型脉管制冷机在微型尺度与常温温区下具备制冷能力,但制冷性能上受到一系列现有条件的限制。对于回热器而言,运行频率越高,最优充气压力也越高,由于膜片最大形变幅度与硅基结构的强度等限制,无法在高运行频率下达到相应的最优充气压力。因此,基于硅基回热器的微型脉管制冷机的研制还需要材料方面的进一步研究。

