基于三次样条插值的几何精确曲梁单元

张志刚, 马新旋, 王才东, 郑华栋, 王良文

(郑州轻工业大学 河南省机械装备智能制造重点实验室,河南 郑州 450002)

随着新材料新技术的飞速发展,大变形部件的工程应用也越来越多,如风机叶片、大展弦比机翼、航天器可展天线和太阳能帆板等,甚至出现了利用弹性变形传递运动、力和能量的新型机构[1-2]。针对大变形梁建模问题,在多体系统动力学领域先后发展形成了两类最具代表性的方法:几何精确梁理论和绝对节点坐标方法(ANCF)。

几何精确梁理论[3-5]在刚性截面假设基础上引入大转动参数描述截面转动,也被称为大转动矢量法[6]。基于此方法提出的梁单元通常具有单元参数少、节点力物理含义清晰等优点,但由于常用大转动参数如欧拉角、卡尔丹角、罗德里格斯参数和转动矢量等是伪矢量,对这类参数独立插值会破坏应变独立性[7]。针对这一问题,Zupan等[8]将欧拉四元数用作截面大转动的描述,并推导了三维几何精确梁的平衡微分方程及其弱形式;Ghosh等[9]在四元数描述基础上提出了球面线性插值的梁截面转动离散策略。四元数应用可以保证几何精确梁理论中曲率应变的客观性,但截面转动独立插值方法构造出来的单元属于Timoshenko梁模型,该方法用于求解细长梁问题时会遇到剪切闭锁[10]。针对空间细长梁,Zhao等[11]构造了一种严格满足梁截面与形心线垂直关系的几何精确梁单元,避免了剪切闭锁的出现;Fan等[12]利用四元数球面线性插值得到梁截面转动场,在忽略轴向应变的前提下,依据Euler-Bernoulli梁变形假设由转动积分得到了形心位移,其中,三维梁单元中间节点参数仅包含表征截面转动的欧拉四元数,因而总体参数大幅减少。对于平面问题,梁内部节点只有截面方向角一个自由度[13-14]。但由于位移场需要通过转动场积分递推得到,计算量大,且处理节点位移约束时也较为烦琐。

Shabana[15]提出的ANCF梁单元采用无转动参数方法,通过选取表征梁截面变形和方向的位置梯度矢量代替转动参数作为单元参数,避免了大转动描述引发的数值问题。此外,ANCF梁单元节点力计算程式化高,并且具有质量矩阵为常数阵、离心力和科氏力为0、约束方程描述简单等优点。然而,ANCF梁单元节点参数通常成倍于传统梁单元,由此引入的截面变形与拉压、弯扭耦合等复杂高阶模态也会严重影响仿真计算效率。冗余自由度的存在也赋予了ANCF单元描述复杂几何构型的能力,其单元几何描述与计算机辅助设计(CAD)通用的B样条和非均匀有理B样条(NURBS)之间存在线性映射关系[16],可以方便地实现ANCF网格与CAD模型的转换,而这恰是现有几何精确梁单元不具备的。

本文从减少整体参数、方便与CAD几何描述融合出发,提出了一种几何精确平面曲梁单元。基于三次样条插值构造了形心线变形场,并根据Euler-Bernoulli梁变形理论,由形心线切向确定了梁截面的方向。由于单元内部节点参数仅包含位置矢量而不含转动参数,因此单元自由度大幅降低。本文单元精度和求解效率通过典型算例加以验证。

1 平面曲梁的三次样条插值

曲梁在适应特定空间环境、满足特殊工况等方面具有独特优势,在工程中有重要应用。依据刚性截面假设,梁的几何构型可由形心线运动与截面转动描述。对于考虑初始弯曲的平面Euler-Bernoulli梁,选取节点处的位置矢量r0,r1,…,rn和首末两端节点的轴向位置梯度矢量r0,s、rn,s为总体参数,如图1所示。

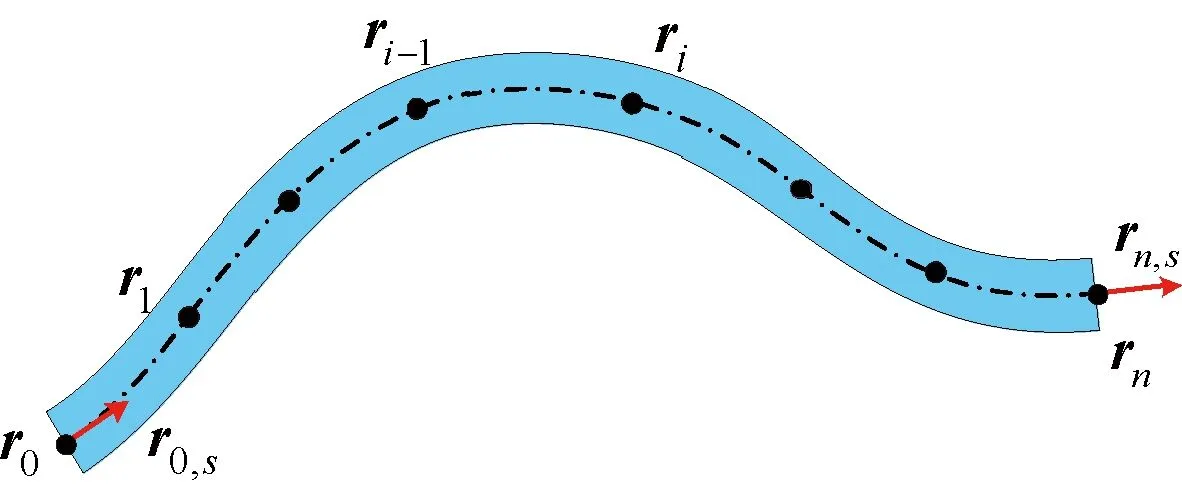
图1 平面曲梁的几何构型

Euler-Bernoulli梁的截面始终与形心线切向垂直,这里采用三次样条插值近似梁的形心线。由三次样条性质可知,在第i段弧长坐标s∈[si-1,si]上任一点的位置矢量r可以表示为

(1)

式中:Li=si-si-1为第i段对应弧长;ξ=(s-si-1)/Li为归一化参数。Hermite基函数为

(2)

除端部节点外,式(1)中出现的中间节点参数ri,s需要利用样条函数连续性条件确定。根据三次样条函数性质可知,中间节点处满足二阶导数连续,即

(3)

式中:Ki=Li/Li+1为相邻梁段的弧长比。

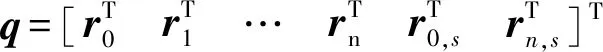
(4)

(5)

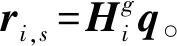
(6)

(7)

2 平面曲梁的整体控制方程

在上述整体形心线三次样条插值基础上,依据几何精确梁理论推导平面曲梁的整体动力学方程。

2.1 内力虚功率

根据Euler-Bernoulli梁变形假设,梁截面始终与形心线切向保持垂直。在平面曲梁第i段内,记形心线上任意点处的切向单位矢量为ni,法向单位矢量为ti,如图2所示。

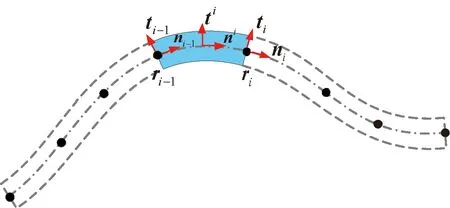
图2 平面曲梁内第i段单元

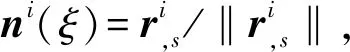
梁单元内任意点处的轴向应变εi和形心线曲率κi可以表示为

(8)

据此可将平面Euler-Bernoulli梁的内力虚功率表示为

(9)

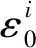
利用积分与求和运算的可交换性整理得到平面曲梁的内力虚功率为

(10)

其中节点力列阵为

(11)

2.2 切线刚度阵

曲梁的切线刚度阵K可以通过对广义节点力列阵(式(11))求偏导得到,即K=∂Fs/∂q=Kt1+Ktσ,其中Kt1为材料刚度矩阵,Ktσ为几何刚度矩阵。

(12)

2.3 惯性力虚功率

平面Euler-Bernoulli梁的惯性力虚功率是截面跟随形心平动和绕形心转动的虚功率之和。由式(6)可知,梁截面形心速度和加速度分别为

(13)

梁截面的转动角速度可以表示为

(14)

对式(14)再求一次时间导数可得到截面角加速度:

(15)

因此,平面Euler-Bernoulli梁的惯性力虚功率为

(16)

式中:mi为第i段曲梁的质量;Ib为将截面绕形心主轴的惯性矩。将形心速度和加速度(式(13))、截面转动角速度(式(14))和角加速度(式(15))代入曲梁整体惯性力虚功率(式(16)),整理得

(17)

其中,平面曲梁的整体质量阵M和惯性力余量列阵Fa分别为

(18)

2.4 外力虚功率

不失一般性,假设平面曲梁上受到的外力包括作用在节点i处的集中力fi,首末两端节点处的集中力矩为m0和mn以及梁弧长域内第i段的分布力pi(ξ),则外力的虚功率可以表示为

(19)

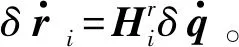
根据式(14),曲梁两端节点处的虚角速度分别为

(20)

将其代入外力虚功率(式(19))可得

(21)

其中广义外力列阵为

(22)

2.5 整体控制方程

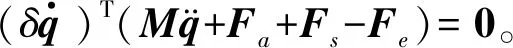
(23)

3 数值算例

本节将通过对典型数值算例的求解来验证单元精度和计算效率。静力学算例采用MATLAB非线性方程求解器fsolve计算,动力学算例采用基于向后差分法(BDF)的刚性微分方程求解器ode15s仿真求解。

3.1 静力学验证1(直梁)

悬臂梁在端部集中载荷作用下的几何非线性问题是验证梁单元精度的典型算例。设梁长L=1 m,梁截面面积Ab=0.05×0.05 m2,材料弹性模量为E=2.10×1011Pa,如图3所示。

图3 悬臂直梁

先研究悬臂梁在端部横向力作用的变形问题,记自由端沿X方向和Y方向的位移分量分别为u和v。将悬臂梁等分为10个单元,利用分步加载方法将计算得到的自由端位移数值解与文献[17]高精度椭圆积分解进行对比,如表1所示。

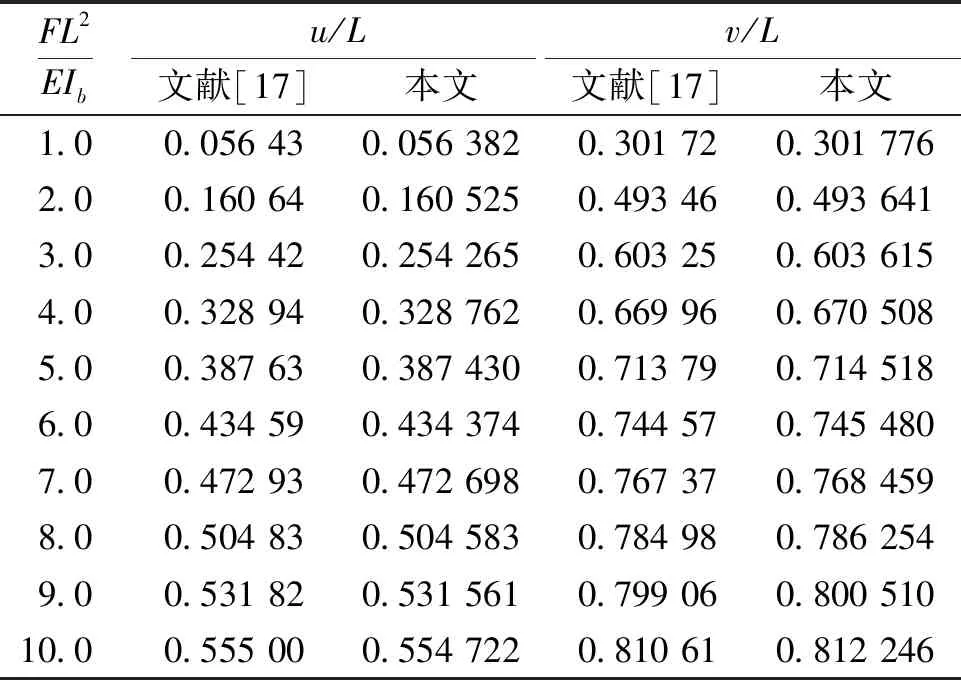
表1 端部集中力作用下悬臂梁的位移

对比表1中的数值结果可知,所得数值结果与文献[17]最大误差小于0.2%,这证明了本文单元在选取较少参数的同时也能保证计算精度。图4给出了悬臂梁受端部横向力作用下的位移-载荷曲线。

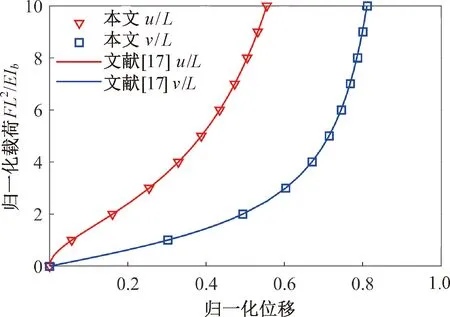
图4 悬臂梁受杆端横向力作用位移

悬臂梁纯弯曲问题的位移解析解存在,当最大弯矩M=2πEIb/L时将被弯成一个圆环。依然将悬臂梁等分为10个单元,将本文得到的自由端节点位移数值解与解析解进行对比,如图5所示。

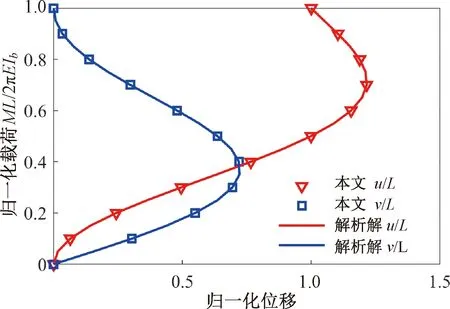
图5 悬臂梁受杆端弯矩作用的位移

由悬臂梁端部位移的数值解与解析解比较可知,当直梁被弯成圆时,端部节点位移的最大误差仍小于0.01%。图6展示了在不同弯矩作用下对应的悬臂梁变形过程。

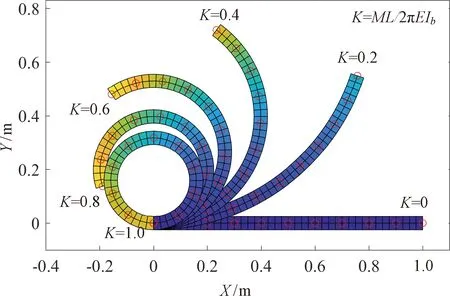
图6 悬臂梁的纯弯曲大变形

3.2 静力学验证2(环形梁)

本算例考察了所提方法对于带有初始屈曲大变形梁的静力学精度问题,这里研究一端受固定约束另一端自由的环形梁。设环形梁半径R=1 m,截面面积Ab=0.1×0.1 m2,材料弹性模量E=2.10×1011Pa,梁自由端施加沿逆时针方向的弯矩M,如图7所示。

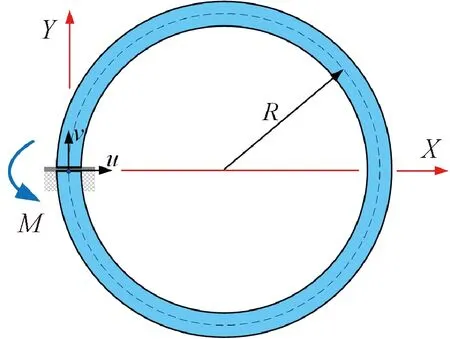
图7 环形梁的纯弯曲

分析可知,当弯矩M=2πEIb/L时,悬臂环形梁将变成为直梁;进一步增大弯矩至M=4πEIb/L时,环形梁将被反向弯曲为一个圆。仍将环形悬臂梁等分为10个单元,通过迭代计算得到的自由端节点X方向位移u和Y方向位移v的数值解,如图8所示。

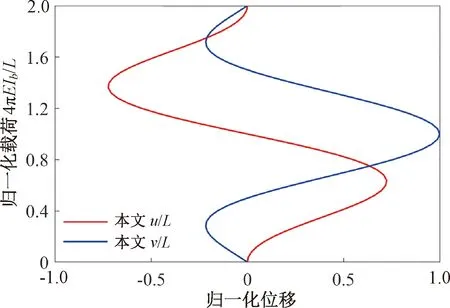
图8 环形梁受杆端弯矩作用的位移

由图8可知,当最大弯矩M=4πEIb/L时,采用本文方法得到的自由端节点能够经过反向弯曲又回到了初始位置,此时对应的2个方向的位移均为0。图9显示出了环形梁的变形过程。

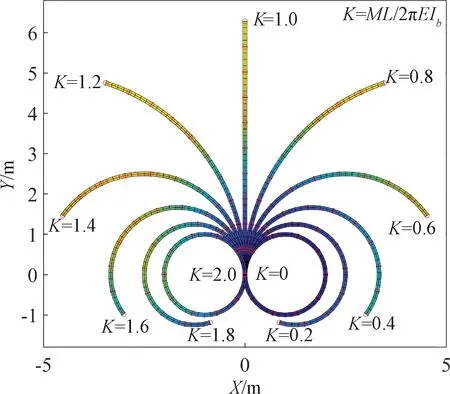
图9 环形梁的纯弯曲变形

3.3 动力学验证(曲梁单摆)

这个算例用来考察用本文单元求解曲梁动力学问题时的计算精度和效率问题。为此研究曲梁单摆自由下落问题,设曲梁弧长L=π m,形心线半径R=3 m,其对应圆心角为60°的一段圆弧。曲梁截面面积Ab=0.2×0.2 m2,弹性模量E=6.9×108Pa,泊松比μ=0.27,在竖直方向重力g=9.81 m/s2作用下由图10所示位置自由下落。

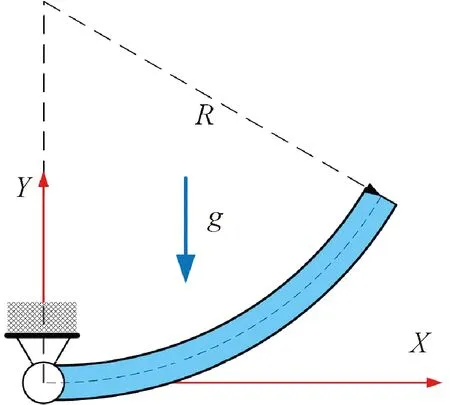
图10 曲梁单摆

选取平面ANCF梁单元[18]的仿真数值结果作对比,该单元的节点参数包含位置矢量和2个方向的梯度矢量共6个自由度。将曲梁等分为8个单元,设定仿真时间为1 s,绝对误差εa=1.0×10-4,相对误差εr=1.0×10-3。将采用本文所提几何精确曲梁单元建模求解得到的单摆末端节点X方向坐标和Y方向坐标的数值解与ANCF梁单元对应数值解进行对比,如图11所示。

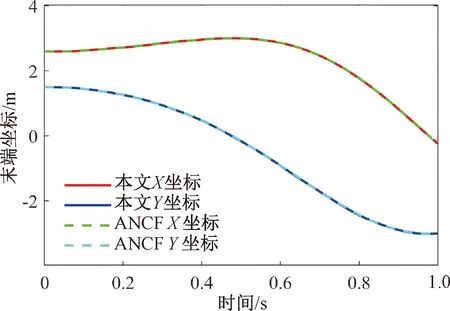
图11 曲梁单摆模型的末端位置坐标

从图11可以看出,本文方法得到的数值结果与平面ANCF梁单元结果十分吻合,这说明对于含初始弯曲梁的刚柔耦合动力学问题,采用本文提出的几何精确曲梁单元具有良好的计算精度。

对比仿真求解时间:在相同配置电脑上进行计算,采用本文单元完成仿真耗时295.3 s,而采用相同单元数目的平面ANCF梁单元需要5 941.8 s。在这个算例中,本文单元计算效率是ANCF梁单元的20倍以上。在同样是划分8个单元共计9个节点,在添加约束前采用本文单元建模共有22个参数(包含9个节点处的位置矢量参数和首末2个节点的轴向梯度矢量参数),而对应的ANCF梁单元模型自由度则多达54。这也从参数数量方面初步揭示了本文单元求解效率更高的原因。

上述算例表明,本文基于三次样条插值提出的几何精确曲梁单元在保证计算精度的同时,在计算效率方面也具有明显优势。

4 结论

现有包含节点转动参数的几何精确梁单元通常采取对形心线运动和梁截面转动进行独立插值的策略,不仅在分析细长梁时会遇到剪切闭锁问题,且有限元网格无法与CAD几何模型直接转换。选取节点位置矢量和梁两端节点处的轴向位置梯度矢量为总体参数,提出了一种不含节点转动自由度的平面几何精确曲梁单元。利用三次样条插值近似梁的形心线变形,而梁截面转动则完全由形心线切向确定。通过对典型算例的求解,可以得到如下结论。

(1)相较于传统几何精确梁,本文单元节点参数不含转动自由度,单元总体自由度大幅降低;在同等单元数量情况下,计算效率显著提升。

(2)梁的形心线由三次样条插值近似,单元内部节点处轴向应变的连续性也得到了满足,且可与CAD几何模型进行转换。构造的耦合变形场能够保证保持梁截面与形心线切向的垂直关系,因此剪切闭锁问题不会在单元应用中出现。

(3)采用的研究方法可以进一步推广到大变形空间梁单元和板壳单元的研究。