高中数学中三角函数的解题技巧
——以三角函数的图形与性质为例
罗培洲
(福建省龙岩市连城县朋口中学,福建 龙岩 366211)
高中数学的课堂教学中,三角函数占据着重要地位与作用,再加上三角函数有着一定的概念性与抽象性特征,其学习难度相对较大.这就使学生在对三角函数进行解题时,容易出现错误,导致学生对于三角函数相关知识的学习丧失自信心与兴趣,由此可知,学习、掌握与三角函数题有关的解题技巧就极为重要.三角函数的前提与基础是几何当中的单位圆与相似性,而研究方法是代数的图形与变形分析,因此,在对三角函数的试题进行解答时,需注重代数知识与几何知识的有效联合,准确把握其解题技巧,从而使学生的解题效率与准确率得到有效提高.
1 三角函数的图形解题技巧
1.1 明确数量关系
一般来说,以三角函数的图形求解相关数量关系,其主要分成将数量转变成图形、将图形转变成数量的两种思路.依据上述两种思路,从图形转变为数字的重点是针对既定几何图形,通过对图形进行详细观察,精确找出图形中隐藏的数量关系,从而使学生更高效地解决数学问题[1].
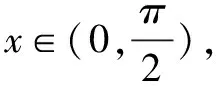


图1 函数f(x)=tanx的图象
1.2 以三角函数的图形求取最值
求取最值是三角函数中典型的难题.大多数状况下,三角函数的最值求取都会给出某个区域的具体函数式,按照一定的关系,求解出该区域内三角函数的最值.而函数图像则能直观地展示出函数的最大值或者最小值,因此,在求解最值的时候,与函数图象相结合,可有效简化最值求解的难度[2].

解析在解决本题的时候,可将给出的函数转化为二元一次函数,并按照要求的区域,画出的对应的函数图像,则能快速解决本题,即将题干给定的函数做出如下转变,y=cos2x+sinx=-sin2x+sinx+1,并依据题干条件,画出对应的函数图象,详见图2.

图2 函数y=-sin2x+sinx+1的图象

2 三角函数的性质解题技巧
2.1 以三角函数的单调性进行解题
一般来说,三角函数当中的余弦函数、正弦函数、正切函数等位于相应区间内容都具有单调性,在对高中数学题进行处理与解答时,教师可指导学生与三角函数的单调性结合进行解题,如三角函数式大小、三角函数的定义域和单调区间等[3].
例3若α与β都是锐角,且存有sinα 奇偶性为三角函数的性质之一,是相对于定义域的,函数通常可分成偶函数、奇函数、既奇又偶函数、非奇非偶函数,常常可通过奇偶性进行三角函数的值域、最值、定义域、解析式、单调区间等相关问题进行解决[4].数学教师在指导学生通过三角函数具备的奇偶性进行解题时,首先,可引导学生明确函数定义域是不是关于原点对称,并画出函数图象;其次,按照三角函数具备的奇偶性进行思考和分析,以求解出值域、最值、定义域以及解析式等相关问题. 三角函数具备的有界性主要指若存有常数m与M,想要使函数y=f(x)且x∈D,那么则符合m≤f(x)≤M,且x∈D,则存有函数y=f(x)位于D内有界,当中的m为其下界,M为其上界.有界性为正弦函数和余弦函数共同具备的性质,其适合对函数的最值与值域等相关数学问题进行求解.高中数学的解题过程,教师可引导学生通过三角函数具备的有界性,引导学生与三角函数具备的单调区间、最值、定义域、值域结合,明确解题思路,优化其解题方法. 解析本题解答时,可先将三角函数中的常数实施分离,然后依据三角函数具备的有界性,及函数隐含定义域,对函数最值加以确定. 三角函数具备的周期性,函数值在重复出现的时候,自变量x的增加值就会成为函数周期,实际上讲,则针对函数y=f(x),若存有不是0的常数T,促使x取其定义域内的某个值,f(x+T)=f(x)均成立,此时,就需将函数y=f(x)称作为周期函数,不是0的常数T则称作为该函数的周期.在求解函数问题的时候,准确把握其周期性,可帮助学生更简单、直接地解决相关函数问题. 综上所述,高中数学的课堂教学中,促进学生对三角函数的具体解题思路与技巧掌握,既能确保解题的准确率,又能促进学生的解题效率提高.鉴于此,数学教师需充分认识到三角函数相关内容的重要性,在实现基础知识与公式巩固的同时,掌握相关解题技巧,促进学生解题思路的优化,从而使学生的解题效率得到明显提高.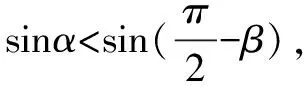
2.2 以三角函数的奇偶性进行解题


2.3 以三角函数的有界性进行解题


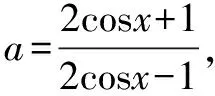
2.4 以三角函数的周期性进行解题



