求解一类3×3块鞍点问题的参数化块移位分裂预处理子

李 剑,张 娜,李瑞霞

(陕西科技大学 数学与数据科学学院, 陕西 西安 710021)

0 引言

考虑以下3×3块大型稀疏线性系统的快速求解:

(1)

式中:矩阵A∈Rn×n是对称正定的,矩阵B∈Rm×n和C∈Rp×m都是行满秩的,u∈Rn、v∈Rm、w∈Rp是给定的向量。这些假设保证了线性系统(1)的解的存在唯一性[1]。 通过以下两种形式的划分:

(2)

和

(3)

可以发现,3×3块线性系统(2)可以归结为经典鞍点问题[1]。而由于线性系统(3)中的(2,2)块是反对称矩阵,而(1,2)块是秩亏的,使其不同于传统鞍点问题。对于具有如此特殊分块的3×3块线性系统(1),由于其形似鞍点或双鞍点的结构,故也称为双鞍点问题。它广泛来源于工程应用和科学计算中的大多数问题,如约束二次规划[2]、椭圆偏微分方程的混合有限元方法[3]、计算流体动力学[4-5]以及最小二乘问题[6]等。

近年来,为了提高Krylov子空间方法求解传统鞍点系统的收敛速度,已经有很多预处理子被学者们陆续提出,如HSS预处理子及其变形[7-8]、移位分裂预处理子[9]、结构预处理子[10]等。但是考虑到结构上存在的差异,传统求解鞍点问题的预处理子并不能直接应用于双鞍点问题,因此寻找新的有效预处理形式是非常有必要的。

最近,针对双鞍点系统(1)的快速求解,HUANG等[11]提出了两个块对角(Block-Diagonal,简称BD)预处理子:

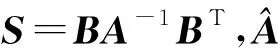
文献[12]分析了相应预处理矩阵的谱性质,表明这些预处理子会显著加快GMRES方法的收敛速度。但当内部系统被不精确求解时,计算时间会急剧增加。ABDOLMALEKI等[13]提出以下形式的块对角预处理子:

与HUANG等[11]提出的块对角(BD)预处理子相比,该预处理子的主要优点是不涉及Schur补矩阵,所以计算过程易于实施。作者从3×3分块矩阵的本征系统得到了一个三次方程,给出了相应预处理矩阵的特征值的分布范围。

此外,CAO[14]基于矩阵分裂,得到了一类移位分裂(Shift-Splitting,简称SS)预处理子:

式中:α>0是给定的常数,I是具有适当维数的单位矩阵。作者证明了相应迭代法的无条件收敛性,并给出了相应预处理矩阵的特征值分布范围。与文献[11]提出的块对角预处理子相比,移位分裂预处理子在计算效率上表现出良好的性能。

总的来说,虽然块对角预处理子M不涉及Schur补矩阵的计算,但与系数矩阵A的近似程度不高。而移位分裂预处理子PSS在计算过程中虽然与系数矩阵A的近似程度较高,但又涉及Schur补矩阵的求解。因此,构造不涉及Schur补矩阵的计算且与系数矩阵的近似程较高的预处理子,对于快速求解线性系统(1)是非常有意义的。

本文基于块对角预处理子M的构造特点,并结合移位分裂的思想,提出一种新的不涉及Schur补计算的参数化块移位分裂预处理子,用以求解线性方程组(1)。该预处理子具有易于实现且计算效率高等特点。此外,给出预处理矩阵特征值的上下界,并通过数值算例验证新预处理子的有效性。

1 一类新的参数化块移位分裂预处理子

将系统(1)中的系数矩阵A0进行如下分裂:

式中:α、β>0为迭代参数。该分裂可导出如下形式的块移位分裂预处理子:

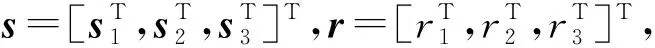
(4)

由此,预处理子P的算法实现过程如下:

算法1 求解Ps=r

1.求解As1=r1;

2.求解(αI+βBBT+CTC/α)s2=r2+CTr3/α;

3.计算s3=(r3-Cs2)/α。

算法1表明,利用预处理子P加速Krylov子空间方法来求解线性系统(1)时,只涉及以矩阵A和αI+βBBT+(1/α)CTC为系数矩阵的子线性系统的求解,不涉及显式Schur补的运算,可期望达到较高的计算效率。一般来说,预处理矩阵的谱分布越聚集,Krylov子空间方法的收敛速度就越快,下面给出预处理矩阵的谱分析。

引理1[15]设

是一个复系数一元多项式,λ是p(z)的任意根,那么|λ|满足以下不等式(柯西上下界):

|λ|≤max{|a0|,1+|a1|,…,1+|an-1|}。

定理1 设A∈Rn×n是对称正定矩阵,B∈Rm×n和C∈Rp×m都是行满秩矩阵,λ为预处理矩阵P-1A的特征值,[u*,v*,w*]*为相应的特征向量,则预处理矩阵P-1A有n个特征值为1,剩余的特征值分布范围如下:

(5)

式中:

λmin(BBT)≤b≤λmax(BBT),

λmin(CTC)≤c≤λmax(CTC)。

证明考虑广义特征值方程P-1Az=λz,即

式中:λ是P-1A的特征值,z=[u*,v*,w*]*是相应的特征向量,通过计算得到

(λ-1)Au-BTv=0,

(6)

Bu+λ(αI+βBBT)v+(1-λ)CTw=0,

(7)

(λ-1)Cv+αλw=0。

(8)

由于预处理矩阵P是非奇异的,故λ≠0。首先令u=0,则BTv=0,由B是行满秩矩阵可知,v=0。又因α≠0,由式(7)可得w=0,这与[u*,v*,w*]*是特征向量相矛盾。接着令u≠0,v=0,则由式(6)和式(8)可以推断出

(λ-1)Au=0,αλw=0,

这表明λ=1,其相应的特征向量的形式为[u*,0,0]*且u∈null(B),则预处理矩阵P-1A有n个特征值为1。故令u≠0,v≠0,由式(6)可知λ≠1。而A是非奇异的,由式(6)得

由式(8)得

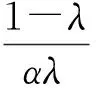
代入式(7)得

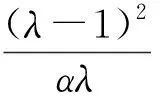
(9)

等式(9)两边同时乘αλ(λ-1)v*/(v*v),可得

进一步计算可得到以下关于λ的一个三次方程:

λ3(α2+αβb+c)-λ2(α2+αβb+3c)+λ(αa+3c)-c=0,

(10)

式中:

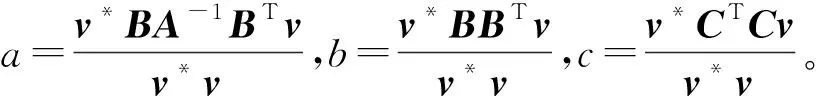
(11)

对于任意具有实特征值的方阵Φ,其最小和最大特征值分别用λmin(Φ)和λmax(Φ)表示,由式(11)以及文献[16]可得a、b、c的上下界:

λmin(BBT)≤b≤λmax(BBT),

λmin(CTC)≤c≤λmax(CTC)。

为了得到点(1,0)附近特征值的聚类性质,令μ=λ-1,式(10)可改写为以下形式:

根据引理1,可以得到μ的柯西下界和上界,进而得到λ的柯西下界和上界(式(5))。证毕。

2 数值实验

本节通过数值算例比较新提出的预处理子与已有预处理子的有效性。所有的数值实验都是在装有Intel(R) Core(TM) i7-8700 CPU @3.20 GHz 3.19 GHz 8.00 GB的电脑上使用Matlab R2019b进行计算。给出数值例子来分析新的块移位分裂预处理子的性能,z(0)的初始值设置为零向量,并在最大迭代次数kmax=1000时停止;或满足相对残差限时停止,

例1考虑3×3块鞍点问题(1),其中

B=(I⊗FF⊗I)∈Rp2×2p2,

C=E⊗F∈Rp2×p2,

且

E=diag(1,p+1,…,p2-p+1),

⊗表示Kronecker张量积,h=1/(p+1)为网格尺寸,总维数为4p2,右端向量b=(1,1,…,1)T∈R4p2。

数值实验是通过设置6个递增的剖分p=16、32、64、128、256、512生成的。表1给出了6种预处理子加速GMRES的数值结果,其中IT表示迭代次数、CPU表示计算时间、RES表示相对残差,符号“—”表示超过最大迭代次数或者超出存储需求。

表1 不同预处理子的数值结果Tab. 1 Numerical results of different preconditioners

对于预处理子M,设置α=0.001和β=1。对于预处理子PSS,设置α=0.01。而设置α=0.000 01和β=0.001作为本文提出的预处理子P的实验最佳选择。从表1可以看出,在迭代次数方面,新提出的预处理子P优于PBD2预处理子和M预处理子;在计算时间方面,新提出的预处理子P优于其他预处理子。特别地,在剖分p=256和p=512时,计算时间仍然有较优的结果,计算效率高于目前已有的预处理子。

图1分别绘制了当p=16时系数矩阵A0在PBD2、P2、P3、M、PSS、P作用下的预处理矩阵的特征值分布。可以看出,新提出的预处理矩阵P的特征值具有较好的聚集性。

图1 不同预处理子的特征值分布图(p=16)Fig. 1 Eigenvalue distribution of different preconditioners (p=16)

3 结束语

针对一类3×3块鞍点问题,提出了一种新的不涉及Schur补的参数化块移位分裂预处理子。与现有的预处理子相比,该预处理子易于实现且具有计算上的优势。文中讨论了相应预处理矩阵非零特征值的分布范围及特征值1的代数重数。数值结果表明,所提出的预处理子是非常有效的,特别是选取了合适的参数值之后,可以很大程度上提高Krylov子空间方法的收敛速度。