考虑形状分布特性的聚能射流侵彻作用规律研究

方一舟，张先锋，熊玮，冯可华，刘闯，葛小雷

（1.南京理工大学 机械工程学院，江苏，南京 210094；2.江苏永丰机械有限责任公司，江苏，南京 210014）

随着国外坚固类导弹/制导炸弹及低易损性炸药的应用与发展，迫切需要研究和发展新型防空反导战斗部技术.该类战斗部往往采用厚壁结构作为其壳体以更大程度地消耗毁伤元的能量，且内部装填具有低易损性的炸药，以更大程度地降低后续毁伤元的引爆能力.为了尽可能使反导拦截做到“命中即毁”，聚能装药以其强大的毁伤效能，常常作为防空反导作战中一种重要的毁伤元.聚能装药爆轰后形成的聚能射流贯穿厚壁结构后的剩余射流头部参量与剩余动能情况与其对壳内炸药的引爆能力密切相关，其形状特性对其侵彻靶板后剩余射流头部参量及剩余动能有着直接的影响.所以，研究考虑形状分布特性的聚能射流侵彻作用规律对防空反导聚能战斗部的结构设计和优化具有重要的指导意义.

近年来，学者们针对聚能射流开展了大量的研究工作.在聚能射流侵彻孔型计算方面，DIPERSIO等[1-2]给出了聚能射流侵彻金属靶板的侵彻孔径计算模型，简称为SDM 模型，并考虑了炸高对射流侵彻的影响.WOLFGANG 等[3]在SDM 计算模型的基础上对其进行了优化，得到了更为准确的聚能射流侵彻靶板的孔型计算模型，并研究了炸高对其侵彻孔径形貌的影响；SZENDREI[4]在聚能射流径向扩孔方面率先给出了一个解析表达，他认为射流侵彻的轴向压力必影响射流扩孔的初始径向压力，射流扩孔滞止压力与靶材扩张速度的关系可视为射流侵彻过程中弹靶交界处压力与侵彻速度关系的径向化，其结论一直被众学者沿用至今.HELD 等[5-6]修正了SZENDREI 的方程，形成Szendrei-Held 扩孔方程，发现计算模型的预测值总是小于试验结果，在高速侵彻工况下误差尤为明显.王静等[7]对在射流侵彻作用下靶板的径向响应过程进行了分析，基于虚拟原点概念推导了运动过程中射流径向尺寸变化规律，对射流侵彻过程中孔道孔径的变化规律进行了预测，分析得到了靶板在射流的侵彻作用下所形成孔道孔径随侵彻深度及孔道孔径随侵彻时间的变化规律.徐斌等[8]、余庆波等[9]、王芳等[10]、肖强强等[11]先后开展了不同装药结构对不同材料靶板的侵彻试验及理论研究，建立的侵彻深度预测模型具有一定的可靠性，但并未对侵彻孔型开展深入的分析；马雪亚等[12]开展了不同药型罩材料下的静破甲特性分析；陈兴等[13]探究了药型罩结构参数对杆式射流水下侵彻作用的影响；王成等[14]开展了聚能装药对混凝土靶板的侵彻研究，将混凝土靶板的侵彻孔型近似等效为漏斗坑与隧道区，探究了各装药参数对侵彻孔型的影响.在聚能射流形状描述方面，LAMBERT等[15]把具有速度梯度的射流假设为一个线性速度杆，用来描述虚拟原点坐标系中理想射流的侵彻情况；SVIRSKY 等[16]开展了线性铜杆对不同有限厚金属靶板的侵彻试验，通过试验观测获得了线性铜杆穿透有限厚靶板后的剩余速度与穿透靶背自由面时的射流长度损失，建立了该过程的数学模型，得出了半经验公式.WOFGANG 等[3]通过试验观察与数值拟合结合的方法将射流半径与该处的微元速度进行联系，得到了一种用来描述射流形状的非线性关系.在聚能射流冲击引爆方面，HELD 等[17-18]通过不同装药口径的聚能射流对B 炸药开展了一系列的引爆试验，根据试验结果，HELD 提出当射流头部参数v2d大于引爆阈值时，炸药将被引爆.魏继锋等[19]、宋乙丹等[20]分别开展了聚能射流冲击引爆不同炸药的数值模拟及试验研究，结果表明采用HELD 引爆判据可以较为准确地预测聚能射流对炸药的引爆情况.

综上所述，国内外众多学者开展了大量的关于聚能射流侵彻的理论计算及试验研究，对于考虑形状分布特性的聚能射流侵彻作用的研究具有重要的支撑意义.但现有的聚能射流侵彻孔径理论并未针对聚能射流的形状进行深入的分析，并且在射流形状描述方面，学者们大多将聚能射流形状考虑为线性铜杆或采用射流微元半径与微元速度关联的方式来表征射流的形状，并未考虑不同形状分布特性的聚能射流对侵彻作用的影响.为进一步分析不同形状分布特性的聚能射流对其侵彻靶板及后效剩余射流参数的影响，基于虚拟源点假设，考虑射流形状分布及飞行过程中的拉伸运动，建立考虑射流形状的射流侵彻计算模型，开展聚能射流侵彻及X 光试验，进一步分析不同形状对聚能射流侵彻不同厚度有限厚靶板靶后剩余射流头部参量及剩余能量影响规律.

1 聚能射流侵彻理论

1.1 侵彻深度计算模型

本文中聚能射流的侵彻深度计算基于ALLISON 等[21]提出的准定常侵彻理论，假设存在某一虚拟源，虚拟源上的各射流微元的速度假设为在空间上线性分布，如图1 所示.取射流头部虚拟源为坐标原点O，每一直线的斜率即为该射流微元的速度；S为虚拟源到靶板表面的距离；t0为射流头部从虚拟源运行到靶体表面的时间.图1 为射流侵彻靶板过程的分析图，其中横坐标t为时间，纵坐标P为侵彻深度.

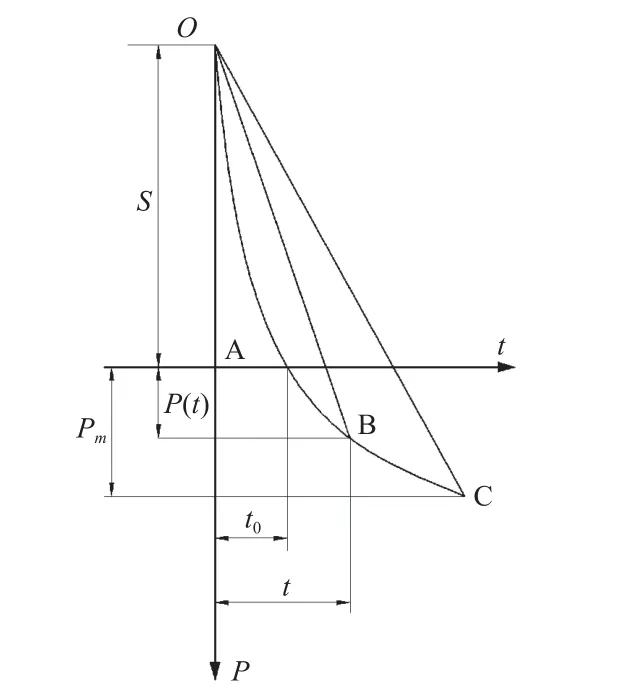
图1 非匀速射流侵彻分析图Fig.1 Model of jet penetration analysis

射流头部在A 点与靶体表面相遇并开始侵彻，ABC 线为侵彻深度随时间增加的曲线，该曲线上每一点的斜率即为该点的侵彻速度或碰撞点速度.

根据流体动力学理论，在侵彻过程中碰撞点两侧的静压与动压之和必须相等.不考虑弹靶强度，根据伯努利方程有

式中：ρj、ρt分别为射流和靶板密度；vj、u分别为射流速度和侵彻速度.

可得到侵彻深度随射流尾部速度变化的函数

经过适当的代换可得到射流侵彻深度随时间变化的表达式

1.2 射流拉伸运动及形状函数表征

由于聚能射流具有头尾部速度差异较大的特性，其在飞行过程中的拉伸效应不可忽略，为描述聚能射流在飞行过程中的形状变化，本节拟建立聚能射流拉伸运动中的形状变化表征函数.假设在运动过程中射流微元速度不发生变化且认为射流均匀地拉长，根据PER 准定常理论[22]可知射流微元速度沿射流长度方向呈线性分布，假设任一已知射流形态的时刻tm及射流飞行过程中任意时刻t，以射流由tm时刻运动至t时刻的过程作为考察对象，假设射流某点速度为v， 以射流尾部作为坐标原点，对应速度为v的射流微元位置坐标为x，tm时刻对应的射流形状函数为r=fm(x)，射流在tm时刻的长度为l(tm)，运动至t时刻时，其对应的射流形状函数为r=ft(x)，射流长度为l(t).根据假设，射流在着靶前的全过程中，头尾部速度保持不变，头部速度为v0，尾部速度为vt.图2 为射流的运动过程示意图.

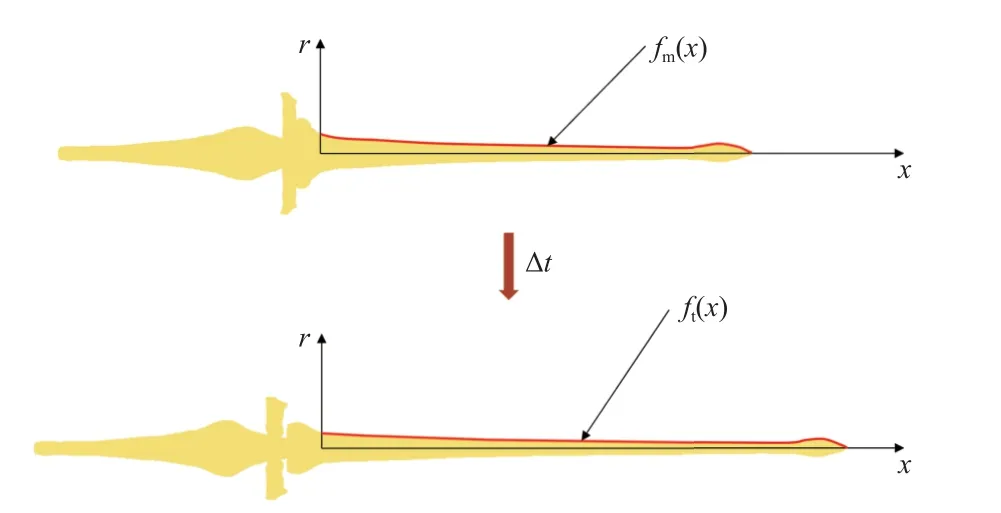
图2 射流拉伸过程各参量示意图Fig.2 Model of jet movement and stretching

根据以上假设且由几何关系可得到微元速度为v对应的微元位置xv表达式

假设射流微元在拉伸过程中的拉伸速度为vs，且根据射流微元的质量、密度均保持不变等假设，根据质量守恒定律建立两时刻下射流微元体积恒定的等量关系

式中：rm、rt分别为在tm时刻与t时刻下同一速度v处的射流半径.

对式(5)进行化简可得式(6).由式(6)可知，在射流拉伸过程中射流微元的半径随着时间t的增加以比例系数n在逐渐减小.

则射流由tm时刻运动至t时刻其形状函数可表示为

由此可得出射流在任一时刻t对应速度为v处的射流半径r的表达式

1.3 侵彻孔径计算模型

基于王静等[7]建立的聚能射流侵彻孔径计算模型，假设射流与靶板接触过程中，除了轴向的侵彻作用也会对靶板产生径向的扩孔作用.随着射流与靶板的相互作用，射流与靶板接触区域会产生较大的应力，其头部近似为一蘑菇头状，且靶板内壁由于射流径向的挤压作用会获得一定的动能.由于惯性的作用，靶板材料会产生进一步的扩张，形成了终态的侵彻孔径形貌.

侵彻孔径的计算依然承袭射流准定常侵彻理论假设条件，射流考虑为无黏性不可压缩流体，靶板材料均匀且不考虑侵彻过程中的可压缩性；弹靶交汇处射流速度为vj，侵彻速度为u，其中β为射流中心流线切线方向与对称轴z轴正方向之间的夹角，dβ为β的微分变量，r为射流中心流线上点距z轴的径向距离，将射流头部分为流动区(β=90°～180°)和驻定区(β=0°～90°)，在驻定区，不考虑靶板强度，靶板对射流的动压力为1/2ρTu2.其侵彻理论模型如图3 所示.

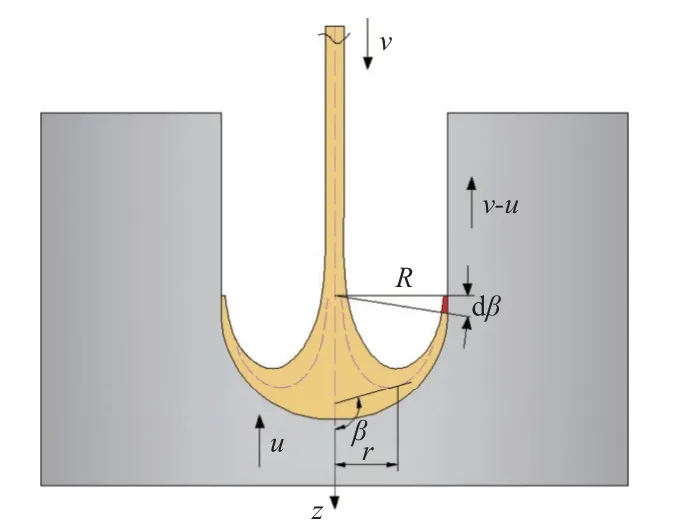
图3 侵彻孔径理论模型示意图Fig.3 Model of jet penetration hole calculation

基于定常不可压缩流体的若干性质及质量守恒方程，结合SZENDREI 等[4]对微元体在Δt时间内的动量变化关系

式中：pC为聚能射流对靶板孔道内壁产生的压力：σ为靶体阻力；UC为聚能射流的扩孔速度.

基于HELD 等[5]对于孔道内壁膨胀速度UC等于射流轴向侵彻速度的假设，利用第一节关于射流速度、侵彻深度及时间的等量关系，经过一定的代换即可得到最终孔径大小rf随侵彻深度变化的函数关系

式中：r(v)为聚能射流的形状函数；P为侵彻深度.

1.4 侵彻后效参量计算模型

在剩余头部参量计算方面，本文将承袭HELD所提出的v2d准则来其进行考量.为研究不同形状特性聚能射流对有限厚靶板的侵彻剩余参量变化，基于前述聚能射流侵彻计算模型与射流拉伸运动及形状表征，建立了聚能射流侵彻有限厚靶板的剩余头部参量v2d及剩余动能的计算模型，其示意图如图4所示.该计算模型基本假设如下：

①在射流自由飞行过程中射流的头尾部速度保持不变，射流各微元速度呈线性分布；

②射流在自由飞行和侵彻靶板过程中保持连续；

③射流和靶板材料均为不可压缩介质，忽略靶板强度对侵彻过程的影响；

④忽略射流对有限厚靶板侵彻开始阶段及结束过程中的射流损失，并假设上述过程为连续的过程.近似的认为，若某聚能射流对半无限金属靶板的侵彻深度为T，则该聚能射流侵彻厚度为T的有限厚金属靶板时，聚能射流完全耗尽的同时靶板恰好完全贯穿.

假设聚能射流贯穿有限厚靶板后其剩余射流头部刚好到达靶板背部的时间为tr，则由前文中各计算模型可得到其剩余射流头部速度vr及直径d，进而可求得聚能射流侵彻有限厚靶板的剩余头部参量v2d的表达式

式中T为有限厚靶板的厚度.

根据前文假设的射流速度关系与射流半径关系对剩余射流的每一射流微元进行定积分计算即可得到聚能射流侵彻有限厚靶板剩余动能的表达式

式中Er为聚能射流侵彻有限厚靶板剩余动能.

2 聚能射流X 光及静破甲试验

2.1 弹靶情况与试验布置

试验弹体采用Φ50 mm 口径聚能装药，聚能装药采用带罩压药的方式制备完成，炸药采用压装JH-2(8701)炸药，装药高度为59 mm，装药密度为1.71 g/cm3，装药质量约106 g；药型罩材料为紫铜，口径为48.8 mm，药型罩锥角50°，药型罩高度为47.1 mm.聚能装药结构及装药与药型罩实物图如图5 所示.

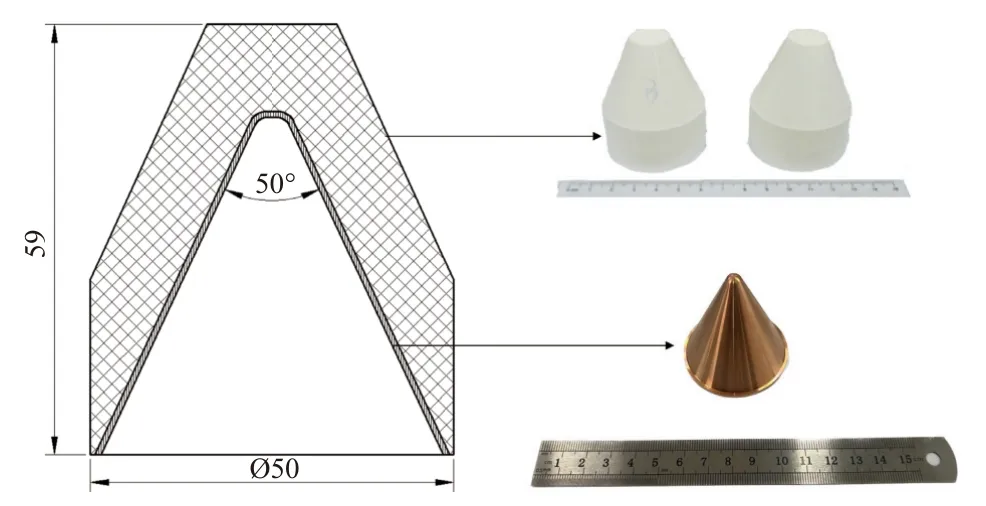
图5 聚能装药及药型罩结构图Fig.5 Structure of shaped charge

X 光摄影试验采用两台脉冲X 光机组合拍摄脉冲X 光摄影试验布局如图6(b)所示，X 射线管A 和X 射线管B 呈45°汇交.聚能装药垂直放置于两台X射线管的汇交区域.试验过程中，设置X 射线管A 先工作，X 射线管B 后工作，获得射流在不同时刻的X光照片.静破甲试验布置如图6(a)所示，包括雷管、雷管座、传爆药、聚能装药、炸高筒以及靶板.炸高为150 mm，炸高筒由尼龙制成; 靶板材料为45 号钢.试验前，标记靶板与聚能装药的相对位置，其中靶板的标记线对应截面的下底中点.

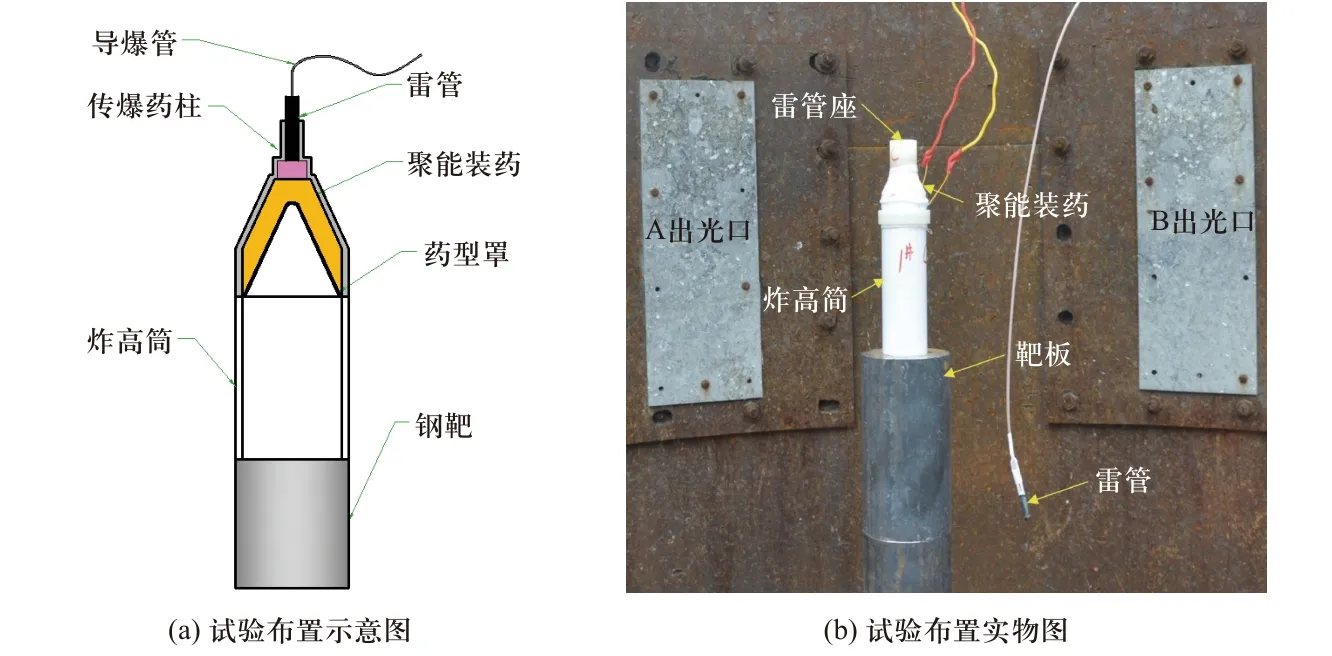
图6 试验现场布置图Fig.6 Experiment setup

2.2 试验结果及分析

2.2.1 射流成型X 光结果及分析

为尽量减少单次试验带来的不确定性，本次试验在相同工况下进行两发重复试验.试验结束后对两发试验的X 光影像与靶板穿孔形状进行了处理.图7 为两发试验获取到的在不同时刻下的射流X 光影像.由X 光图像可知，两发试验射流成型均良好且准直.其中，第一发试验X 光出光时间为A 出光口19.76 μs，B 出光口22.68 μs.第二发试验X 光出光时间为A 出光口17.42 μs，B 出光口20.78 μs.对两发X光射流影像进行了数据处理，分别得出了两发试验射流头尾部速度、较后时刻射流头部直径及射流长度，详细数据见表1.

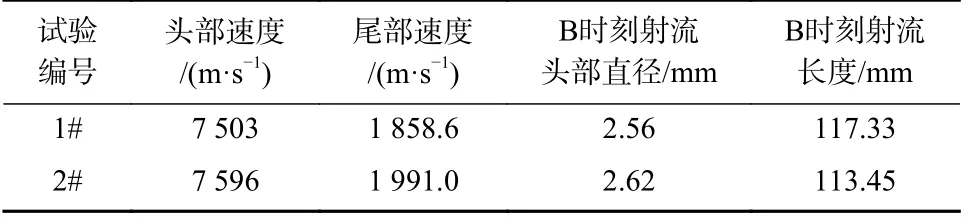
表1 射流成型参数表Tab.1 Parameters of jet formation

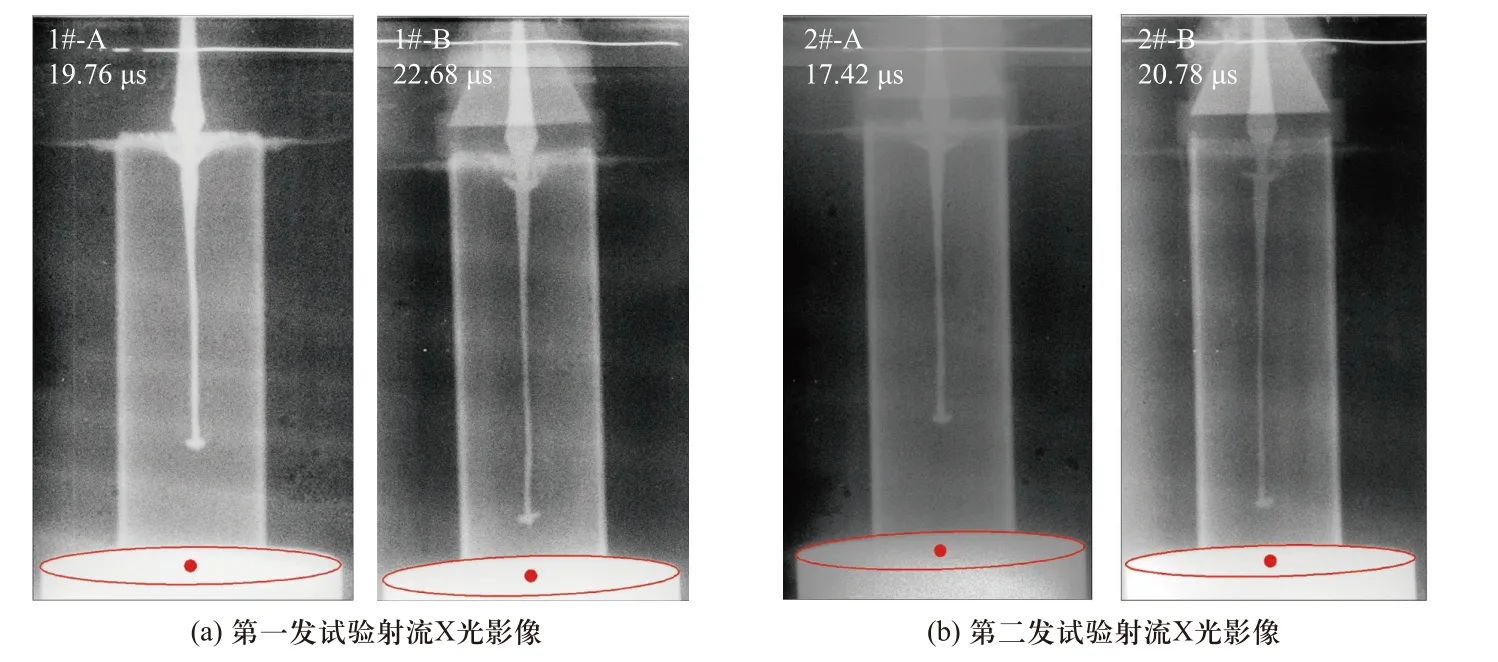
图7 射流X 光影像Fig.7 X-ray images of jet formation

在某一时刻下，射流的外轮廓可看作一条射流直径随射流微元位置坐标变化的函数曲线，其定义域处在射流头部与尾部之间.本文采用了三种常见的函数关系分别对射流的形状进行描述以获得不同形状函数工况下的侵彻孔型情况，其三种函数关系分别为常函数、一次函数及二次函数，其函数关系由表2 给出.通过对试验中获取到的射流源X 光影像进行等效，拟合得到了三种形状函数的函数图像如图8 所示.

表2 三种形状函数及其表达式Tab.2 Expressions of three jet shapes

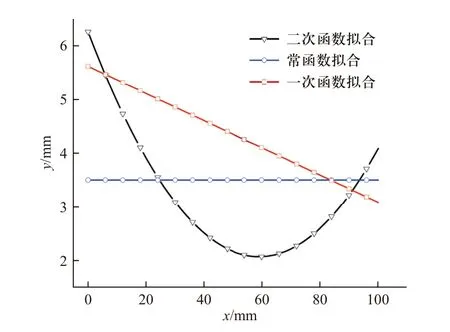
图8 三种形状函数图像Fig.8 Curves of three jet shape

在射流的飞行过程中由于头尾部存在速度差异，射流在不断地拉伸，为了保证形状函数在拉伸过程中能够对射流形状进行较为准确的描述，通过与试验中X 光两个时刻下的射流影像进行对比，对其拉伸过程中射流半径变化的计算模型可靠性进行检验.

图9(a)中给出了在装药起爆19.76 μs 时刻射流各位置处的直径，并根据X 光数据对射流的三种形状函数进行了拟合得到了其形状函数曲线，由图可知二次函数模型能够较为贴合地对聚能射流的形状进行描述；图9(b)给出了在聚能装药起爆后22.68 μs时刻的射流形状参数散点图，通过本文第一节建立的射流拉伸过程中形状变化公式计算得出三种形状函数在该时刻下的函数图像并与试验数据进行对比，结果表明本文所建立的射流直径变化计算模型在射流拉伸过程中具有较好的描述性.

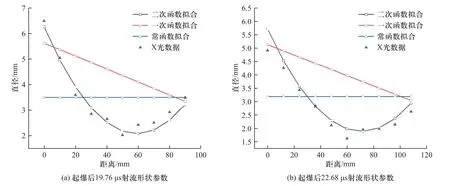
图9 不同时刻下射流实际形状参数与形状函数对比Fig.9 Comparison of X-ray experiment and shape functions of jet at two moments

2.2.2 静破甲试验结果及分析

试验结束后对靶板进行了回收，利用线切割技术将靶板沿射流侵彻孔洞圆心将靶板切开，并描绘射流孔道形状，如图10 所示.通过测量获取了两发试验的射流侵彻深度及不同侵彻深度处射流侵彻孔径.第一发试验中射流对靶板的侵彻深度为216.43 mm，第二发试验中射流对靶板的侵彻深度为232.12 mm，两者相差6.7%，重复性较好.将射流孔道各个深度处的侵彻孔径进行了统计，并绘制了两发试验射流侵彻孔径大小随侵彻深度变化的散点图，如图11 所示.

图10 射流侵彻靶板毁伤情况Fig.10 Targets penetrated at the standoff of 150 mm

图11 射流侵彻孔径大小随侵彻深度变化散点图Fig.11 Curves of hole diameter varying with penetration depth

根据本文所建立的侵彻计算模型，提取试验中X光试验结果中的射流影像，获取了射流成型的各项基本参数，包括头尾部速度以及射流在X 光出光时刻的头部半径.根据本文建立的理论模型，需进一步获取理论计算所需要的初始参量.其中，弹靶密度、射流头尾部速度可由试验结果直接获取，剩余所需参数中，射流着靶时刻头部半径及虚拟源与靶板表面的距离可根据X 光拍摄结果并结合假设条件计算得出，靶体阻力取值根据学者SZENDREI[11]开展的射流侵彻钢靶的试验结果拟合得到.其具体数值由表3 给出.

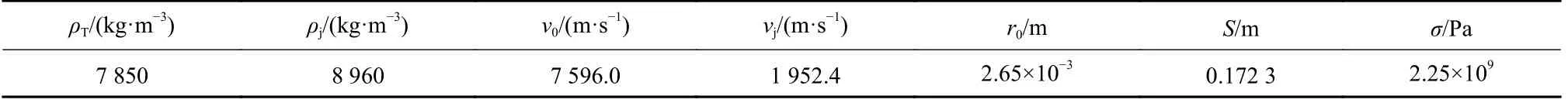
表3 理论计算各初始参量取值Tab.3 Value of each initial parameter

表中，ρT为靶板密度，ρj为射流密度，v0为射流头部速度，vj为射流尾部速度，r0为射流着靶时刻的头部半径，S为虚拟源点与靶板表面的距离，σ为靶体阻力.

根据上述射流基本参数，首先得到了该射流侵彻钢靶时侵彻深度的时程曲线，并得到了最终的侵彻深度计算结果为225.3 mm，并将侵彻深度试验结果标记于曲线图中，如图12 所示.由计算结果与试验结果对比可知，计算误差较小，其上下跳动误差绝对值小于5%.获得了计算侵彻深度值后，接着对该聚能射流的侵彻孔径进行理论计算，由本文建立的侵彻孔径理论计算模型可知，除描述射流形状的形状函数外，其他所需输入量均为已知参数或可从试验结果中获取，如表3 所示.针对表2 给出的三种形状函数，开展了该射流源对半无限钢靶的侵彻孔径计算，图13 为各情况下的计算结果与试验结果对比.

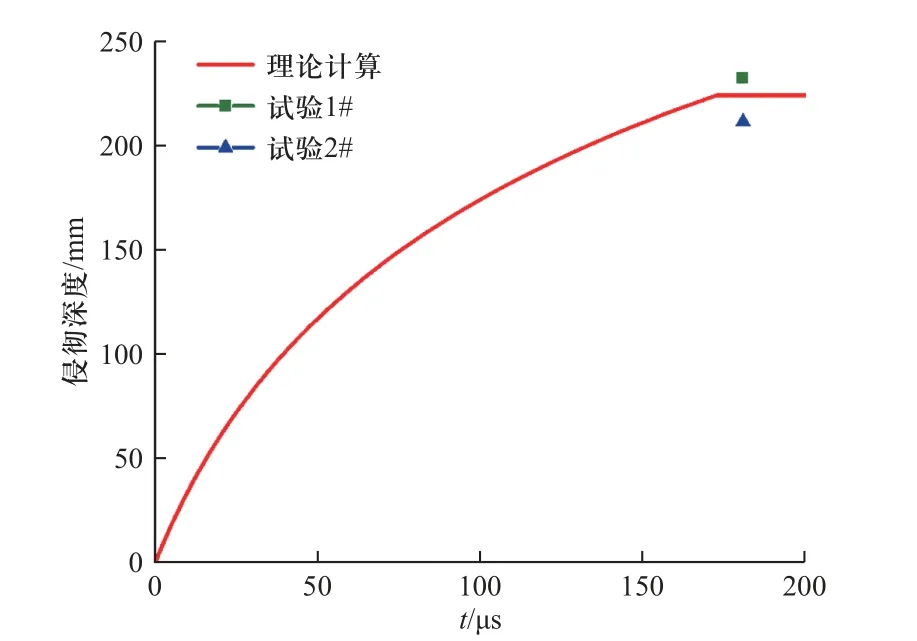
图12 理论计算侵彻深度时程曲线与试验结果对比Fig.12 Curve of penetration depth varying with time

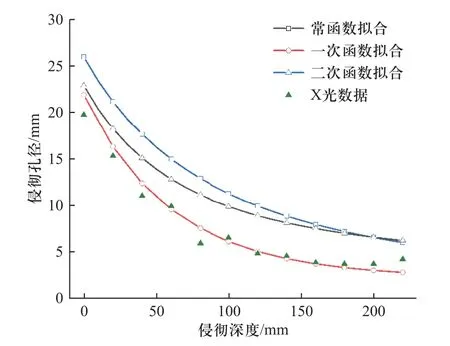
图13 三种形状函数计算结果与试验对比Fig.13 Curve of penetration hole by theoretical calculation

由计算结果可知，三种形状函数中采用二次函数表征方式的计算结果与试验中得到的侵彻孔型最为接近且几乎重合，常函数与一次函数表征方式下，侵彻孔型的计算结果均与试验结果存在较大误差.本小节的计算结果表明，在选取合适的聚能射流形状表征函数时，本文采用的聚能射流侵彻计算模型具有较好的预测性；进一步说明，聚能射流入靶前的形状分布对于其对靶板的侵彻形貌有显著的影响.

2.3 考虑形状分布特性的聚能射流侵彻靶板剩余参量规律研究

不同形状特性聚能射流侵彻有限厚靶板靶后v2d计算方法如下：基于前述给出的三种射流形态参数，开展了三种不同形状特性聚能射流对有限厚靶板侵彻后效参量的理论计算，得到了三种形状特性射流在不同有限厚靶板厚度条件下靶后参量v2d随炸高的变化曲线，如图14 所示.图14(a)～(c)给出了形状分别为二次函数、一次函数及常函数的射流在不同靶板厚度下靶后参量随炸高的变化曲线.其中，对炸高进行了量纲一处理，其单位为聚能装药口径D0.

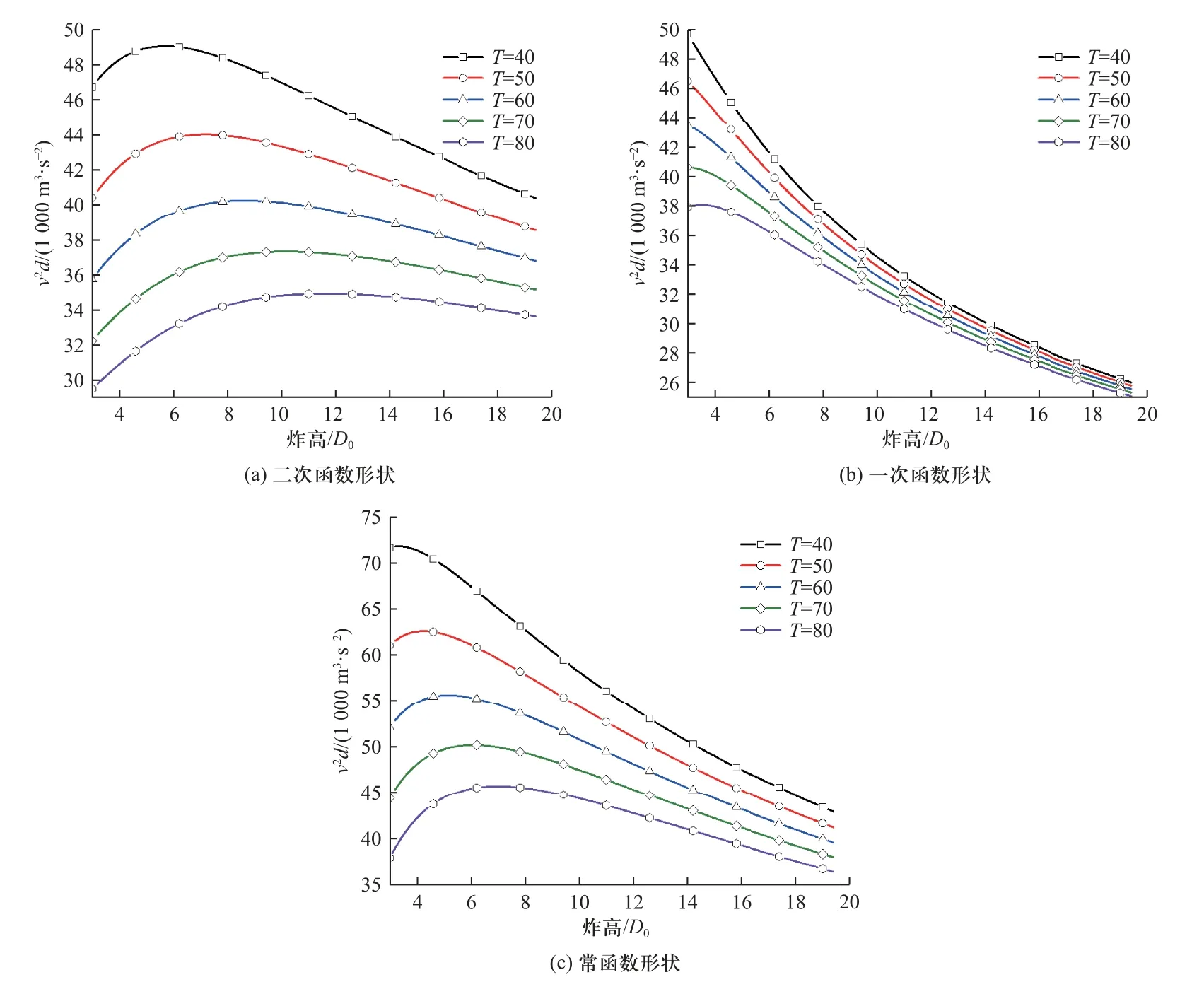
图14 三种形状射流在不同炸高及不同有限厚靶板厚度条件下的靶后参量计算结果Fig.14 Curves of v2d varying with standoff at three jet shapes

由图14 可知，三种形状特性的射流在不同靶板厚度条件下，其剩余头部参量大小均随着靶板厚度的增大呈现逐渐减小的趋势.当靶板厚度一定时，形状为二次函数和常函数的聚能射流其剩余头部参量随着炸高的增加呈现先增大后减小的趋势，二次函数形状聚能射流在6～10 倍装药口径炸高处取得靶后参量最大值，常函数形状聚能射流在3～7 倍装药口径炸高处取得.随着靶板厚度的增大，其最大靶后参量炸高数逐渐增大.而形状为一次函数的聚能射流，在靶板厚度小于80 mm 的情况下，其剩余射流的头部参量随着炸高的增大呈现单调递减的趋势，当靶板厚度大于80 mm 时，其靶后剩余头部参量的变化逐渐呈现先增大后减小的趋势.

为研究在靶板厚度不变的情况下三种不同形状特性的聚能射流侵彻有限厚靶板靶后参量的变化规律及异同，以靶板厚度分别为50、60 mm 工况为例，提取了三种不同形状特性的聚能射流剩余头部参量计算结果，如图15 所示.

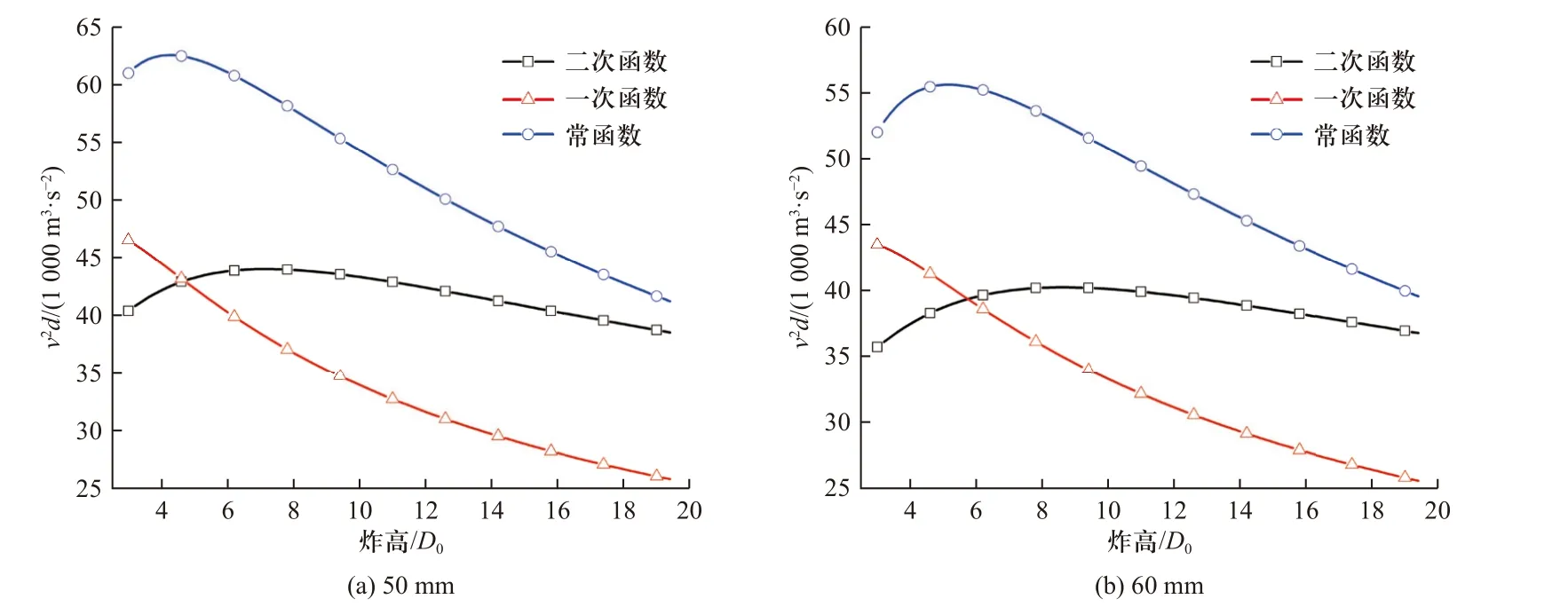
图15 同一有限厚靶板厚度下三种形状射流剩余头部参量随炸高变化曲线Fig.15 The curves of v2d varying with standoff at same thickness target

由图15 可知，在靶板厚度一定的情况下，形状为常函数的聚能射流其靶后参量在3～20 倍装药口径炸高位置均优于形状为二次函数与一次函数的聚能射流；在三倍装药口径炸高处，形状为一次函数的聚能射流剩余头部参量要大于形状为二次函数的聚能射流，但随着炸高的增大，形状为二次函数的聚能射流的剩余头部参量逐渐高于形状为一次函数的射流，两曲线相遇处的炸高大小随着靶板厚度的增大逐渐增大.由计算结果可知，三种形状的聚能射流剩余头部参量随炸高增大的减小速度并不相当，其中，形状为二次函数的聚能射流剩余头部参量随着炸高增大的减小速度最为缓慢，受炸高影响较小；形状为常函数的聚能射流剩余头部参量在到达峰值后的下降速度与形状为一次函数的聚能射流下降速度相当.

2.4 不同形状特性聚能射流侵彻有限厚靶板剩余动能计算

基于前文给出的三种射流形态参数，开展了三种不同形状特性聚能射流对有限厚靶板侵彻剩余射流动能的理论计算，得到了三种形状射流在不同有限厚靶板厚度条件下剩余射流动能随炸高的变化曲线，如图16 所示.图16(a)～(c)给出了形状分别为二次函数、一次函数及常函数的射流在不同靶板厚度下剩余射流动能随炸高的变化曲线.

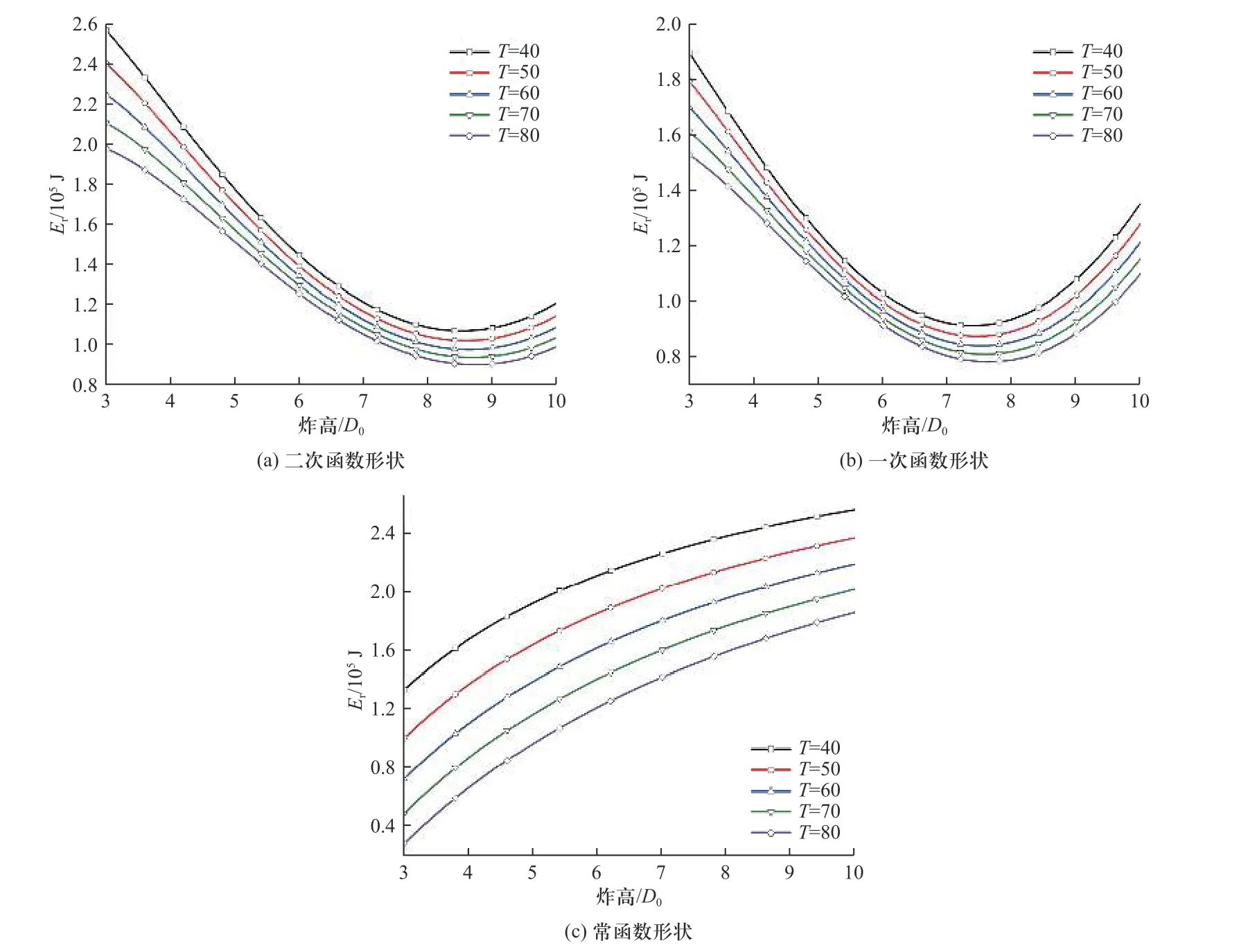
图16 三种形状射流在不同炸高及不同有限厚靶板厚度下的射流剩余动能计算结果Fig.16 Curves of Er varying with standoff at three jet shapes

由图16 可知，在靶板厚度一定时，形状为常函数的聚能射流剩余能量随着炸高的增大而增大，增大的速度在逐渐降低，其剩余射流能量值逐渐逼近于射流总能量；形状为二次函数和一次函数的聚能射流其剩余射流能量随着炸高的增加呈现先减小后增大的趋势，且其剩余能量最小取值处位于7～9 倍装药口径炸高之间，二次函数形状射流取得最小剩余能量位置要滞后于一次函数形状射流，在剩余射流能量取得最小值后，又呈现随炸高逐渐增大的趋势.在炸高一定的情况下，由于靶板厚度的增大消耗的射流能量逐渐增加，三种形状的聚能射流其侵彻有限厚靶板的射流剩余能量随着靶板厚度的增大逐渐减小.

为研究三种不同形状特性的聚能射流侵彻有限厚靶板剩余射流能量的变化规律及异同，分别提取了两种有限厚靶板厚度下，三种不同形状特性的聚能射流侵彻有限厚靶板剩余动能的计算结果，如图17 所示，图17(a)、(b)分别为三种形状特性聚能射流在靶板厚度为50 mm 与60 mm 工况下靶后剩余射流动能变化规律.

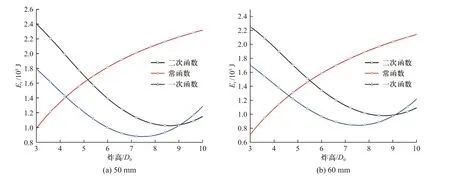
图17 同一有限厚靶板厚度下三种形状射流靶后剩余动能随炸高变化曲线Fig.17 Curves of Er varying with standoff at same thickness target

由以上计算结果可知，在三倍装药口径炸高条件下，三种形状聚能射流按照剩余射流能量从高到低的顺序排列依次为二次函数＞一次函数＞常函数，这是由于形状为常函数的聚能射流其能量分布均匀，而二次函数和一次函数形状的聚能射流大部分能量分布于聚能射流尾部，且二次函数形状的射流相较于一次函数形状的射流其能量分布更加集中于射流尾部，炸高较低情况下消耗的射流占总射流的百分比较大，所以导致了该情况的出现.随着炸高高度逐渐增大，常函数形状的聚能射流其剩余射流能量逐渐超越一次函数与二次函数形状的射流，且常函数形状射流剩余能量曲线与一次函数、二次函数形状射流剩余能量曲线相交的位置随着靶板厚度的增大而逐渐后移，说明随着有限厚靶板厚度的增大常函数形状的聚能射流剩余能量在逐渐接近一次函数与二次函数形状的聚能射流.

3 结 论

本文开展了50 mm 聚能射流源成型X 光及侵彻半无限45 钢靶板试验，建立了考虑聚能射流形状函数的侵彻计算模型，通过试验数据与计算结果的对比，验证了计算模型的可靠性.在此基础上，系统分析了聚能射流形状、炸高及有限厚靶板厚度对聚能射流侵彻有限厚靶板靶后头部v2d及剩余射流动能的影响规律.主要结论如下：

①通过开展常函数、一次函数及二次函数形状的聚能射流侵彻孔型与后效参数理论计算发现，二次函数对聚能射流的形状表征最为贴合，且聚能射流的形状对于其侵彻孔型及侵彻后效有着显著的影响.

②在剩余射流头部参量v2d方面，随着炸高不断地增大，形状为二次函数和常函数的聚能射流剩余头部参量呈现先增大后减小的趋势，形状为一次函数的聚能射流剩余头部参量呈现逐渐减小的趋势.在三种形状的聚能射流中，常函数形状的射流在各个条件下其靶后剩余射流头部参量均为最大.

③在剩余射流动能方面，随着炸高不断地增大，形状为二次函数和一次函数的聚能射流侵彻有限厚靶后剩余射流动能呈现先减小后增大的趋势，形状为常函数的聚能射流侵彻有限厚靶剩余动能呈现逐渐增大的趋势.