传爆药超压峰值理论计算公式优化研究

余炜，王健，刘通有，孙其然

（1.南京理工大学 能源与动力学院，江苏，南京 210094；2.航空工业洪都650 飞机设计研究所，江西，南昌 330000）

对于炸药爆炸反应，冲击波超压是评价其威力的重要参数.许多学者对爆炸冲击波的超压峰值分布规律进行了研究，总结出了一些用以估算冲击波超压峰值的经验公式与半经验公式[1-5]，其中Mills公式[5]、Henrych 公式[2]、Sadovskyi[3]公式被广泛接受及应用，但这些经典经验公式由于缺少大量试验结果修正，其计算结果与实测结果存在较大偏差，且对计算非理想炸药的爆炸威力存在局限性，无法用于实际情况下炸药爆炸威力的评估.为了提高经验公式的准确性与适用性，国内外研究人员对这些经验公式模型进行了进一步优化及参数拟合，如仲倩等[6]将试验结果与多种经验公式计算结果进行比较，通过爆炸相似律及最小二乘法对TNT 爆炸产生的超压峰值进行了拟合，得出了更为精确的TNT 超压峰值计算经验公式，但是该公式对非理想炸药的评估效果没有进行论证与相应计算； XUE 等[7]借助数值模拟及爆炸相似律，提出了超压预测数学模型，该模型能对爆炸过程的冲击波超压全过程波形进行快速估算，包括超压峰值、正压区和负压区，但该模型未进行试验数据比对验证，能否用于战斗部威力评估仍需进一步验证；BAJIĆ等[8]对塑性炸药PPE-01 爆炸超压峰值进行了试验测试，并与多种经验公式比对，进行了全面的误差评估，发现Sadovskyi 公式[3]可以较好地描述PPE-01 的超压峰值，但其未进一步进行参数拟合，提出更能准确估算该炸药超压峰值的经验公式.

由于传爆药承担着传递爆轰的任务，既需要适合的冲击波感度，也需要形成稳定的爆轰波，故研究其冲击波超压特性具有重要意义.国内外对于传爆药超压进行了许多研究，如PEUKER 等[9]利用数值仿真方法分析了粒度及气体含量对RDX 基传爆药爆炸和超压增强现象的影响，王作山等[10]通过试验研究了装药直径对传爆药爆炸超压的影响.但这些研究成果主要集中讨论了外部约束条件以及内部化学成分对传爆药超压峰值影响的定性规律，并没有给出能准确评估传爆药爆炸超压的经验计算公式.

为进一步研究传爆药的爆炸场特性及威力，做到能以较小的误差估算传爆药爆炸产生的冲击波超压峰值，本文制备了不同密度的半球型及圆柱型钝化RDX 传爆药及TATB 传爆药，并设计了多组空中爆炸试验，结合数值仿真及理论计算进行分析，得到了装药类型、密度、形状等因素对传爆药冲击波超压峰值的影响，将试验结果与现有经验公式的计算结果进行比对，并借助爆炸相似理论对两种传爆药的超压峰值经验公式模型进行参数拟合，得到更能准确估算不同装药形状的钝化RDX 传爆药及TATB传爆药超压峰值的特定经验公式.

1 传爆药空中爆炸试验

1.1 试验准备与布置

由参考文献可知，当爆高H（炸药离地高度，单位为m）满足以下条件，可认为该爆炸属于无限空中爆炸[11]：

将传爆药的等效TNT 装药量代入式(1)，设置统一爆高为1.4 m.

将两种传爆药粉末压制成密度不同的半球型及圆柱型，圆柱型传爆药直径为28 mm，高度为36 mm，半球型传爆药直径为52 mm，弧面中心处留有雷管孔.使用尼龙壳将传爆药与雷管紧密固定，将测试炸药吊置在离地1.4 m 的空中，3 个传感器成环形间隔布置，与炸药爆心的距离分别为1 m，1.5 m，2 m，高度与爆心平齐，距爆心10 m 处布置高速摄像机及红外热成像仪，试验布置如图1 所示.

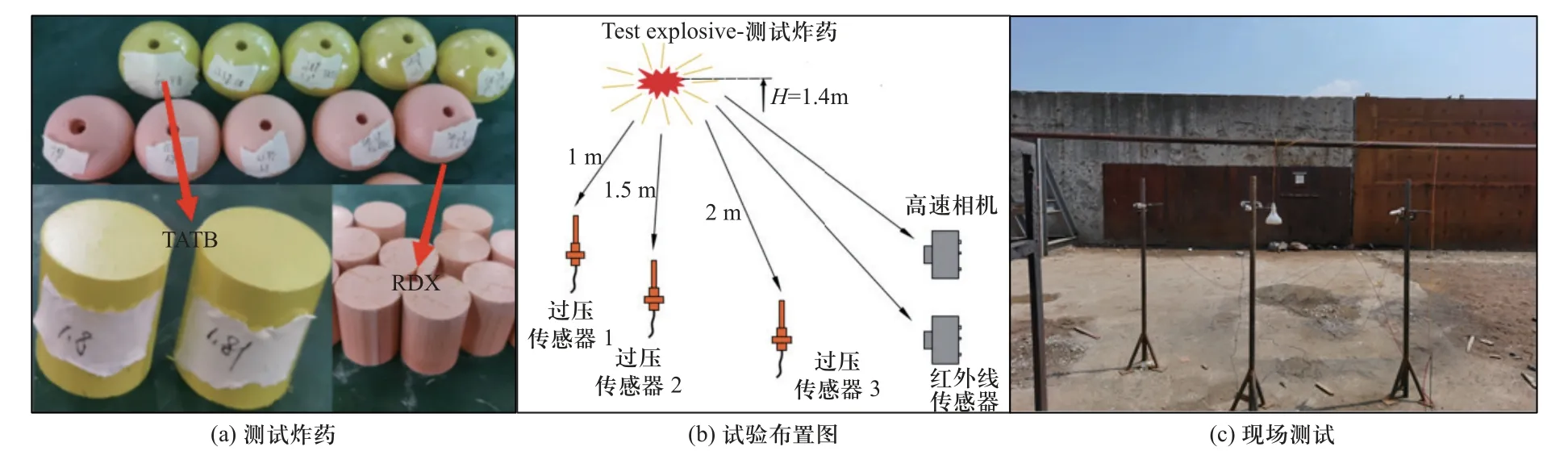
图1 试验布置Fig.1 Layout of test

1.2 试验内容

测量不同密度及形状的两类传爆药爆炸情况，试验具体方案如表1 所示.

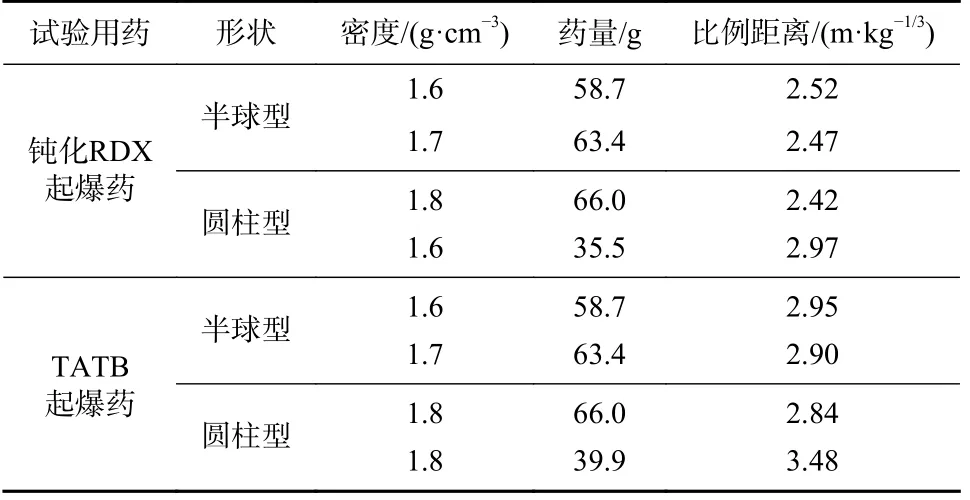
表1 试验方案Tab.1 Test scheme

共进行8 组起爆试验，每组试验重复3 次，试验结果剔除明显误差后取平均值.

1.3 试验结果

超压传感器在各测量距离得到不同工况下传爆药爆炸冲击波波形，部分结果如图2 所示.

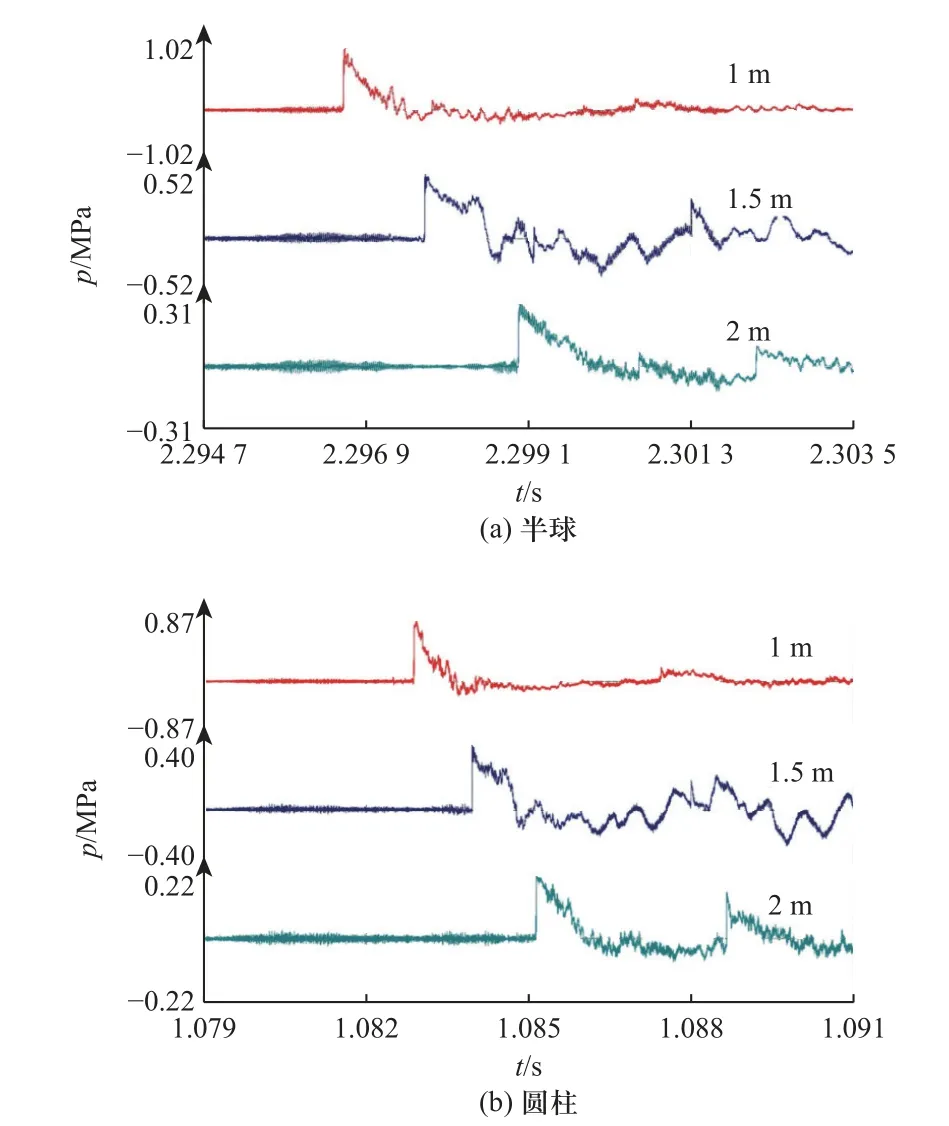
图2 不同形状RDX 传爆药实测超压波形图( ρ = 1.60 g/cm3)Fig.2 The measured overpressure waveform diagram of RDX booster explosive with different shapes ( ρ = 1.60 g/cm3)

受试验中震动冲击、高温等测试环境因素的影响，传感器捕获的冲击波信号会叠加大量环境噪声.为减小噪声的影响，采用小波滤波的方式对传感器输出数据进行去噪处理，即先对被污染的信号进行小波变换，然后通过调试小波系数去除其中的噪声，最后进行小波逆变换，得到去噪后的冲击波信号.将去噪处理后取得的超压峰值数据列于表2.

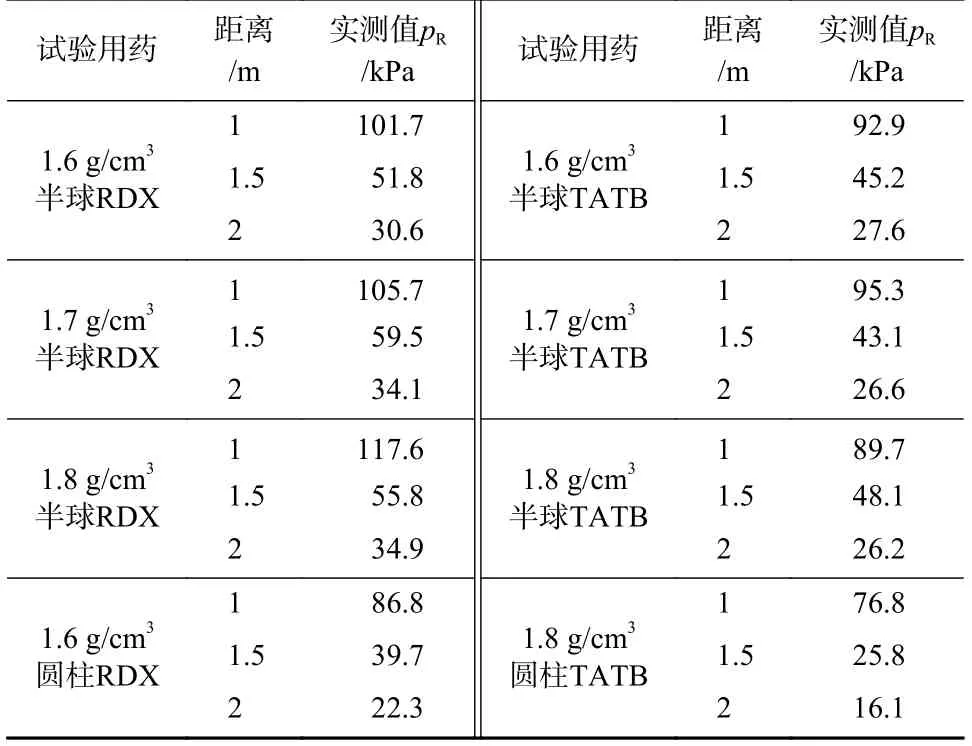
表2 试验测试超压数据Tab.2 Test overpressure data

2 数值仿真研究

2.1 超压峰值数值仿真分析

运用ANSYS/AUTODYN 软件对空中爆炸过程进行数值计算，将模拟值与试验值进行对比研究.由于试验中最大测量距离为2 m，爆炸空气域较大，因此使用二维轴对称模型与映射方法求解，即先在小空气域中完成传爆药起爆模拟，待冲击波到达小空气域边界处时，映射到大空气域中继续传播，这样既可保证计算精确性，又能有效加快求解速度.通过初步试算，考虑计算速度和精度的条件下，最终设置小空气域尺寸(长×宽)为60 mm×90 mm，网格尺寸为0.4 mm，并在炸药附近对网格进行加密，加密网格尺寸为0.2 mm.大空气域尺寸(长×宽)为1 000 mm×2 100 mm，网格尺寸为4 mm.设置无反射边界，该边界条件适用于模拟无限空域，有限元模型如图3所示.

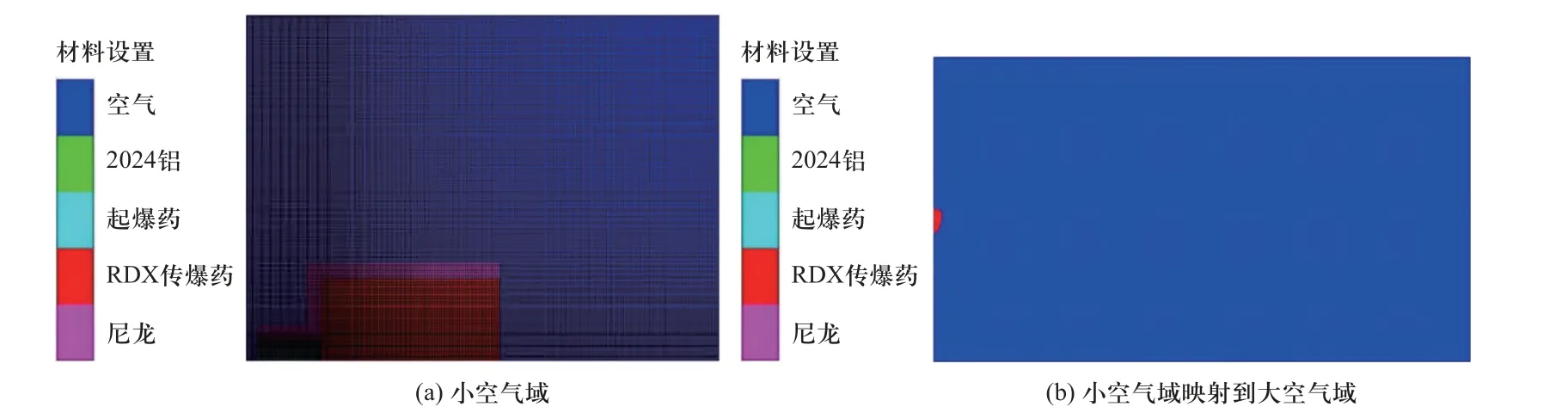
图3 有限元计算模型Fig.3 Finite element calculation model

铝合金雷管壳采用J-C 强度模型及Gruneisen 状态方程；尼龙壳体材料的状态方程为Shock 方程，强度模型使用von Mises 准则[12].起爆药及传爆药均采用JWL 状态方程，其中钝化RDX 及TATB 传爆药的爆炸反应均采用三项式点火增长模型描述[13]，根据相关文献研究[14]及试验结果对JWL 状态方程以及点火增长模型参数进行调整，具体参数见表3；将超压模拟值及其与试验值的相对误差列于表4.

表3 传爆药状态方程参数Tab.3 State equation parameters of booster explosive

表4 超压峰值模拟值比对分析表Tab.4 Overpressure peak simulation value comparison analysis table

将密度为1.7 g/cm3的两类传爆药在不同测点处的冲击波形绘制于图4.

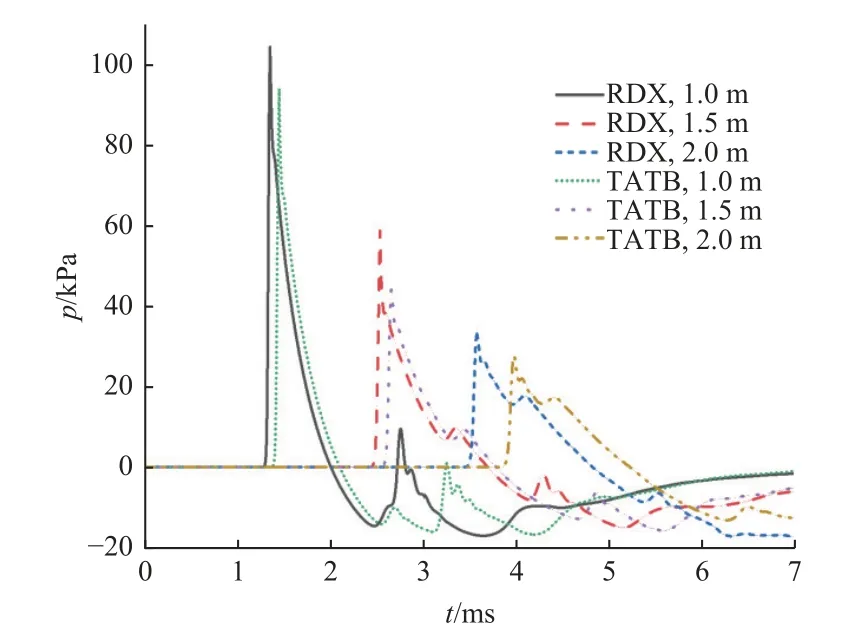
图4 传爆药不同测点处的冲击波形( ρ = 1.70 g/cm3)Fig.4 The measured overpressure of RDX booster explosive with different shapes ( ρ = 1.70 g/cm3)

结合表2、图4 可知，考虑高密度情况下TATB 传爆药可能存在爆炸不完全情况，排除密度为1.8 g/cm3的半球型及圆柱型TATB 传爆药超压模拟数据，两类传爆药在各测量点处模拟超压峰值与实测值误差较小，最大相对误差为6.10%；模拟传爆药爆炸的冲击波波形均为典型的空中爆炸冲击波时程曲线，符合冲击波超压传播规律.可以判定，使用的数值仿真算法可以较好地描述传爆药空中爆炸过程，但数值仿真方法需要的时间较长、工作量较大，需要补充经验公式理论估算方法作为快速评估的手段.

2.2 装药密度对超压峰值的影响

在装药形状和体积不变的情况下，装药密度增大一方面会提高炸药的整体装药量，另一方面会使得炸药间孔隙率降低，热点增长困难，从而使起爆难度增大[14-15].两类因素都会对炸药爆炸后产生的空气冲击波造成较大影响.选取不同密度的两类半球型传爆药在爆距为1 m 处的超压试验值与模拟值绘制超压-密度曲线，如图5 所示.

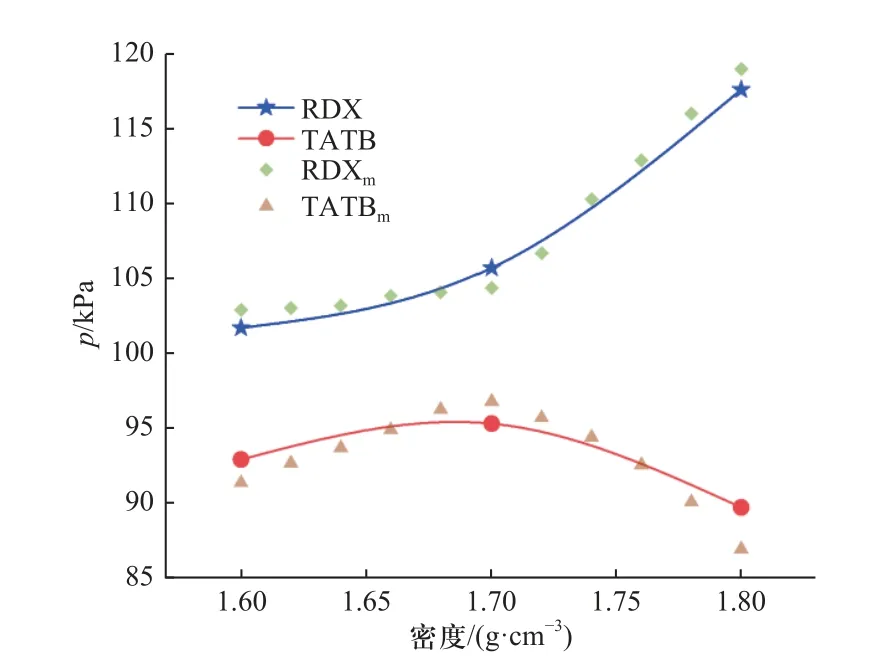
图5 半球型炸药在爆距1 m 处的超压-密度曲线Fig.5 The overpressure-density curves of hemispherical explosives at the detonation distance of 1 m

由图5 可知，随装药密度增大，钝化RDX 传爆药的爆炸冲击波超压峰值也增大，而TATB 传爆药的超压峰值出现先增大后减小的现象，这不符合超压峰值随装药量增加而单调递增的规律[2].分析认为TATB 传爆药密度增加，降低了炸药的冲击感度，使得药量的增加不足以抵消炸药未完全反应所带来的能量释放损失.这会导致理论公式计算方法无法准确评估高密度TATB 传爆药的超压峰值的情况.

3 超压峰值经验公式计算方法研究

3.1 超压峰值经验公式计算

经过多年研究，对于爆炸超压峰值已能做到较为准确的估算.常用方法是由比例距离估算[2]，比例距离定义如下：

式中：R为测点与爆心间距离 ，m ;WTNT为等效TNT装药量 ，kg.

通过计算传爆药与TNT 的爆热比，得出两种传爆药的比例距离与爆距之间转换公式如下：

式中WRDX与WTATB分别为两种传爆药的装药质量，kg.

通过式(3)确定传爆药在不同药量及距离下的比例距离，得被试传爆药最小比例距离为2.42 m/kg1/3，最大比例距离为6.97 m/kg1/3.

基于被试药起爆特性，选择以下3 种传统经验公式以及两种优化后的经验公式对超压值进行计算,公式中超压值单位均为MPa.

MILLS[5]通过爆炸相似理论及数值模拟得到的TNT 炸药在空中爆炸时冲击波超压峰值经验公式：

SADOVSKYI[3]根据爆炸相似理论建立比较式，由试验确定系数，得到的高爆炸药超压峰值经验公式：

仲倩[6]由试验测得数据，借助爆炸相似律及最小二乘法对TNT 爆炸超压峰值拟合得到的公式：

王儒策[16]给出的球型装药爆炸超压峰值的经验计算公式：

为直观对比各公式计算结果,用对数坐标绘出冲击波超压-比例距离关系曲线，如图6 所示.

由爆炸相似律可知，超压峰值pRX与比例距离之间的关系可以被描述为以下指数方程[2]：

式中A、B、C、D、E为需要进行拟合的参数，根据两种传爆药的试验与数值模拟结果，以式(9)为基础，运用最小二乘法原理，分别对钝化RDX 传爆药和TATB 传爆药进行参数拟合.

钝化RDX 传爆药的拟合公式如下,计算超压峰值单位为MPa.

对于TATB 传爆药，由于密度过大会降低其冲击感度，使传爆药起爆后不能完全反应，故只对其密度在1.6 m/kg3、1.7 m/kg3的试验数据进行拟合，式中超压峰值单位为MPa.

3.2 超压计算值与试验值对比分析

为更直观地表示出经验公式计算值与试验值(pR)、模拟值(pm)之间的差异，绘出密度为1.60 g/cm3的两类半球型传爆药在不同爆炸距离处的超压峰值曲线，如图7 所示.

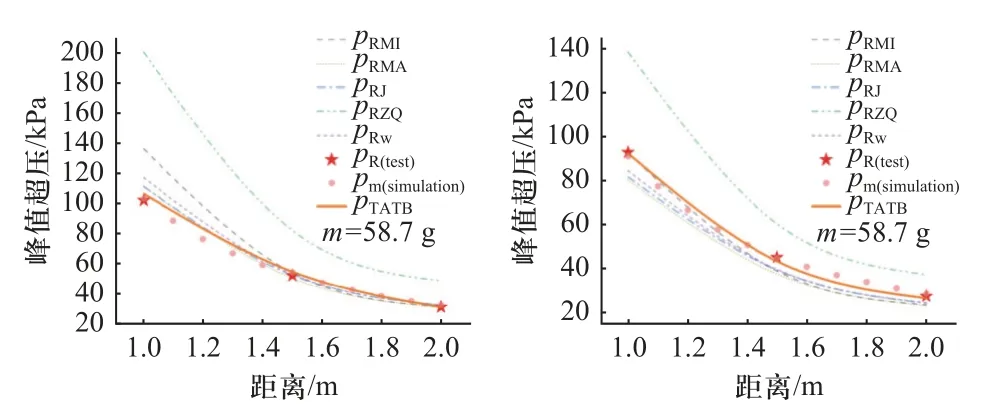
图7 两类半球型传爆药超压峰值曲线 ( ρ = 1.60 g/cm3)Fig.7 Peak overpressure curves of two hemispherical boosters ( ρ =1.60 g/cm3)

由图7 可知，两类半球型传爆药的试验超压峰值与经验公式(7)的计算值偏差较大，故不能使用此经验公式描述两类传爆药的冲击波超压特性.而对于其他经验公式，半球型TATB 传爆药实测值与各经验公式计算值偏差相对较小，而半球型钝化RDX传爆药在1 m 处的峰值超压实测值与经验公式(4)计算所得结果相差较大，误差为25.2% ，与其余经验公式计算值的误差在8.1%～12.9%.随着爆炸距离的增加，实测值与经验值的偏差迅速减小，在爆距为2 m 处，半球型钝化RDX 传爆药冲击波超压峰值实测值与计算值的最大误差为8.4%.爆炸近场误差较大的原因在于经验公式本身依靠前人试验数据进行拟合，但由于爆炸近场爆轰产物运动十分复杂，高压高热环境对测试装置的灵敏度和精度要求极高，收集的试验数据存在局限性.据上述对比，经验公式(6)可以较好地估算半球型钝化RDX 传爆药爆炸超压峰值，经验公式(4)则对半球型TATB 传爆药超压峰值估算更为准确.

而对于圆柱型装药而言，由于装药形状的不同，传爆药内部热点的形成及爆轰波的传递也会产生差异，其冲击波超压峰值也会发生改变.如图8 所示，经验公式(7)由于误差过大，仍不能用于描述圆柱型传爆药的超压峰值.对于圆柱型钝化RDX 传爆药而言，与半球型装药试验结果误差较大的式(4)误差明显减小，在1 m 距离处误差为5.3%，而式(8)计算值与试验结果的最大误差为3.7%，能较为准确地描述圆柱型钝化RDX 传爆药爆炸超压峰值；对于圆柱型TATB 传爆药，数值仿真结果与经验公式计算值误差均大于10%，考虑是因为圆柱型TATB 传爆药密度较大导致，由于不是理想爆炸情况，难以用理论算法评估.

图8 两类圆柱型传爆药超压峰值曲线( ρ = 1.60 g/cm3)Fig.8 Overpressure peak curves of two cylindrical boosters ( ρ =1.60 g/cm3)

通过上述对比分析可知，已有经验公式或是计算误差较大，或是不能全面地描述两类传爆药在不同装药形状下的超压峰值，均不适合作为评估钝化RDX 传爆药及TATB 传爆药的理论计算手段.

由图7、图8 可知，通过试验数据拟合优化后的经验公式与试验及数值模拟结果误差较小.由于经验公式的参数拟合过程基于爆炸相似律以及最小二乘法，是一个理想化的模拟过程，并不能保证所有试验数据都精确位于所拟合的公式曲线上，需要将经验公式的计算值与试验及数值计算结果进行对比分析，结果见表5.

表5 误差分析结果Tab.5 Results of error analysis

相对误差及均方根误差常用以描述模型预测值与试验值之间的偏差，其数值越小，拟合偏差越小；RSquare 决定系数作为拟合优度的评价标准，表示了模型预测的数据变异性的比例，反映出模型对数据拟合的准确性，其数值越接近1，说明模型对数据的解释程度越高，即模型的拟合效果越好.结合图7、图8 与表5 可知，拟合的经验公式(10)与经验公式(11)的回归线与各试验及数值计算数据观测点接近，拟合效果较好、优度较高，保证了估算结果的可靠性与准确性.这说明所拟合的经验公式能满足两类传爆药的超压峰值预测以及威力评估要求.

4 结 论

本文通过对不同形状及密度的两类传爆药起爆后产生的冲击波超压峰值进行了试验研究、数值模拟以及经验公式优化，得到了如下成果：

(1) 在装药形状及爆距一定的情况下，随装药密度的增大，TATB 传爆药的超压峰值出现了先增大后减小的现象.分析认为TATB 传爆药密度增加，降低了炸药的冲击感度，药量的增加不足以抵消炸药未完全反应所带来的能量释放损失，使得其在高密度条件下超压峰值不增反减.

(2) 通过研究发现已有经验公式无法全面描述两类传爆药的超压峰值：在评估钝化RDX 传爆药时，理论计算结果整体偏高；对于TATB 传爆药的估算结果则误差较大.尤其是不同装药形状的传爆药，如能相对准确评估半球型RDX 传爆药超压峰值的Henrych 公式，在评估圆柱型RDX 传爆药超压峰值时不够准确.

(3) 拟合出了估算两类传爆药爆炸超压峰值的改进经验公式，将经验公式计算结果与试验仿真结果进行了对比分析，结果表明，改进经验公式适用于相应传爆药的超压峰值预测以及威力评估.