Al-PTFE 活性材料冲击释能行为及数值计算方法研究

卢冠成，刘振扬，袁盈，葛超，刘睿，陈鹏万，王海福

（北京理工大学 爆炸科学与技术国家重点实验室，北京 100081）

氟聚物基活性材料是一种具有类金属强度与类炸药能量的新型含能复合材料，在强冲击载荷下能够激活化学反应并释放化学能[1-2].凭借其动能侵彻与化学能释放的侵爆联合作用，活性材料毁伤元可有效提高各类战斗部的毁伤能力，已成为当前国内外高效毁伤研究领域的前沿热点方向[3].

与传统的含能材料如炸药、火药一经激活就会发生自持的化学反应不同，密实的活性材料内部无法持续传播稳定的化学反应[4]，其能量释放行为与材料的冲击加载条件密切相关.为了研究活性材料独特的能量释放特性，AMES[5]使用一种内部带有钢砧的密闭容器测量活性材料高速碰撞钢砧后的压力特性，从而分析材料的激活程度和释能特征.陈进等[6]改进了测试装置并通过火光与压力综合评估了活性破片能量释放特性.徐峰悦等[7]基于密闭容器测压方法进一步研究了容器前靶厚度对活性材料能量释放行为的影响.这些研究推进密闭容器超压测试成为活性材料能量释放特性研究的可靠方法.

在活性材料能量释放特性的数值模拟研究中，目前通常采用传统炸药或火药的状态方程来描述冲击激活与反应释能行为，如ROSENCRANTZ[8]、武强等[9]使用点火与增长模型，蒋建伟等[10]、王钊[11]使用混合JWL 模型，张雪朋等[12]使用Powder Burn 模型.为进一步提升这些模型对于材料冲击激活机理的描述，肖建光等[13]在点火与增长模型中引入了MOCK等[14]提出的应力-弛豫时间判据，从而唯象地模拟活性材料的冲击激活行为.但上述方法对于材料的冲击激活机理仍缺乏讨论，且材料单元的化学反应进程一经激活就将持续到反应完全，不能很好地表征活性材料的释能特性.

本文基于一种活性材料冲击引发化学反应理论模型，通过二次开发将其编译成力-热-化耦合的状态方程嵌入Autodyn 软件中，开展了活性材料密闭容器内爆能量释放实验，并验证了数值模拟方法的有效性.基于实验与仿真结果分析了不同撞击速度下活性材料冲击激活与能量释放特性，研究成果对活性材料冲击引发化学反应的数值计算方法发展具有重要意义.

1 活性材料冲击引发化学反应模型

1.1 模型简介

Al-PTFE 活性材料的能量释放行为是一种复杂的力热化耦合过程，在之前的研究中[15]一种描述该冲击引发化学反应行为的理论模型被提出，其中将Al-PTFE 活性材料在强动载下的能量释放行为分为冲击激活与化学反应两个阶段.

基于材料微观结构与细观动态力学数值模拟结果，引入热点理论描述活性材料冲击激活过程：在冲击载荷下，PTFE 基体内部孔隙部分快速变形、温度升高至PTFE 分解温度生成CF2气体，同时PTFE 基体局部发生破碎，使得Al 颗粒与CF2气体接触，引发后续化学反应.在此基础上提出了Al-PTFE 活性材料冲击激活判据，共两点：

① PTFE 基体中热点温度大于其分解温度，即

热点温度由下式计算：

式中：T*为热点温度；ρPTFE、cp与τ分别为PTFE 的密度、比热容与剪切强度；pg为初始孔隙内的气体压力，可认为等于大气压；r0和ri分别为初始孔隙半径和压缩后的孔隙半径.

② Al-PTFE 材料已经破碎失效，即

式中D为材料损伤度，可由强度与失效模型计算获得.

同时达到以上两点冲击激活判据后，材料进入化学反应阶段.该模型采用气固两相反应中的球核模型描述化学反应过程：PTFE 基体分解产生的CF2气体通过反应边界层向Al 颗粒扩散并发生反应，生成的AlF3气体同时通过边界层流出.化学反应速率由下式计算：

式中：CCF2为CF2的浓度[15]；rAl和ρAl分别为当前铝颗粒的半径和密度；F、T和p分别为当前材料的反应度、温度和压力；k为反应速率系数（由阿伦尼乌斯公式计算获得）；σAB和ΩAB分别为平均碰撞半径（0.435 nm）和碰撞积分（0.417）；MCF2和MAlF3分别为CF2和气态AlF3的相对摩尔质量；α为初始活性材料中的孔隙度.

1.2 模型嵌入开发

基于上节中的活性材料冲击引发化学反应理论模型，本文在Visual Studio 软件内编写Autodyn 软件提供的二次开发文件包内的mdeos_user_1.f90 子程序，以化学反应速率方程为控制项，定义并计算活性材料在未反应材料-混合材料-反应产物等阶段的p-V-T参数，即可在编译获得的Autodyn 用户自定义程序内使用本文开发的活性材料状态方程.

对于未发生反应的Al-PTFE 活性材料，使用Shock状态方程描述其状态.基于冲击Hugoniot 关系的Mie-Gruneisen 形式建立的Shock 状态方程形式如下，

假定Γρ= Γ0ρ0=常数，则有

式中：Γ 为材料的Gruneisen 常数，u= (ρ/ρ0)-1；ρ为材料实时密度；ρ0为材料初始密度；s为线性Hugoniot斜率系数；c0为体积声速.

对于反应产物，采用JWL 状态方程描述活性材料爆燃产物的扩散状态，其形式如下：

式中：A、B、R1、R2和ω为材料常数；E0为单位质量活性材料在空气环境中完全反应所释放的反应热，约为14.15 kJ/g；V为比容.

对于满足激活判据、已经激活化学反应的活性材料，引入化学反应度F来联系未反应材料和反应产物的状态方程.其中，F表示单元中已经反应结束转化成产物的材料的质量比例，F= 0 对应单元中全为未反应材料，F= 1 对应单元中全为反应产物，0 ＜F＜ 1 对应单元物质为包含未反应材料和反应产物的混合物.

当材料处于部分激活化学反应的混合状态时，假定未反应材料和反应产物这两种组分处于压力平衡状态，则有：

式中下标u 和p 分别代表未反应材料和反应产物.

混合状态材料的比内能E与比容V根据满足加和率：

式中：Eu和Ep分别为未反应材料和反应产物的比内能；Vu和Vp分别为未反应材料和反应产物的比容.

完成对上述物理量的定义后，就可以循环迭代计算温度、压力和反应度等物理量，计算流程如图1所示.物理量的具体计算方法与例程中点火与增长模型的二次开发方法[16]相同，只是将激活判据和反应速率方程替换成本文中的模型，本文不再赘述.

图1 循环内各物理量计算流程图Fig.1 Flow chart of calculating variables in single cycle

如图所示，计算循环开始时首先初始化变量，而后通过反应度F判断材料是否发生激活，未激活材料使用未反应材料状态方程进行计算，已激活材料则继续判断是否处于混合物状态，如材料反应完全，则使用JWL 状态方程进行计算，否则使用混合材料状态方程计算.计算混合材料状态方程时，首先预估温度，而后根据压力平衡假设，使用比容和反应度迭代计算，直至配平本循环中的两种组分的压力；再使用本循环得到的新压力校准预估温度.最后根据反应速率方程计算当前步长的反应度增量和材料体积声速，完成一个循环中所有物理量的计算工作.

2 冲击释能行为测试方法

2.1 数值模拟计算模型与材料参数

在Autodyn 用户自定义程序内，建立活性材料破片密闭容器内能量释放典型计算模型，模型由活性材料破片（以下称活性破片）、容器（以下称测压罐，简化为圆柱罐体与砧板）与前置铝板组成，为提高计算效率采用1/4 对称模型，如图2 所示.由于Lagrange 算法运用于大变形问题时，需配合侵蚀算法以保证计算稳定性，而侵蚀算法会造成材料质量与能量损失，因此采用SPH 算法描述活性破片与前置铝板.活性破片材料尺寸为Φ10 mm × 10 mm，SPH 粒子间距为0.5 mm；前置铝板长×宽×高尺寸为200 mm ×200 mm × 3 mm，SPH 粒子间距为1.0 mm.测压罐几乎不发生变形，可采用Lagrange 算法描述.测压罐体内部尺寸为Φ300 mm × 378 mm，前后壁厚10 mm，前壁开孔Φ100 mm，侧壁厚5 mm；砧板尺寸为Φ200 mm ×20 mm，砧板后壁与罐体后壁内侧距离90 mm.表1为活性材料状态方程主要参数[17]；表2 为活性材料Johnson-Cook 强度模型和失效模型参数[18].

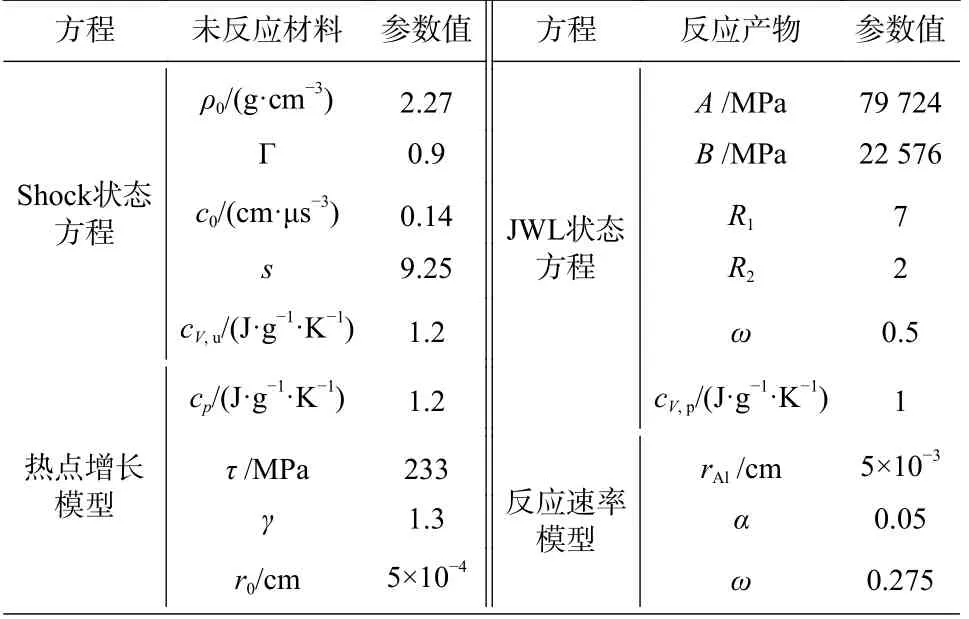
表1 活性材料状态方程主要参数Tab.1 Main parameters of EOS of reactive materials

图2 典型计算模型Fig.2 Typical simulation model

2.2 实验方法与布置

为验证活性材料自定义状态方程与数值计算方法有效性，开展了活性材料密闭容器内爆能量释放实验.实验原理如图3 所示，主要由弹道枪、测速靶、测压罐与超压测试系统等组成.由弹道枪发射嵌入弹托内的活性破片，由测速仪测量破片速度，由超压测试系统测量反应压力数据，并由高速摄影观测反应过程.

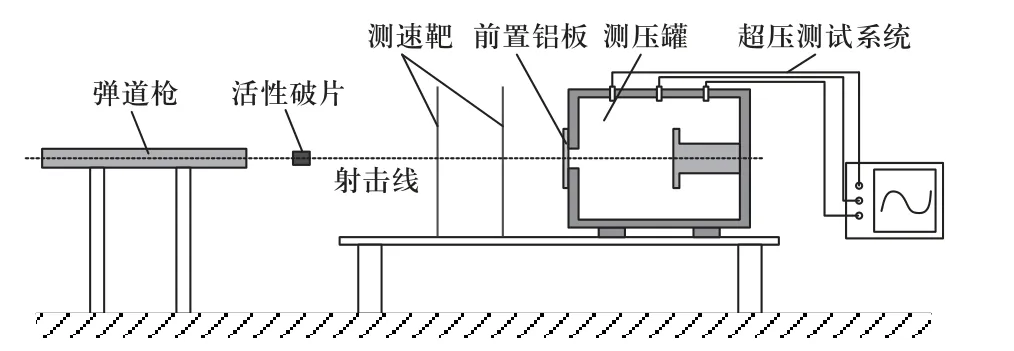
图3 实验原理示意图Fig.3 Schematic diagram of experiment

在700～1 300 m/s 速度范围内共进行5 发不同冲击速度下的超压测试实验，活性破片采用零氧平衡配比的Al-PTFE 粉末（组分质量比为73.5/26.5）经过混合模压烧结制备而成，理论密度为2.39 g/cm3，实测密度为2.27 g/cm3，孔隙率约为5%，破片尺寸为Φ10 mm × 10 mm，质量约为1.78 g.测压罐容积为27 L，顶部安装3 枚压力传感器，前壁开口处使用厚度为3 mm 的铝板压紧密闭，侧壁设置观察窗以便通过高速摄影观察内部反应现象，如图4 所示.

图4 实验用测压罐Fig.4 Test chamber used in experiment

3 结果与分析

3.1 实验结果与对比分析

在1 019 m/s 速度下，活性破片在测压罐内冲击释能行为典型高速摄影照片（帧率10 000 fps）如图5所示.以活性破片撞击前置铝板为计时原点，在200 μs时刻罐内前部观察到火光，破片从火光中飞出，表明部分破片在碰撞前置铝板已经激活并发生反应.在500 μs 时刻，罐内观测到明亮火光，表明剩余活性破片碰撞砧板后大量激活并发生剧烈反应，大量释放能量.在1 600 μs 时刻，罐前火光基本消失，表明碰撞前置铝板激活的活性破片反应基本结束，直到4 800 μs 时刻罐内火光基本消失.

图5 实验过程典型高速摄影（速度v =1 019 m/s）Fig.5 Typical high-speed photography of experiment process (impact velocity v=1 019 m/s)

对应速度下数值模拟中各时刻反应度云图如图6 所示，图中隐藏了前置铝板以清晰显示侵孔内活性破片的反应情况.在200 μs 时刻，活性破片穿透铝板后部分碎裂，少量已激活化学反应的飞散碎片残留在铝板前后和侵孔中，剩余主侵彻体向罐内飞入且并未激发大范围反应；剩余碎片主体于525 μs时刻碰撞砧板并于600 μs 时刻显著破碎变形，引发前部径向外侧的材料激活并发生化学反应.在950 μs 时刻，碎片内部被激活的材料进一步发生反应，释放反应产物推动解体后的剩余碎片向外运动.在1 600 μs 时刻，断裂的小部分碎片碰撞砧板，但由于剩余速度太低基本无法激活，反应产物进一步飞散，直至3 000 μs 时刻分布较为均匀.

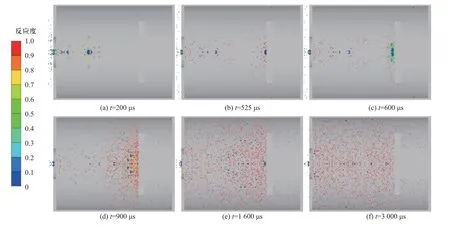
图6 数值模拟典型反应度云图（v =1 000 m/s）Fig.6 Typical reaction content cloud map of simulation result (impact velocity v=1 000 m/s)

压力传感器采集到的信号经过放大和数据处理后获得的超压时程曲线如图7 所示，图中5 条曲线对应5 发不同速度工况下3 枚传感器测量结果的平均值，活性破片在测压罐内反应释能造成的超压随碰撞速度提高而增大.

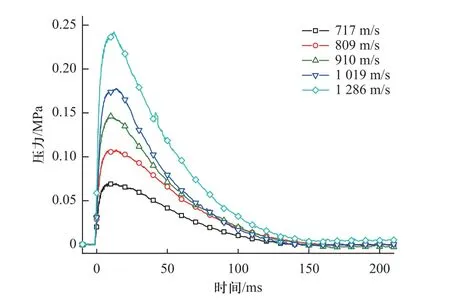
图7 压力时程曲线Fig.7 Pressure-time curves

受Autodyn 用户自定义子程序计算效率与SPH算法计算规模限制，数值模拟中并未建立罐内空气域模型，因而无法通过在对应位置设置观测点直接获得活性材料反应向空气传播的压力时程曲线，故本文采用活性破片在罐内的释能量这一特征量作为验证参量.AMES[19]将活性破片贯穿前置靶板并在测压罐内的能量释放过程简化为绝热等容过程，基于理想气体状态方程与能量守恒关系获得了超压与测压罐系统内能变化关系：

式中：Δp为峰值超压；V为测压罐容积；ΔU为测压罐系统内能变化量；γ为罐内空气的绝热指数，通常取γ= 1.4.

则活性破片在测压罐内的释能量ΔE等于测压罐系统内能变化量ΔU：

根据该式可计算出实验中不同速度下活性破片的释能量，结果列于表3.

表3 实验结果Tab.3 Experiment results

数值模拟中活性破片在测压罐内反应释能量ΔEt按以下方法计算获得，其中各广度量如质量与能量为全模型下数据：

式中：Emax为活性破片的理论最大释能量；E0为单位质量活性材料的反应热；m为活性破片质量；mi与Fi分别为活性破片单个SPH 粒子的质量与反应度；Ft为活性破片总反应度.

通过计算获得数值模拟中不同速度下活性破片的释能量，结果列于表4.

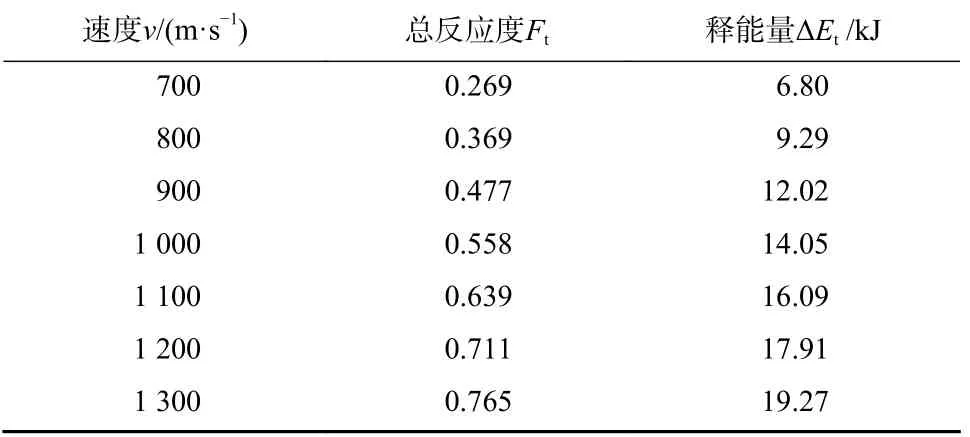
表4 数值模拟结果Tab.4 Simulation results

将数值模拟获得的不同速度下活性破片反应释能量ΔEt与根据实验数据计算获得的活性破片释能量ΔE进行对比，结果如图8 所示.各速度下数值模拟结果均大于实验计算结果，偏差分别为45.4%、27.8%、21.7%、18.6%与18.0%，平均偏差为26.3%.一方面，数值模拟结果统计的是活性破片整体，实验中观测到的罐前明亮火光表明部分破片在罐体外部发生反应，如图5 所示；另一方面，实验所用活性破片质量较小释能较少，罐内气体压力在达到峰值时不足以维持高于196 kPa 密闭压力条件[20]，发生泄压导致能量有一定损失.

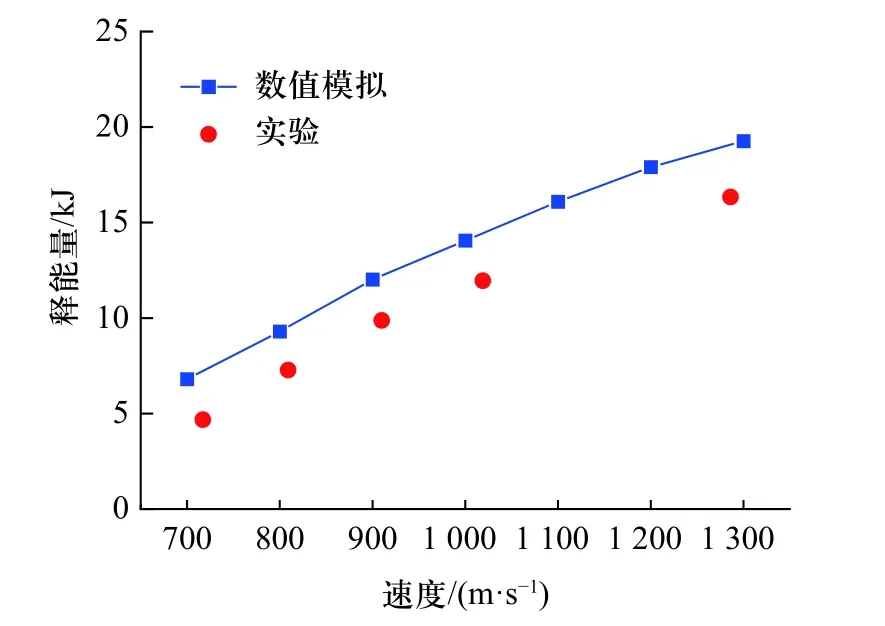
图8 数值模拟与实验结果对比Fig.8 Comparison of energy in simulation and experiment

3.2 能量释放行为过程分析

不同速度下对应典型时刻的数值模拟反应度云图如图9 和图10 所示，图中同样隐藏了前置铝板.为与图6 中1 000 m/s 速度下数值模拟结果对比，各时刻选择依据与前文相同，分别为破片初始碰撞铝板后200 μs 时刻，碎片主体二次碰撞砧板时刻，碰撞砧板后75 、375 、1 075 μs 时刻与计算停止时刻.

图9 数值模拟典型反应度云图（v =700 m/s）Fig.9 Typical reaction content cloud map of simulation result (impact velocity v=700 m/s)

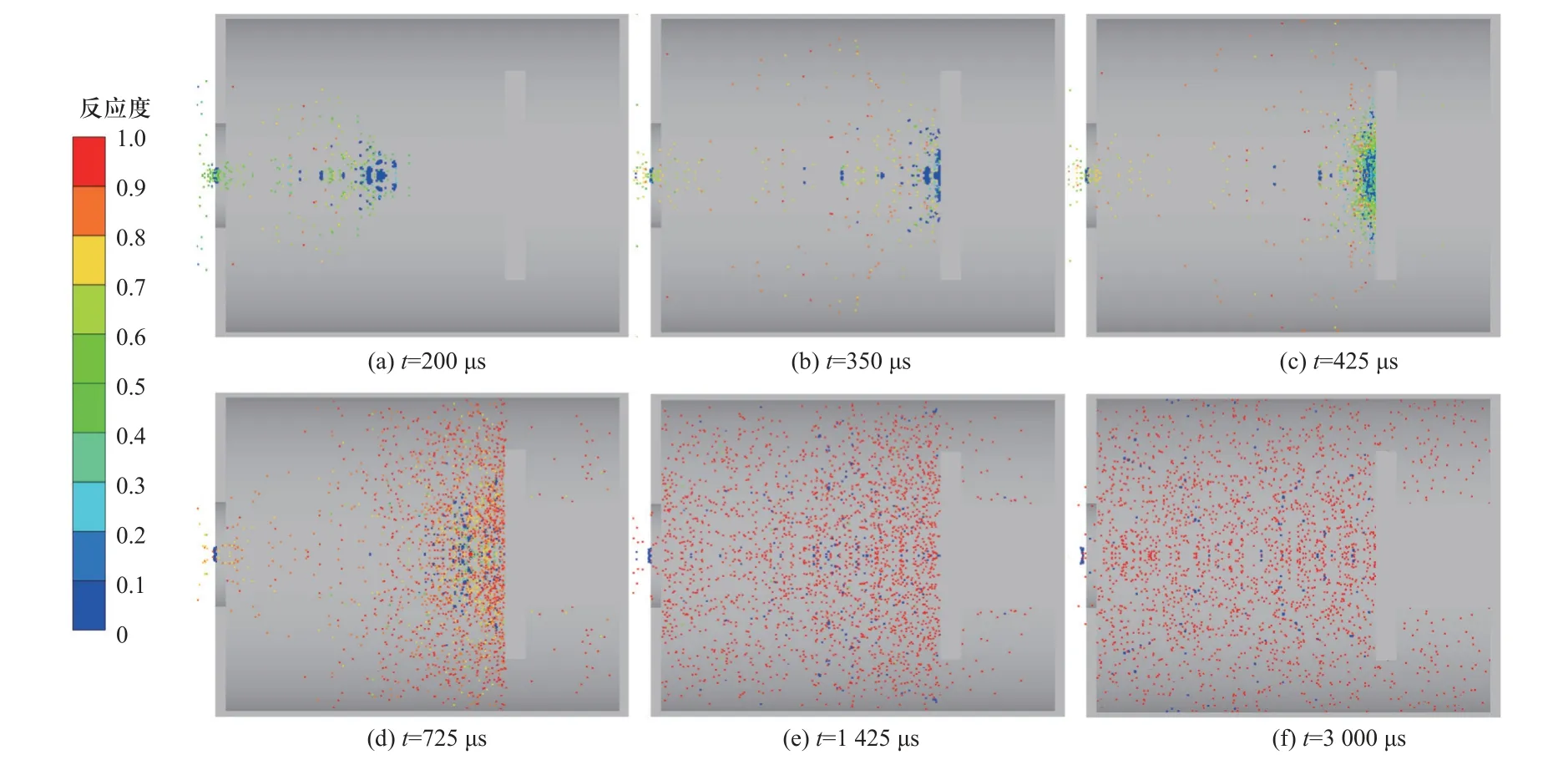
图10 数值模拟典型反应度云图（v =1 300 m/s）Fig.10 Typical reaction content cloud map of simulation result (impact velocity v=1 300 m/s)

活性破片碰撞并穿透铝板后，破片外表层材料因抗拉强度较低首先破碎飞散，同时由于初始撞击加载被激活，残留在铝板穿孔附近发生反应.活性破片径向内部的材料发生不规则破碎，形成数量不等的碎片，速度越高，形成的碎片质量越小、速度差越低.碎片断裂面处的活性材料完全破碎失效，被激活并发生化学反应，且速度越大，被激活的材料质量越大，材料化学反应速率越高.而碎片内部材料累积了一定损伤度但并未失效，因此并未被激活.

对于向罐体内部飞散的速度较高的活性材料碎片，二次碰撞作用使其内部材料完全失效、温度快速上升并充分激活，进入快速化学反应阶段，如图11所示.同时，观察到前部碎片反应产生的高压气体产物体积膨胀并反推后部速度较低的碎片，阻碍其二次碰撞激活，且碎片剩余速度越低该现象越明显.这是由于二次碰撞的冲击强度与活性材料碎片质量与碰撞速度正相关，碰撞速度较高时，二次碰撞激活的活性材料明显更多，反应也更加剧烈.不同速度下活性破片总反应度随时间变化关系如图12 所示，曲线拐点对应活性破片二次碰撞激活引起的反应.随着碰撞速度增大，活性破片总反应度与反应速率明显提升，且活性破片的最终总反应度远高于发生二次碰撞前累积的总反应度，表明活性破片反应释能量主要由高速碎片二次碰撞提供，与前文定性分析一致.

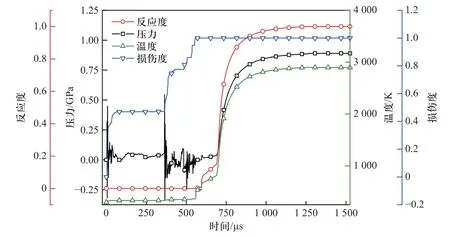
图11 活性材料碎片内部典型观测点数据（v =1 300 m/s）Fig.11 Typical gauge data in reactive material fragment (impact velocity v=1 300 m/s)

图12 不同速度下总反应度时程曲线Fig.12 Total reaction content-time curves at different velocities

为分析活性破片能量释放过程各阶段反应强度，统计了各工况中正在进行化学反应的活性材料粒子数占总粒子数之比，结果如图13 所示.总体而言，按反应粒子数占比可将活性破片的整体反应过程分为3 个阶段：平台段、上升段与下降段.

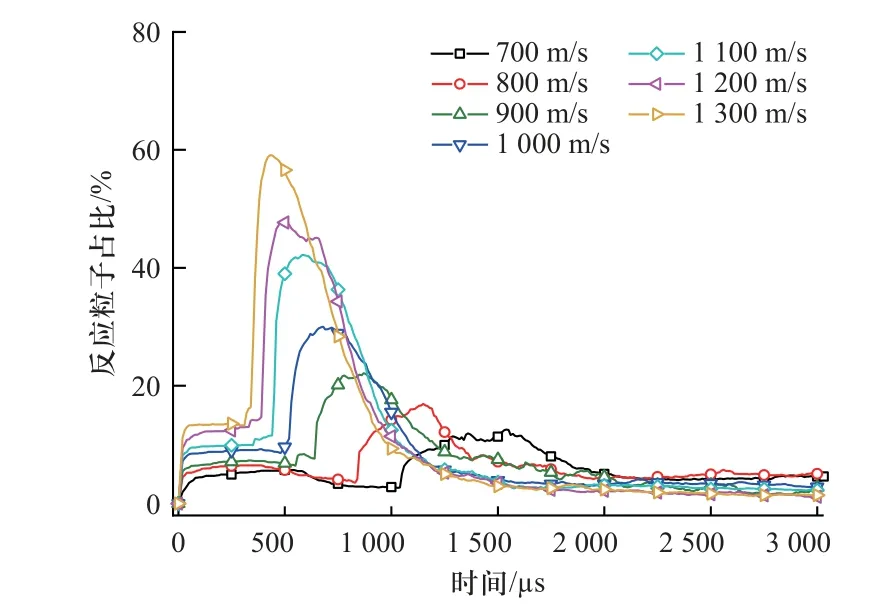
图13 不同速度下反应粒子占比Fig.13 Proportion of reacting particles at different velocities

平台段为活性破片初始碰撞铝板到二次碰撞砧板之前，此阶段发生反应的活性材料完全由初始碰撞激活.由于化学反应时间（数百μs 至ms 量级）与破片两次碰撞间隔时间基本相当，反应粒子占比较为稳定，总反应度开始累积，对应图12 中总反应度的第一次上升的过程.此外，当碰撞速度较低时，部分粒子在破片二次碰撞前就已反应完全，导致反应粒子占比有所下降.

上升段为活性破片二次碰撞砧板快速激活阶段，此阶段发生反应的活性材料主要由二次碰撞激活，上升段峰值与平台段之差反映二次碰撞激活粒子数.随着碰撞速度提升，二次碰撞激活的材料快速增加，且在总体激活材料中的占比显著上升.该阶段，激活反应的材料粒子占比快速增加，同时该部分材料反应快速进行，对应图12 中总反应度第二次上升的过程.

下降段为活性破片反应衰减阶段，此阶段碎片主体二次碰撞激活过程已经结束，且后续低速碎片基本无法激活.同时，已激活粒子的反应随着时间推移逐渐结束，使得反应粒子占比不断下降并最终接近零点，活性破片能量释放过程基本结束，对应图12 中总反应度逐渐累积至最终值的过程.

4 结 论

本文基于本文活性材料冲击引发化学反应理论模型开发了冲击释能行为数值计算方法，对活性破片在密闭容器内反应释能过程进行了数值模拟并与实验结果进行了对比.得到的主要结论如下：

① 数值模拟中材料反应度与实验中火光变化趋势一致，获得的材料释能量与实验结果平均相差26.3%，表明基于理论模型的状态方程可以较好地反映活性破片能量释放行为，改进后可用于精确描述活性材料的释能特性.

② 活性破片穿透前置铝板后，破片外表层材料在铝板穿孔附近率先碎裂并发生反应，径向内部材料断裂破碎，碎片断裂面处的材料被激活，预先积累了一定损伤度的碎片内部材料于二次碰撞砧板过程中大量激活并发生快速化学反应.

③ 活性破片碰撞密闭容器能量释放过程可分为初始碰撞少量激活的平台段、二次碰撞激活的快速上升段与整体反应衰减的下降段三个阶段，且释能量与化学反应速率随碰撞速度增加而快速提升.