爆轰驱动下轴向预制破片飞散特性研究

李正川,何 源,郭 磊,王传婷,何 勇,马 跃

(南京理工大学 机械工程学院,江苏 南京 210094)

传统预制破片战斗部是将破片布置在装药周围,炸药爆炸后驱动周向破片高速飞出,利用破片的高速动能实现对目标结构的毁伤,然而破片周向排列方式将导致战斗部在单一方向上有效破片数量少,打击效率降低。为更大效率地发挥战斗部对固定方向上的毁伤威力,有学者提出了定向战斗部[1]的概念,轴向预制破片战斗部是其中的一种,它将预制破片排列于装药端面,引爆装药后,预制破片会沿装药轴线方向向前运动,具有定向毁伤拦截的特点,并且可以改变炸药端面的曲率以控制破片场的有效毁伤范围。目前,以轴向预制破片形式设计的拦截弹已应用于武装直升机等机载主动防御系统中,如美国“直升机主动RPG防护”系统[2]。

为了研究轴向战斗部多层预制破片层间速度大小、飞散角分布的影响因素,国内外学者针对轴向预制破片战斗部破片飞散情况展开了系统的研究。JONES[3]基于能量守恒定律和Gurney假设推导了多层破片速度的理论计算方法,为爆轰驱动多层预制破片的相关研究提供了理论支撑。文献[4-5]针对单层轴向预制破片战斗部进行了研究,基于Gurney公式,得到了轴向单层预制破片速度和飞散角的计算公式。李明星[6]利用理论和数值方法对单层球形、方形和圆柱形轴向预制破片的飞散特性进行研究,结果表明球形破片速度和飞散角均大于其他形状破片。MA等[7]针对轴向单层预制破片在不同衬层下的爆轰驱动过程进行了试验和数值研究,并与无衬层形式进行对比,结果表明,凯夫拉/环氧树脂衬层使得破片的初速度低于无衬层形式下的破片速度,并且球形破片在爆轰驱动方面优于圆柱形破片。文献[8-9]基于改进后的Gurney公式得到了多层球形破片在爆轰驱动后的破片平均速度,结合Taylor公式得到了破片的飞散范围角,并通过实验验证了理论结果的合理性。文献[10-11]研究了弧形装药结构下多层球形破片的飞散情况,得到了带弧形圆柱装药下,从内往外球形破片的平均初速逐层增加,以及随着球形破片直径减小最内层破片初速增大的规律。

目前,有关多层轴向预制破片的研究通常将金属破片层看作一个金属板[12-14],分析金属板的初速得到破片的近似速度,并未涉及到破片层间的相互作用关系。本文针对多层预制破片在炸药爆轰驱动后的层间速度关系问题,基于Gurney假设和动量守恒定律得到了轴向预制破片战斗部多层破片初速的近似计算模型,并进行了破片爆轰驱动过程动力学仿真,分析了不同破片形状对于多层破片初速的影响,以及破片层数对于破片初速的影响,为提高战斗部的毁伤威力设计提供一定的参考作用。

1 破片层初速理论计算模型

1.1 速度计算模型

本文采用圆柱形装药结构,不同形状的预制破片排布在炸药端部的隔板上,并用树脂黏结剂固化黏结在一起。为建立不同形状的多层破片初速理论计算公式,作如下假设:

①破片前置且按轴向分层排列,球形破片和圆柱形破片均采用密排方式,破片间隙采用树脂黏结剂填充,忽略其对破片飞散特性的影响,只考虑质量。炸药采用中心点起爆方式。

②炸药瞬时爆炸,释放的能量全部用于破片和爆轰产物的飞散,爆轰产物不通过预制破片的间隙向外溢出。

③爆轰产物从起爆端面到球形破片内切面、圆柱破片底面、方形破片底面之间的速度呈线性分布,并且与第一层破片接触的爆轰产物的速度与该层破片速度相同。

在炸药爆炸驱动多层破片飞散过程中,分别用mi,vi(i=1,2,…,n)表示从靠近炸药到远离炸药的第i层破片的质量和速度,由于相邻破片层之间的排列方式相同,假设相邻破片层之间的速度比值相同,即vi+1/vi=k。

图1 理论模型示意图Fig.1 Schematic diagram of the theoretical model

由动量守恒得到预制破片与爆轰产物的运动方程:

(1)

式中:mc为炸药爆炸前的质量,mc/2为炸药爆炸后爆轰产物的虚拟质量,m为破片层中树脂黏结剂、隔板和壳体的总质量,S为爆轰产物作用于端面第一层预制破片的有效面积,p为某瞬间爆轰产物作用于预制破片层的压强。同时,假设炸药半径为r0,炸药密度为ρ0,r为爆轰产物的膨胀后与装药轴线的距离。

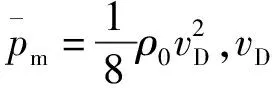
(2)

设S=λS0,λ为轴向预制破片数量和r的因变量。当预制破片结构尺寸和多层破片排布方式确定后,定有常数0<ε≤1,使得:

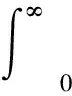
(3)

将式(2)、式(3)代入式(1),并整理可得到:

(4)

式中:r≥r0。所以最内层破片初速为

(5)

对于球形破片,有:

(6)

对于方形破片,有:

(7)

对于圆柱破片,有:

(8)

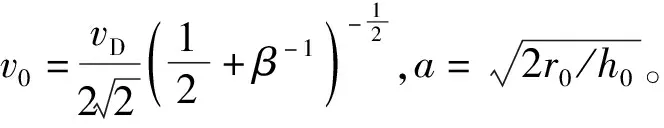
vi=k(i-1)v1=k(i-1)aψ(n1)v0

式中:k与破片层数i、最内层破片数n1有关。针对于不同形状多层破片的k值,可通过数值仿真的结果来确定。

1.2 破片飞散角计算模型

图2 飞散角计算示意图Fig.2 Schematic diagram of dispersion angle calculation

2 仿真分析

2.1 战斗部有限元模型

本文使用非线性有限元计算程序LS-DYNA和网格划分软件True-Grid分别对球形、方形、圆柱形3种破片进行爆轰驱动数值模拟分析,战斗部结构包括炸药、空气、隔板、壳和预制破片。战斗部数据如表1所示。战斗部壳体厚度为1 mm,各工况下壳体质量如表2所示。

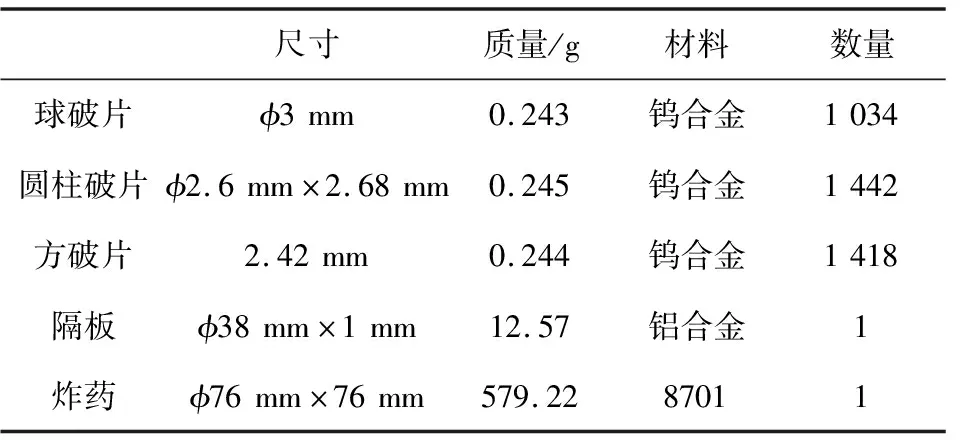
表1 战斗部数据Table 1 Warhead data

表2 各工况壳体质量Table 2 Shell quality under different conditions

其中,每层球形破片和圆柱破片均为密排方式,树脂黏结剂采用环氧树脂。以球形破片为例,战斗部模型如图3所示,在各工况下,将球形、方形和圆柱形多层破片的每层破片按图4的方式分为不同列,并记为第1,2,…,i列。

图3 两层球破片战斗部示意图Fig.3 Schematic diagram of two-layer ball-fragment warhead

图4 破片分列示意图Fig.4 Schematic diagram of fragmentary distribution

为节约仿真计算时间,提高计算效率,考虑到战斗部的对称关系,采用1/4战斗部模型进行仿真分析。破片、壳体和隔板采用Lagrange网格,炸药、空气和树脂黏结剂采用Euler网格。针对流体网格和固体网格在数值计算中的优缺点,本文采用ALE多材料、流体/结构耦合算法进行计算。对于Lagrange区域重叠欧拉网格区域的问题,本文仿真中采用*CONSTRAINED_LAGRANGE_IN_SOLID关键字来实现流体-结构间的相互作用,拉格朗日网格与ALE(流体)网格在空间上重叠,每个网格都用独立的节点id来定义,LS-DYNA搜索拉格朗日网格和ALE网格之间的空间交点,当网格重叠时,发生相互作用。破片与破片、隔板与破片以及破片和壳体间设置为自动单面接触,炸药采用单点起爆方式,起爆点设置在炸药底面圆心处。

2.2 材料模型和参数

空气材料采用MAT_NULL模型和线性多项式状态方程(EOS_LINEAR_POLYNOMIAL)。炸药采用高能炸药燃烧材料模型(HIGH_EXPLOSIVE_BURN)和JWL状态方程,材料参数如表3所示。表中,pCJ为爆轰压力;A,B,R1,R2,ω为炸药材料参数。

表3 炸药材料参数Table 3 Material parameters of explosive

壳体和隔板材料模型均采用Johnson-Cook模型和Gruneisen状态方程,材料参数如表4所示。表中,A为材料初始屈服应力,B为应变硬化系数,n为应变硬化指数,C为应变率系数,m为热软化指数。

表4 壳体和隔板材料参数Table 4 Material parameters of shell and baffle

破片材料采用MAT_PLASTIC_KINEMATIC模型,并添加沙漏(HOURGLASS)控制,材料参数如表5所示。表中,E为杨氏模量,ν为泊松比,σ0为屈服应力。

表5 破片材料参数Table 5 Material parameters of explosive

树脂材料采用MAT_ELASTIC_PLASTIC_HYDRO模型和GRUNEISEN状态方程,材料参数如表6所示。表中,G为剪切模量,σ为屈服应力。

表6 环氧树脂材料参数Table 6 Material parameters of epoxy resin

3 分析与讨论

3.1 破片飞散仿真分析

本文针对球形、方形和圆柱形破片的爆轰驱动数值仿真分别设置了两层和三层破片的工况,共6种工况。由于各工况下爆轰产物与破片间的作用效果相似,故本文以球形破片战斗部为例,爆轰产物与破片间的作用示意图如图5所示。可以看出破片与爆轰产物之间存在相互作用关系,破片在爆轰产物的作用下向前运动。

图5 爆轰产物与破片相互作用示意图Fig.5 Schematic diagram of interaction between detonation product and fragment

不同形状破片情况下爆轰波的传播情况相似,各工况下多层破片爆轰驱动飞散过程如图6所示。从图6可以看出爆轰波在t=90 μs左右时到达最内层破片的下表面,战斗部轴线周围破片首先受到爆轰波的推动作用开始向前运动,t=180 μs时,破片已在空气中运动。炸药爆炸后产生的爆轰波以及爆轰产物首先作用到隔板上,由于在极短的时间内隔板处爆轰产物压力急剧增大,最高可达61.39 GPa,且由于隔板薄以及隔板本身材料的原因,隔板迅速变形以致破坏失效,然后爆轰产物再作用到第一层破片下表面,破片开始向前飞散并与第二层破片发生碰撞,相同时刻下,外层破片飞行距离较远。

图6 各工况下多层破片飞散示意图(单位:GPa)Fig.6 Schematic diagram of multi-layer fragmentation dispersion under various working conditions(unit:GPa)

图7为破片碰撞速度变化示意图。可以看出,第一层破片在与第二层破片发生碰撞后,第一层破片速度会发生衰减,同样第二层破片在和第三层破片发生碰撞后也会发生衰减,然后在爆轰产物的作用下继续加速,最后各层破片速度达到稳定的状态。同时,第一层破片在与第二层破片、第二层破片与第三层破片发生碰撞前,第二层破片和第三层破片已经受到爆轰波的加速作用。

图7 破片碰撞速度变化示意图Fig.7 Variation of fragments collision velocity

图8为不同工况同一时刻下,多层破片飞散速度云图。可以看出,炸药爆炸后,破片会沿着战斗部轴向和径向飞散,由于爆轰波先到达战斗部轴线附近的破片,故相同时刻下破片的最大速度出现在破片层中心位置。从各工况的速度云图可以看出,最大动能均出现在破片层的中心位置,也即红色区域,从内往外破片动能减少,两层球破片和三层球破片的第一层边缘破片最大平均速度分别为977.6 m/s和749.3 m/s,超过了蓝色区域破片的速度,并且从图7(a)中可以明显看到,第一层边缘破片已超过第二层蓝色区域破片,其余图中也可看出边缘破片超过非边缘破片的趋势,这是由于爆轰产物在破片层边缘位置发生绕流,并且边缘位置破片约束较少,进一步加速了边缘位置的破片,其中球形破片受到绕流加速作用的效果最为明显。

图8 多层破片飞散示意图(单位:m/s)Fig.8 Schematic diagram of multi-layer fragment dispersion(unit:m/s)

3.2 数值仿真与理论计算结果分析

图9为破片速度稳定后,各层各列破片速度平均值以及每层破片速度平均值。可以看出各工况下的数值仿真结果中,各层破片速度分布合理,沿半径方向同列破片速度梯度越来越大,两层破片情况下,各列破片最大速度差值:球破片为42.9 m/s,方破片为30.78 m/s,圆柱破片为12 m/s;三层破片情况下,第一层和第二层破片间,各列破片最大速度差值:球破片为48.2 m/s,方破片为19.2 m/s,圆柱破片为8.3 m/s,;第二层和第三层破片间,各列破片最大速度差值:球破片为57.2 m/s,方破片为28.2 m/s,圆柱破片为10.1 m/s,显然球破片的速度梯度相对方形和圆柱形破片更大,同时,对于不同类型破片,以上差值分别取自不同的列位置,其中只有球形破片取自破片层边缘位置,说明在爆轰产物绕流作用、边缘位置破片束缚较少以及球形破片受到的阻力相对于方形和圆柱形较小的多方影响因素下,同列位置内层破片速度更高于外层破片。三层球形破片和方形破片的工况仿真结果中,存在明显的破片层边缘处破片受到绕流加速的作用后速度变大的情况,与前文分析一致。

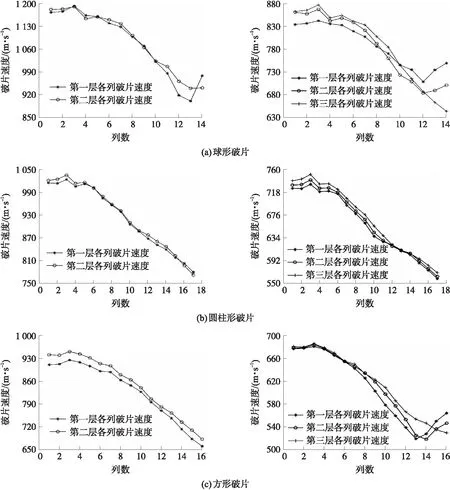
图9 各列破片速度Fig.9 Fragment velocity of each column

表7～表9为不同工况下破片速度计算值和仿真值。可以看出,对应层数破片工况下,球形破片初速平均值大于圆柱破片初速平均值,对应层数圆柱破片初速平均值大于方破片初速平均值,其原因为:①球形破片相对于其他两种类型破片的平均迎风面积小,受到的空气阻力小,导致在相同飞散距离内破片速度衰减较弱;②在相同破片材料情况下,单枚破片质量均相同,而不同形状破片的空间占有率不同,所以相同层数破片数目不同,最终战斗部装填比不同,导致球形破片一开始初速也会高于其他破片;③边缘位置破片在爆轰产物绕流加速后导致整体速度平均值上升。两层破片情况下,圆柱破片速度计算值与仿真值最为接近,误差为2.2%,三层破片情况下,球破片速度计算值与仿真值最为接近,误差为1.2%;随着破片层数以及破片数量的增加,最内层破片初速逐渐减小;相邻层之间破片平均初速的比值几乎相等。

表7 球破片初速理论计算值和仿真值Table 7 Theoretical calculation and simulation values of initial velocity of ball fragments

表8 圆柱破片初速理论计算值和仿真值Table 8 Theoretical calculation and simulation values of initial velocity of cylinder fragments

表9 方破片初速理论计算值和仿真值Table 9 Theoretical calculation and simulation values of initial velocity of square fragments

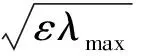
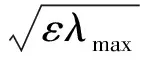
3.3 破片飞散角讨论

仿真结果结合简化平均飞散角计算模型得到的破片飞散角如图10和图11所示。

从图中可以看出,两层破片情况下,方破片内层破片飞散角度小于外层破片,同层破片从内往外破片飞散角度先增大后减小;对于球破片,整体上内层破片飞散角小于外层破片的规律,而在破片层边缘位置,则存在内层破片飞散角大于外层破片的情况,这也说明了内层边缘破片受到爆轰产物绕流加速作用后速度高于外层破片;圆柱破片内层和外层破片飞散角较为一致,均在17°～22°范围内,不同层破片间飞散角差值较小,同层破片的每列破片飞散角分布较为均匀。三层破片情况下,方破片飞散角度从内层破片到外层破片逐渐增大,对于同层破片,沿半径方向破片飞散角呈先增大后减小的趋势;对于球破片而言,最外层破片飞散角均小于同列内层破片,而沿半径方向破片飞散角逐渐增大;同列圆柱破片从最内层到最外层破片飞散角呈逐层增加的趋势,但整体上内层和外层破片角度分布在19°～24°范围内,同层每列破片的飞散角分布较为均匀。

整体而言,对于不同类型破片的飞散角存在一定的差异,圆柱破片飞散角较为均匀,球破片沿半径方向飞散角逐渐增大,而方破片的边缘位置破片飞散角为最小值,本文认为是边缘位置破片数量较少导致数据存在一定的偏差,再者考虑到破片形状的差异、迎风面积的影响导致各类型破片的飞散程度存在差异。

4 结束语

本文基于Gurney假设和动量守恒,建立了轴向预制破片不同层间的初速近似计算简化模型,首先通过理论计算,得到多层破片的第一层破片初速,然后利用LS-DYNA软件进行数值仿真,得到多层破片各层破片速度平均值和层间速度比值,最后结合层间速度比值得到各层破片的平均速度理论计算值。研究结果表明:

①沿半径方向破片速度梯度先减小后变大,相同层数时,球形破片速度梯度最大;随着破片层数增加,破片速度梯度增加;相同形状破片的平均速度从最内层到最外层逐渐增加。

②对于三种破片形状,球形破片的平均速度最大,并且层间速度差值最大,两层破片排布与三层破片排布时层间速度差值相接近;球破片、圆柱破片和方破片的理论模型计算值与仿真值间的误差最低分别为1.2%,2.2%,8.8%,再次说明速度计算模型可以较好反映出圆柱装药下不同形状轴向多层预制破片初速情况。

③各列圆柱破片飞散角分布在相同范围内,球破片沿半径方向飞散角有增大趋势;在相同层数情况下,方破片的飞散角度小于圆柱破片和球破片,破片飞散角的分布规律和破片形状密切相关。综合破片平均速度和飞散角可以认为球形破片飞散性能较好。