变压器绕组松动故障的混沌特征分析方法*

薛健侗, 马宏忠

(河海大学 能源与电气学院,江苏 南京 211100)

0 引 言

电力变压器作为变电站的核心设备,承担着电力转换、传输的关键枢纽作用[1-2]。因此,变压器的安全持续运行关乎电力系统的稳定运转。然而,相关资料显示,变压器绕组由于在运输安装过程中受到冲撞,加之长期承受不规律短路电流的冲击,使得变压器绕组松动故障成为变压器事故的首要原因[3]。目前,振动法被广泛应用于变压器等电力设备的运行状况检测[4-5],这是因为其在检测中无需与电力设备有电气联系,是一种无损测量方式。

对于变压器振动信号的处理方法通常为时频分析法。文献[6]提出了采用小波包变换对变压器振动信号进行分解并组成能量特征向量,输入到模糊自适应共振理论(Fuzzy-ART)神经网络实现故障准确分类。文献[7]基于快速傅里叶变换(FFT)频谱分析,确定振动信号中变压器绕组松动故障特征频率为100 Hz,提出了绕组松动诊断模型,实现了定量判断绕组松动状态。文献[8]采用变分模态分解方法处理变压器空载合闸振动信号,建立信息熵-峭度-相关系数综合评价模型并运用熵权-优劣解距离法(TOPSIS)法提取特征模态分量,实现变压器绕组松动有效识别。上述时频分析法在处理变压器振动信号时或多或少都会使得原始信号损失部分精度,可能会将故障特征误除。

相对于时频分析法,基于混沌理论的相空间重构技术能够将非线性动力系统的时间序列信号隐藏的信息充分地展示出来。文献[9]采用平均位移法确定延迟时间,重构出变压器振动信号的二维相空间轨迹,定性分析了绕组松动状态下的相空间轨线为空心畸变椭圆,而绕组压紧状态对应的轨线则并未沿主对角线打开,据此实现了变压器绕组松动故障识别。

基于此,本文提出了一种变压器绕组松动故障的混沌特征分析方法。首先验证了变压器振动信号的混沌特性,进而采用互信息量法[10]和G-P算法[11]求得对应的延迟时间τ和嵌入维数m,然后对绕组处于不同状态下的变压器振动信号进行相空间重构,分析了相空间轨迹随绕组松动故障程度加深的变化规律,并计算其关联维数、Kolmogorov熵和最大Lyapunov指数组成混沌特征用以定量识别绕组松动故障。

1 变压器振动信号的相空间重构

在解决实际问题时,为了恢复信号蕴含的混沌特性水平,将其可视化,一般需要对其进行相空间重构。通常的做法是将一维的时间序列扩展至更高维的空间,这样便可以从中提取和恢复系统原来的规律,而这种规律是高维空间下的一种轨迹[12-13],信号隐藏的信息就能够被充分地挖掘出来。具体过程如下:

对于变压器振动信号时间序列xi=[x1,x2,…,xN],其中N为序列长度。采用坐标延迟法[14-15]重构相空间后为

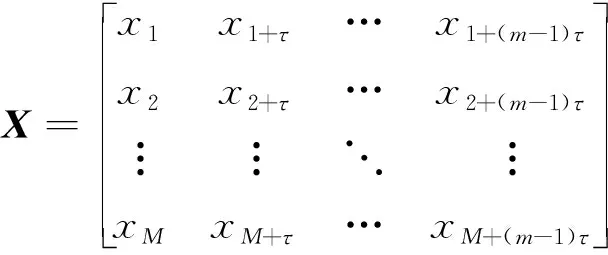
(1)

式中:τ为延迟时间;m为嵌入维数;M=N-(m-1)τ。

由式(1)可以看出,相空间轨迹完全由τ和m决定,因此正确地选取合适的τ和m具有十分重要的意义。本文采用互信息量法和G-P算法分别求取时间延迟τ和嵌入维数m。

1.1 互信息量法求时间延迟

两个变量X,Y状态数分别为s1和s2,其中X的信息熵为

(2)

式中:pi是X在状态i下出现的概率。

X和Y的联合熵为

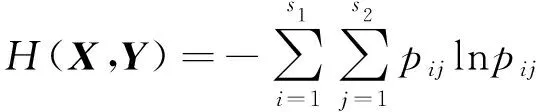
(3)

式中:pij是X在状态i且Y在状态j时出现的概率。

因此,X和Y两者的互信息为

I(X,Y)=H(X)+H(Y)-H(X,Y)

(4)

变压器振动信号xi经延迟时间τ后为xi+τ,这两者之间的互信息为

I(τ)=H(xi)+H(xi+τ)-H(xi,xi+τ)=

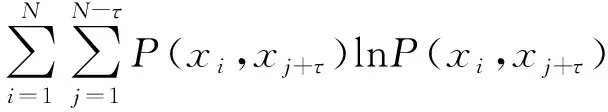
(5)

式中:H(xi)和H(xi+t)分别为xi和xi+t的信息熵;H(xi,xi+t)为xi和xi+t的联合信息熵。

变压器正常状态下振动信号的互信息量-延迟时间曲线如图1所示。

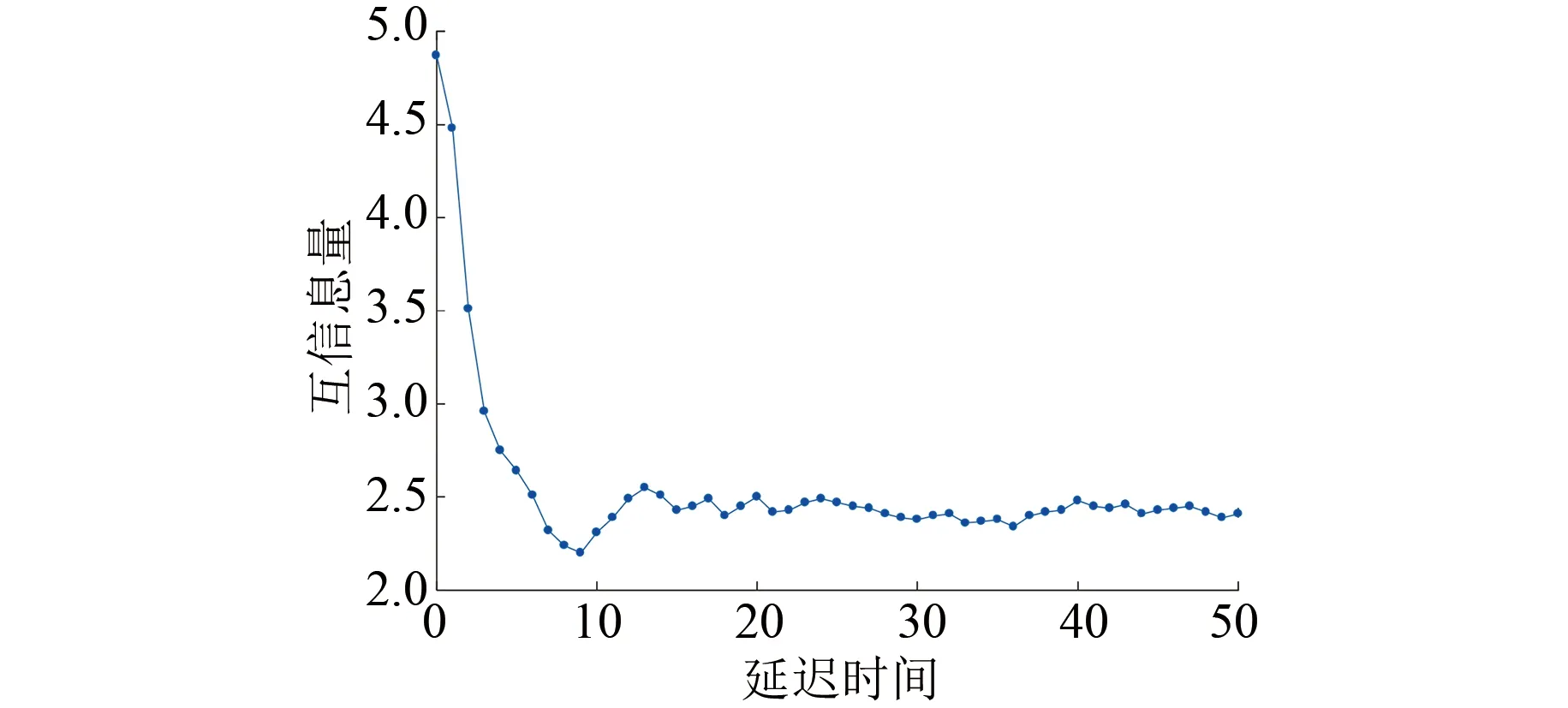
图1 变压器振动信号的互信息量-延迟时间曲线

由图1可知,通常将第一个极小值点对应的延迟时间作为最佳延迟时间,则此时的τ=9。

1.2 G-P算法求嵌入维数

定义引入时间序列的关联积分为

(6)

式中:|Y(xi)-Y(xj)|表示相空间中两点之间距离;r为一临界距离;q(x)为Heaviside函数。

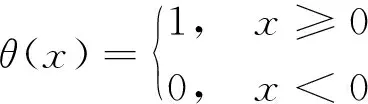
(7)

Cm(r)的含义为相空间轨迹中两点距离小于r的概率。在r的一定范围内,关联维数D(m)与Cm(r)存在对数线性关系,即

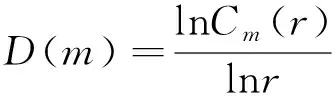
(8)

在获得了时间延迟τ的前提下,先选择一个较小的嵌入维数m0,此时可以求得对应的D(m0)。此后,不断增加嵌入维数,直到所计算的D(m)不再随m的增长发生明显变化为止,此时的m即为最佳嵌入维数。图2所示为变压器正常状态下振动信号的lnCm(r)随lnr变化的曲线。

图2 lnCm(r)随lnr变化的曲线

由图2可知,从m=3开始,lnCm(r)与lnr之间的线性关系部分基本不再发生变化,因此取m=3。

2 变压器绕组松动故障的混沌特征

在确定τ和m,重构出相空间的基础上,本文引入了关联维数、Kolmogorov熵和最大Lyapunov指数组成混沌特征,定量描述绕组处于不同状态下变压器振动信号的混沌特性。

2.1 关联维数

相空间轨迹是时间序列在相空间中经过多次靠拢、分离、来回拉伸与折叠形成的几何图形[16]。通过分形维数可以研究其形态特性,而关联维数作为一种分形维数,能够很好地描绘其动态特性。前文已介绍关联维数的计算方法,见式(8)。

2.2 Kolmogorov熵

Kolmogorov熵表征了系统运动的混乱程度。计算K熵一般用最大似然估计法和关联积分法,为方便起见,本文采用关联积分法求解K熵。其计算式如下:

(9)

2.3 最大Lyapunov指数

Lyapunov指数定量描述了两个很靠近的初值所产生的轨道,随时间推移按指数方式分离的现象[17]。其值反映了相空间轨迹的发散程度。通常只需求得最大Lyapunov指数lmax即可,并且该值能够作为判断系统是否具有混沌特性的判据:当lmax>0时,认为系统具有混沌特性。本文采用Wolf法求解最大Lyapunov指数,具体计算过程详见文献[18],此处不再赘述。

3 变压器模拟故障试验

为了获取变压器绕组松动故障下的振动信号,揭示其内部的混沌特性规律,本文搭建了变压器绕组松动故障模拟试验平台,如图3所示。试验器材包括:10 kV变压器一台;调压器一台;限流电阻三个;30 Mvar电抗器一台;30 Mvar电容器一台。

图3 故障模拟试验平台

由图3可知,220 V的工频电压经调压器升高到380 V,通过限流电阻输入10 kV变压器低压侧,高压侧并联接入30 Mvar电容器和电抗器,目的是模拟变压器带负载运行的现场情况。本试验变压器绕组松动故障设置方式为调节绕组螺母的预紧力,如图4所示。

图4 故障设置

由图4可知,本文设置了两种绕组松动故障,分别为绕组预紧力下降40%和80%。本文通过一台型号为DH5922的采集仪采集变压器顶部的振动信号,这是由于电力变压器的绕组通过紧固件与箱体顶部紧密接触,位于顶部的振动信号最为明显。采样频率为20 kHz。测点分布如图5所示。

图5 测点分布

4 试验结果与分析

本文以测点1的振动信号为例,在对其进行相空间重构以分析混沌特性之前,先计算其最大Lyapunov指数,用来判断其是否具有混沌特性,计算结果如表1所示。

表1 最大Lyapunov指数计算结果

由表1可知,根据绕组处于不同状态下的变压器振动信号计算出的最大Lyapunov指数均大于0,证明了其具有混沌特性,能够进行相空间重构进一步分析。变压器振动信号相空间重构情况如图6所示。

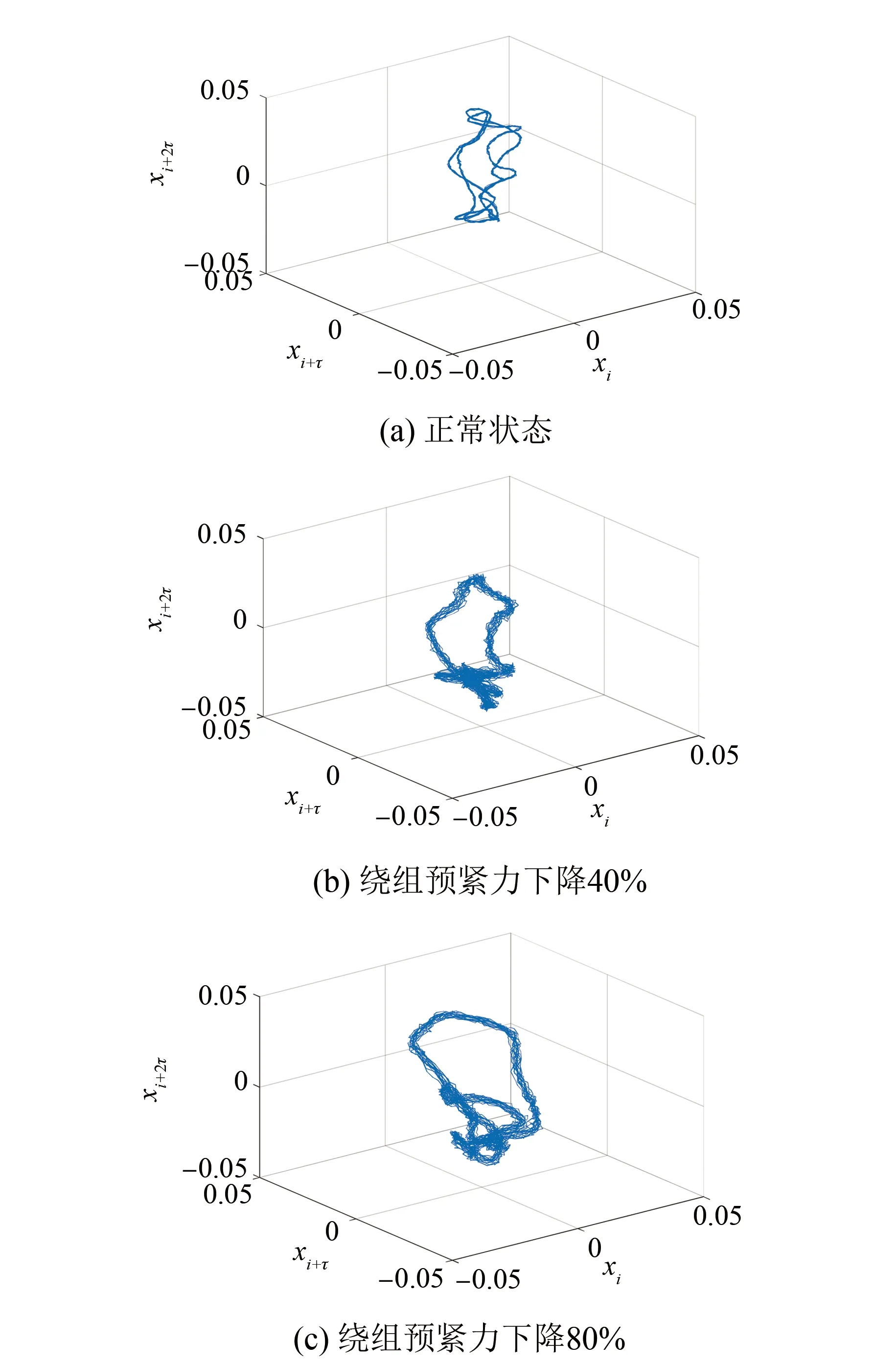
图6 绕组不同状态下的变压器振动信号相空间重构图

由图6可知,绕组处于正常、预紧力下降40%和预紧力下降80%状态的变压器振动信号嵌入维数均为3,延迟时间分别为9、11和13。由图6还可知,随着绕组松动故障的产生,变压器振动信号相空间轨迹分布情况也发生了变化,表明其混沌特性发生变化。具体变化规律为:随着绕组松动故障程度的加深,变压器振动信号相空间轨迹由正常时的闭合畸形椭圆状逐渐向外打开,且轨迹中间的混叠现象也随之减轻。

虽然相空间轨迹变化情况与绕组松动故障程度有关,但是为了提高现场应用性,本文选取关联维数、Kolmogorov熵和最大Lyapunov指数组成一组混沌特征定量表征其混沌特性。各个测点选取20组数据的计算结果平均值如表2～表4所示。

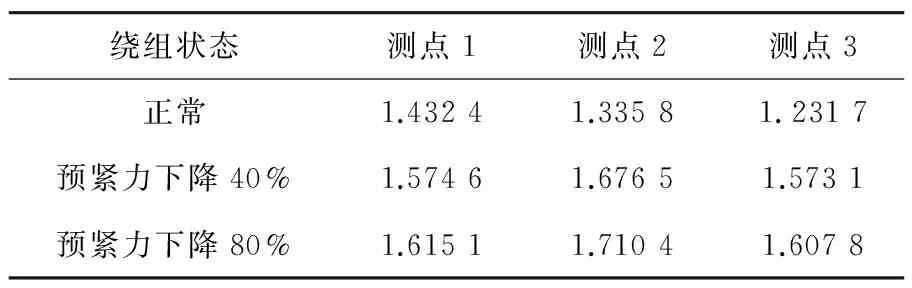
表2 各测点关联维数计算结果

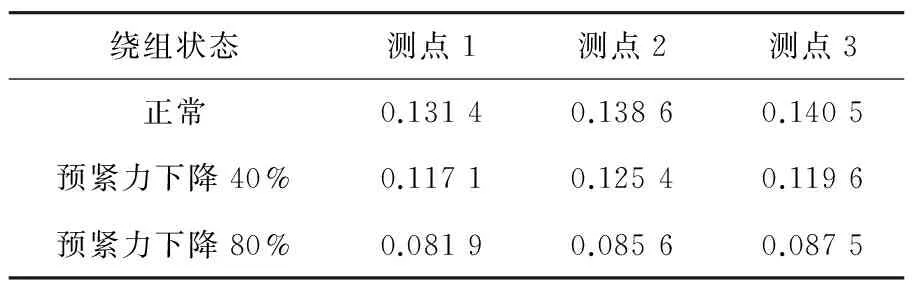
表3 各测点Kolmogorov熵计算结果

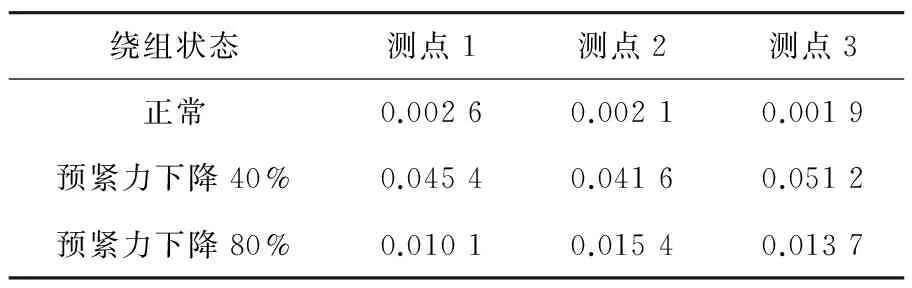
表4 各测点最大Lyapunov指数计算结果

由表2～表4可知,绕组处于不同状态下变压器振动信号同测点计算的关联维数、Kolmogorov熵和最大Lyapunov指数具有较好的区分度,能够定量描述对应相空间轨迹的混沌特性,在实际应用时可作为判据监测变压器绕组松动情况。

5 结 语

本文提出了一种变压器绕组松动故障的混沌特征分析方法。通过互信息量法和G-P算法分别求得延迟时间τ和嵌入维数m,证实了变压器振动信号在具有混沌特性的基础上对其进行相空间重构。然后分析其相空间轨迹随着绕组松动故障程度加深的变化规律,并引入关联维数、Kolmogorov熵和最大Lyapunov指数组成一组混沌特征定量表征绕组不同状态下的变压器振动信号的混沌特性。与时频分析法相比,该方法最大程度保留了原始信号的信息。结果表明,本文所提混沌特征分析方法适用于变压器绕组松动故障,能够有效地对变压器绕组松动故障进行监测与识别。