基于拓展矢量集的永磁同步电机模型预测控制

王德顺, 王开毅, 吕广宪, 谢宗楚

(1.东南大学 自动化学院,江苏 南京 210096;2.国网上海能源互联网研究院有限公司,上海 201210;3. 西南交通大学 电气工程学院,四川 成都 611756)

0 引 言

与异步电动机相比,永磁同步电机(PMSM)具有质量轻、效率高等优点,使得PMSM广泛应用于各个领域[1-3]。在PMSM的各种控制方法中,模型预测控制(MPC)因动态响应快及实现简单,吸引了工业界越来越多的关注[4-7]。MPC的控制策略最重要的特点就是在成本函数中包含非线性和系统约束。

传统的有限集模型预测电流控制(FCS-MPCC)在实际应用中会面临诸多挑战,如模型参数不匹配恶化控制效果、在线计算量大和需要较高的采样频率才能获得更好的控制性能等[8]。现有研究表明,在一个控制周期内应用多个电压矢量能有效提高控制性能[8-13]。在文献[9]中,所选有源电压矢量仅应用于一个控制周期的一部分,其余部分用零电压矢量填充,采用这种方法能显著提高低速性能。为了进一步提高控制性能,可以考虑两个非零电压矢量[11-12]或者三个电压矢量的组合[13]。在文献[14]中,证明了可以通过无差拍控制原理统一上述基于多个向量的FCS-MPCC。以上方法是通过改变采样频率调节系统来控制性能,这阻碍了FCS-MPCC的实际应用。

针对上述问题,通过对六个有源矢量进行占空比调制来增强控制集(CS),可以将更多具有占空比的向量作为候选向量。通过应用合成的电压矢量,可以获得更好的控制性能,而且可以通过调节CS的数量,实现在开关损耗和电流失真之间作出妥协,这更有利于FCS-MPCC在实际中的应用。

为方便控制性能和开关损耗的调节,本文提出了一种改进的拓展控制集预测电流控制(ECS-MPCC)算法。为了解决拓展控制集(ESC)数量增加造成的计算负担,本文设计了一种简化的最优电压矢量选择方法,可以将控制集候选电压矢量个数限制在11个以内,有效减小了控制器的计算负担,易于在低成本控制器上实现。

1 数学模型

以表贴式永磁同步电机为例,其在旋转dq坐标系下的数学模型表示如下:

(1)

式中:id、iq、ud、uq分别为dq轴电流和电压;Rs为电子电阻;Ls为电子电感;ωe为电角速度;ψr为转子永磁体磁链。

PMSM由两电平三相电压源逆变器驱动,逆变器共有8种不同的开关状态,其合成电压矢量如图1所示,候选电压矢量可描述为

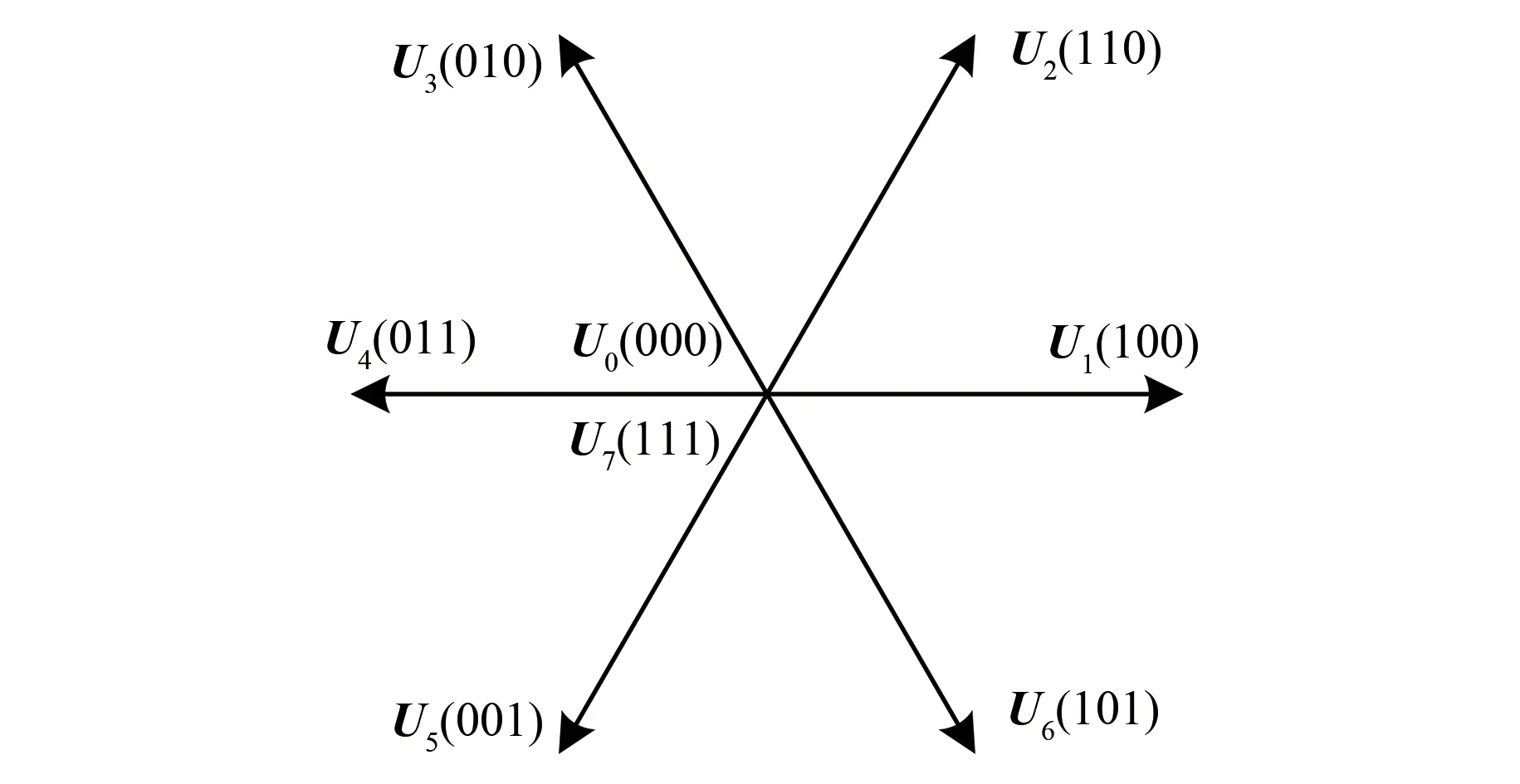
图1 基本电压矢量分布

(2)

式中:Uj(j=0,…,7)为8个基本电压矢量;Udc为直流母线电压;Sa、Sb、Sc分别为逆变器三个桥臂的开关状态。

2 ECS-MPCC算法

与通过开关状态使用固定电压矢量的传统FCS-MPCC不同,所提出的ECS-MPCC拓展了矢量集,能有效减小电流谐波。所提出ECS策略的虚拟电压矢量可以通过简单方程计算其值,考虑到枚举所有的电压矢量大大增加了实际系统的计算负担,针对该问题,提出了一种基于相邻矢量法缩减候选矢量个数,以降低算法的计算复杂度。

2.1 ECS电压矢量

所提出的拓展矢量集通过将基本电压矢量M等分和扇区矢量角N等分来获取,其电压矢量分布如图2所示。为了在没有任何查找表的情况下获得虚拟电压矢量值,所提出的方法通过使用图2每个电压矢量的坐标值获取,并定义为

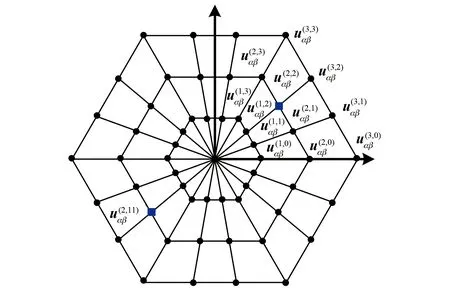
图2 所提出ESC的空间矢量分布(M=3, N=3)

(3)

式中:x、y分别为电压矢量对应的坐标值。

2.2 基于相邻矢量的候选矢量集

考虑到虚拟电压矢量会显著增加计算量,这将导致过多的硬件执行时间。因此,提出了一种基于相邻矢量的方法减少候选电压矢量。

通过欧拉法对式(1)进行离散化可以得到:

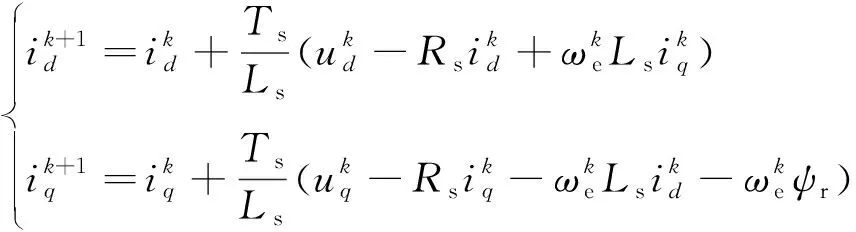
(4)

(5)

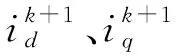
电流预测值可以用参考电流和电流波动表示:

(6)

考虑到稳态时,实际电流可跟踪参考电流,且在较小范围内波动。对于表贴式PMSM,一般采用idΔref=0的控制方式。因此,稳态时反电动势主要由q轴电流给定和转速决定,反电动势可近似为

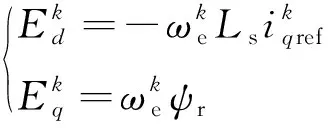
(7)

将式(6)和式(7)代入式(4),得到稳态时电压方程:

(8)

同理,k+1时刻的电压方程可以表示为

(9)

由于电机系统的机械时间常数远大于电气时间常数,可以认为电机转速在相邻几个控制周期内保持不变。根据式(8)和式(9),相邻控制周期的电压误差可以表示为

(10)

稳态时,d、q轴电流在参考值附近波动,所以有:

(11)

图3 候选电压矢量分布(区域S1)

图4 候选电压矢量分布(区域S2)

2.3 ESC-MPCC算法的候选矢量集

上述分析是基于稳态运行工况,并未考虑动态过程。针对非稳态运行工况,提出通过增加相反方向的待选矢量,以提高系统的动态响应速度。在速度闭环的FCS-MPCC算法中,速度外环采用PI控制器,PI控制器的输出作为转矩给定值。

本文采用表贴式PMSM,一般采用idref=0的控制方式,为了方便,通常将PI控制器的输出作为q轴电流参考值。三相PMSM的动态扰动主要来源于两部分:一是速度指令值变化;二是负载转矩变化。对于第一种情况,速度指令值变化只会改变内环MPC算法的输入iqref。对于第二种情况,当负载增大时,输出电磁转矩小于负载转矩,电机转速下降。由于速度指令值不变,给定速度与实际速度的误差为正,PI控制器的比例和积分环节输出增大,iqref增大,实际iq跟随iqref增大,输出电磁转矩增大,直到达到新的稳态。相反,当负载减小时,体现为iqref减小,实际电流iq跟随iqref减小,输出电磁转矩减小,直到达到新的稳态。因此,负载的变化对内环MPC的影响也是体现在电流给定值iqref的变化。

通过上述分析可以得知,系统的动态扰动最终体现在电流给定值iqref的变化。因此,只需要分析iqref突增或者突减情况下,FCS-MPCC算法的动态过程。

稳态时,忽略定子电阻压降,假设实际电流可以准确跟踪参考电流,则k时刻参考电压方程如式(12)所示。图5给出了稳态时,三相PMSM在αβ坐标系下的矢量关系图。

图5 稳态时的相量关系图

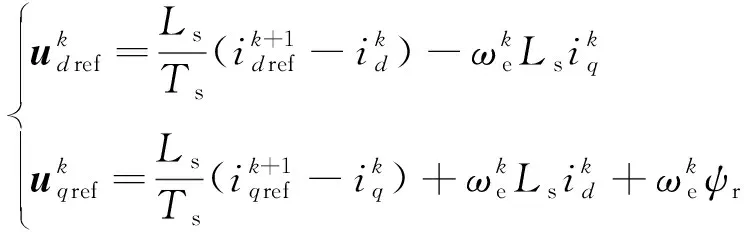
(12)

同理,可以得到k+1时刻参考电压为

(13)

图6 参考电流增大时的相量关系图

由式(13)可知,q轴电流增量表达式为

(14)

图7 参考电流减小时的相量关系图

(15)

(16)

当M≤2时:

(17)

当M>2时:

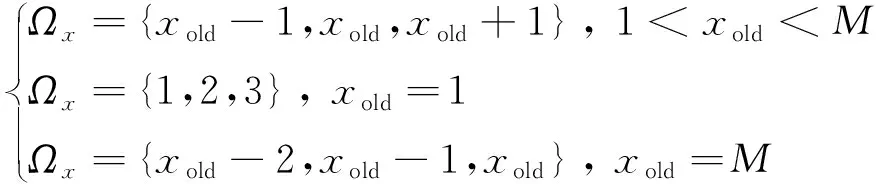
(18)

综上所述,当M=1时,控制集候选电压矢量个数为5个;当M=2时,控制集候选电压矢量个数为8个;当M>3时,控制集候选电压矢量个数为11个。通过相邻矢量的优化策略,可将ESC-MPCC算法控制集的候选电压矢量个数限制在11个以内。

3 仿真分析

为了验证本文所提的ECS-MPCC算法在不改变采样频率下,通过改变拓展矢量集大小来实现对控制性能和开关频率的调节效果,在MATLAB/Simulink搭建了控制系统的仿真模型。仿真所用电机的主要参数如表1所示,所用电机为表贴式永磁同步电机,所以有Ls=Ld=Lq。

表1 永磁同步电机参数

为了方便表述,将文献[6]中所提到的传统单矢量MPCC方法称为Method_tra;将文献[9]中所提的基于两矢量占空比MPCC方法称为Method_duty;将文献[15]中所提到的常规无差拍控制方法称为DPCC。本文所提方法在M=u,N=v时称为MethodMN_uv。

图8和图9分别是不同方法在转速100到600转时对应的相电流THD对比和平均开关频率对比。给定负载为10 N·m,控制频率为10 kHz。从图8和图9可知,当M=N=1时,所提方法MethodMN_11和Method_tra方法控制性能类似;当M=6,N=1时,所提方法MethodMN_61和Method_duty方法控制性能类似;当M=4,N=4时,所提方法MethodMN_44和Method_duty相比,相电流THD更低;与DPCC控制性能接近。

图8 不同方法的相电流THD对比

图9 不同方法的平均开关频率对比

综上所述,仿真结果表明,与Method_tra、Method_duty和DPCC方法通过调节采样频率改变控制性能不同,所提ESC-MPCC算法在固定采样频率下,可通过调节拓展矢量集大小选择不同的控制性能。

4 试验验证

为了验证所提出的ESC-MPCC算法的可行性和有效性,建立了一个试验平台,如图10所示。试验电机参数如表1所示,控制算法由TMS320F28335数字信号处理器实现。

图10 永磁同步电机驱动试验平台

4.1 稳态性能对比

为了评估所提方法的稳态性能,将其与Method_duty方法在600 r/min、10 N·m负载和10 kHz采样频率下进行了比较。

图11给出了两种算法在稳态运行时,a相电流波形及谐波分析。从图11可知,所提方法可以通过调节拓展矢量集来调节系统的控制性能,这和仿真分析结果一致。

图11 三种算法在稳态运行,a相电流波形及谐波分析

将稳态性能分析拓展到宽速域范围,对几种不同算法在不同速度下进行相电流THD和平均开关频率比较,如图12和图13所示。可以看出,在宽速域范围内,所提算法仅通过调节拓展矢量集大小,实现了系统开关损耗和相电流THD的动态调整。相比于传统MPCC,所提算法更利于在实际系统应用。

图12 不同算法在不同转速下,相电流THD对比

图13 不同算法在不同转速下,平均开关频率对比

4.2 动态性能对比

为了对比所提方法和Method_duty算法的动态响应性能,做了转速反转对比试验,如图14和图15所示。在转速反转试验中,永磁同步电机在空载下运行,转速由-600 r/min突变为600 r/min,1 s后转速突变为-600 r/min。从图14和图15可以看出,两种算法都可以快速响应并且有效跟踪参考电流,且响应时间都在1 ms左右。

图14 Method_duty算法转速反转试验波形

图15 MethodMN_44算法转速反转试验波形

5 结 语

针对传统有限集模型预测控制只能通过改变采样频率调节系统控制性能和平均开关损耗的问题。本文提出了一种用于永磁同步电机驱动的通用且简单的ESC-MPCC算法。所提算法不需要查找表,仅通过简单方程计算各候选电压矢量的值。为了不枚举所有候选电压矢量,提出了一种基于相邻矢量的方法缩减候选矢量个数,使ESC-MPCC算法的控制集候选矢量个数限制在11个以内。仿真和试验结果表明,所提算法与传统MPCC具有类似的动态性能,且可以在不改变采样频率情况下,仅通过调节拓展矢量集大小,满足控制系统对开关损耗和控制性能的不同要求。