基于分层COX模型的跟驰反应延迟时间生存分析

张彦宁，郭忠印*，高 坤，孙 智

(1.同济大学道路与交通工程教育部重点实验室，上海201804；2.中建山东投资有限公司,济南250101；3.中国建设基础设施有限公司,北京100044)

0 引 言

车辆跟驰(Car-following,CF)是基本微观驾驶行为之一，描述了同一车道中相邻两车之间的运动状态关系.研究者提出不同的车辆跟驰模型描述车辆跟驰.跟驰模型采用车辆运动状态历史值对当前值进行描述，历史值与当前值之间的时间间隔通常被定义为驾驶员的反应延迟时间[1]，例如经典的跟驰模型CA模型、Helly线性模型及AP模型等.反应延迟时间变量与驾驶员的感知时间和决策时间相关，是表示驾驶员跟驰行为的重要指标之一及微观跟驰模型中重要参数之一.一些研究者指出跟驰模型的仿真结果受到驾驶员反应延迟时间的显著影响，因此反应延迟时间应在模型中被重视[2-4].跟驰过程中的反应延迟时间包括生理延迟时间、机械延迟时间及运动延迟时间等.生理延迟时间是驾驶员反应时间，指驾驶员判断前车状态和采取对应驾驶策略的间隔时间，包括驾驶员的感知时间、识别时间、决定时间及动作反应时间，是跟驰行为的重要组成部分.反应延迟时间反映了后车对前车动作的反应灵敏度，影响微观驾驶行为变化规律与行驶风险[4].

研究表明，跟驰过程中驾驶员的反应延迟时间受车辆运动状态、驾驶员自身因素等影响[5-7]，并非经典跟驰模型中设定的定值[8].为优化跟驰模型，研究人员考虑反应延迟时间的可变性并对该参数建模.JURECKI R.[9]认为驾驶员的反应延迟时间受到车辆周边环境的显著影响，将加速、减速及变向等不同车辆运动状态下的反应延迟时间分开讨论.JURECKI R.认为驾驶员的反应延迟时间与跟驰距离线性相关，但没有量化车辆运动状态与反应延迟时间之间的关系.PEI X.[10]认为驾驶员反应延迟时间服从GAMMA 分布，通过考虑GAMMA分布的反应延迟时间获得了更好的模型稳定性.ARBABZADEH N.[8]通过分析自然驾驶数据发现驾驶员反应延迟时间取值范围为0.58～8.00 s，认为反应延迟时间与驾驶员自身因素之间存在显著关系.部分反应延迟时间研究中基于实测数据假设延迟时间分布类型[10]，没有考虑其他因素对延迟时间的影响，或者仅考虑驾驶员自身因素，忽略车辆运动状态与延迟时间之间的关系[8].

为弥补上述不足，本文采用生存分析方法分析车辆运动状态、光照条件与延迟时间分布间的关系.定义跟驰过程中驾驶员反应延迟时间，通过实车跟驰实验获取延迟时间生存数据并定义影响因素；基于Kaplan-Meier方法提出延迟时间单因素分析方法，构建分层COX 模型；最后，应用实验数据得出单因素分析方法及分层COX模型结果.

1 自然驾驶跟驰行为数据获取

1.1 延迟时间定义

延迟时间指前车行驶状态发生改变到后车行驶状态发生相应改变的时间间隔，包含后车驾驶员的感知、识别、决定及动作反应时间，表征后车受前车刺激后做出相应跟驰行为的全部过程.ZHANG[11]提出驾驶员延迟时间可通过前后车加、减速变化点识别，以前车加、减速变化点为延迟时间起点，后车加、减速变化点为终点，加、减速变化阈值为±0.15 m/s2.借鉴ZHANG[11]所提方法采集延迟时间，如图1所示.为避免特征点的误识别，在识别前使用局部加权平滑算法(RLOWESS)对原始数据进行预处理，以0.5 s为搜索时窗进行特征点识别.

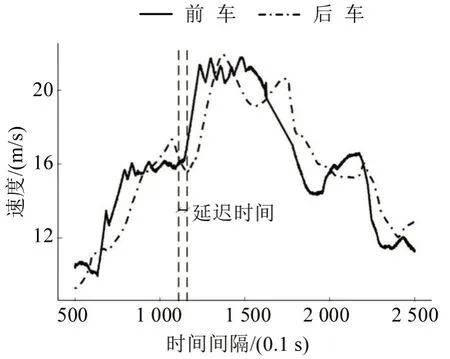
图1 延迟时间定义Fig.1 Definition of delay time

1.2 实车实验

(1)实验场地.

设计实车跟驰实验采集驾驶员跟驰过程中的反应延迟时间.跟驰实验的实验场地位于山东省S29 高速公路.实验路段为全封闭的高速路段，双向4车道，限速100 km/h，全场10 km.

(2)实验设备.

采用装载GPS、惯性导航系统的实验车辆进行前后车位置、速度及加速度的采集，数据的采样频率均为10 Hz.

(3)实验人员.

为减少驾驶员特性对实验结果的影响，本次实验选取20 名非职业的中青年驾驶员进行实验，驾驶员平均年龄30.4 岁，平均驾龄4.9年.在实验前将实验基本要求告知驾驶员，并进行预实验.

(4)实验步骤.

为获取驾驶员的反应延迟时间，驾驶员被要求跟驰前车行驶，前车由静止开始以20 km/h(5.6 m/s)为梯度加速至80 km/h(22.2 m/s)，并在每次加速后保持一段时间匀速行驶，随后以20 km/h为梯度减速至0 km/h，并在每次减速后保持一段时间匀速行驶.为研究反应延迟时间是否受光照条件影响，在白天、夜晚均进行了实验.

(5)数据处理.

对跟驰反应延迟时间进行采集并参考肖新平[12]对车头时距大于5 s 的跟驰数据进行筛除，共获取了266组延迟时间生存数据.

1.3 延迟时间影响因素定义

根据实验设计及实验数据定义光照条件、前车车速、前车加速度、前后车相对距离及前车加速度变化状态为延迟时间影响因素并赋值，如表1所示.前后车相对距离的定义参考BELLA F.[13]的研究，p0为前车加、减速超过阈值时前车的位置(m)，p1为后车位置(m).

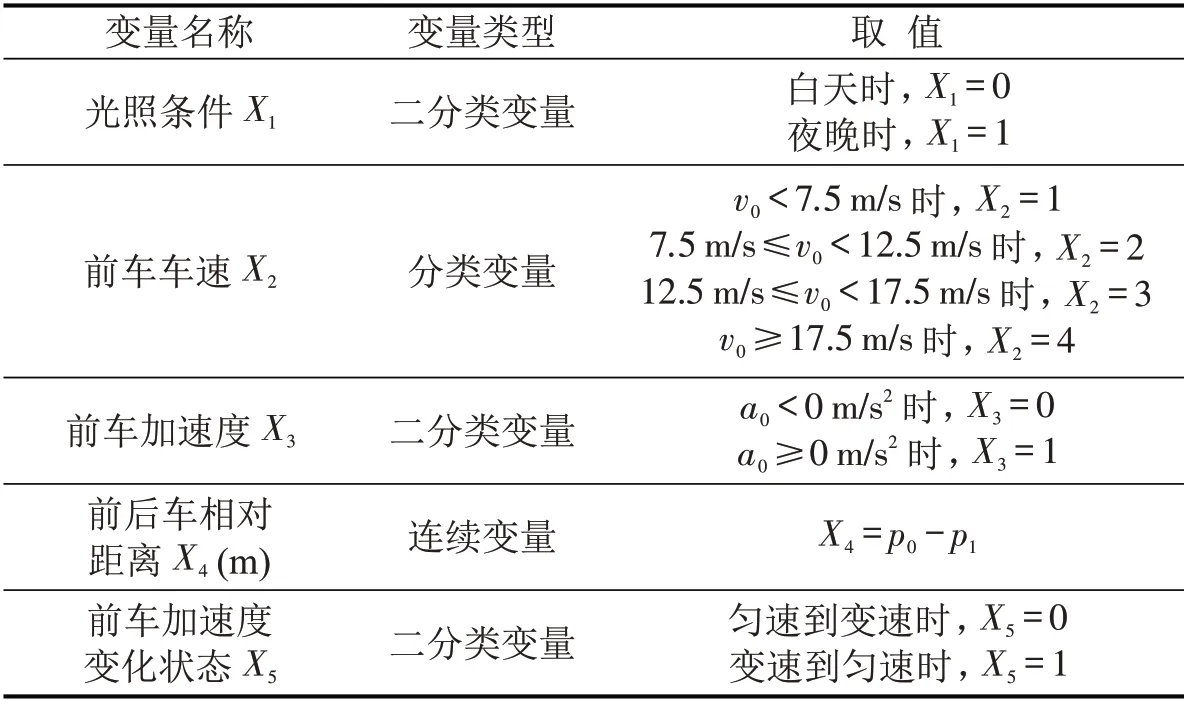
表1 延迟时间影响因素定义Table1 Delay time influencing factor definition

2 延迟时间生存分析模型

2.1 延迟时间生存分析要素

生存分析作为一种概率统计分析方法，用于分析以某一时间为起点、某一特定事件发生为终点的持续时间数据.根据生存分析的基本概念[14]，生存分析要素包含事件、事件生存时间t、事件结局δ、事件的生存函数S(t)及事件的风险函数h(t).

(1)事 件.

本文事件的起点时间为前车加、减速变化超过阈值的时刻，事件终点为后车加、减速变化超过识别阈值.

(2)事件生存时间.

事件生存时间t指由前车加、减速变化超过识别阈值到后车加、减速变化超过识别阈值的持续时间，即延迟时间.

(3)事件结局.

事件结局δ表示后车加、减速是否超过识别阈值，当后车加、减速超过识别阈值时认为事件失效，δ=1；当后车加、减速在整个观测时间内没有超过识别阈值时认为该条事件删失，δ=0.

(4)生存函数.

延迟时间的生存函数S(t)表示在前车加、减速超过识别阈值t时间后，后车加、减速还未超过识别阈值的概率，即

(5)风险函数.

事件的风险函数h(t)表明前车加、减速超过识别阈值后，t到t+Δt时间内后车加、减速超过识别阈值的瞬时概率，即

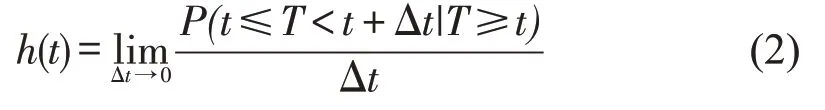
2.2 基于Kaplan-Meier的单因素分析方法

Kaplan-Meier 方法是一种估计生存函数的非参数方法，对Kaplan-Meier 估计的生存函数进行Log-rank 检验可分析单个因素对延迟时间生存曲线分布的影响.Kaplan-Meier 生存函数的计算方法为

式中：为延迟时间为tj时采用Kaplan-Meier方法估计的生存函数；tj为将延迟时间从小到大按顺序排列后的第j个值；(T ＞ti|T≥ti)为估计的当延迟时间达到tj且大于tj的概率.

逐一连接以延迟时间t为横坐标，生存函数S(t)为纵坐标的坐标点，可得到基于Kaplan-Meier估计方法的梯形生存曲线.Log-rank检验的原假设为两个不同生存曲线之间不存在显著性差异.Logrank检验的统计指标LRS计算方法为

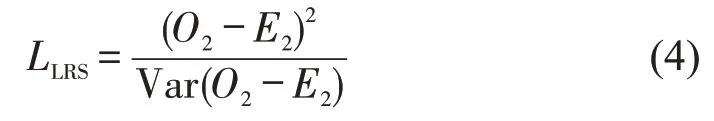
式中：O2为第2组生存数据的观察分数；E2为第2组生存数据的期望分数.

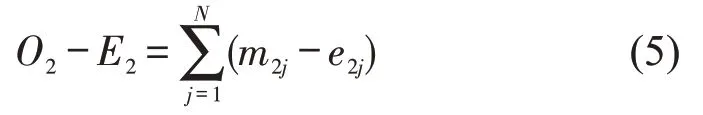
式中：m2j为第2 组生存数据在tj时，后车加、减速超过识别阈值的数量观察值；e2j为期望值；N为延迟时间按照从小到大排列后的总项数，即j∈[1,N].

2.3 PH假设与延迟时间分层COX模型

采用COX模型分析多个影响因素与延迟时间风险函数h(t)之间的关系.一般的COX模型形式为

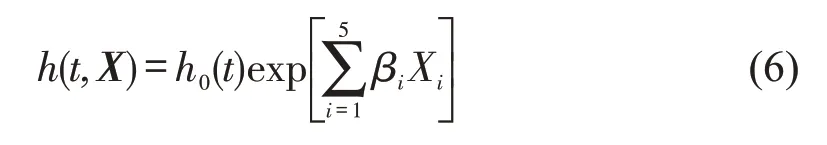
式中：X为延迟时间影响因素自变量Xi的向量，X=(X1,X2,…,X5)；βi为回 归系数，i=1,2,…,5 ；h0(t)为延迟时间的基准风险函数，h0(t)为非参数部分，通过生存数据估计.

在一般的COX 模型中，基准风险函数h0(t)随生存时间变化，βi为常数且与生存时间相互独立.对于复杂的生存数据，回归系数βi(t)可能随生存时间变化，为解决该问题通常采用分层COX 模型建模[14].在分层COX 模型构建过程中通过PH(Proportional Hazards)假设检验系数βi与生存时间之间的独立性.分层COX模型将不满足PH假设的p个自变量设置为具有k个分类的分层变量Z，对于Z的不同取值有不同的基准风险函数h0g(t)，g=1,2,…,k.PH 假设检验的统计量为Wald统计量或似然比统计量，原假设为回归系数βi与生存时间无关.延迟时间的分层COX模型为

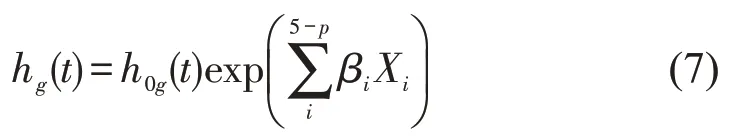
3 分析结果与讨论

3.1 延迟时间生存曲线单因素分析

基于延迟时间生存数据对分类变量进行Kaplan-Meier生存函数估计及Log-rank检验，相应结果如图2和表2所示.生存曲线结果表明：在夜晚跟驰行驶情况下，驾驶员的延迟时间比白天较短，log-rank 检验p=0.50，表明该差异不显著，如图2(a)所示；驾驶员延迟时间在低、中、高速行驶情况下差异不显著，p=0.80，如图2(b)所示；前车减速时驾驶员的延迟时间相比前车加速时短，p=0.00 表明该差异显著，如图2(c)所示；前车由匀速到变速运动时驾驶员的延迟时间相对较短，p=0.02 表明该差异显著，如图2(d)所示.单因素分析结果表明，驾驶员反应延迟时间受车辆运动状态影响，当匀速行驶的前车突然开始变速或前车相对后车开始减速运动时，驾驶员将做出迅速的反应.

3.2 延迟时间分层COX模型

采用COX模型分析多个因素与延迟时间风险函数h(t)之间的定量关系.首先，分析自变量的多重共线性，各自变量膨胀因子取值范围为1.156 2～1.688 8，变量间共线性风险小；随后，进行PH假设检验确定分层变量Z，结果如表3所示.假设检验结果表明，前车加速度变量对于延迟时间风险函数h(t)的影响随时间变化，不满足PH假设，故对延迟时间需构建分层COX模型，将前车加速度X3设置为分层变量Z，Z有k个取值，本文取k=2.

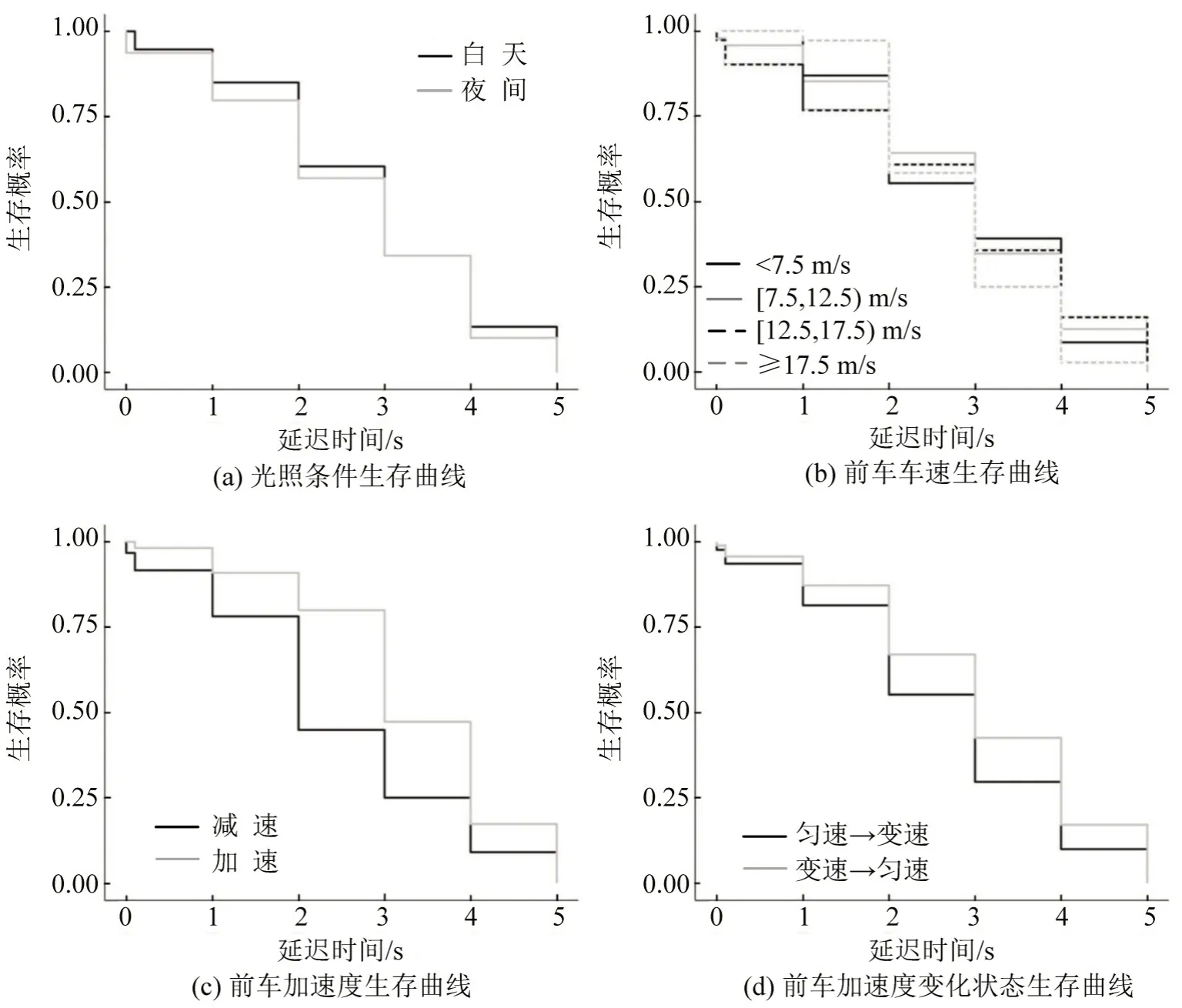
图2 基于Kaplan-Meier 的生存曲线Fig.2 Survival curve based on Kaplan-Meier method

表2 分类变量的log-rank 检验结果Table2 Log-rank test result of classified

延迟时间分层COX 模型参数估计结果如表4所示，生存函数如图3所示.前后车相对距离的回归系数为-0.006 2，风险比例为0.993 8，表明每当前后车相对距离增加1 m(10 m)时延迟时间风险函数h(t,X)减小0.62%(6.03%)，即后车加、减速在时间t超过识别阈值的概率减小0.62%(6.03%)，前后车相对距离越小驾驶员延迟时间越短.前车加速度变化状态回归系数为-0.436 8，风险比例为0.646 1，表明相比前车由匀速运动变为变速运动的情况，当前车由变速运动变为匀速运动时延迟时间的风险函数h(t,X)减小35.39%，即前车由匀速运动变为变速运动时驾驶员的延迟时间较短.分层COX模型的生存曲线(图3)表明，分层变量前车加速度对延迟时间的生存概率分布造成显著影响，当前车减速延迟时间较短，结论与单因素分析结论一致.分层COX模型结果表明，驾驶员反应延迟时间受车辆运动状态与车辆周边环境显著影响.

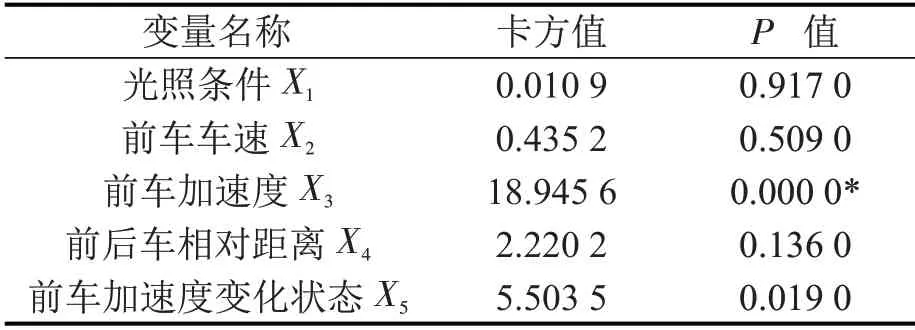
表3 PH 假设检验结果Table3 Test result of PH hypothesis

模型结果揭示了车辆加速度、加速度变化状态及跟驰距离与反应延迟时间间的定量关系.PEI X.[10]指出考虑反应延迟时间的可变性使跟驰模型仿真结果更加具有稳定性，结果更符合实际，此外CHEN J.[2]、ZHANG J.[3]也指出反应延迟时间显著影响微观交通仿真的结果.本文通过建模估计不同车辆运动状态、周边环境下的反应延迟时间，成果用于优化跟驰模型可使微观交通仿真结果符合实际情况并具有稳定性.

表4 延迟时间分层COX 模型参数估计结果Table4 Delay time stratified COX model parameter estimation result

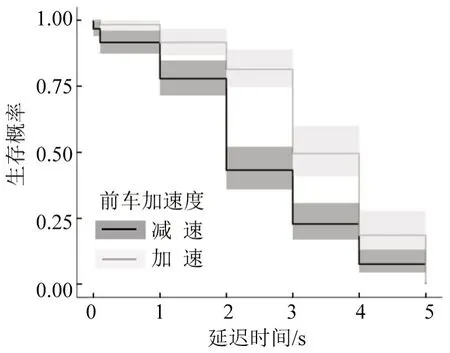
图3 延迟时间分层COX 模型生存曲线(95%置信区间)Fig.3 Delay time stratified COX model survival curve(95%confidence interval)

4 结 论

本研究基于自然驾驶行为数据，采用Kaplan-Meier 方法进行跟驰过程中驾驶员反应延迟时间的单因素分析，并采用分层COX 模型构建多个因素与延迟时间风险函数之间的定量关系.主要结论为：反应延迟时间的生存函数分布受前车加速度、前车加速度变化状态显著影响；前车加速度对反应延迟时间风险函数的影响随时间变化；当前后车相对距离增加1 m 时，延迟时间风险函数h(t,X)减小0.62%(6.03%)，当前车由变速运动变为匀速运动时，延迟时间的风险函数h(t,X)相比前车由匀速运动变为变速运动的情况减小35.39%.

研究结果从单因素和定量角度揭示了车辆运动状态、周边环境对驾驶员反应延迟时间的影响.通过模型估计不同情况下的反应延迟时间，为跟驰模型、微观交通仿真的优化提供理论基础.