基于路侧事故判别的公路平曲线车速限制研究

程国柱，程 瑞，徐 亮

(1.东北林业大学交通学院，哈尔滨150040；2.重庆交通大学重庆市交通运输工程重点实验室，重庆404100；3.长春工程学院土木工程学院，长春130012)

0 引 言

路侧事故定义为：车辆越过道路边缘或中心线，随后与护栏、电线杆、路侧行道树等固定物发生碰撞，甚至发生翻车、坠入深沟或河流的事故.根据美国联邦公路管理局调查统计，平均每年路侧事故占致死事故的50%以上[1].在中国，死亡人数超过3 人的交通事故中，路侧事故约占50%.相关研究显示，约有30%的路侧事故发生在小半径曲线路段[2].导致路侧事故的原因有很多，如驾驶人注意力分散、疲劳、饮酒、超速，路面湿滑、道路几何设计不良等.在众多路侧事故诱因中，超速是导致小半径曲线路段路侧事故频发的主要因素.

早期车速限制研究中，Fitzpatrick[3]等考虑圆曲线半径、竖曲线长度、纵坡及坡长、超高率等指标，构建了平纵组合线形的运行车速计算模型.程国柱[4]等通过建立高速公路驾驶人夜间识别距离模型与感知速度模型，给出高速公路夜间最高理论限速值与修正限速值的确定方法.Silva[5]等开展了道路特征及其与周围环境的交互作用研究，针对最高车速限制，建立了多项式Logit离散选择模型.

综上所述，国内外对车速限制已经开展了大量研究，但具体涉及到路侧事故最高车速的研究鲜见报道.为减少路侧事故率，基于仿真数据，利用路径分析方法筛选得到路侧事故显著性风险指标，计算得到各个风险指标对路侧事故的影响程度.借助贝叶斯判别方法构建路侧事故判别函数，提出对应不同道路设计指标的最高安全车速计算模型.研究成果可为公路曲线路段的车速限制提供参考，有助于减少路侧事故.

1 仿真试验

考虑到实车试验具有一定的高风险性，本文利用PC-crash 软件进行仿真试验.该软件广泛应用于交通事故再现和事故鉴定领域.通过对比真实事故数据与仿真数据，PC-crash软件获得的车辆碰撞数据具有较高的准确性和可信度，可作为开展路侧事故模拟和分析研究的有效工具[6].试验选取车速、车型、圆曲线半径、路肩宽度、纵坡坡度、超高横坡度、圆曲线加宽和路面附着系数8个风险指标作为影响变量，车辆最终行驶状态作为结果变量.车辆驶离行车道(包括车轮驶入路侧)表示路侧事故发生，如图1所示，车辆正常行驶表示路侧事故未发生.

图1 路侧事故发生Fig.1 Occurrence of roadside crashes

道路边坡坡度和路基高度是影响车辆驶入路侧后事故严重程度的主要因素，而对路侧事故是否发生没有影响，故在仿真软件中，建立行车道宽度为3.75 m的双向两车道弯道模型，并将边坡坡度设为1 ∶1 ，路基高度设为5 m.选择BMW-116d autom 和ASCHERSLEBEN KAROSS 作 为 小 型 客车和货车的代表车型，将车辆初始位置设定在单向行车道的中心处.当车辆行驶至弯道处，考虑驾驶人对车辆的转向控制和速度选择，在每次试验前对车速进行提前设置，针对不同圆曲线半径对车辆转向进行提前设定.根据《公路线形设计规范》JTG D20-2017 规定，当圆曲线半径不超过250 m时，才设置圆曲线加宽.各个变量的取值如表1所示.

表1 变量取值Table1 Value of variables

根据表1中圆曲线半径、路肩宽度、纵坡坡度、超高横坡度和路面附着系数的取值，构建5×4×4×4×4=1 280 种组合路段；通过对两类车型施加5 种初始速度，并根据不同圆曲线半径进行圆曲线加宽设置，共收集1 280×2×5=12 800组数据.

2 风险指标分析

2.1 路径分析原理

路径分析属于结构方程模型中的一种数据分析方法.利用路径分析不仅可以检验自变量对因变量的直接影响，还可以通过中介变量探讨自变量对因变量的间接影响，模型为

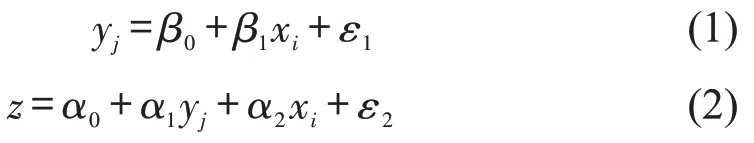
式中：ε1和ε2为随机误差；α0和β0为截距；α1，β1和α2为偏回归系数.式(1)表示变量xi首先将影响作用于中介变量yj的传递路径，式(2)表示变量xi对变量z的直接影响和通过中介变量yj对变量z的间接影响传递路径.

模型的偏回归系数表示各输入变量对结果变量的直接影响，但各输入变量的单位不同，不能直接反映其对结果变量的影响大小.为此，通过拟合二元Logistic回归模型，得到能够用于检验输入变量对结果变量直接影响大小的标准回归系数α′i，计算公式[7]为

式中：αi为变量xi的偏回归系数；Si为变量xi的标准差；SZ为Logistic 回归模型中随机变量Z的标准差，取

变量xi通过中介变量yj对变量z的间接影响γi为

式中：βij为变量xi与中介变量yj之间的相关系数；α′j为中介变量yj的标准回归系数；n为中介变量yj的数量,j=1,2,…,n.

由式(3)和式(4)可得到变量xi对变量z的总体影响χi，计算公式为

2.2 显著性风险指标筛选

将仿真数据纳入Logistic回归分析中，初步分析结果如表2所示.表2显示，圆曲线加宽所对应的p值大于0.05(显著性水平)，无统计学意义，即圆曲线加宽对路侧事故发生影响不显著，在模型中予以剔除.

表2 模型结果Table2 Results of model

2.3 风险指标影响程度分析

将上述显著性风险指标继续纳入Logistic 回归分析中，可以得到偏回归系数和标准差，利用式(3)求得各个风险指标对应的标准回归系数，即对路侧事故的直接影响大小，如表3所示.由此得到各个风险指标对路侧事故的直接影响程度由大到小依次为：车速、圆曲线半径、车型、路面附着系数、路肩宽度、纵坡坡度和超高横坡度.

表3 直接影响Table3 Direct effect

根据模型中各个风险指标间相关系数及对路侧事故的直接影响，利用式(4)求得各个风险指标通过其他指标对路侧事故的间接影响，如表4所示.根据路径分析结果可知，车速通过圆曲线半径对路侧事故的间接影响最大，为2.292；圆曲线半径通过车速对事故的间接影响最大，为-2.960.其他所有指标也通过车速和圆曲线半径对路侧事故产生了最大和第二大间接影响.由此可得，车速和圆曲线半径是造成路侧事故的主要危险指标.表4还给出了各个风险指标对路侧事故的总体影响，按照总体影响由大到小依次为：车速、圆曲线半径、车型、路面附着系数、路肩宽度、纵坡坡度和超高横坡度.值得注意的是，与直接影响相比，这些风险指标的重要性顺序并未改变，这表明不同风险指标的间接影响在决定路侧事故发生方面并未发挥重要作用.

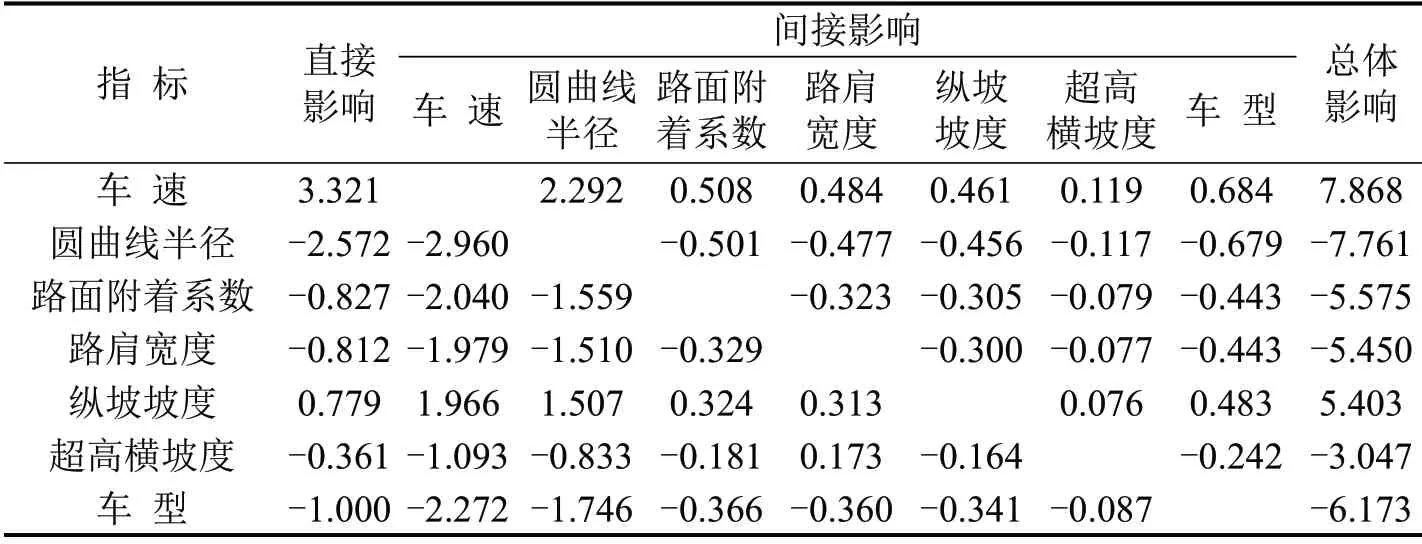
表4 路径分析结果Table4 Results of path analysis

3 最高安全车速

3.1 贝叶斯判别原理

贝叶斯判别理论方法是建立在研究对象被分成若干类别或已知类别数目的基础上，从大量数据样本中总结出判别规则，建立准确有效的判别函数，进而对未知所属类别的研究对象进行分类的过程.

设A1，A2，A3，…，Am为m个类别，对应的概率密度函数分别为：f1(x)，f2(x)，…，fm(x).假设这m个类别出现的先验概率为p1(x)，p2(x)，…，pm(x).当对一个样本数据x进行分类判别时，利用贝叶斯概率公式可计算x来自第i个类别的后验概率为

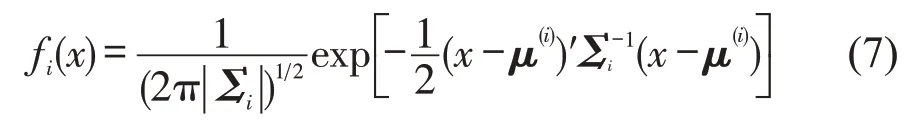
式中：μ(i)为第i类别的均值向量；Σi为第i类别的协方差矩阵.

贝叶斯判别的目的在于找到样本数据x的所属类别i，使得P(i/x)最大.由式(6)可知，不同类别的P(i/x)值主要取决于分子部分，即P(i/x)f(x)，而与分母部分无关.因此可改为求解令P(i/x)f(x)最大化的i.对式(7)两边同乘以pi(x)，并对其取对数，去掉与i无关项，化简后得到等价判别函数为

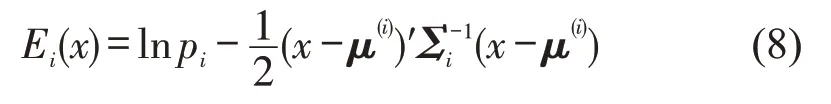
3.2 路侧事故判别模型

本文研究的路侧事故状态包括发生和不发生两种状态，即：当事故发生时，i=1；事故不发生时，i=2.由2.3 节可知，车型对路侧事故影响较大，为探究不同车型所对应的路侧事故判别条件，针对小型客车和货车分别构建路侧事故判别函数.将车速、圆曲线半径、路面附着系数、路肩宽度、纵坡坡度和超高横坡度作为自变量，路侧事故状态作为分类变量，纳入贝叶斯判别分析中.部分仿真数据可能存在不符合多元正态分布情况，故采用逐步判别方法进行分析.由此得到小型客车和货车的判别函数检验结果如表5所示.

表5 检验结果Table5 Test results

由表5可知，小型客车和货车检验结果中Wilks 的最终Lambda 值分别为0.008、0.005，且所有Sig 值均等于0.000，具有统计学意义.说明无论对于小型客车还是货车，上述6个被纳入贝叶斯判别分析的风险指标对判别函数均具有较高的显著性.因此，采用这6个风险指标建立的判别函数，具备较强的判别能力.由此构建的路侧事故判别函数如下：

(1)小型客车.

路侧事故发生判别函数为

路侧事故不发生判别函数为

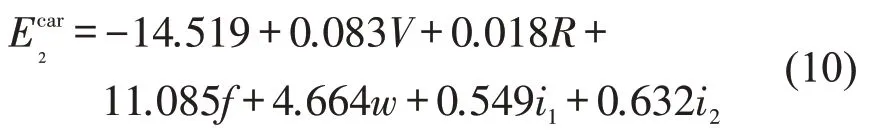
(2)货 车.

路侧事故发生判别函数为

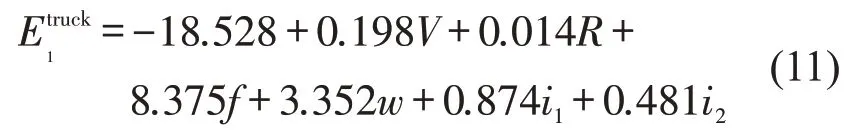
路侧事故不发生判别函数为

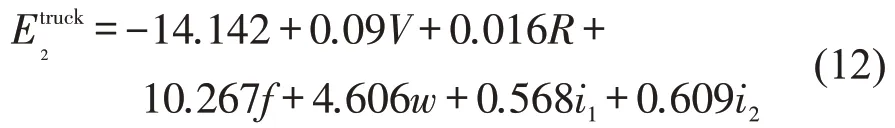
式中：为小型客车发生路侧事故的判别函数值；为小型客车不发生路侧事故的判别函数值；为货车发生路侧事故的判别函数值；为货车不发生路侧事故的判别函数值；V为车速(km/h)；R为圆曲线半径(m)；f为路面附着系数；w为路肩宽度(m)；i1为纵坡坡度(%)，下坡为正，上坡为负；i2为超高横坡度(%)，外侧超高为正，内侧超高为负.

将一组风险指标带入式(9)～式(12)中，若得到的函数值E1＞E2，则判定为发生路侧事故；若E1＜E2，则判定为不会发生路侧事故.

3.3 最高安全车速计算模型

通过路径分析可得，车速是造成路侧事故的最危险指标.故在难以对道路线形进行优化设计的情况下，需要对车速进行有效控制.基于构建的路侧事故判别函数，当E1＞E2，才会发生路侧事故.故在此基础上，分别令及，通过联立判别函数式(9)和式(10)，以及判别函数式(11)和式(12)，整理化简后，可得到对应不同道路线形指标和路面条件的小型客车和货车的最高安全车速临界值计算模型，分别为

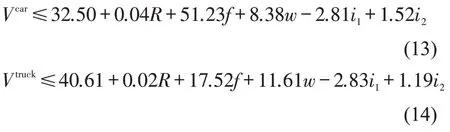
式中：Vcar为小型客车最高安全车速临界值(km/h)；Vtruck为货车最高安全车速临界值(km/h).

3.4 模型验证

为证实所构建最高安全车速计算模型的有效性，选取一起真实事故案例进行验证.

2018年5月20日，一辆小型客车行驶至事故地点驶入路侧沟渠.根据警方材料及现场勘查可知，事发路段为干燥沥青路面，圆曲线半径为32 m，路肩宽度为1 m，纵坡坡度为0，路拱横坡度为0.5%，路面附着系数为0.7.事故概况如图2所示.

将事发路段道路设计指标代入式(13)中，计算得到此路段所能允许的小型客车最高安全车速为

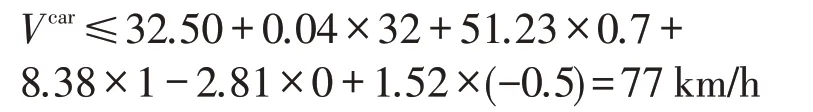
图2 事故概况Fig.2 Accident scene

根据计算结果，若小型客车以大于77 km/h的速度通过上述路段，则判定会发生路侧事故.结合事发路段监控视频，运用视频图像法计算得到小型客车事故时，车速约为83 km/h，大于77 km/h，由此验证了最高安全车速计算模型的准确性.

4 案例应用

国道G105 线中山沙朗—古鹤段改建工程采用设计速度80 km/h的一级公路技术标准.根据设计安评结果可知，项目存在多处小半径曲线路段，故有必要进行车速限制.根据工程经验可知，小型客车轮胎与路面的附着系数一般取0.7，货车轮胎与路面的附着系数一般取0.6.利用构建的最高安全车速计算模型，根据道路线形设计资料，计算得到对应不同车型的小半径曲线路段的最高车速限制值，如表6所示.

表6 最高安全车速Table6 Maximum safe speed

从表6可以看出，路侧事故最高安全限速值与线形条件密切相关，总体特点是道路线形条件越好，限速值越大.在相同线形设计指标下，小型客车最高限速值均大于货车最高限速值，这与实际工程经验相符.计算得到：小型客车的最大限速值为98 km/h，最小限速值为86 km/h；货车的最大限速值为93 km/h，最小限速值为81 km/h.

5 结 论

基于Logistic回归模型的路径分析方法，筛选得到路侧事故显著性风险指标，分析其对路侧事故的影响程度大小.根据贝叶斯判别分析方法，分别构建了对应不同车型的路侧事故判别函数.最后，提出一种对应不同圆曲线半径、路面附着系数、路肩宽度、纵坡坡度和超高横坡度的最高安全车速计算模型，利用事故案例验证了其有效性，并予以实例应用.