甄选正余弦定理 优化解题方法

龙成芳

(贵州省天柱民族中学)

正弦定理和余弦定理是解三角形的有力工具,也是高考的必考知识点.针对正弦定理和余弦定理的应用进行分析和总结,可以将题型分为已知三角形的部分边和角解三角形、给出三角形的边角关系解三角形两种类型.在解题过程中,有些题目只能使用正弦定理,有些只能使用余弦定理,还有一些可以同时使用正弦定理和余弦定理,也有些题目要先使用正弦定理后使用余弦定理,或者先使用余弦定理再使用正弦定理.解题关键在于恰当选择解题方法,不同的选择会导致解题难度的不同,甚至可能无法得到准确的结果.因此,本文通过具体分析,指出什么情况下应使用正弦定理,什么情况下应使用余弦定理,这将有助于学生在解决类似问题时选择合适的方法.

1 已知三角形的部分边和角

当前的问题类型涉及正弦定理和余弦定理的直接应用,属于基础问题.这些问题可分为以下几种情况:已知两个角(或三个角)和一条边、已知两条边和一个角、已知三条边、多个三角形拼接等.接下来对每种情况进行详细分析.这种分类方式有助于解题者更好地理解问题,并根据给定信息选择适当的解题方法.

1.1 已知两角一边

例1 (2015年安徽卷文12)在△ABC中,AB＝,A＝75°,B＝45°,则AC＝.

因为A＝75°,B＝45°,所以C＝60°,又AB＝,由正弦定理得,则AC＝2.

对于本题,已知三角形的两个角和一条边,选择使用正弦定理来解决问题.尽管该题也可以使用余弦定理来进行求解,但这种方法相对更复杂,需要联立方程组并进行较多的计算.因此,本类型题通过运用正弦定理来求解,可以更简捷地得到正确答案.

1.2 已知两边一角

例2 (2021年全国甲卷文8)在△ABC中,已知

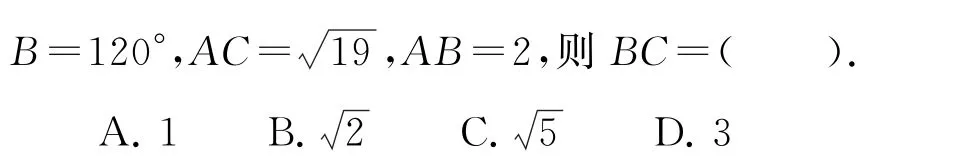
在△ABC中,因 为B＝120°,AC＝,AB＝2,所以由余弦定理得

即19＝22＋BC2＋2BC,即BC2＋2BC－15＝0,解得BC＝3,故选D.

根据题目已知条件,本题选择采用余弦定理求解,但是在已知两边一角的题型中,要分成两类,即一类是已知的角是其中已知一边的对角,若要求第三边,则直接用余弦定理,若要求角则先用正弦定理求出已知的另外一边所对的角比较简单一些;另一类是已知两边及夹角,不管先求第三边还是求角,这种情况先用余弦定理求出第三边比较简单,在解题过程中应注意识别题型.

1.3 已知三边

对本题,已知三角形的三条边,选择直接使用余弦定理来解决问题.这种情况是典型的余弦定理应用问题.通过使用余弦定理,我们可以计算出三角形的任意一个角.因此,在已知三角形的三条边的情况下,直接使用余弦定理是最恰当的方法.

1.4 多个三角形拼接

多个三角形拼接问题可以看作前面提到的几种情况的综合应用.解决这类问题的关键是要先识别各个部分三角形属于以上三类中的哪一类,这是解题的突破口.通过对各个部分三角形进行分类,可以应用相应的方法进行求解.

例4 如图1 所示,在△ABC中,角A,B,C所 对的边分别为a,b,c,已知a＝3,c＝,B＝45°.在边BC上取一点D,使得求tan∠DAC的值.

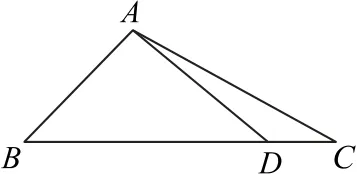
图1

该题属于多个三角形拼接的情况,解题的关键在于采用适当的解题思路.首先,我们需要“两明确”,即明确要求量所在的三角形,并确定在这个三角形中需要求解的是什么.其次,要明确哪个三角形是完全可以解的,即该三角形中已知的元素符合“两角一边”“两边一角”或“三边”的情况.接下来,借助可解的三角形,求出需要求解量所需要的相关元素.最后,根据解三角形的方法,求出要求的量.

有的实际应用问题也可以看作多个三角形的拼接问题,只是结合了一些具体的物理量或生活情境.通过数学建模将实际应用问题转化为数学问题,解题思路和方法与该类型题目相同.因此,解决实际应用问题的关键也是将问题进行拆解,找出可解的三角形,并依据相应的解题思路求解所需的量.

2 已知三角形的边角关系情况

在高考中,解三角形的一种常考题型是已知三角形中的一个或多个边角关系式,然后在已知的基础上解该三角形.这类题型主要考查正弦定理和余弦定理,通过对这种题型进行梳理总结发现,三角形的边角关系方程大致可以分为三类:一是已知三角形三条边的齐次方程,如a2＋b2＝3ac,或者是关于角的正弦函数的齐次方程,如sinA＋2sinB＝5sinC;二是已知方程中有三角形角的余弦函数,没有三角形边的齐次,如a＋b＝cosC;三是方程中既有边的齐次式,又有角的余弦函数,如a2＋b2＝accosB.下面结合实际题目,从可以用正弦定理、可以用余弦定理和既可以用正弦定理又可以用余弦定理三种情况进行一一分析.

2.1 用正弦定理的情况

例5 (2023年全国乙卷文4)在△ABC中,内角A,B,C所对的边分别为a,b,c,若acosB－bcosA＝c,且,则B＝( ).

因为acosB－bcosA＝c,由正弦定理得sinAcosB－sinBcosA＝sinC,又 在△ABC中,因为C＝π－A－B,所以

以上两个例题,分别体现两种可以先用正弦定理处理的情况.通过以上两个例题发现,这类问题也不是想象的那样复杂,关键是看清楚已知:一是题目给出边的齐次方程(但形如a2＋b2－c2＝nab(－2＜n＜2),a2＋c2－b2＝nac(－2＜n＜2)或b2＋c2－a2＝nbc(－2＜n＜2)的除外)可以先用正弦定理对等式进行处理;二是题目给出角的正弦函数的齐次方程,则选择先用正弦定理对方程进行处理,一定要注意是“齐次”方程,否则不能用正弦定理.

2.2 用余弦定理的情况

已知方程中有边但不齐次,且有角的余弦函数,如a＋b＝cosC,除非告知三角形的外接圆半径,要不然很明显是不能先用正弦定理的,所以在对这类问题进行处理时,应该先用余弦定理将角化为边,再进行运算.当然,还有一种必须弄清楚的是关系式也是边的齐次方程,形如a2＋b2－c2＝nab(－2＜n＜2),a2＋c2－b2＝nac(－2＜n＜2),或b2＋c2－a2＝nbc(－2＜n＜2),以及以上三种的变形形式,很像余弦定理的形式,这种虽然是三角形的边的齐次方程,但用余弦定理更直接.

例7、例8均是先用余弦定理,其实仔细观察可以发现:例7是已知给出的等式不是三角形边的齐次方程,也不是角的正弦函数的齐次方程,但是方程中含有三角形的角的余弦函数;例8是给出三角形的边的齐次,且均为二次方程,但是形如余弦定理形式,特别b2＋c2－a2是余弦定理的部分,可以先用余弦定理解决问题,故解题中先用余弦定理的两种情况:一是题目出现三角形的角的余弦函数的方程;二是出现形如及变形形式的方程.

2.3 既可以用余弦定理,又可以用正弦定理的情况

根据前面情况综合,既可以用余弦定理,又可以用正弦定理的题型是所给的三角形边角关系等式中,既是边的齐次方程又含角的余弦函数,如c＋b＝acosC,则这种题可以先用正弦定理,也可以先用余弦定理.

例9 (2021年北京卷17,节选)已知在△ABC中,c＝2bcosB,,求B.

根据例9可知,既可以用正弦定理又可以用余弦定理求解的题型非常明确,即题目中给出的已知条件既有边的齐次,又有角的余弦函数的方程或形如及变形形式时,用正弦定理和余弦定理均可,只是选择的方法不一样,路径就不一样,难易程度也就不一样.本人认为能用正弦定理的情况,可以优先考虑正弦定理,因为正弦定理比余弦定理计算量小一些,可以减少计算导致的失误.

本文主要针对正弦定理和余弦定理展开探索,对什么情况下用正弦定理、什么情况下用余弦定理进行了具体的分析总结.已知三角形三个元素解三角形,这种题型主要分四种情况:

一是已知两角(三角)一边,利用正弦定理解三角形;

二是已知两边及夹角,利用余弦定理解三角形;

三是已知三边,利用余弦定理解三角形;

四是已知两边及其中一边的对角,这种情况要看问题求什么,若要求角,则用正弦定理,若要求第三边,则用余弦定理.

已知三角形的边角关系的情况,当题目中出现给出三角形边的齐次方程、三角形角的正弦函数的齐次方程这两种情况时,选择先用正弦定理.当出现给出三角形的角的余弦函数的方程、形如及变形形式的方程时,选择先用余弦定理;当既有边的齐次或角的正弦函数的齐次,又有角的余弦函数或形如及变形形式的方程时,既可以用正弦定理也可以用余弦定理.

在解题过程中,用正弦定理还是余弦定理,本文对各种情况均进行了明确的分析说明,在解题中只要对照情况进行分析就可以明确正弦定理和余弦定理的使用情况,这能大大节省时间,优化解题方法.

(完)