强基计划数学备考中的三角求值问题

张欣然

(北京中学)

1 知识补充

1)半角公式:

2)万能公式:

3)三倍角公式:

4)积化和差与和差化积公式:

a)积化和差公式:

b)和差化积公式:

2 技巧归纳

三角函数的求值与化简:

1)对于常用的三角函数的相关公式要熟练掌握,争取达到“内化于心”的程度.

2)熟悉三角恒等变换的一般原则.

a)角少:尽可能用较少的已知角去表示未知角;

b)名少:尽可能用较少的三角函数表达其余三角函数;

c)次数低:面对高次式,要用降次公式对其降次处理;

d)用好1:要熟悉1 的一些特殊代换,如1＝tan45°＝sin2α＋cos2α,1＋cos2α＝2cos2α等.

3 经典例题

例1 (2017年北京大学)9tan10°＋2tan20°＋4tan40°－tan80°＝( ).

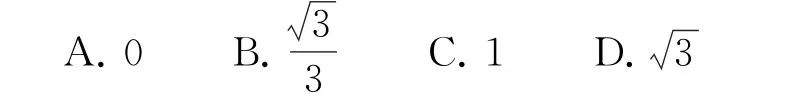
分析 注意到题中出现的角依次为2倍关系,可联想到正切的2倍角公式,再注意到是求和,可考虑裂项相加法.

将以上三式相加得

所以9tan10°＋2tan20°＋4tan40°－tan80°＝0,故选A.

推广 tanθ＋2tan2θ＋…＋2ntan2nθ＝cotθ－2n＋1cot2n＋1θ.

例2 (2016年清华大学,多选题)已知α＝1°,β＝61°,γ＝121°,则( ).

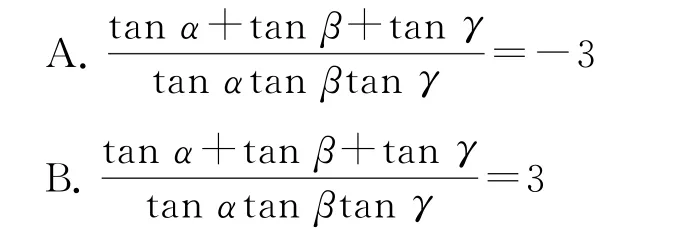
C.tanαtanβ＋tanβtanγ＋tanγtanα＝－3

D.tanαtanβ＋tanβtanγ＋tanγtanα＝3

分析 注意观察角的联系,发现可考虑正切的差角公式求解,易知C 正确,则D 错误.但本题是多选题,那么选项A 和B又如何研究呢? 事实上只需将分式的分母除到分子里,即可发现A 和B反映的是余切两两乘积的和,再注意到正切和余切的倒数关系不难求解.或者直接推导出两角差的余切公式,再结合角的关系使问题获解.

或“感性”分析一下:注意到tanα＞0,tanβ＞0,tanγ＜0,且|tanβ|＞|tanγ|,结合诱导公式可知B错误,则A 正确.

可得

同理,有

将①②③相 加 可 得tanαtanβ＋tanβtanγ＋tanγtanα＝－3,故C正确.

再由①②③可得

统计比较两组患儿的治疗效果、止吐时间、止泻时间以及退热时间。患儿治疗后各种临床症状得到显著的改善,大便次数相较治疗前明显减少,视为显效;患儿治疗后各种临床症状有所改善,大便次数有所减少,视为有效;患儿治疗后各种临床症状没有得到改善,大便次数也没有变化,视为无效。

将以上三式相加得

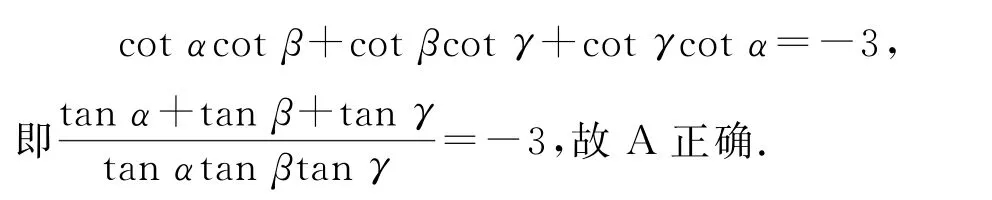
综上,选AC.

解法2 tan(β－60°)tanβtan(β＋60°)＝

所以

则A 正确.

所以C正确.

综上,选AC.

推广 若β－α＝60°,γ－β＝60°,则

解法1 注意到

故选D.

解法2

A.0 B.1

C.无穷多个 D.前三个答案都不对

解 化解得

下面需要对这个式子进行估算,注意到

例6 (2010 年 清 华 大 学)求 值:sin410°＋sin450°＋sin470°.

分析 本题次数较高,要先用降幂公式对所求解析式中的四次方进行多次降次,再化简求解.

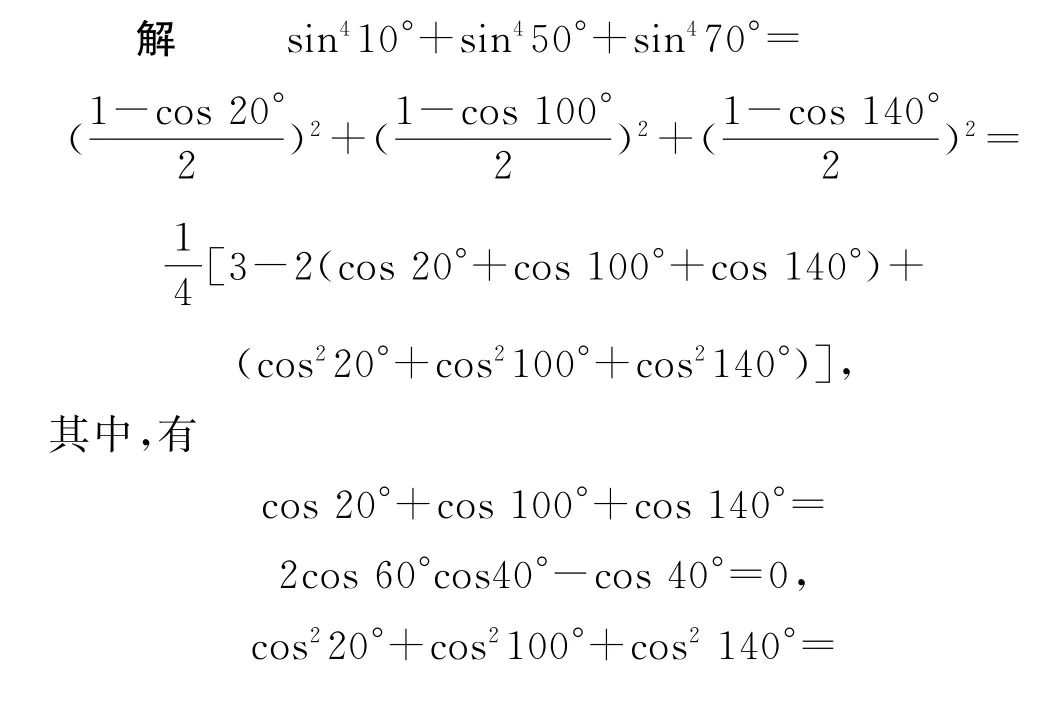
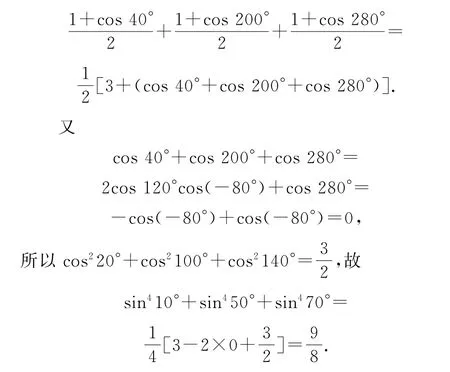
遇到高次数就考虑进行降次,遇到角或函数名的差异就考虑缩减这种差异,遇到常数1就要想到把其换成三角值,这些是我们在三角函数化简与求值时要秉承的基本原则.

例7 求sin18°的值.

解法1 由sin36°＝cos54°,可得

因为cos18°≠0,所以4sin218°＋2sin18°－1＝0,因为sin18°＞0,所以

解法2 由cos36°＝sin54°,可得

分解因式得

因为sin18°≠1,所以4sin218°＋2sin18°－1＝0.下同解法1.

解法3 构造等腰△OAB,使顶角∠AOB＝36°,OA＝OB＝1,作∠OAB的平分线AD,则

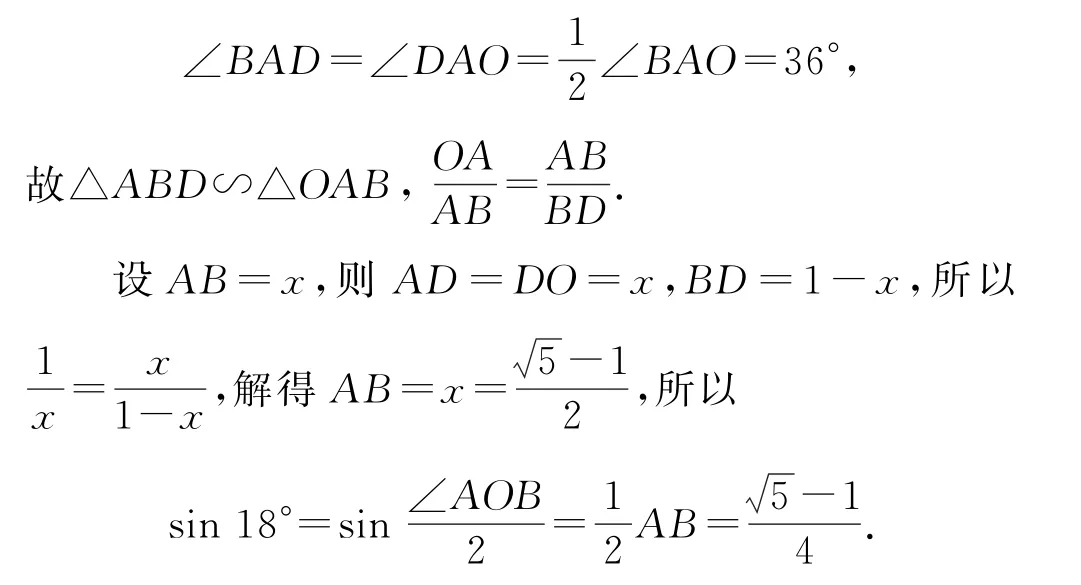
(完)