恒等式和不等式中常量与变量的转化技巧
⦿ 甘肃省武威市第七中学 叶军喜
转化的方法是高中数学解题中最基本的思想方法.数学中很多问题的解决都离不开转化[1].例如,数形结合思想体现了“数”与“形”的相互转化,函数与方程思想体现了函数、方程、不等式之间的相互转化,分类讨论思想体现了局部与整体之间的相互转化,而分析法、反证法、待定系数法、构造法等是转化的具体手段,所以说,转化是数学思想方法的灵魂.
在高中数学中,常量与变量本来是一对矛盾体,很难相互转化,但是,如果站在辩证的角度来看,变量反映的是一个过程,而常量就是变量在某一特定时刻的值.在这种思想指导下,也可以把常量也当作变量来看待,将其放在一个过程中研究,根据解题的需要对常量与变量的位置进行转化,常常能收到意想不到的效果.下面通过对典型例题的解析与点拨,帮助考生熟悉并掌握常量与变量的转化技巧.
1 总体设元法
例1化简:cos2β+cos2(α+β)-2cosαcosβ·cos(α+β).
解析:令x=cos2β+cos2(α+β)-2cosαcosβ·cos(α+β),
y=sin2β+sin2(α+β)-2sinαsinβcos(α+β),
则有
x+y=2-2cos(α+β)cos(α-β),
①
x-y=cos 2β+cos 2(α+β)-2cos2(α+β)=cos 2β+2cos2(α+β)-1-2cos2(α+β)=cos 2β-1.
②
①+②,得2x=2-2cos(α+β)cos(α-β)+cos 2β-1=1-cos 2α-cos 2β+cos 2β=1-cos 2α=2sin2α.
所以x=sin2α.故原式化简为sin2α.
技巧点拨:本题根据题目的特点,采取了总体设元法,构造与其相应的对偶式,运用方程的思想来解决三角恒等变形问题.当然,本题也可以采用降次、和积互化等方法来解决.
2 多元选一法
例2已知|a|<1,|b|<1,|c|<1,求证:
(1)abc+2>a+b+c; (2)ab+bc+ca>-1.
证明:(1)把a看成主元,b,c看成常数,构造关于x的一次函数f(x)=(bc-1)x-b-c+2,则
f(-1)=1-bc-b-c+2=4-(b+1)(c+1),
f(1)=bc-1-b-c+2=(b-1)(c-1).
由|b|<1,|c|<1,可知0 -2 所以0<(b+1)(c+1)<4,0<(b-1)(c-1)<4. 即f(-1)>0,f(1)>0. 所以f(x)在(-1,1)上恒大于0. 因为|a|<1,所以f(a)>0. 故(bc-1)a-b-c+2>0,即abc+2>a+b+c. (2)令g(x)=(b+c)x+bc+1,则 g(1)=b+c+bc+1=(b+1)(c+1), g(-1)=-b-c+bc+1=(b-1)(c-1). 由|b|<1,|c|<1可推知g(-1)>0,g(1)>0. 所以g(x)在(-1,1)上恒有g(x)>0. 又|a|<1,所以g(a)>0. 故(b+c)a+bc+1>0,即ab+bc+ca>-1. 技巧点拨:本题通过灵活变更主元,利用一次函数的单调性来完成证明.由于所证不等式均含三个变量,且三个变量的范围确定,所以采用多元选一法,将其中一个变量看作主元,构造一次函数求解. (1)已知函数f(x)在x=1处取得极值,求a的值; (2)已知不等式f′(x)>x2-x-a+1对任意实数a∈(0,+∞)都成立,求实数x的取值范围. 解析:(1)求导,得f′(x)=ax2-3x+a+1.由函数f(x)在x=1处取得极值,可知f′(1)=0,即a-3+a+1=0,所以a=1. (2)由题设,知ax2-3x+a+1>x2-x-a+1对任意a∈(0,+∞)都成立,即(x2+2)a-x2-2x>0对任意a∈(0,+∞)都成立. 设g(a)=(x2+2)a-x2-2x(a∈R),则对任意x∈R,g(a)为单调递增函数(a∈R),所以对任意a∈(0,+∞),g(a)>0恒成立的充要条件是g(0)≥0,即-x2-2x≥0,解得-2≤x≤0. 所以x的取值范围是[-2,0]. 技巧点拨:本题的第(1)问中,函数f(x)在x=1处取得极值,则f′(1)=0,由此列式即可求出a的值;第(2)问中,已知a∈(0,+∞)时所给不等式恒成立,因此可以将不等式变形,通过构造关于a的一次函数来求解.由此可见,对于涉及两个变量的不等式,如果已给出其中一个变量的范围,则可以构造一个以此变量为主元的函数,然后利用函数的单调性求解. 例4设函数f(x)是定义在(-∞,+∞)上的增函数. (1)如果不等式f(1-ax-x2) (2)如果不等式f(1-ax-x2) 解析:(1)因为f(x)是定义在R上的增函数,所以f(1-ax-x2) 当x=1时,不等式g(a)>0恒成立. 当x>1时,不等式g(a)>0在a∈[0,1]上恒成立. 当x<1时,则只需g(a)=(x-1)a+x2+1在[0,1]上的最小值g(1)>0,即x2+x>0,解得x<-1或x>0,故x<-1或0 综上所述,x<-1或x>0,即x的取值范围为(-∞,-1)∪(0,+∞). 故x∈(-∞,-1)∪(0,+∞). (2)因为f(x)是增函数,所以f(1-ax-x2) 当x=1时,不等式x2+ax+1-a>0对a∈R恒成立. 综上,a∈(-∞,1). 所以函数h(x)的最小值为1. 故a的取值范围为(-∞,1). 技巧点拨:本题的解题思路是利用函数的单调性,把函数值的相对大小问题转化为自变量的大小问题,选取不同的“主元”解决问题.第(1)问采用了“反客为主”法,把a作为变量,x作为常量,降低了计算的难度和繁琐程度,充分体现了变量与常量的对立统一辩证关系;第(2)问采用了“分离常数”法,仍然把x作为变量,把不等式恒成立问题转化为函数的最值问题来解决,巧妙地避开了繁琐的讨论,同样展示了化繁为简的优越性. 从上述对解题思路与方法的点拨中可以看出,常量与变量的转化技巧集中体现在如何“换元”上,实际上是对动态思维、灵活思路的更高要求[2].在解决多变元问题时,要学会逆向思考,换个角度,反客为主,根据需要变更“主元”,拓宽解题思路,达到简捷解题的目的.3 变形构造函数法
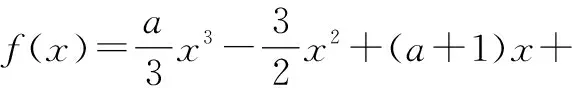
4 反客为主与分离常数法
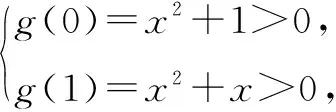
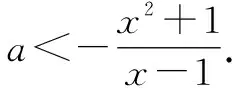
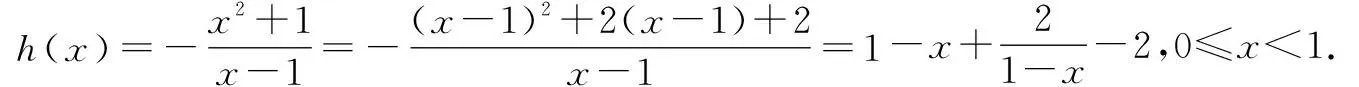
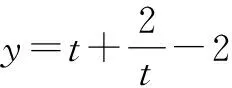
——卡文迪什测定万有引力常量

