圆的性质在圆锥曲线中的推广
胡 丽
(息烽县乌江复旦学校,贵州 贵阳 551100)
在新课程标准下利用向量和圆来研究圆锥曲线的特征与性质,并且在高考中考查圆的性质在圆锥曲线中的推广而得出相应的结论也加强了对能力的考查[1],所以我们在平时教学中对圆性质的应用应该加以重视.
1 垂径定理的推广
圆中有一条性质叫“垂径定理”:若AB为圆O的一条弦,P为AB的中点,则kOP·kAB=-1.

证明设A(x1,y1),B(x2,y2),P(x0,y0),则


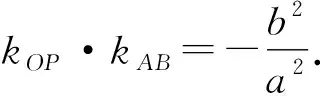

2 圆周角为直角的推广
在圆中有一条必须熟记的就是直径所对的圆周角为90°,即“若AB为圆O的直径,P为圆上异于A,B的任一点,则有kPA·kPB=-1”.这一结论可以在圆锥曲线中进行推广.

证明设A(-x1,-y1),B(x1,y1),P(x0,y0),则




3 切线性质的推广
3.1 圆的性质推广1
AB为圆O非直径的任一弦,圆O在A,B两点的切线交于点P,则OP过弦AB的中点.这一性质在圆锥曲线中可以作如下推广.


图1 圆的性质推广1图

因此,椭圆在点A和点B的切线方程为



所以kOM=kOP.
即O,M,P三点共线.

结论7若过点P作抛物线y2=2px的两条切线PA,PB,过点P作直线PM平行于x轴交弦AB于点M,则点M平分AB(如图2).
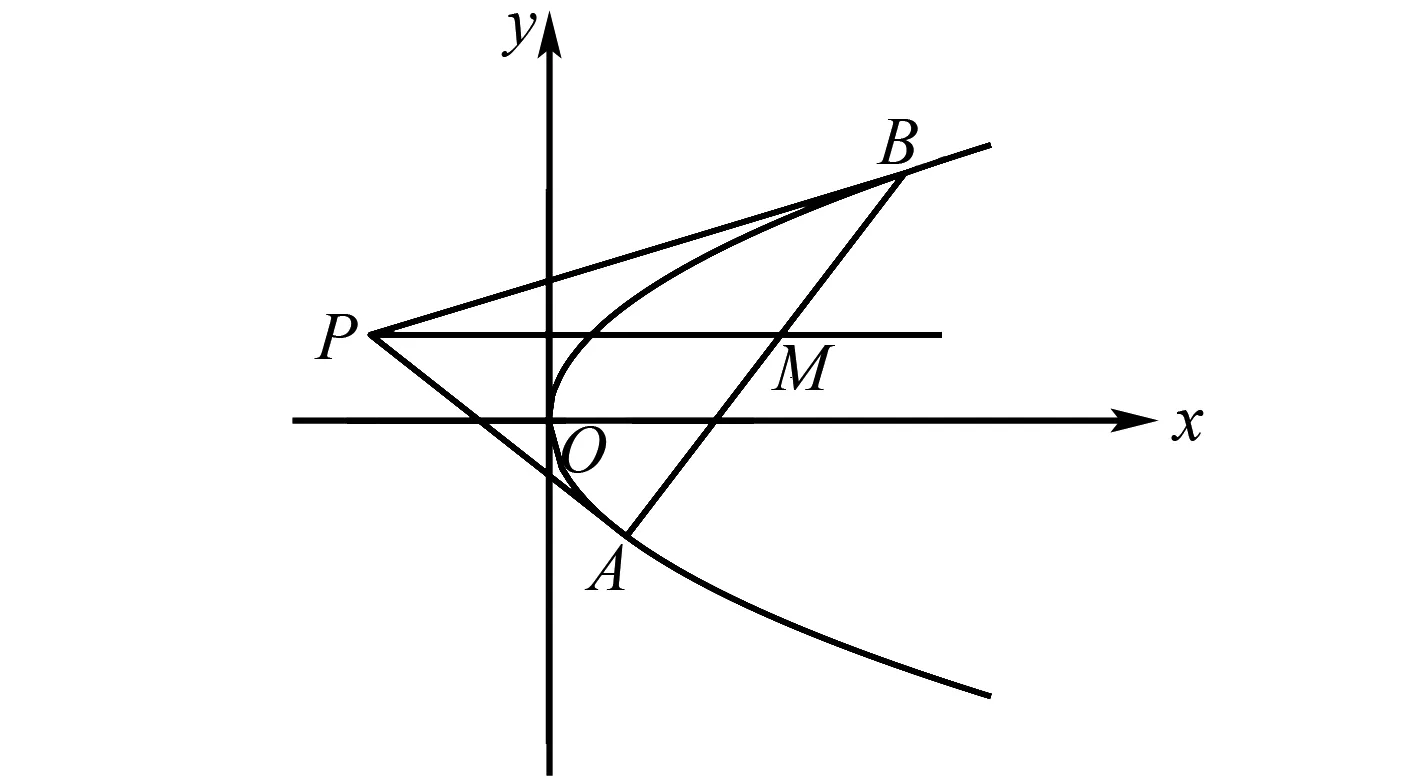
图2 结论7图
3.2 圆的性质推广2
设定点P到圆O上的点A的距离是点P到圆的距离,则圆O在点A处的切线与AP垂直.这一性质推广如下.
结论8 设定点P(a,b)到圆锥曲线C上的点A的距离是点P到曲线C距离,则曲线C在点A处的切线与AP垂直.
证明设A(x0,y0),圆锥曲线在点P附近的单调曲线段为一个函数y=f(x),则
令y=(x-a)2+[f(x)-b]2,则
y′=2(x-a)+2[f(x)-b]·f′(x).
由于定点P(a,b)到圆锥曲线C上的点A的距离是点P到曲线C距离,所以y′|x=x0=0.


4 两垂直割线的推广
我们知道圆内接直角三角形的斜边恒过一定点(圆心),通过特例的检验、大胆猜想、合理的证明,我们可以将这一性质推广到圆锥曲线上.
结论9 设P(x0,y0)是抛物线y2=2px上一定点,A,B是抛物线上两点,且满足PA⊥PB,则AB过点(2p+x0,-y0).
证明设A(x1,y1),B(x2,y2)是抛物线上两点,由PA⊥PB,得
(x0-x1)(x0-x2)+(y0-y1)(y0-y2)=0.
化简可得(y0+y1)(y0+y2)=-4p.
所以y1y2=-4p-(y1+y2)y0-2px0.
另一方面,当x1≠x2时,
故AB所在直线方程为

所以直线AB恒过定点(2p+x0,-y0)(经检验当x1=x2时也成立).


通过对圆的重要性质的推广,我们不难发现,圆的一些重要性质在解决圆锥曲线的问题时,使某些比较复杂难解的问题简单化、明朗化,使学生对书本上的知识更容易理解,开拓了学生的数学眼界[2].
在高中数学教学中引导学生去探究这些统一性质,学生在解圆锥曲线题的过程中可以得心应手,也能培养学生对数学的探究热情,更使学生在探究数学的过程中提升自己的数学素养.

