对一道高中数学联赛解三角形问题的探析
2023-10-11 01:09:48刘海涛
数理化解题研究 2023年25期
刘海涛
(安徽省芜湖市第一中学,安徽 芜湖 241000)

分析该题结构虽简单、明了,但内涵丰富、解法灵活,主要考查了正弦和余弦定理、三角恒等变换、三角形面积公式、构造图形表示几何关系等知识,强化了学生分析问题、解决问题的能力及转化与化归、数形结合的数学思想,体现了逻辑推理、数学运算、直观想象等数学核心素养.文章从不同角度探析该题,给出了九种不同解法,现与读者分享交流.
1 解法探究









由sinA=sin(B+C)=sinBcosC+cosBsinC,
及sin(B-C)=sinBcosC-cosBsinC,得


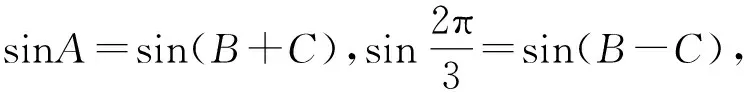








如图1,过点B作BD⊥AC于点D,则

图1 作高示意图
BD=AB·sinA=BC·sinC,
AC=BC·cosC+AB·cosA.
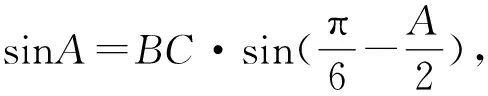
联立两式整理,得

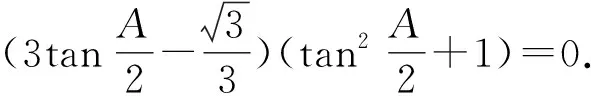

评注注意到该题的目标为sinA,接下来考虑构造关于角A的三角恒等式,变换化简即可解题.



图2 构角相等示意图

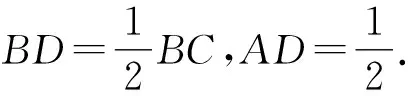
在△BCD中,
CD2=BD2+BC2-2BD·BC·cos∠CBD,

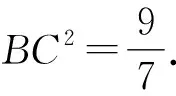






图3 构两边相等图
在△ABD中,
AD2=AB2+BD2-2AB·AD·cos∠ABD,
即(2-BD)2= 1+BD2+BD.





解法7如图4,延长CB至点D,连接AD,使得AD=AC.
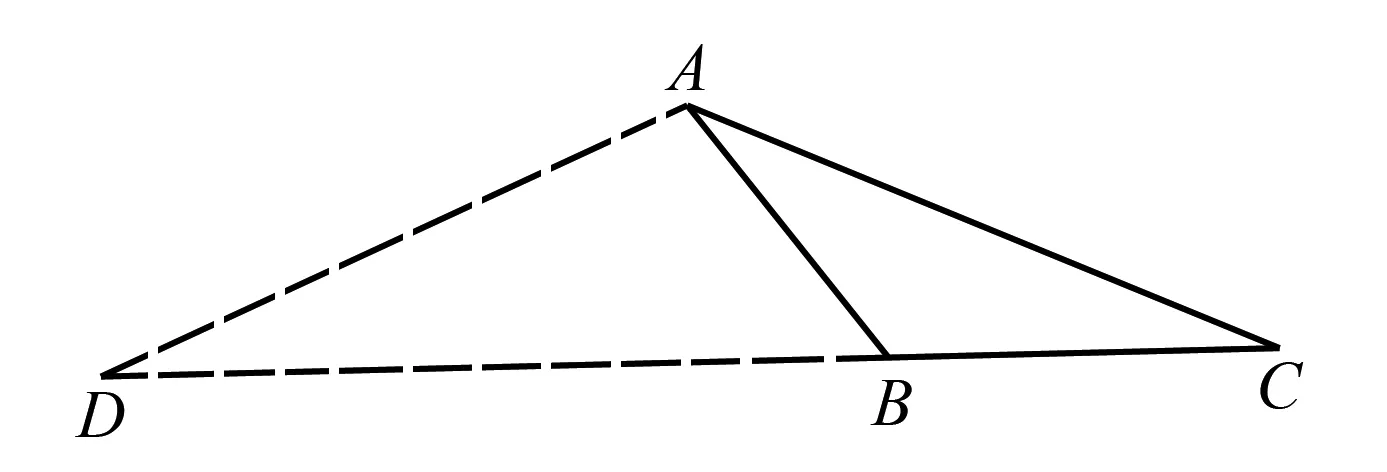
图4 构两边相等图


由∠ABD+∠ABC=π,得
cos∠ABD+cos∠ABC=0.
由余弦定理,得
代入数值计算,得


解法8如图5,延长AB至点D,连接CD,使得∠ACB=∠DCB.

图5 构两角相等图

在△ADC中,
AC2=CD2+AD2-2CD·AD·cos∠ADC,
即4=4BD2+(1+BD)2+2BD(1+BD).






图6 构等腰梯形图

易知等腰梯形存在外接圆,故由托勒密定理,得
AD·BC+AB·CD=AC·BD.


2 反思总结

猜你喜欢
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
河北理科教学研究(2020年4期)2020-03-09 03:34:52
中学数学教学(2019年3期)2019-06-21 08:10:52
中等数学(2018年8期)2018-11-10 05:07:22
中学数学杂志(高中版)(2018年1期)2018-01-27 18:49:49
智富时代(2017年4期)2017-04-27 02:13:48
中学教学参考·理科版(2014年3期)2014-04-10 09:12:52
今日中学生(初三版)(2013年6期)2013-07-30 06:29:40

