基于蒙特卡罗方法的飞行过载超越数模拟技术

郭俊辰,冯建民,2

(1.中国飞机强度研究所,陕西 西安 710065;2.全尺寸飞机航空科技重点实验室,陕西 西安 710065)

1 引 言

现有飞机疲劳试验载荷谱编制主要建立在过载超越数曲线的基础上。为获得飞机的过载超越数曲线,需进行大量飞机服役载荷统计及飞行载荷实测工作。国内航空工业起步相对较晚,载荷数据的积累依然较少,难以合理预估新机的过载超越数曲线,影响了载荷谱的编制和飞机疲劳寿命的评估。

国内外学者对过载超越数曲线进行了大量研究和分析,发现了其具有的一些统计特征。Reyer针对通用小飞机的过载超越数进行了研究,认为在指定过载下,超越数可以用对数正态分布来描述[1]。王长江等对多型号商用运输机的研究也表明,可采用对数正态分布来描述过载超越数曲线族[2]。Aalt总结了民用飞机和军用飞机过载超越数曲线的大致趋势,二者由于飞行任务不同,表现为军用战斗机的载荷谱呈外凸形、民用运输机的载荷谱呈内凹形的特点[3]。

在飞行载荷的模拟研究中,Monte Carlo方法被广泛采用。早期,Ocampo等针对小型通用飞机,使用Monte Carlo方法进行了数值模拟试验[4],将超越数、飞行距离和速度、下沉速度均设定为随机变量,这提供了一种过载超越数曲线族的模拟思路[5]。王长江针对商用客机的过载数据进行了研究,提出分别对飞行距离、突风速度超越数、机动过载超越数进行随机抽样得到总载荷谱的方法[6]。朱俊贤等同样利用Monte Carlo方法,模拟得到机群中不同单机的阵风速度超越数时间历程,该方法采用单一的随机变量的抽样得到超越数结果[7]。

本文在研究飞机的过载超越数曲线统计特征的基础上,确定建立超越数曲线模型的核心参数,形成过载超越数曲线的模拟方法。通过对多个变量的随机抽样,得到随机过载数据,最后验证利用模拟数据得到的机群过载超越数中参数是否符合预期设定。验证后的模型和方法可为载荷谱编制提供足够的、可信的过载数据,为载荷谱编制方法研究和评估提供依据。过载超越数模拟技术路线如图1所示。

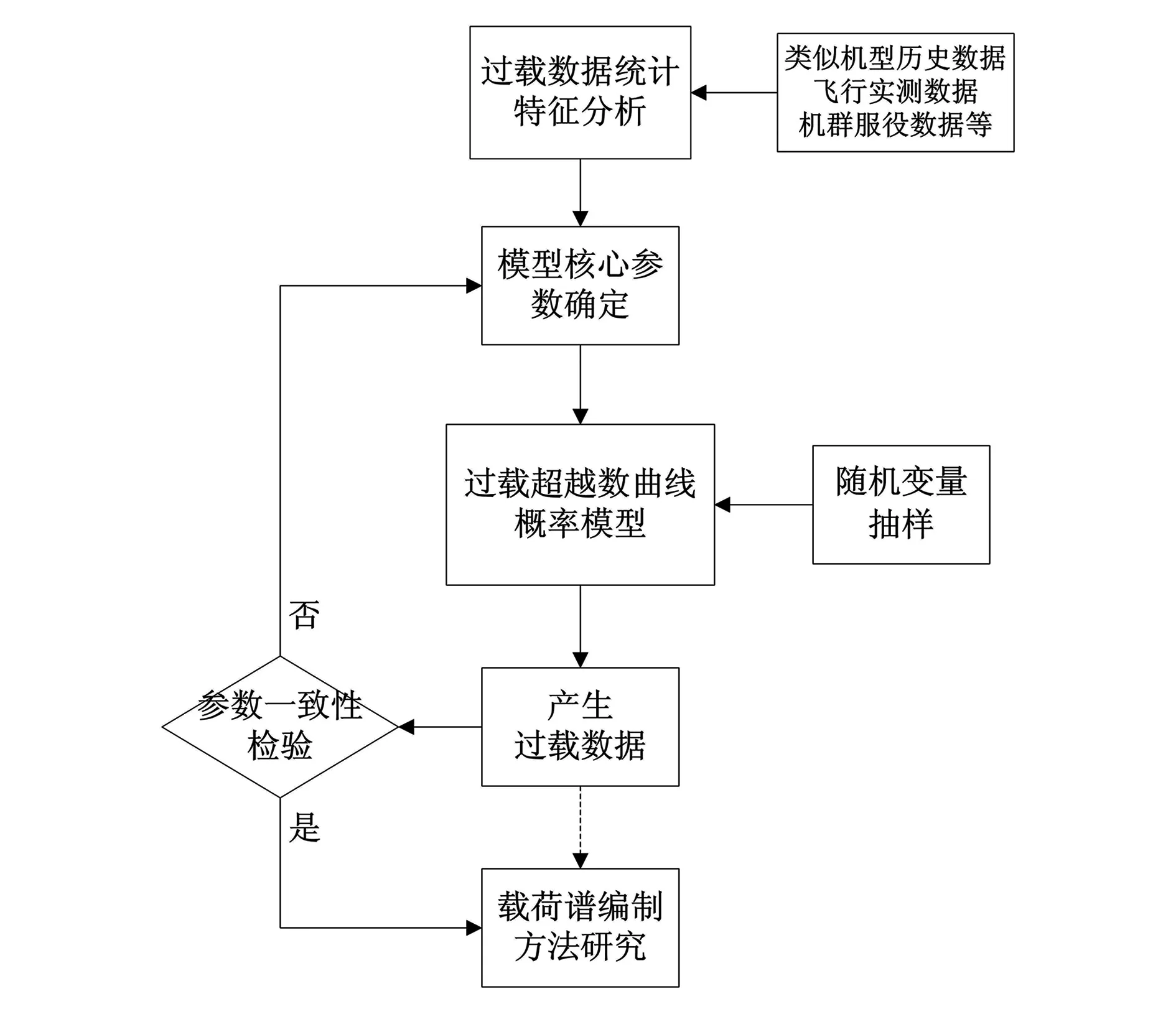
图1 过载超越数模拟技术路线

2 飞行过载统计特征分析

飞机在飞行过程中会受到一系列载荷的作用,体现在飞机重心过载时间历程上就是过载波形曲线。应用各种过载统计计数方法可以得到过载频数表格、过载超越数曲线等,以直观的形式展现其特征。

对部分国外军、民机型进行统计[8-12],其过载超越数曲线如图2、图3所示。对过载超越数曲线族的曲线趋势、分散性等进行分析,对其统计特征进行归纳。

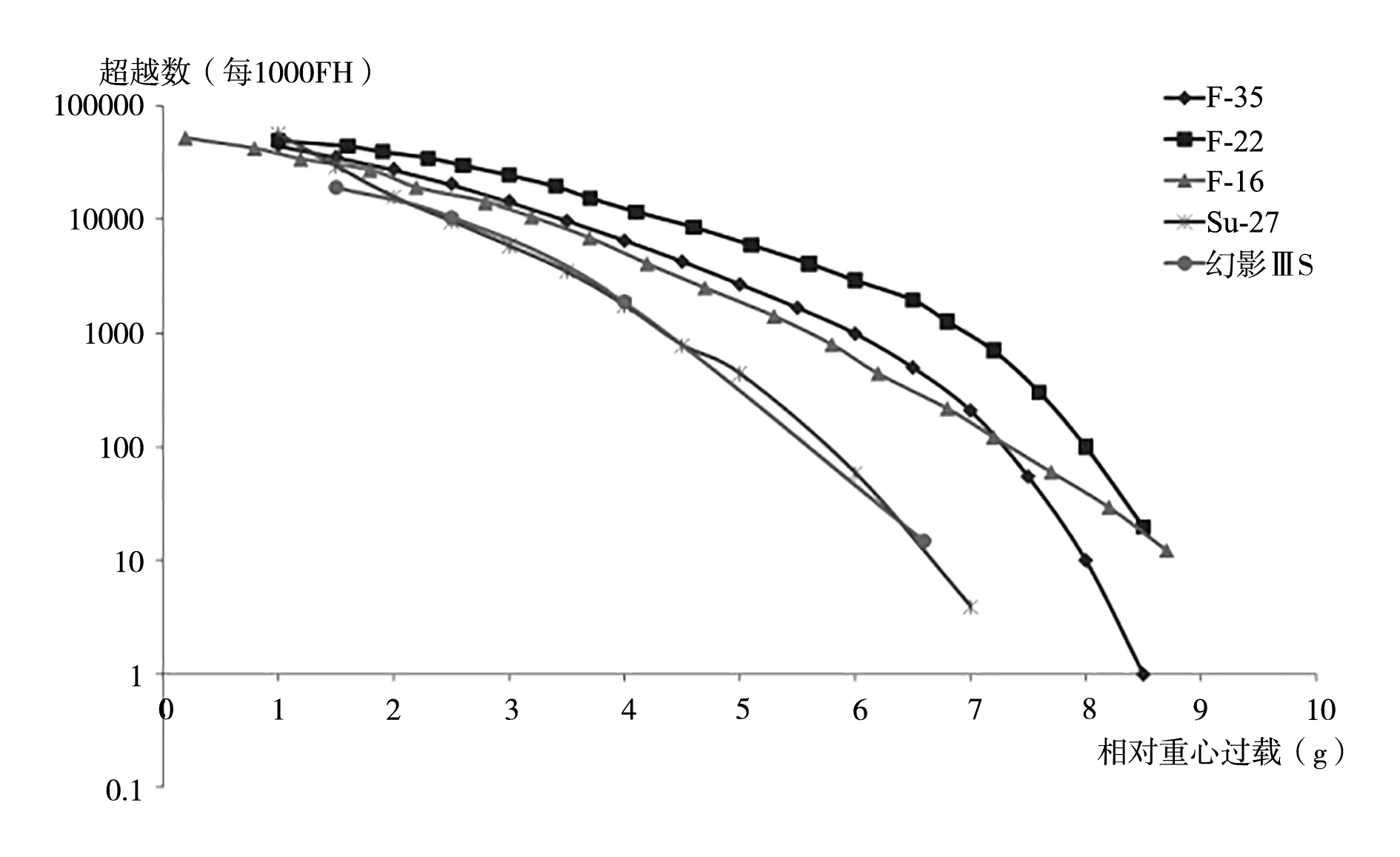
图2 部分军机过载超越数曲线

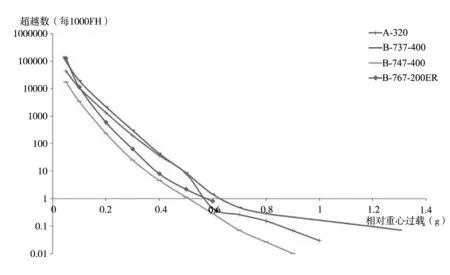
图3 部分民机过载超越数曲线

2.1 均值曲线拟合

过载超越数曲线族的均值曲线能够拟合为一条曲线,在一般情况下,可用对数多项式方程来进行曲线拟合[13]。为了简化模型,本文不考虑曲线变化剧烈的两端数据。以战斗类飞机为例,将忽略过载小于1g和超越数小于10次的数据。建立过载超越数拟合曲线为:

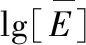
2.2 指定过载超越数分布

相关文献的研究结果表明[1,2],机群过载超越数曲线族中,指定过载下的超越数服从对数正态分布。本文采用该假设建立模型,即在指定一过载nz下,超越数满足:

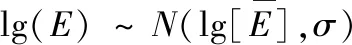
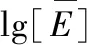
2.3 超越数曲线的概率密度

飞机飞行过载实测数据以过载超越数曲线F(nz)的形式给出,该曲线代表过载发生的累积频数趋势。因此,对过载超越数曲线求导所得f(nz)=F′(nz)代表过载发生频数曲线。借用概率统计中分布函数与概率密度函数的定义,将f(nz)称为过载发生的概率密度函数。

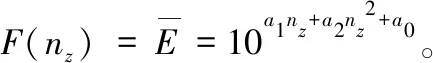
2.4 曲线形状参数

利用点到直线的距离计算公式,得到过载超越数曲线与端点连接直线切点到直线的距离,定义该距离为过载超越数曲线的形状参数,用α表示。计算结果为:

该形状参数反映了过载超越数曲线的凹凸性质。在新机型研制过程中,可以通过类比以往相似机型的过载超越数曲线,合理选取该形状参数。因此,确定好曲线端点值及形状参数后,结合2.1节参数性质的判断,可以计算得到过载超越数曲线的各项参数值a0、a1、a2。

利用2.3节中的标准化转换方法,将过载超越数曲线端点值标准化为(0,1)、(1,0)后,可以将斜率、截距公式合理简化为k=-1、b=1,由此得到更为简单的表达式。

2.5 服从分布的随机数获得

运用Monte Carlo中取舍算法的思想,在不能简单地通过某一个已知分布直接得到抽样结果时,可以在一个构造好的分布下生成一堆随机数,然后在这些样本中按照一定的方法取舍,得到最终结果,以此建立随机过载生成流程。

首先建立两个随机数un、ub,其中,un代表过载值的随机数,ub为辅助随机数,用于确定随机数un的分布特性。数据对(un,ub)可以视为从一个矩形平面区间中均匀取得的一个点,两随机数代表该点坐标,概率密度函数曲线在该平面中为一曲线,其与x轴包围区域即为所需数据,其他数据将作剔除处理。该思路可以用图4展示,其中点(un1,ub1)予以保留,点(un2,ub2)予以剔除。

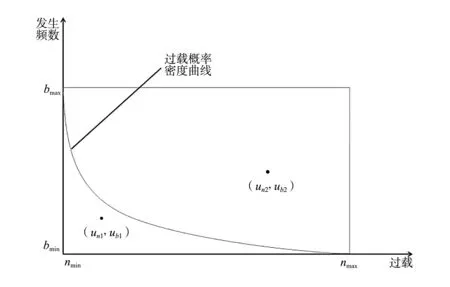
图4 过载随机数生成

将上述过程用公式表示为:

un～MC{[nmin,nmax],[bmin,bmax],H(un)}

其中,[nmin,nmax]为过载随机数边界,[bmin,bmax]为辅助随机数边界,H(un)为由概率密度函数得出的判定函数。

综上,图5所绘为依据前文归纳总结得到的机群过载超越数曲线族统计特征示意图。

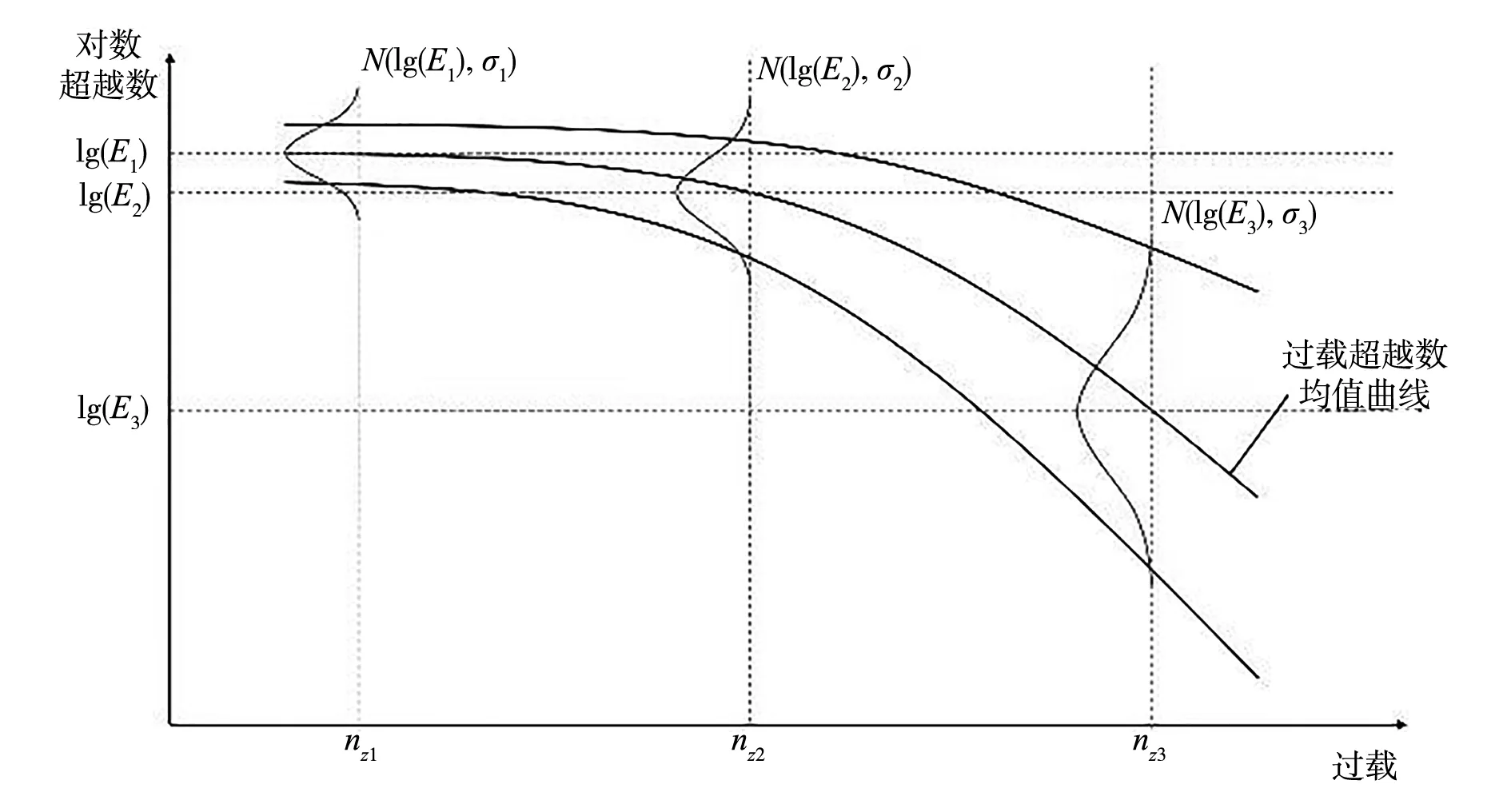
图5 机群过载超越数曲线族统计特征

3 过载超越数模拟模型建立

本模型单机飞行过载模拟数据生成从两方面进行:一是确定单机含有相对重心过载峰谷对数量,即单机飞行含有多少峰值(谷值)过载,本文称之为总过载发生频数,用Nt表示;二是得到服从预定分布的随机飞行过载数据,其数量等于总过载发生频数,该过载数据为随机量,用un表示。然后多次进行模拟以得到机群的过载数据,并统计得到机群过载超越数。

3.1 过载模拟模型

将过载模拟过程利用公式进行描述:式(1)为过载超越数均值拟合曲线形式;式(2)为指定过载下,超越数随机值生成方法;式(3)为利用Monte Carlo方法得到随机过载的过程表达式。

(1)

(2)

(3)

其中,过载超越数均值拟合曲线系数a0、a1、a2及过载边界处对数超越数分布标准差σmin、σmax均为本文模型中初始输入参数,由类似机型的载荷数据类比并计算得到。

3.2 模型实现流程

以峰值过载为例,飞机飞行过载随机数生成步骤如下:

(1)由类似机型过载数据类比得到曲线端点值(nz1,lg(E)1)、(nzn,lg(E)n),曲线形状参数α以及超越数分散性参数σmin、σmax。通过计算,得到均值过载超越数拟合曲线各项系数a0、a1、a2。

(2)生成服从均匀分布的随机数un、ub,用公式分别表示为un～U(nmin,nmax)、ub～U(bmin,bmax)。

(3)将2.3节中概率密度函数公式作为判定函数、过载的随机数un为函数自变量,即:

当0

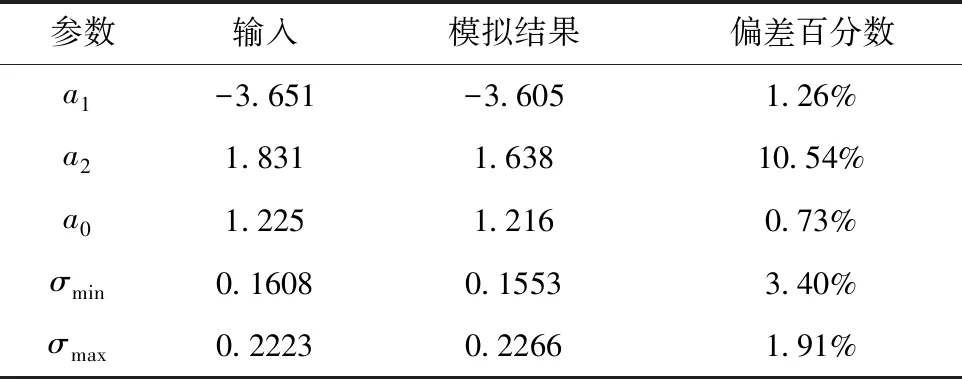
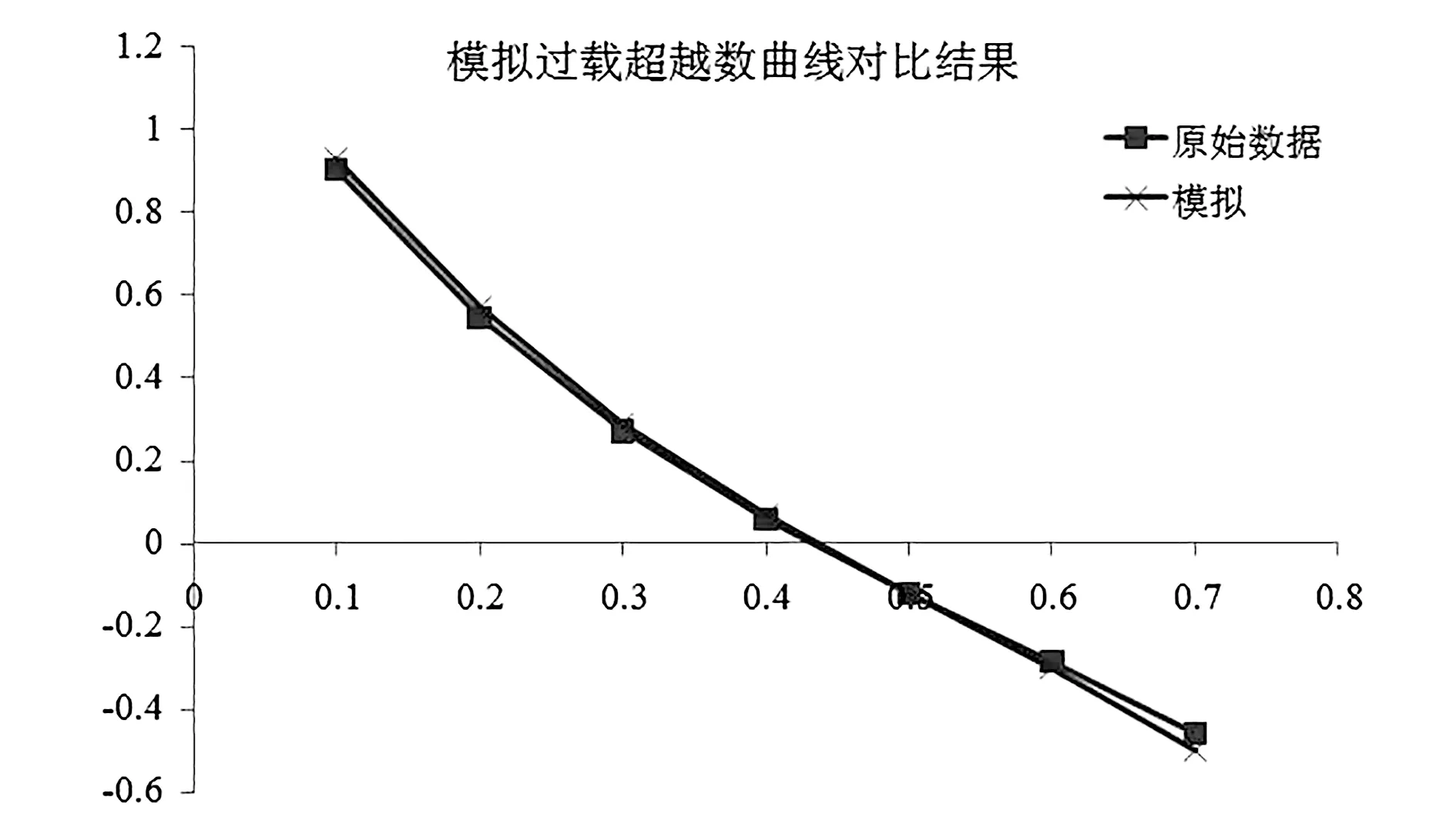
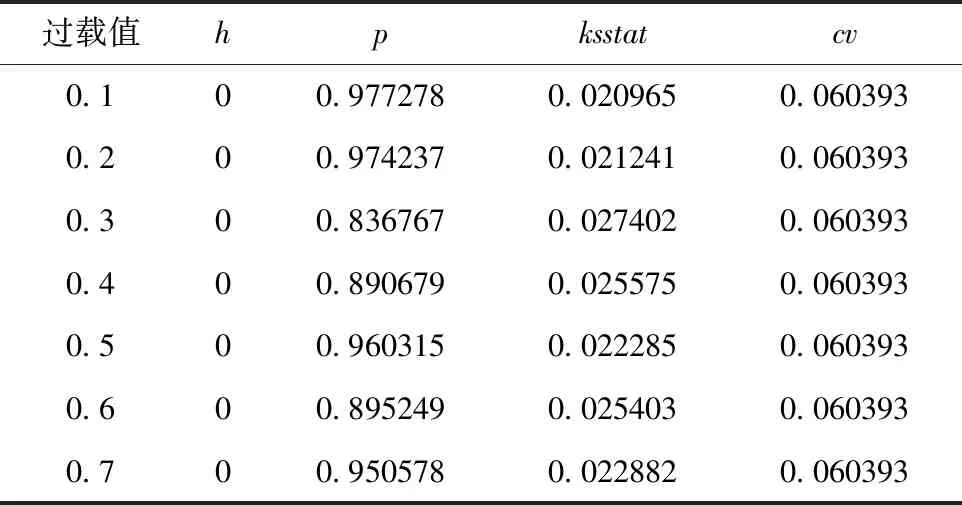
3.3 随机过载应用

飞机飞行历程所受过载的模拟需要确定其过载发生频数,可以通过两个方法来对其进行确定:一是结合飞行任务指南,确定在某飞行历程下过载发生频数值;二是通过某飞行历程下的过载超越数曲线,结合曲线族分散性,引入随机变量,计算得到过载发生频数。

若指定飞行历程为单机全寿命历程,重复多次得到多个单机的全寿命历程过载,即为机群过载超越数数据。将过载区间(nmin,nmax)分为多个子区间,逐步累加计算得到过载超越数,可以绘制出过载超越数曲线。

4 模型评估

4.1 参数选取

本文参考P-2V飞行巡航段过载实测数据[14],类比该数据曲线形状,设定模型过载超越数曲线形状参数为α=0.5194。同样地,确定过载超越数曲线两端点值分别为(0.1,0.9012)及(0.7,-0.4568)。

依据2.4节所述,得到拟合曲线各项系数。同样地,依据类似机型的分散性数据,设定标准差参数输入值。模型采用的均值拟合曲线表达式系数及超越数分散性相关参数如表1所示。

表1 模拟过载超越数参数对比

4.2 模拟结果分析

运用模型进行模拟计算,设定机群单机数量为500,得到模拟过载结果。将得到的机群过载超越数取对数均值,绘制得到机群飞行均值过载超越数曲线,将该结果与原始数据对比,如图6所示。可以看到,利用模拟过载所得曲线与原始数据重合度高,模拟结果的均值与原始数据均值相吻合。

图6 均值过载超越数结果对比

计算模拟的机群过载超越数各项参数,得到表1所示结果,可以看到,各参数符合度高,基本可以认为本模型得到的模拟结果达到了预期效果,可以比较真实地反映实际过载发生情况。

为了验证所得模拟数据的分布特性,对每级过载下对数超越数进行单样本K-S检验,如表2所示。可以看到,每级过载下对数超越数正态拟合度好,认为每级过载下对数超越数服从正态分布的假设。

表2 各过载下超越数K-S检验结果

综上所述,将本模型得到的模拟结果与原始的实测数据进行对比,可以证明,利用模型得到的随机过载绘制的机群过载超越数曲线族均值与原始数据符合较好,且曲线族在每级过载下分布服从对数正态分布,符合预期想要得到的分布特征。本模型能够得到合理的飞机机群飞行过载数据,该模拟数据与飞行实测数据拟合较好,且能够反映机群过载分散性。

5 结束语

依据机群过载超越数曲线族的统计特征,本文成功建立了一种飞机机群过载超越数曲线族模拟方法。该方法从过载超越数曲线得到飞行过载概率密度函数,基于各过载下超越数服从对数正态分布,构建了反映超越数均值和分散性变化趋势的模型,最终得到机群的总过载超数曲线。通过初步分析,该模拟方法得到的数据符合要求,能够很好地反映机群过载超越数的总体统计特征。

后续飞机机群过载超越数曲线的模拟研究还可以有以下的突破方向:(1)结合飞机飞行任务段和任务剖面的划分,探讨综合不同任务段的各种不同任务剖面下,飞机过载模拟的效果;(2)利用该模拟方法得到的数据来进行疲劳载荷谱编制方面的研究工作,探讨该思路的可行性;(3)结合飞机结构分散性进行飞机疲劳寿命方面的研究,综合考虑载荷谱和结构二者的分散性对飞机机群损伤的影响。