夹芯梁在重物低速冲击下的动力计算分析
肖 珍,吴 晓
(1.常德学院 智能建筑学院,湖南 常德 415000;2.湖南文理学院 机械工程学院,湖南 常德 415000)
1 引 言
有关研究夹芯结构受冲击的文献较多。文献[1]研究了泡沫填充的S形褶皱复合材料夹芯板低速冲击响应特性,文献[2]研究了冲击载荷下轻质夹芯拱最大刚度拓补优化及动力响应,文献[3]研究了嵌锁式CFRP方形蜂窝夹芯梁低速冲击响应及失效机理,文献[4]研究了起圈织物泡沫夹芯复合材料低速冲击性能,文献[5]研究了泡沫金属夹芯梁在重复冲击下的动态响应,文献[6]研究了船用蜂窝金属夹芯板重复冲击实验,文献[7]研究了S形碳纤维褶皱夹芯结构低速冲击响应特性实验,文献[8]研究了横向冲击载荷下不同约束泡沫铝夹芯圆管的动态响应,文献[9]研究了横向冲击载荷下泡沫铝夹芯双圆管的吸能,文献[10]研究了低速冲击下金属蜂窝夹芯板抗侵彻性能的试验。
以上文献研究夹芯结构受冲击时的动力特性,多采用数值计算法或试验法,没有给出直接有效的解析计算法。基于上述因素,本文采用能量原理研究了夹芯梁在重物低速冲击下的动力计算。
2 夹芯梁的能量方程
假设图1所示的夹芯梁截面上、下面板厚度很薄,不承担剪力,梁截面剪力全部由夹芯层来承担。
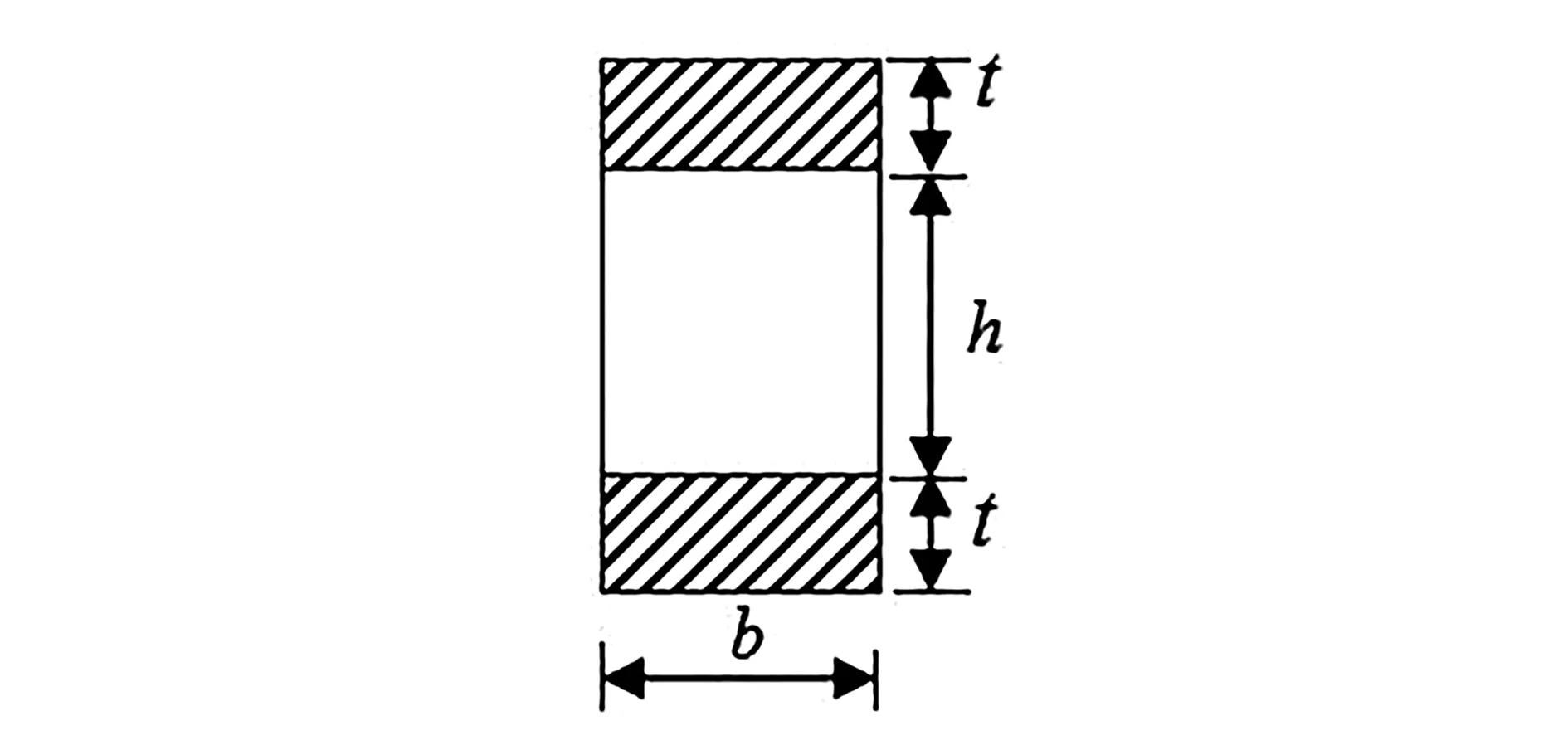
图1 夹芯梁截面
由材料力学可得图1所示夹芯梁截面正应力为:
(1)

取图2所示夹芯梁微段来推导梁截面的剪应力公式。

图2 夹芯梁微段
图2所示夹芯梁微段左边轴向力为:

(2)
同理,图2所示夹芯梁微段右边轴向力为:

(3)
而图2所示夹芯梁微段平衡方程为:
N1+τbdx=N2
(4)
把式(2)、式(3)代入式(4),可得夹芯梁截面剪应力公式为:
(5)
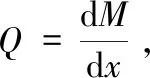
由弹性理论可得夹芯梁的单位体积能量为:
(6)
式中,G2为夹芯层的剪切弹性模量。
由式(6)可得夹芯梁弯曲应变能为:
(7)
式中,V为夹芯梁微段体积。
把式(1)、式(5)、式(6)代入式(7),可得夹芯梁弯曲应变能表达式为:
(8)

若求作用力P下的挠度,利用式(8)可得:
(9)
为了检验本文方法的计算精度,可把本方法计算结果与文献[11]的试验结果进行比较。文献[11]试验用夹芯梁材料参数为:上、下面板厚度均为t=2.4mm,b=80mm,h=38mm,E1=8.73GPa,E2=1.469GPa,G2=0.209GPa。
试验1。文献[11]利用三点弯曲试验研究了图3所示夹芯梁的力学特性。

图3 三点弯曲夹芯梁
利用式(9)可以求得梁中点挠度为:
(10)
用式(10)得到的计算结果与文献[11]的试验结果如表1所示。

表1 三点弯曲夹芯梁中点挠度
试验2。文献[11]利用四点弯曲试验研究了图4所示四点弯曲夹芯梁的力学特性。

图4 四点弯曲夹芯梁
利用式(9)可以求得梁中点挠度为:
(11)
用式(11)得到的计算结果与文献[11]的试验结果如表2所示。
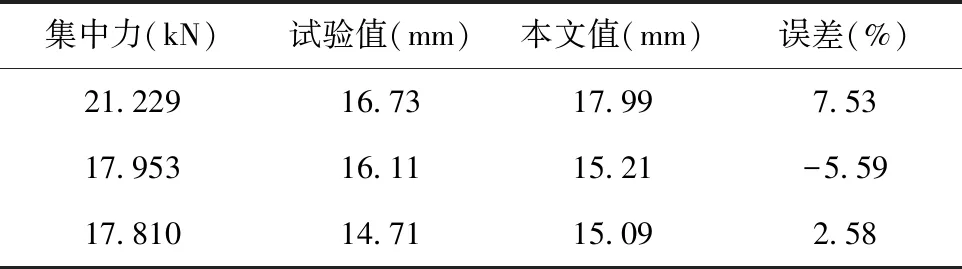
表2 四点弯曲夹芯梁中点挠度(l=450mm,a=150mm)
利用式(1)计算文献[11]抗弯刚度D=1.907GN·mm2,与文献[11]试验结果1.937GN·mm2的误差为-1.55%。
对表1、表2进行分析可以看出,本文方法的计算结果与文献[11]的试验结果基本吻合,仅表1中夹芯梁长l=450mm时本文方法计算结果与文献[11]试验结果的误差为16.24%,导致误差较大的原因可能有:一是夹芯梁在制作上存在工艺误差,二是夹芯梁的支承状况不理想,三是夹芯梁加载时在梁中点可能产生偏心矩。
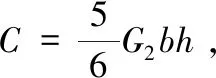
3 重物对夹芯梁的冲击
以图5所示重物对夹芯梁的冲击为例,讨论分析夹芯梁在重物低速冲击下的动力计算。

图5 重物对夹芯梁的冲击
为简化计算可作以下假设:(1)冲击过程中不存在能量损失;(2)冲击过程中不考虑夹芯梁的阻尼;(3)冲击过程中梁的变形皆在弹性范围内;(4)梁受冲击点不发生塑性变形。
图5所示重物对夹芯梁冲击时,与梁接触前瞬间其速度为:
(12)
所以,重物与梁冲击时接触前瞬间的动量为M0v0。而重物与梁接触后瞬间,梁在冲击点获得速度v,而梁除冲击点以外部分的速度皆不相同且不等于v。因此,可假设夹芯梁质量m折减为em(e<1)集中于冲击点处,这样重物与梁冲击接触后瞬间应满足动量守恒原理:
M0v0=(M0+em)v
(13)
式中,e为折减系数。
由式(13)可以求得:
(14)
根据前面所作假设,重物对梁冲击时的势能与动能之和应等于梁变形后的应变能,即:
(15)
式中,Δd为梁受冲击后的动变形。
以图5所示的重物对夹芯梁冲击为例,利用式(8)可得梁的应变能为:
(16)
式中,Pd为梁受冲击时的动载荷。
梁受冲击后的动变形为:
(17)
利用式(14)-式(17)可以求得动变形为:
(18)
所以,重物冲击夹芯梁时的动载荷系数为:
(19)
为了确定折减系数,可令梁的动能与梁折减到冲击点处的动能相等,即:
(20)
式中,ρ为梁的密度,A为梁的横截面面积,m为梁的质量,w(x,t)为梁的动位移。
以图5所示夹芯梁为例,假设动位移函数为:
(21)
式中,T(t)为时间函数。
把式(21)代入式(20)中可以求得:
(22)
下面讨论剪切刚度、折减系数等因素对夹芯梁受冲击时的影响。夹芯梁参数为:l=3m,b=200mm,h=300mm,t=12mm,E1=210GPa,E2=10GPa,G1=79.38GPa,G2=0.5GPa,[σ1]=170MPa,[σ2]=10MPa。
首先确定夹芯梁许用载荷,即图5所示夹芯梁在弹性范围内可以承受的最大冲击载荷。
由式(1)可得:
(23a)
(23b)
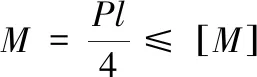
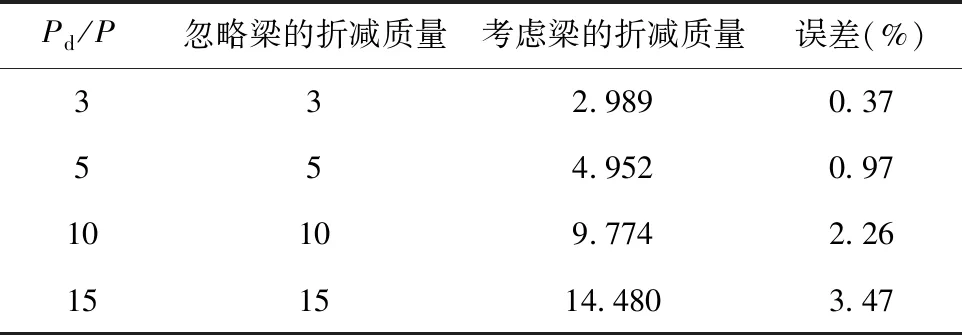
表3 动载荷系数Kd
在表3中,以Pd=193.4933kN为极限,重物在相同的高度对夹芯梁冲击,即使Pd/P=15时,考虑夹芯梁折减质量的动载荷系数与忽略夹芯梁折减质量的动载荷系数误差也仅为3.47%,这主要是夹芯梁的质量仅为m=209.52kg,与冲击重物的质量相比太小。因此,如果梁的质量与重物质量相比很小时,折减系数e对动载荷系数的影响可以忽略不计。
由式(17)可知,忽略剪切刚度时动变形与考虑剪切刚度时动变形的误差为:
(24)
把图5所示的夹芯梁有关参数代入式(24)中,可知忽略剪切刚度时梁的动挠度与考虑剪切刚度时梁的动挠度误差为δ=5.49%。从本文的计算结果来看,剪切刚度对夹芯梁的动力计算有较大的影响。
4 结 论
(1)利用能量法推导了夹心梁截面剪应力、抗弯刚度、剪切刚度和集中力作用下的挠度计算表达式,与文献[11]的试验值进行比较,可知本文提出的计算方法具有较高的精度。
(2)夹芯梁面板弯曲正应力对夹芯层的剪切变形是有较大“贡献”的。计算夹芯梁弯曲挠度时,要考虑面板弯曲应力对夹芯层剪切刚度的影响,否则会导致理论计算结果与试验结果存在较大的误差。
(3)梁的质量与重物质量相比很小时,折减系数e对动载荷系数的影响可忽略不计。
(4)忽略剪切刚度时夹芯梁的动挠度与考虑剪切刚度时夹芯梁的动挠度存在较大的误差。从本文计算结果来看,剪切刚度对夹芯梁的动力计算有较大的影响。

