基于系统辨识建模的控制器分析
王文丽,周 挺
(中国飞机强度研究所,陕西 西安 710065)
1 引 言
电液力反馈控制系统具有传递功率大、响应快、控制精度高等特点,广泛应用于飞机结构静强度试验。系统工作原理为控制器根据上位机的给定值和测力传感器的反馈值之差控制电液伺服阀阀口开度,从而调节液压缸两腔油液体积比,将载荷施加至试件,完成力控模式的闭环控制。MOOG控制器是飞机结构静强度试验的常用控制器,其特有的PIDF(比例-积分-阻尼-前馈)控制器为系统提供了较好的稳定裕度,在外界参量变化的情况下,相同的控制参数仍能实现满意的稳态和瞬态性能指标。
电液力反馈控制系统受现场环境波动引起的参量变化和各环节耦合影响,采用机理法难以建立系统的精确数学模型[1,2]。采用系统模型辨识的方法,通过MATLAB系统辨识工具箱(System Identification Toolbox)建立了电液力反馈控制系统的数学模型,并基于辨识的模型仿真分析了MOOG控制器中阻尼环节和前馈环节的控制特性。
2 系统辨识过程
借助系统辨识工具箱[3],选择线性参数模型Polynomial Models的ARX:[nanbnk]和ARMAX:[nanbncnk]分别对系统ARX模型和ARMAX模型进行参数模型辨识,对两种模型进行拟合度对比、残差分析和阶次对比,得到系统最终的辨识模型[4]。
2.1 辨识数据的获取
搭建单通道电液力反馈控制系统试验平台,选用液压缸硬式连接自平衡框架的加载形式,测力传感器选用20kN,液压缸选用30kN。图1为MOOG控制器原理图,设置比例增益kp=1,积分增益ki=0,阻尼增益kd=0,前馈增益kf=0,使控制器为单位增益。对系统施加周期为3.33s的等幅正弦输入信号,范围为+4kN~+12kN,采样时间为0.01s。获取8个加载周期的试验数据,将输入输出数据归化为满量程的百分比值,并依次按列保存至data.xls的excel文件中,共2664组数据,导入MATLAB工作空间。原始输入输出数据如图2所示,u1为输入变量,y1为输出变量。

图1 MOOG控制器原理图

图2 原始输入输出数据
2.2 数据预处理
试验中所测数据常包含有线性项或缓慢变化的趋势项,其对辨识精度的影响无论采用何种辨识方法都难以消除。因此,辨识前须对测量数据进行预处理。
利用MATLAB系统辨识工具箱的预处理函数(detrend)对数据进行处理,把数据的趋势项消除,即得到测量数据均值为0的平稳过程,如图3所示。将预处理后的数据分为2部分:前4个周期的数据作为工作数据进行模型辨识,后4个周期的数据作为验证数据。
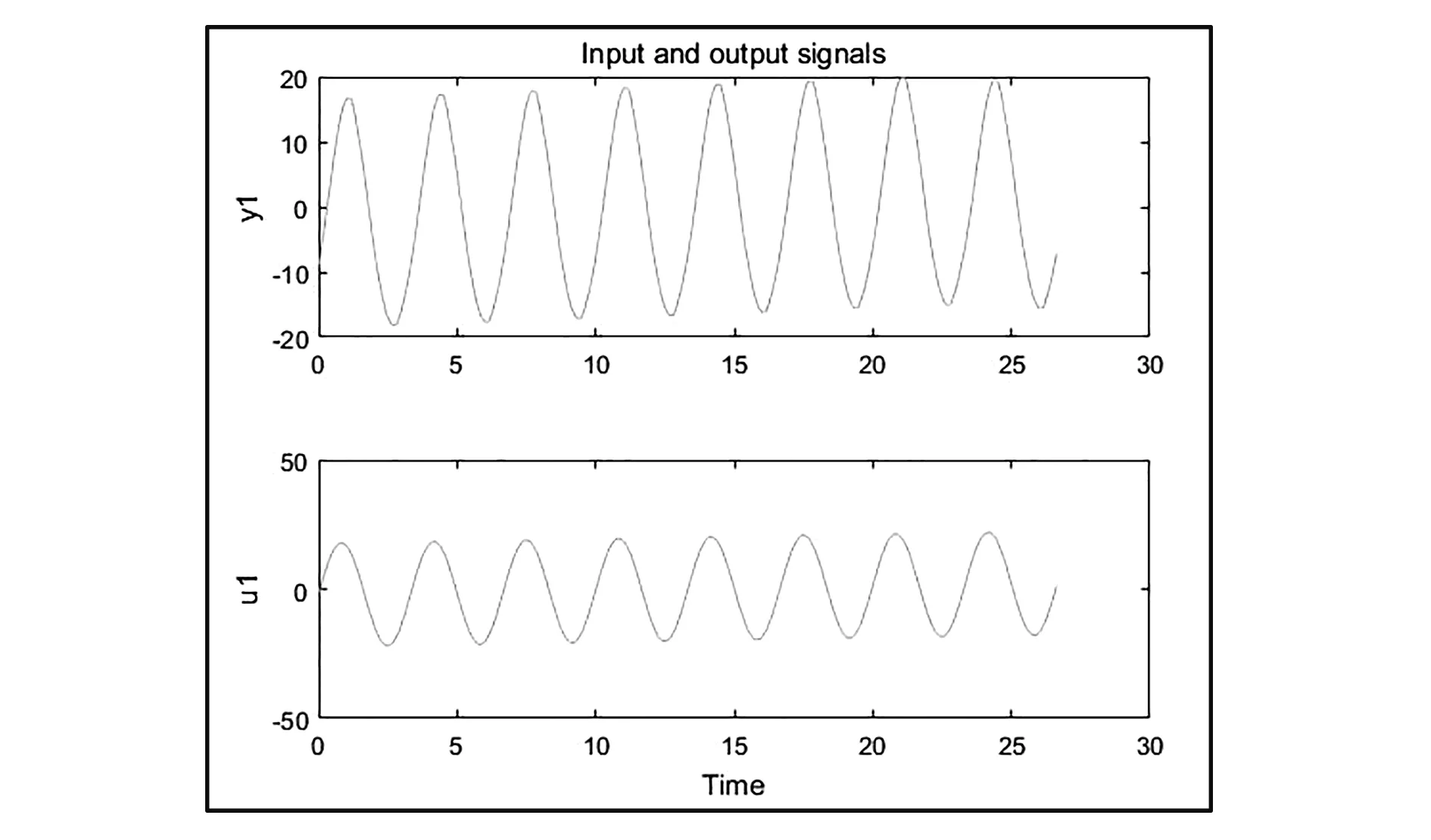
图3 预处理后的输入输出数据
2.3 ARX模型辨识
2.3.1 模型阶次辨识
通过系统辨识工具箱的Order Selection功能进行ARX模型阶次辨识,得到图4所示的ARX模型阶次选择图。条形图显示给定模型参数数量在最优适配情况下的阶次选择情况,Y轴表示预测误差和输出相关性的比率。条图1代表辨识数据与验证数据不同时模型阶次的最优选择(此时na=7,nb=1,nk=1),条图2代表采用Rissanen最小描述长度算法辨识的系统阶次,条图3代表采用Akaike信息准则辨识的系统阶次。从模型阶次预估条形图分析,从na=4,nb=1,nk=1开始,Misfit值趋于平稳,故选择na=4,nb=1,nk=1作为ARX模型辨识的阶次。

图4 ARX模型阶次选择图
2.3.2 模型参数辨识
系统辨识工具箱支持CAR模型的最小二乘参数估计法和辅助变量法参数辨识,本文选取最小二乘参数估计法[5]。
ARX模型为:
A(z(-1))y(k)=z(-d)B(z(-1))u(k)+ξ(k)
(1)
以最小二乘参数估计法进行模型参数辨识,得到的辨识结果为:
(2)
由参数模型式(2)得到系统的连续传递函数为:
(3)
由于arx411模型离散传递函数包含2个负实极点,转换后的连续传递函数阶次由4阶变为6阶。
2.4 ARMAX模型辨识
ARMAX模型为:
A(z(-1))y(k)=z(-d)B(z(-1))u(k)+C(z(-1))ξ(k)
(4)
ARMAX模型将有色噪声加入系统建模,相比ARX模型能更全面描述系统输入、输出和噪声的特性,是描述系统特性最完善的模型。当模型噪声是有色噪声时,最小二乘参数估计的统计特性不具有无偏性和一致性。因此,选用预测误差法(prediction error method,PEM)进行ARMAX模型辨识[6]。
2.4.1 模型阶次辨识
通过armax函数计算na=[2∶6],nb=[1∶4],nc=[1∶4],nk=[0∶2]各阶次系统ARMAX模型的结果,完成240次计算,并进行拟合度对比,其armax模型不同阶次辨识的拟合度对比曲线如图5所示。

图5 armax模型不同阶次辨识的拟合度对比曲线
由图5结果分析,综合高拟合度和低阶优先的选择准则,选取na=3,nb=1,nc=1,nk=1进行ARMAX模型参数辨识。
2.4.2 模型参数辨识
利用系统辨识工具箱,得到基于预测误差法的ARMAX模型辨识结果:
(5)
由参数模型式(5)得到系统的连续传递函数为:
(6)
由于armax3111模型离散传递函数包含1个负实极点,转换后的连续传递函数阶次由3阶变为4阶。
2.5 辨识结果分析
对比arx411和armax3111两种模型的辨识输出结果与验证数据的拟合度,如图6所示,arx411为93.63,armax3111为93.65,armax3111略高。

图6 arx411和armax3111模型辨识输出结果与验证数据的拟合度对比
图7表示两个模型输出残差的自相关函数及输出残差与输入的互相关函数曲线,可以看到,数据未发现野点,都在置信区间内,两种模型都是有效的[7]。
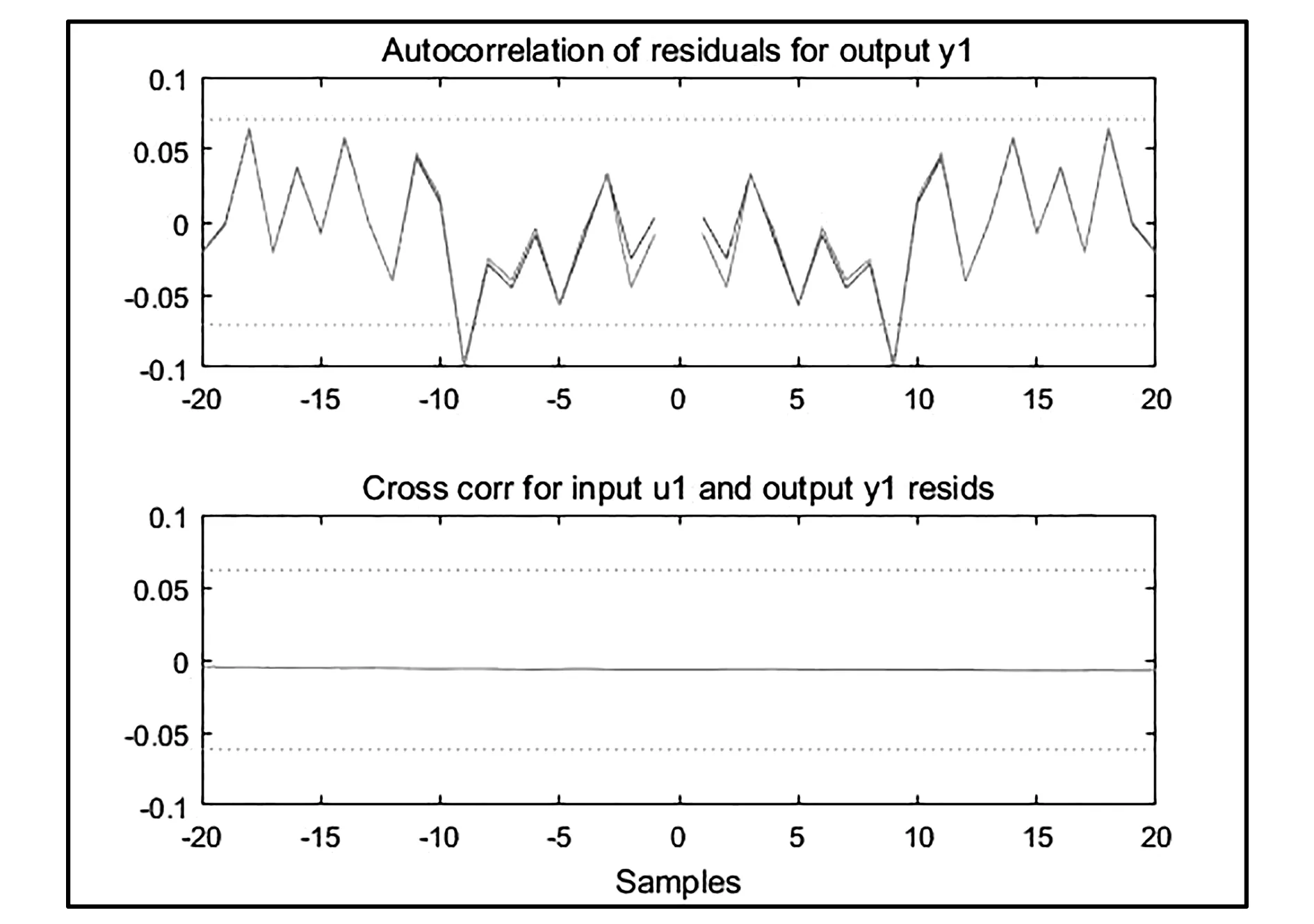
图7 arx411和armax3111模型输出残差的自相关函数及输出残差与输入的互相关函数曲线
通过上述分析,同时便于MOOG控制器参数特性分析,选取阶次较低的ARMAX模型作为电液力反馈控制系统的数学模型。
3 MOOG控制器阻尼环节、前馈环节控制特性分析
上述辨识得到的armax3111传递函数是系统的闭环传递函数,反馈系数为1,闭环传递函数和开环传递函数的关系[8]:
(7)
式中,Φ(s)为系统闭环传递函数;G(s)为系统开环传递函数。
根据式(7),得到电液力反馈控制系统的开环传递函数为:
(8)
根据MOOG控制器用户手册,图1的G2(s)传递函数:
(9)
式中,Td为阻尼环节的时间常数,系统默认值为3.3s。
G3(s)也为一阶高通滤波器结构,则:
(10)
式中,Tf为前馈环节的时间常数,系统默认值为1ms。
3.1 阻尼环节控制特性
由系统仿真知道,未加入控制器校正前,辨识的系统为有静差系统。在单位阶跃输入下,调节系统至较好的上升时间和超调量,并消除系统静差,取比例增益kp=4,积分增益ki=3;不考虑前馈增益影响,取前馈增益kf=0;G2(s)的时间常数Td=3.3s,kd=1,绘制kd变化的参数根轨迹曲线,分析阻尼环节对控制特性的影响。
由上述系数设定,得到系统的开环传递函数G′(s)为:
(11)
代入各参量取值,得到系统的闭环特征方程为:
(4s+3)(3.3s+1)·G(s)+s(3.3s+1+3.3kd)=0
(12)
由上式得到参数kd变化的等效开环传递函数:
(13)
将辨识的系统数学模型G(s)代入上式,绘制G″(s)的零极点分布图和根轨迹曲线,如图8和图9所示。
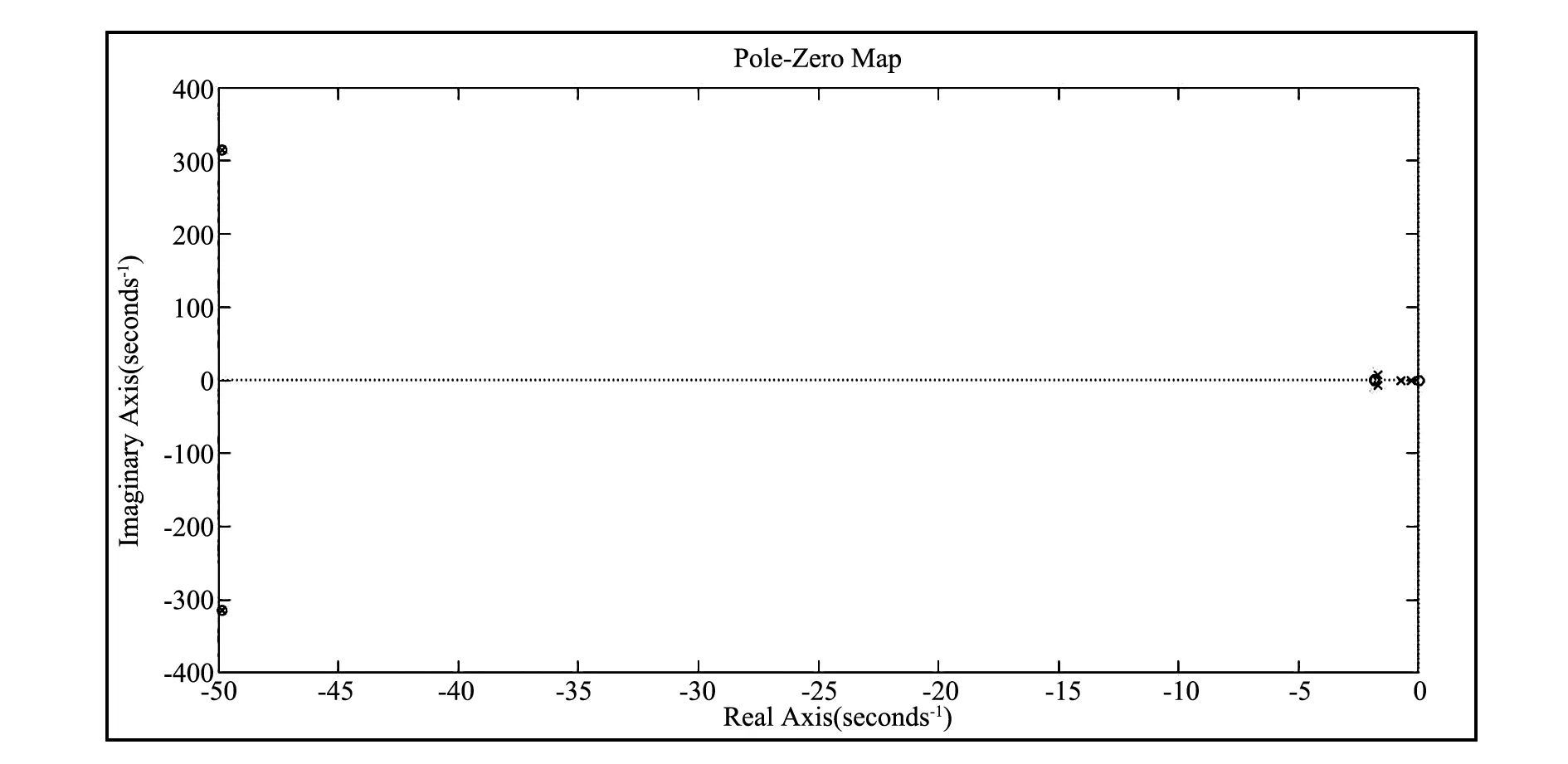
图8 G″(s)零极点分布图

图9 G″(s)根轨迹曲线
由图8、图9分析,忽略离虚轴较远零极点、靠近原点偶极子、负实轴上极点对系统性能的影响,考虑从一对共轭复数极点出发的根轨迹曲线,可以看到,随着阻尼增益kd的增加,系统的闭环极点向实轴上点(-10,0)移动,整个系统的阻尼比不断增加,超调量不断减小;在欠阻尼范围内,系统调节时间不断减小。总之,加入阻尼环节将增强系统的阻尼程度。
3.2 前馈环节控制特性
如图1所示,取kp=4,ki=3,不考虑阻尼环节影响,取kd=0,绘制前馈环节加入前后系统闭环传递函数的bode图,分析前馈环节的控制特性。
未加入前馈环节,对系统的闭环传递函数进行推导。
令比例积分环节:
(14)
系统的闭环传递函数Φ′(s)为:
(15)
加入前馈环节后,系统的闭环传递函数Φ″(s)为:
(16)
式中,令G3(s)的时间常数Tf=200ms;前馈增益kf=100。
绘制Φ′(s)和Φ″(s)的bode图,如图10所示。曲线1和曲线3代表系统加入前馈环节前闭环幅频和相频响应曲线,带宽为11.5rad/s;曲线2和曲线4代表系统加入前馈环节后闭环幅频和相频响应曲线,带宽为48rad/s。可以看到,前馈环节可使系统带宽增大,相角出现超前,谐振峰值变大,可显著提高系统的高频响应。
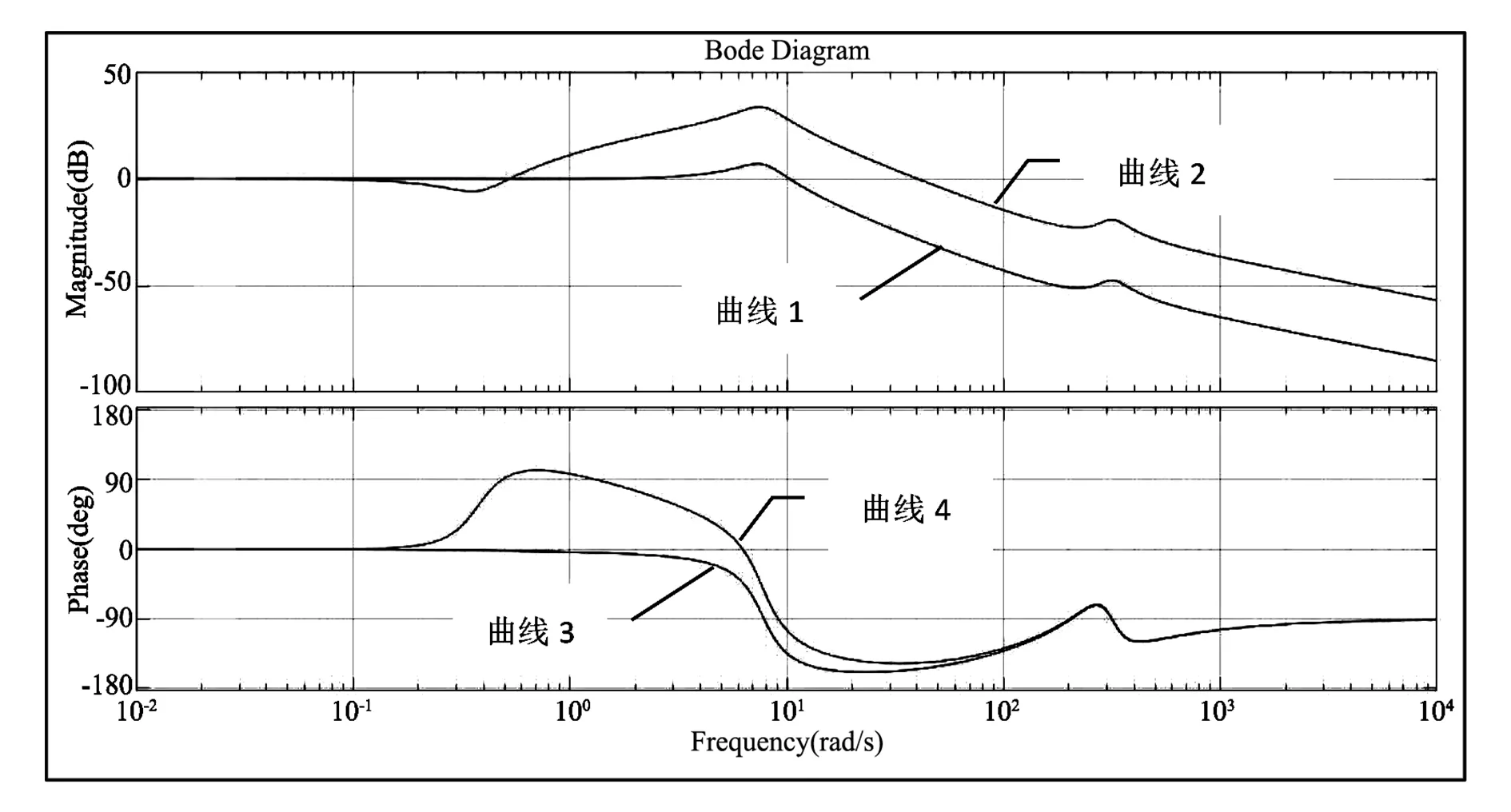
图10 加入前馈环节前后系统闭环bode对比曲线
4 结束语
本文针对电液力反馈控制系统,讨论了系统辨识建模理论和方法,借助MATLAB系统辨识工具箱进行了基于ARX模型和基于ARMAX模型的系统模型结构和模型参数辨识,并进行了模型验证分析。以ARMAX模型辨识结果为对象,通过参数根轨迹法和闭环频率特性仿真分析了MOOG控制器的阻尼环节和前馈环节的调节特性,为控制器的参数整定提供理论依据。

