对流层飞艇总体设计及参数分析

许 军,熊思进

(1.中国电子科技集团公司第三十八研究所,安徽 合肥 230088;2.西北核技术研究所,陕西 西安 710024)

1 引 言

近年来,随着无人飞行器技术的井喷式发展,无人飞艇因其无人化、滞空时间长、安全性高、可低速飞行等优势,逐渐得到广泛应用。特别是在战场侦察监视、民用货运、遥感遥测等领域,无人飞艇成为近些年低速无人飞行器的一个重要研究方向和研究热点[1-4]。

飞艇是一种低速浮空飞行器,主要利用气囊中的氦气和空气等气体产生浮力。伴随着无人技术的发展,低空无人飞艇逐渐得到推广和应用,因此对于无人飞艇的总体设计研究至关重要。

无人飞艇的总体参数设计会影响飞艇的总体性能指标,如何在不同参数中选择最优的参数值也成为研究重点。与其他飞行器相比,飞艇的载重能力、巡航速度、飞行高度、续航时间、供电能力等至关重要。通过分析可知,不同的设计参数(飞行高度、飞行速度、载重能力等)和环境因素(如大气温度、大气压力等)对飞艇系统总体指标和性能影响较大,因此,深入分析不同参数对无人飞艇总体性能的影响是十分必要的。同时,掌握不同参数对无人飞艇总体性能的影响规律对理论方法研究和工程设计分析具有较好的指导意义[5-9]。

2 总体设计

针对任务载荷能力150kg、续航时间10h、飞行高度3200m等要求,开展低空飞艇总体设计,分析不同的总体设计参数对飞艇总体性能的影响,重点从浮力特性分析、速度特性分析、续航特性分析、上升/下降特性分析等方面进行飞艇性能特性计算与参数分析研究。

3 浮力特性分析

根据理想气体状态方程和空气、氦气等气体参数,按照浮重平衡特性,可以计算出飞艇的总浮力、氦气和空气重量,然后计算出飞艇的静浮力。图1给出了不同体积下的总浮力,可以看出,3200m高度下,2000m3时的总浮力为1781.4kg,满足飞艇空机重量、任务载荷重量、燃油量、静浮力等要求,故选择2000m3作为设计体积。

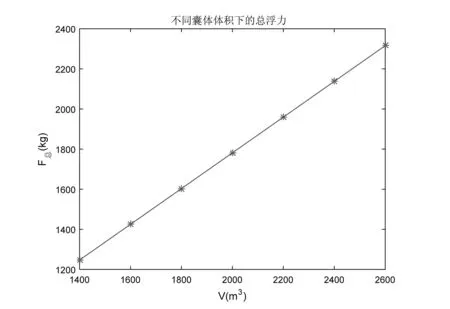
图1 不同体积下的总浮力

氦气纯度对飞艇的总浮力和静浮力有影响,通过计算不同氦气纯度下的总浮力和静浮力,可得到氦气纯度对浮力特性的影响,进而可根据氦气纯度综合评估飞艇的飞行性能特性。图2给出了3200m高度下不同氦气纯度下的总浮力、静浮力的计算结果。总浮力与飞艇体积相关,而静浮力随着氦气纯度的变化会发生变化。随着氦气纯度的增大,静浮力也增大。

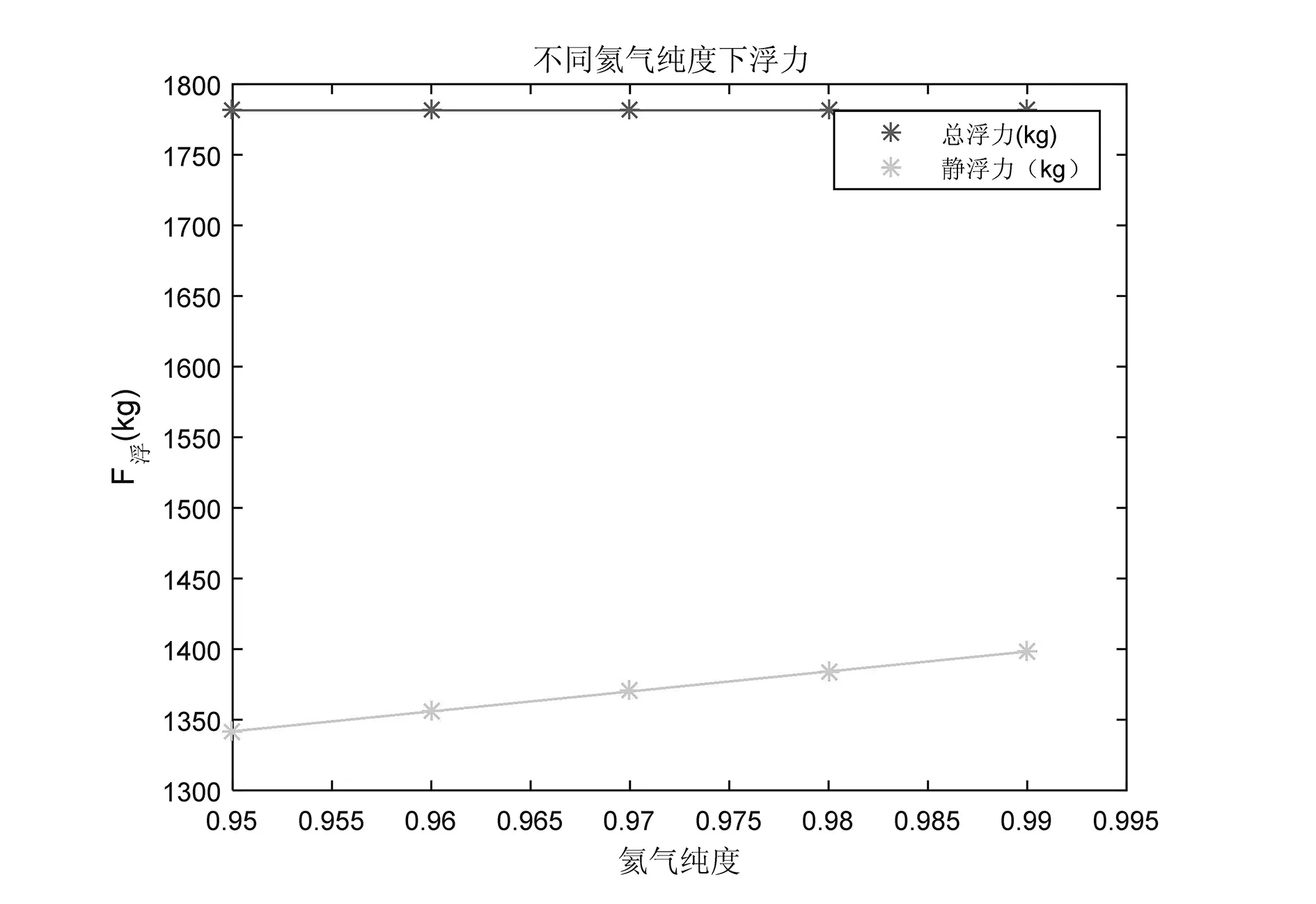
图2 不同氦气纯度下的浮力变化

飞艇在不同高度下的载荷能力是不同的,研究载重能力随高度的变化趋势可为飞艇性能设计提供依据。图3给出了不同高度下飞艇的最大载重能力,可以看出,随着任务高度的降低,载重能力逐渐增大。

不同的地面温度和不同的气囊差压对飞艇的浮力特性也有影响。图4和图5分别给出了不同地面温度、不同差压下的总浮力和静浮力,可以看出,随着地面温度的升高,总浮力和静浮力下降;差压对浮力的影响不大。

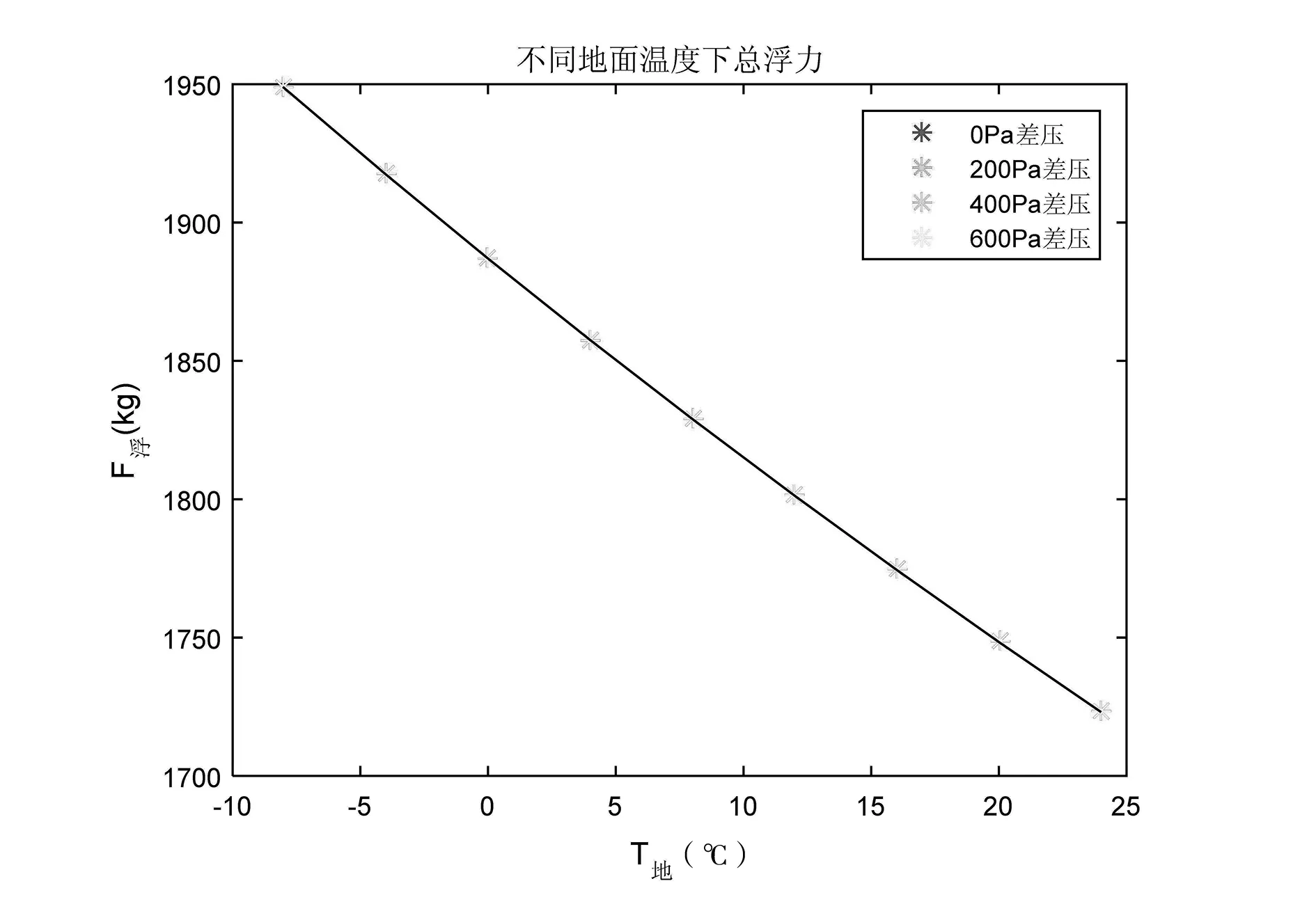
图4 不同地面温度、不同差压下的总浮力

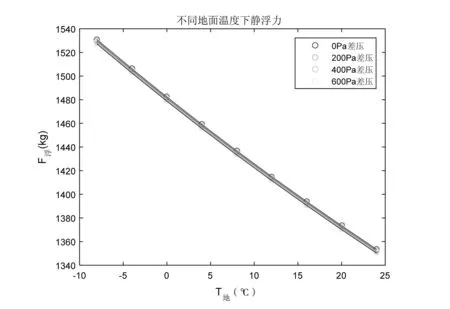
图5 不同地面温度、不同差压下的静浮力

4 速度特性分析

速度包线决定了飞艇的飞行性能。飞艇的速度特性主要包括最大飞行速度、最小飞行速度等。其中,最小飞行速度主要由飞艇的气动特性、高度等决定,最大飞行速度与飞行选择的发动机、飞行阻力特性、高度等有关。

依据文献[10]中对飞艇阻力系数特性的分析结果,图6给出了不同阻力系数时飞艇在最大速度70km/h的推进功率特性[11,12]。可以看出,同等高度下,随着阻力系数的增大,推进功率也增大。地面0海拔时,当阻力系数在0.04～0.05之间变化,推进功率从28.59kW～35.74kW之间变化。同等阻力系数时,随着高度的增大,推进功率下降。阻力系数为0.04时,高度从地面到3200m变化,推进功率为28.59kW～20.79kW。

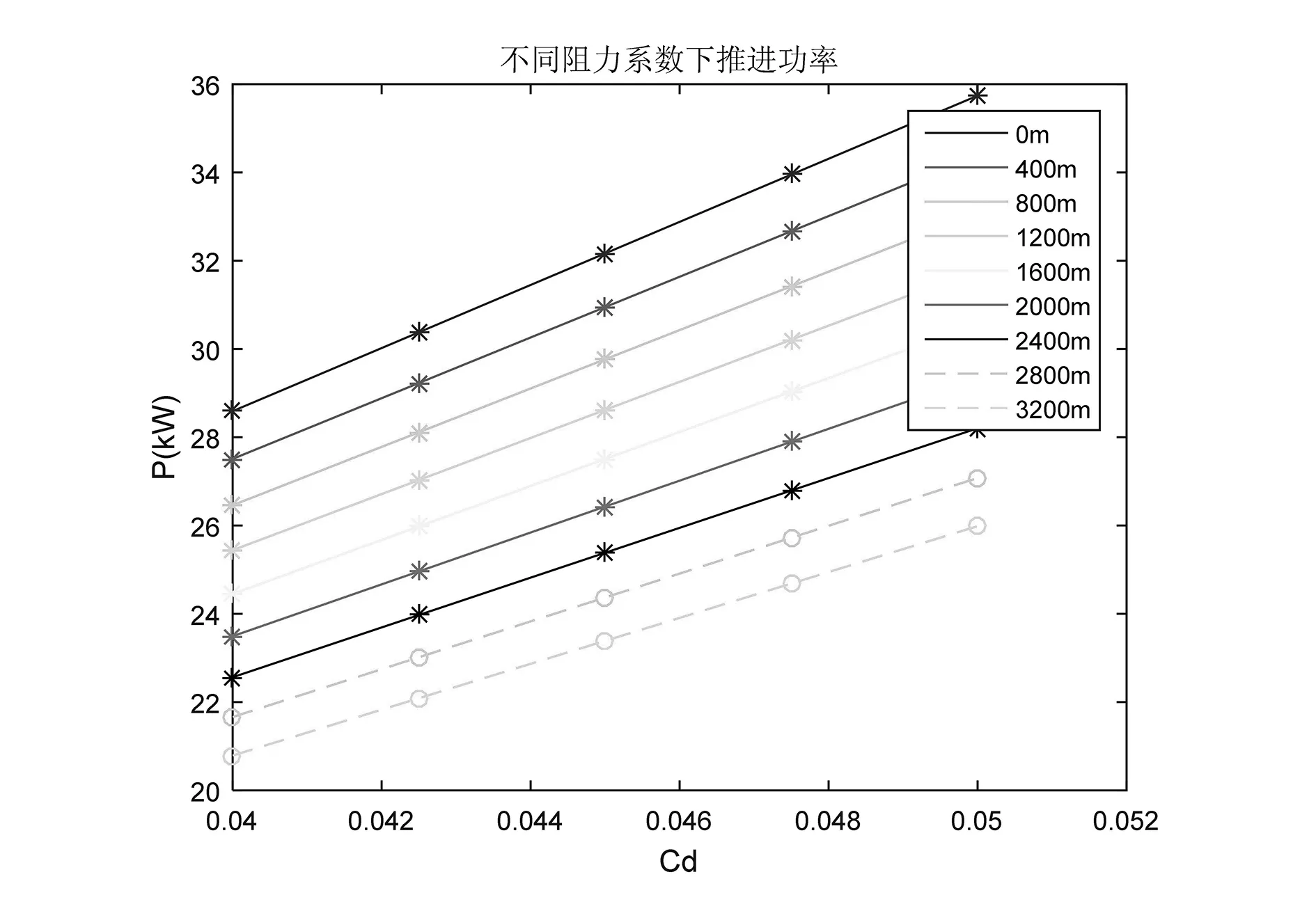
图6 不同阻力系数下推进功率随高度的变化

飞艇飞行过程中,不仅需要发动机输出推进功率以保证飞艇飞行,飞艇艇上机载设备的工作也需要发动机驱动发电机产生额外的功率。因此,对发动机功率需求的设计,还需要进一步分析艇载平台用电功率特性的影响因素。图7给出了不同平台用电功率需求下的海平面需用功率,可以看出,相同海拔条件下,随着平台用电功率需求的增大,海平面需用功率也增大。0m高度下,平台用电功率为2kW时,海平面需用功率为50.01kW。同等平台用电功率下,随着海拔高度的增大,海平面需用功率也增大。3200m高度下,平台用电功率为4.5kW时,海平面需用功率为59.85kW。

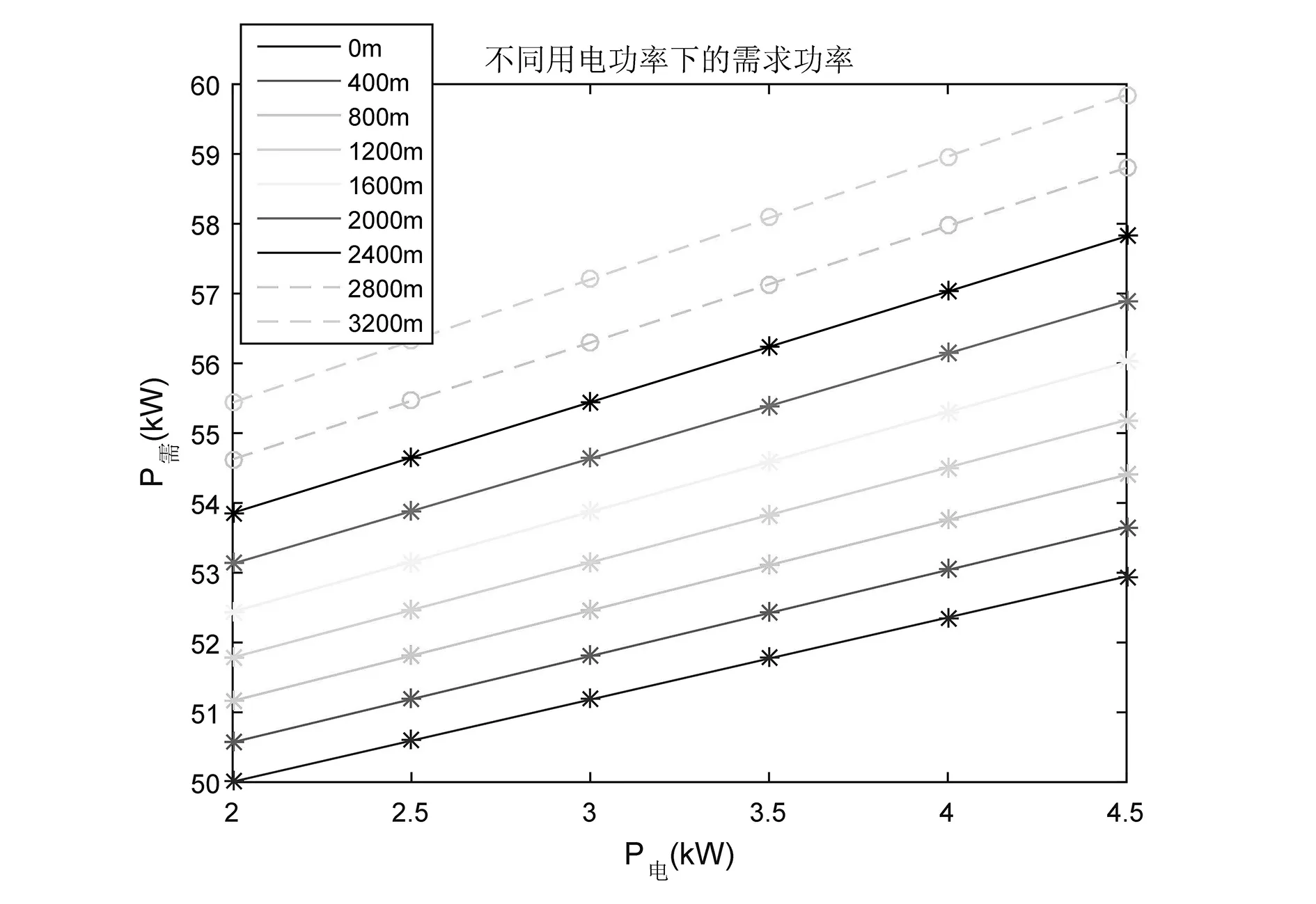
图7 不同用电功率下的海平面需用功率变化

结合发动机输出功率需求及对流层飞艇的双发特性,对比分析Rotax活塞式发动机特性。选取某Rotax式活塞发动机,该发动机在2000r/min和最大速度要求下,输出功率接近50kW,满足对流层飞艇双发功率的要求。结合发动机输出功率衰减特性开展飞艇最大速度特性的计算分析,不同高度下的最大速度特性如图8所示。可以看出,同等高度下,随着用电设备功耗的增加,最大速度值减小。在2kW用电设备功耗、3200m高度时,最大飞行速度为79.89km/h。同等用电功耗条件下,随着海拔高度增大,最大速度下降。在4.5kW用电功耗下,飞行高度3200m时,最大速度为78.66km/h。

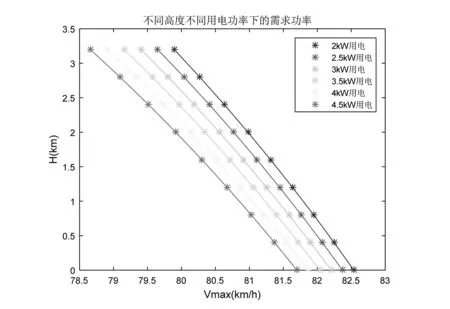
图8 不同高度下的最大速度特性

根据飞艇的气动特性、飞艇的面积、剩余浮力等参数,利用文献[13]中的方法,计算不同高度和不同剩余浮力状态下的最小速度特性。图9和图10分别给出了不同高度和剩余浮力状态下的失速速度、最小速度变化曲线。

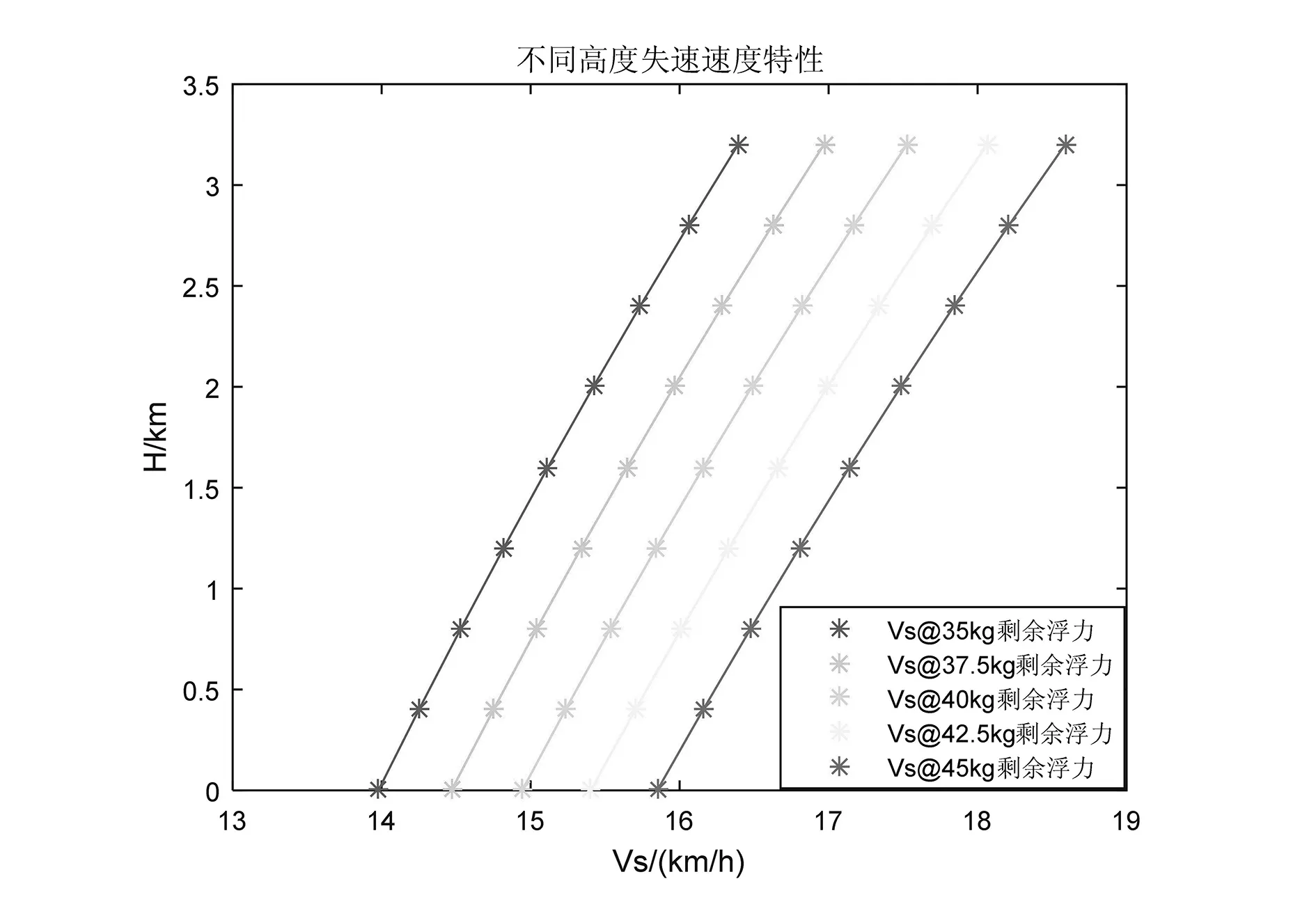
图9 不同高度下的失速速度特性

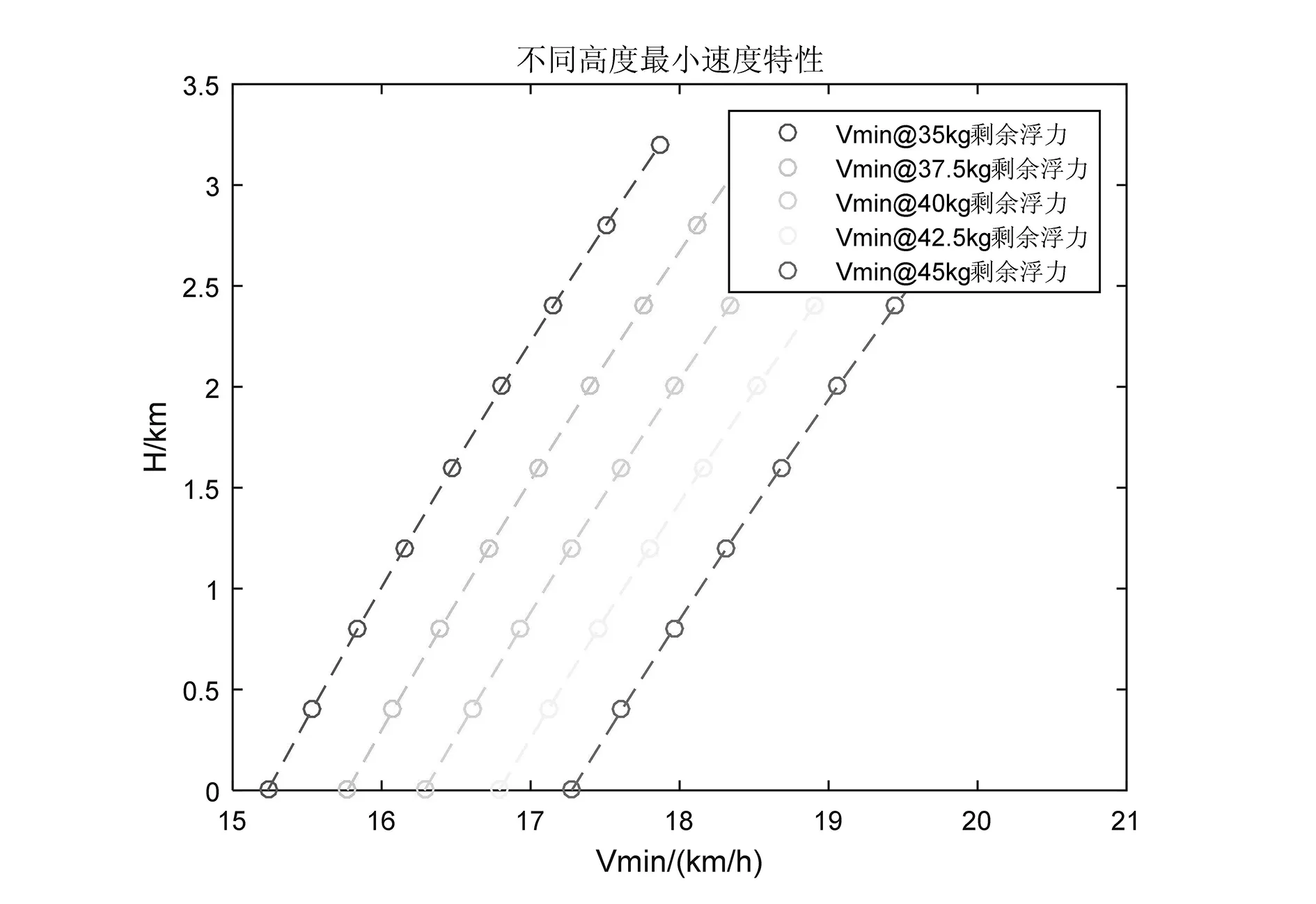
图10 不同高度下的最小速度特性

从图9可以看出,同等剩余浮力状态下,随着海拔高度的增大,飞艇的失速速度呈现增大趋势。在40kg剩余浮力状态下,0km高度的失速速度为14.94km/h,3.2km高度时失速速度为17.53km/h。从图10可以看出,同等剩余浮力状态下,随着海拔高度的增大,飞艇的最小速度均呈现增大趋势。在40kg剩余浮力状态下,0km高度的最小速度为16.29km/h,3.2km高度时的最小速度为19.10km/h。

5 耗油特性分析

根据飞行任务阶段不同、发动机不同阶段耗油特性进行续航时间的计算分析。飞艇飞行任务剖面包括起飞、爬升、巡航、下降、降落等过程,在起飞、爬升、下降、降落等过程中,任务载荷基本不工作。因此,对飞艇飞行续航时间和油量影响较大的是巡航阶段,巡航阶段需要考虑不同的任务功耗、飞行高度等对耗油量的影响。因此,通过分析巡航阶段不同任务功耗、飞行高度特性可为续航时间设计提供参考。

图11给出了不同高度、不同用电功耗下的巡航耗油量,可以看出,同等用电功耗下,随着海拔高度的增大,巡航耗油量也增大;同等海拔高度下,随着用电功耗的增大,巡航耗油量也增大,2kW用电负载0km高度时耗油量为17.66kg/h。

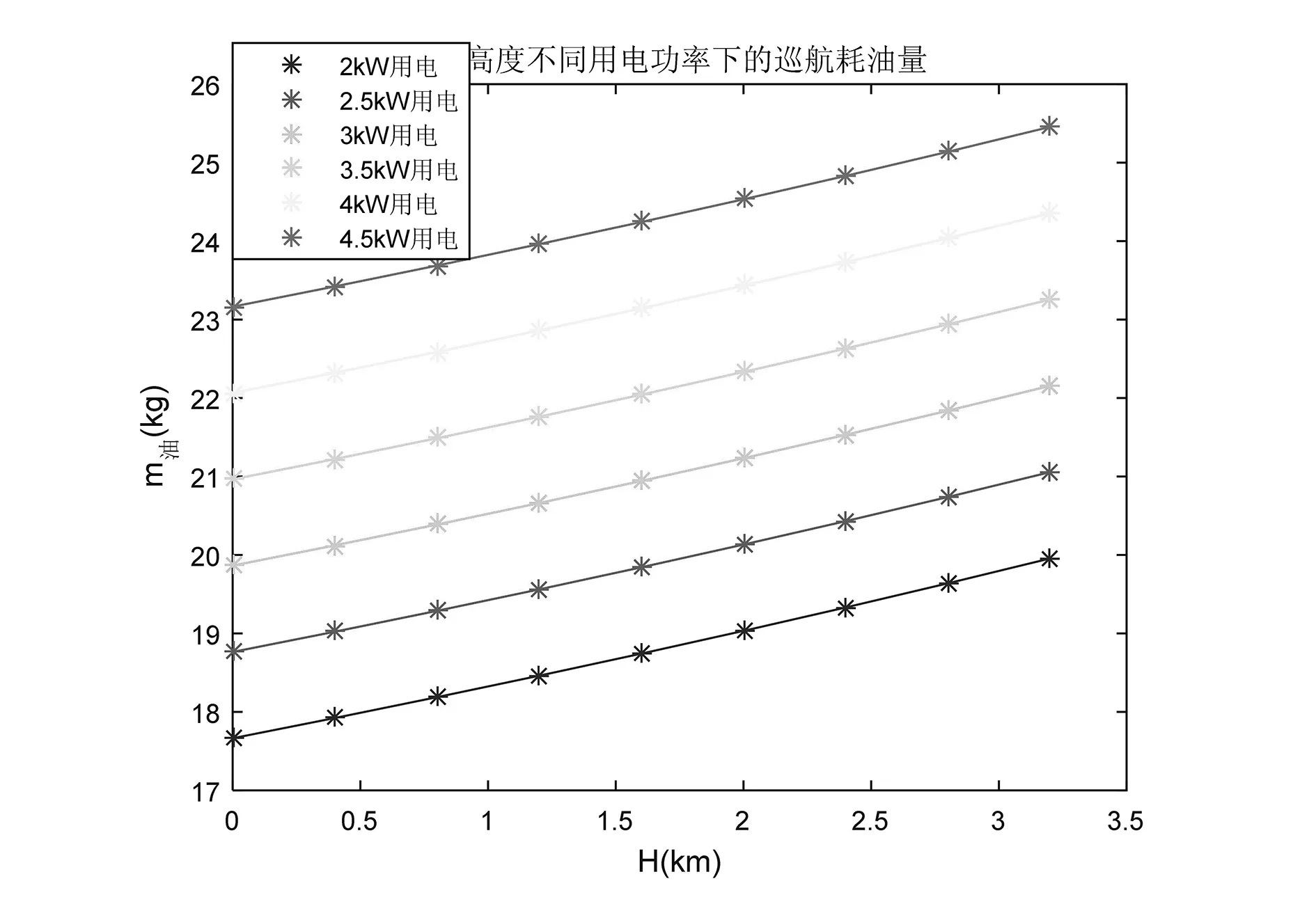
图11 不同高度、不同用电功耗下每小时巡航耗油量

图12给出了不同高度、不同剩余浮力下的巡航耗油量,可以看出,同等剩余浮力下,随着海拔高度的增大,巡航耗油量增大;同等高度下,随着剩余浮力的增大,巡航耗油量也增大。在35kg剩余浮力、0km高度时,耗油量为17.66kg/h。

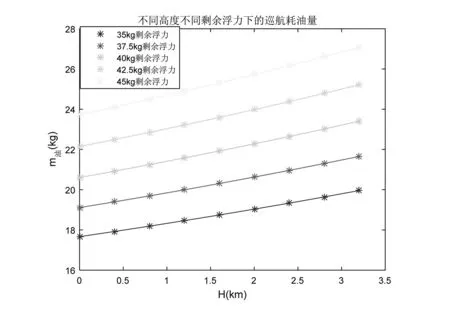
图12 不同高度、不同剩余浮力下每小时巡航耗油量

6 上升/下降特性分析

飞艇在上升、下降过程中,囊体内的压力会发生变化。为了保证飞艇囊体结构的完整性,需要对飞艇上升、下降过程中不同气囊间的压力进行调节。分析不同的参数对压力特性的影响,对飞艇设计和试验至关重要。

基于文献[14,15]中相关飞艇排气流量和阀门特性计算方法,计算不同上升/下降速度时进排气流量。进排气流量随上升/下降速度的变化如图13所示,可以看出,同等高度下,随着上升/下降速度的增大,进排气流量也增大。地面0海拔、3m/s的上升/下降速度时,进排气流量为0.576m3/s。同等上升/下降速度下,随着高度的增大,进排气流量增大。在3m/s的上升/下降速度、高度3200m时进排气流量为0.673m3/s。

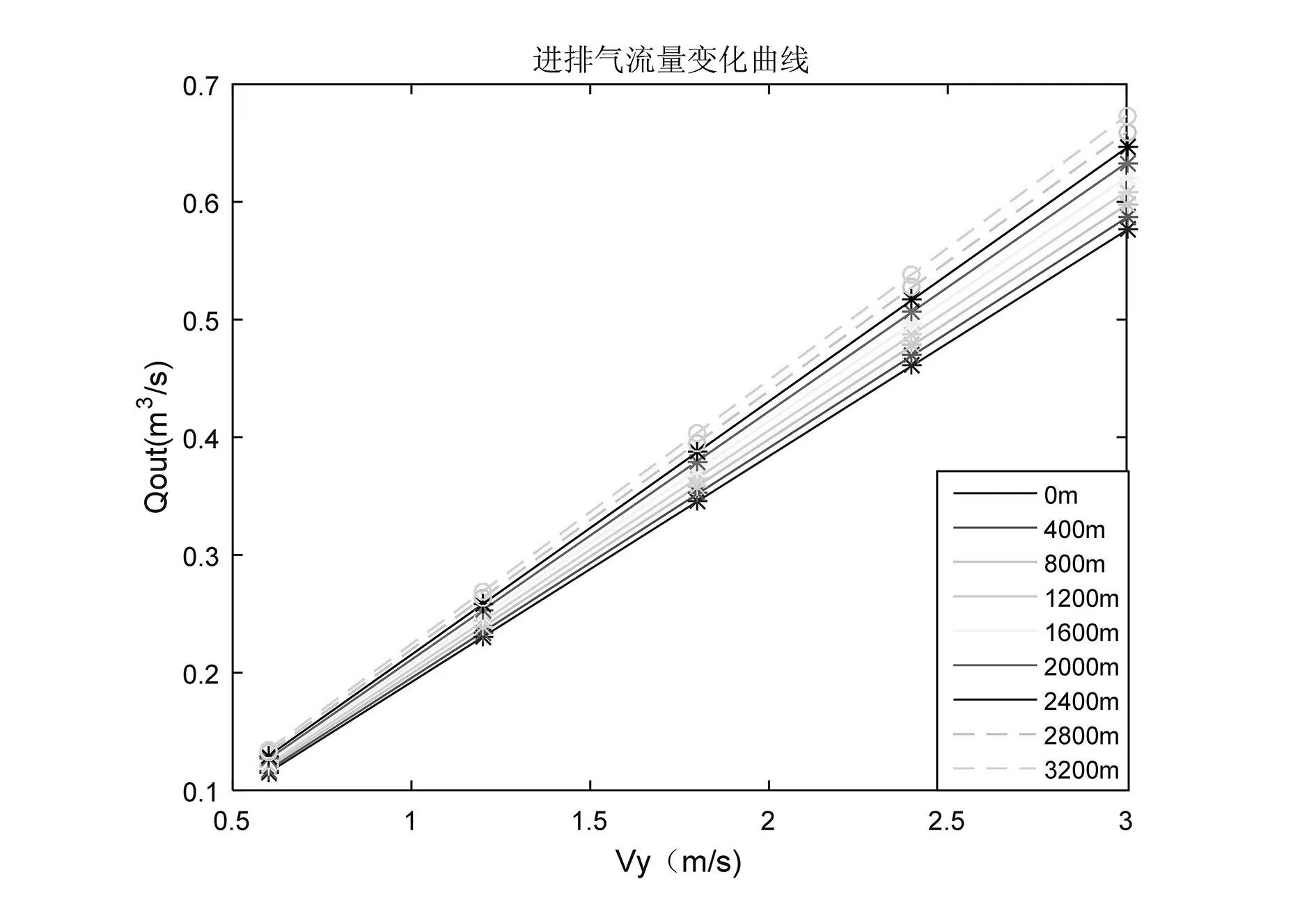
图13 进排气流量随上升/下降速度的变化

根据相关文献[14,15]资料中的计算方法,计算出不同囊体差压下的空气阀门流通面积,如图14所示。可以看出,同等高度下,随着囊体差压的增大,空气阀门的流通面积减小。0海拔、囊体差压为300Pa时,空气阀门的流通面积最大为0.064m2。同等囊体差压下,随着海拔高度的增大,空气阀门的流通面积变化不大。在300Pa差压、海拔高度3200m时,空气阀门流通面积最大为0.066m2。

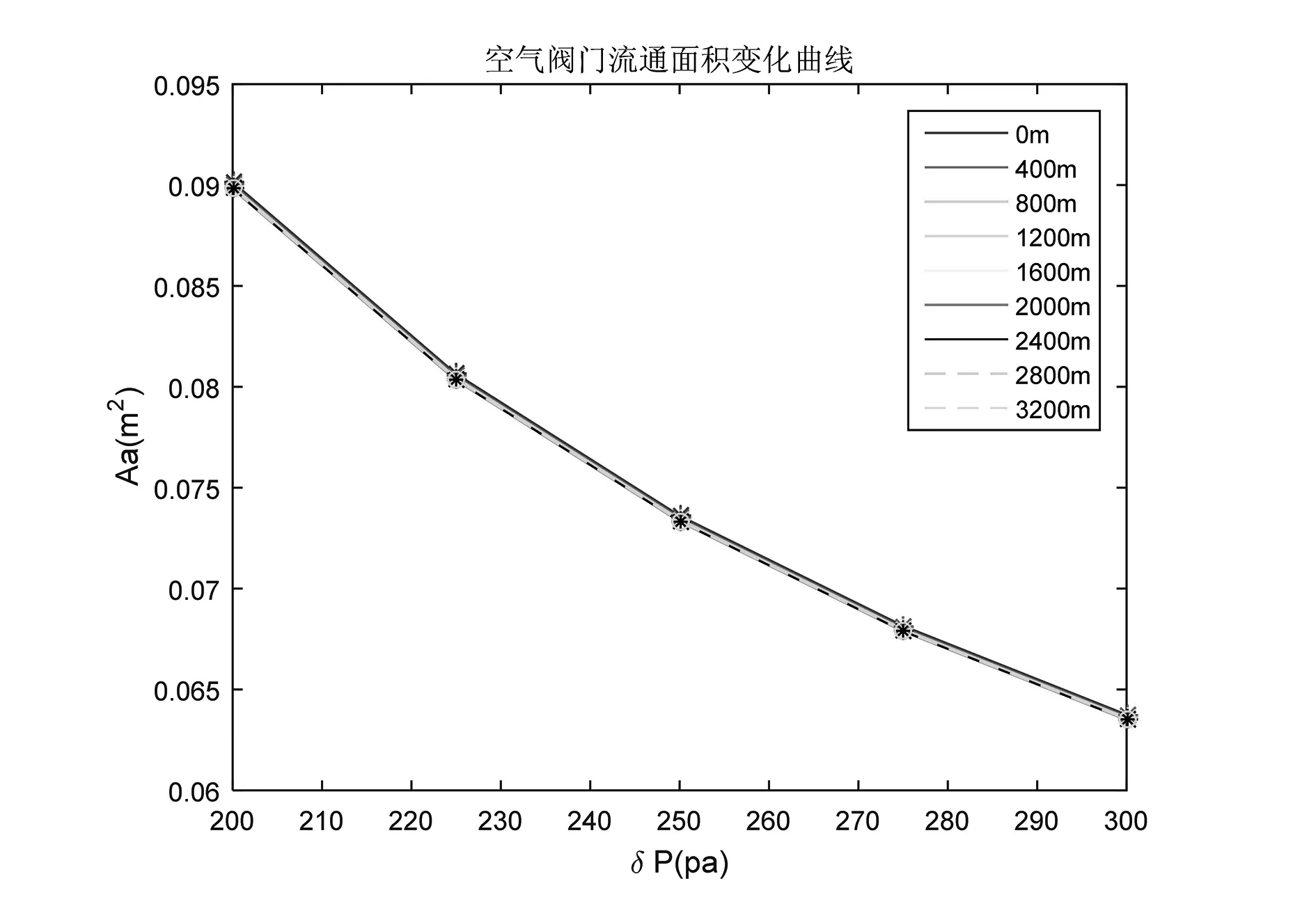
图14 空气阀门流通面积随囊体差压的变化

不同囊体差压下氦气阀门的流通面积如图15所示,可以看出,同等高度下,随着囊体差压的增大,氦气阀门的流通面积也增大。0海拔、囊体差压为300Pa时,氦气阀门的流通面积最大为1.523m2。在同等囊体差压下,随着海拔高度的增大,氦气阀门的流通面积也增大。300Pa差压、海拔高度3200m时,氦气阀门流通面积最大为1.786m2。

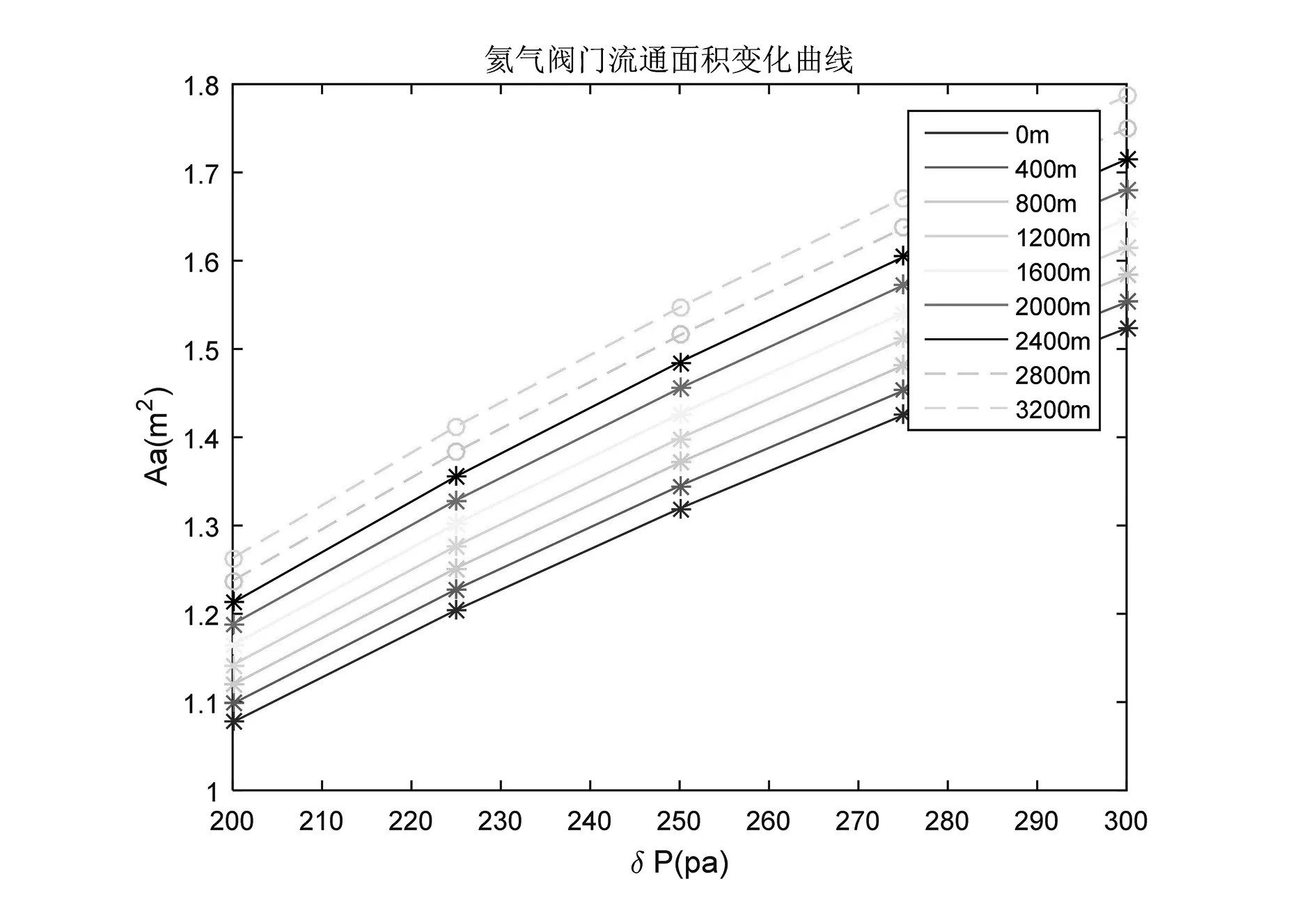
图15 氦气阀门流通面积随囊体差压的变化

通过氦气阀门流通面积的计算,可进一步分析飞艇的最大下降能力,即当氦气阀门开启时,可通过飞艇的下降速度来判断其最大下降能力。飞艇最大下降速度示意图见图16,可以看出,同等高度下,随着囊体差压增大,飞艇最大下降速度也增大。0海拔、囊体差压为300Pa时,最大下降速度为7.935m/s。同等囊体差压下,随着海拔高度的增大,飞艇最大下降速度变化不大。300Pa差压、海拔高度3200m时,最大下降速度为7.962m/s。

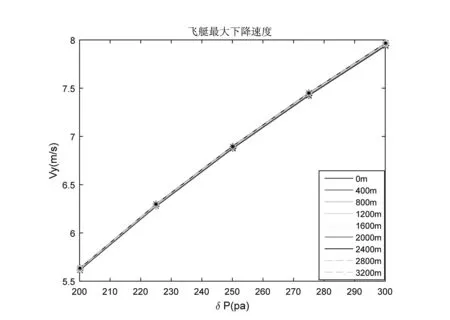
图16 飞艇最大下降速度示意图

7 结 论

通过本文的研究,得出的主要结论如下:

(1)氦气纯度和囊体差压对总浮力、剩余浮力的影响不同。

(2)阻力系数和飞行高度对推进功率均有影响。同等高度下,随着阻力系数的增大,推进功率增大;同等阻力系数时,随着高度的增大,推进功率下降。

(3)用电功耗与阻力系数对发动机功率需求有影响,且呈正相关趋势。

(4)剩余浮力对最小速度、失速速度有影响,且呈正相关趋势。

(5)用电功耗、剩余浮力对巡航高度下的耗油量有影响,且呈正相关趋势。

(6)氦气阀门、空气阀门流量与囊体差压有关,氦气阀门流量与囊体差压呈正相关趋势。

(7)最大下降速度与氦气阀门流量有关,且呈正相关趋势。