基于灰色马尔可夫链的航天器热平衡温度估计研究

李云恒

(北京空间机电研究所,北京 100094)

1 引 言

航天器热平衡温度估计结果是影响装置热设计试验时间、费用和精度的重要依据,因此,合理地选择合适的温度稳定性准则是确保试验精度、控制试验时间和成本的重要依据。我国在GJB 1033A-2005文件中提出了明确的规定,即航天器热平衡测点温度在连续4h内的波动值控制在±0.5℃以内时,可以输出此时航天器热平衡测点温度,并认为在此种条件下航天器达到热平衡温度[1]。而美国则在NASA-SP-2007-3406文件中规定,当航天器热平衡温度的最大热时间常数温度、预期外推的稳态温度值与实际测量的温度值之间的差距小于3℃,或航天器温度有效变化率小于1℃/h时,定义此时的温度值为航天器热平衡温度。

通过上述分析可知,发达国家较早便引进了温度外推的概念。为实现我国航空航天研究成果与国际研究成果接轨,各大科研院所加大了对航天器热平衡试验的投入,并将工作的重点置于航天器热平衡温度估计与预测研究方面[2]。但由相关单位阶段性工作的反馈可知,现有的方法在实际应用中无法实现对航天器热平衡温度的精准预测,导致空间环境模拟试验处于滞后状态。为解决此方面问题,本文引进灰色马尔可夫链,设计一种针对航天器热平衡温度的全新估计方法,旨在通过此次设计,提高热平衡温度估计的精确度。

2 建立航天器热平衡温度数学模型

为实现对航天器热平衡温度的估计,突出航天器的耦合传热特性,将其分解成内外壳集成式机械结构,构建航天器热平衡交换模型,如图1所示[3]。

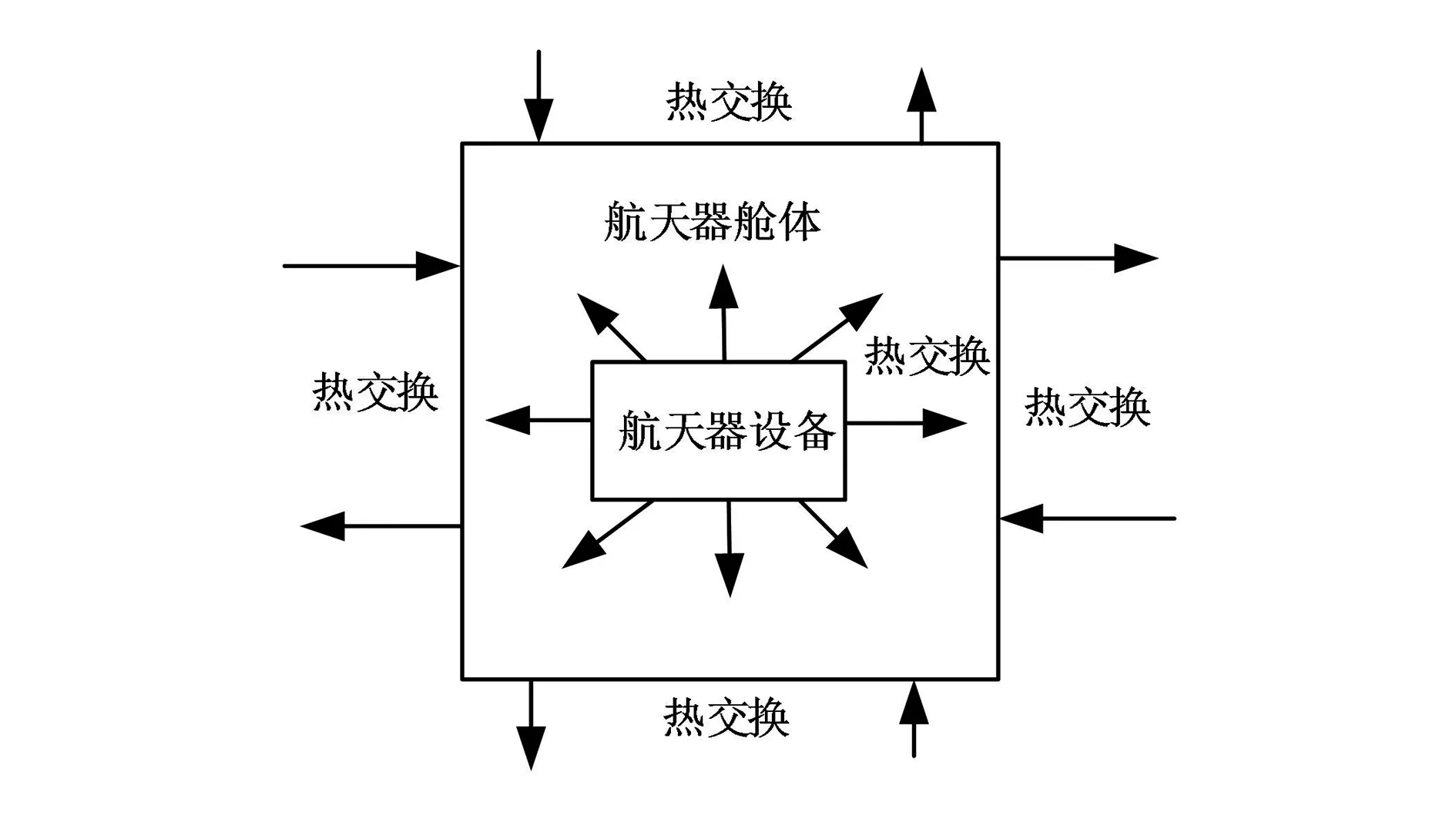
图1 航天器热平衡交换模型

控制在航天器热交换过程中设备与舱体之间的温度,此过程见式(1)。

(1)

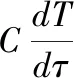
在航天器热平衡相对稳定阶段,对R(T14-T24)进行温度的换热线性计算,此过程见式(2)。

R(T14-T24)=R4Tm3(T1-T2)

(2)

式中,Tm表示温度参数。

Tm=(T1∞-T2∞)/2

(3)

式中,T1∞表示T1的平衡值;T2∞表示T2的平衡值。

在此过程中,应明确在|1-T1/T2|≤0.2的条件下,上述计算公式满足航天器热平衡温度数学模型验证需要。在此基础上,对航天器热交换过程中的舱体热辐射项进行Taylor展开处理,通过此方式,可以得到航天器热平衡温度的一阶导数值[4]。根据所求得的已知值,将其用于航天器热平衡交换过程中,即可得到航天器热平衡温度数学模型。

3 基于灰色马尔可夫链建立温度状态转移函数

完成上述设计后,引进灰色马尔可夫链,建立温度状态转移函数。在此过程中生成一个3层架构、满足数据前向传输的过程热传递模型,其拓扑结构如图2所示。

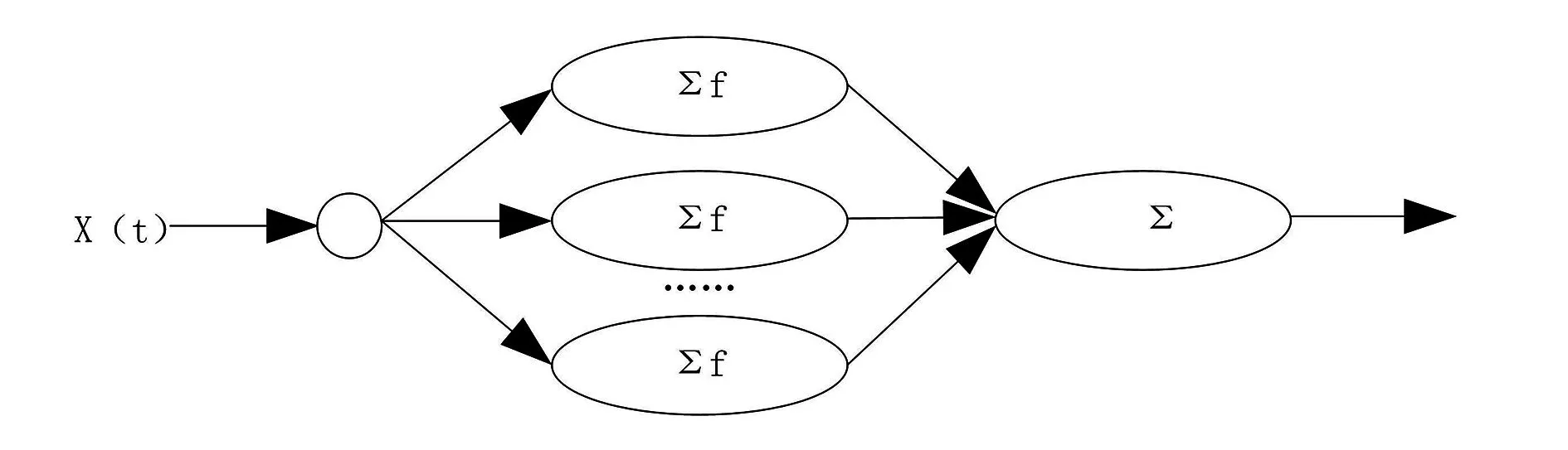
图2 3层架构满足数据前向传输的过程热传递模型

图2中,X(t)表示前端输入值,即航天器初始化温度值;∑f表示求和。热传递过程中,输入层中有1个节点,隐藏层包含若干个处理神经元,可在空间上对输入数据进行权重聚集和时间积累处理,输出层只有1个常规神经元,可整合隐藏层处理的结果,以此种方式,即可实现对航天器温度状态的输出。为实现对此过程中温度状态转移行为的描述,可根据航天器的当前热平衡状态,依据航天器温度的未来变化趋势,对其进行正向估计[5]。对航天器温度状态发生转移的概率进行计算,计算公式如下:

(4)

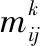
4 航天器热平衡温度估计值校正

在上述设计内容的基础上,进行航天器热平衡温度估计值的校正,此过程如图3所示。

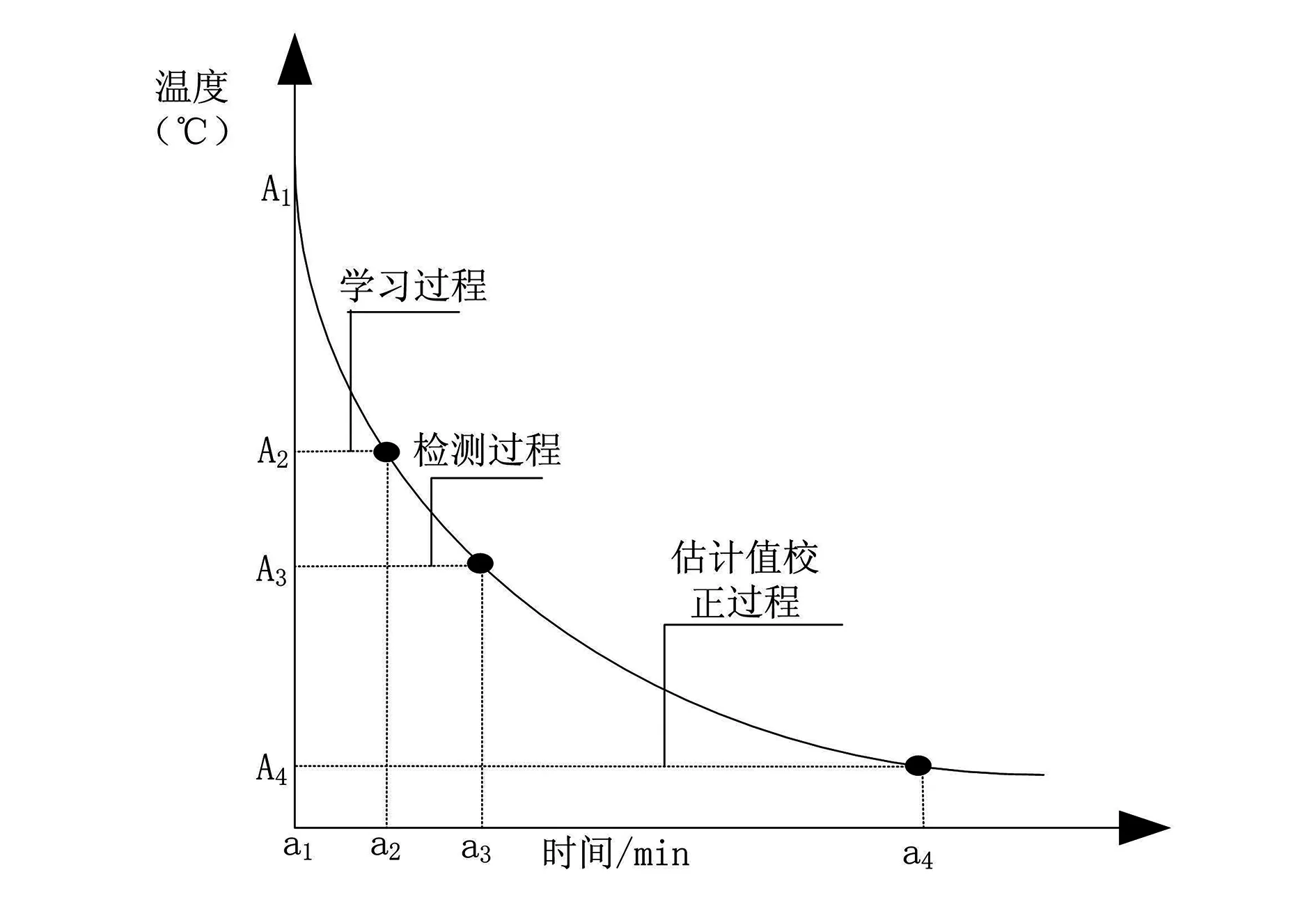
图3 航天器热平衡温度估计值校正过程

从图3可以看出,航天器热平衡温度估计值校正过程由3个步骤构成,分别为学习过程、检测过程与估计值校正过程。检测过程也可称为估计过程,通常情况下,航天器热平衡温度估计过程截止到(A3,a3),但此时段下得到的航天器热平衡温度值可能与实际值存在一定的偏差,即温度值不满足稳定性判定依据(判定依据为航天器热平衡测点温度在连续4h内的波动值控制在±0.5℃以内)。因此,在估计航天器热平衡温度时,需要增加一个校正步骤,通过对现有温度值的持续训练与检测,进行航天器热平衡温度值的调节,直到最终温度值满足稳定性判定依据。通过这种方式实现对航天器热平衡温度估计值校正,完成基于灰色马尔可夫链的航天器热平衡温度估计研究,为空间环境模拟试验及相关工作的规范化实施提供进一步的指导与帮助。

5 对比试验

为实现对本文设计的基于灰色马尔可夫链的航天器热平衡温度估计方法在实际应用中估计结果精度的检验,下述将以北京空间机电研究所为试点单位,选择某具有代表性的航天器系统作为空间环境模拟试验对象,设计航天器热平衡温度估计试验。对航天器技术参数进行描述,相关内容见表1。

表1 航天器技术参数

掌握试验对象的基本运行条件后,分析航天器舱体温度随时间变化的规律,此过程如图4所示。

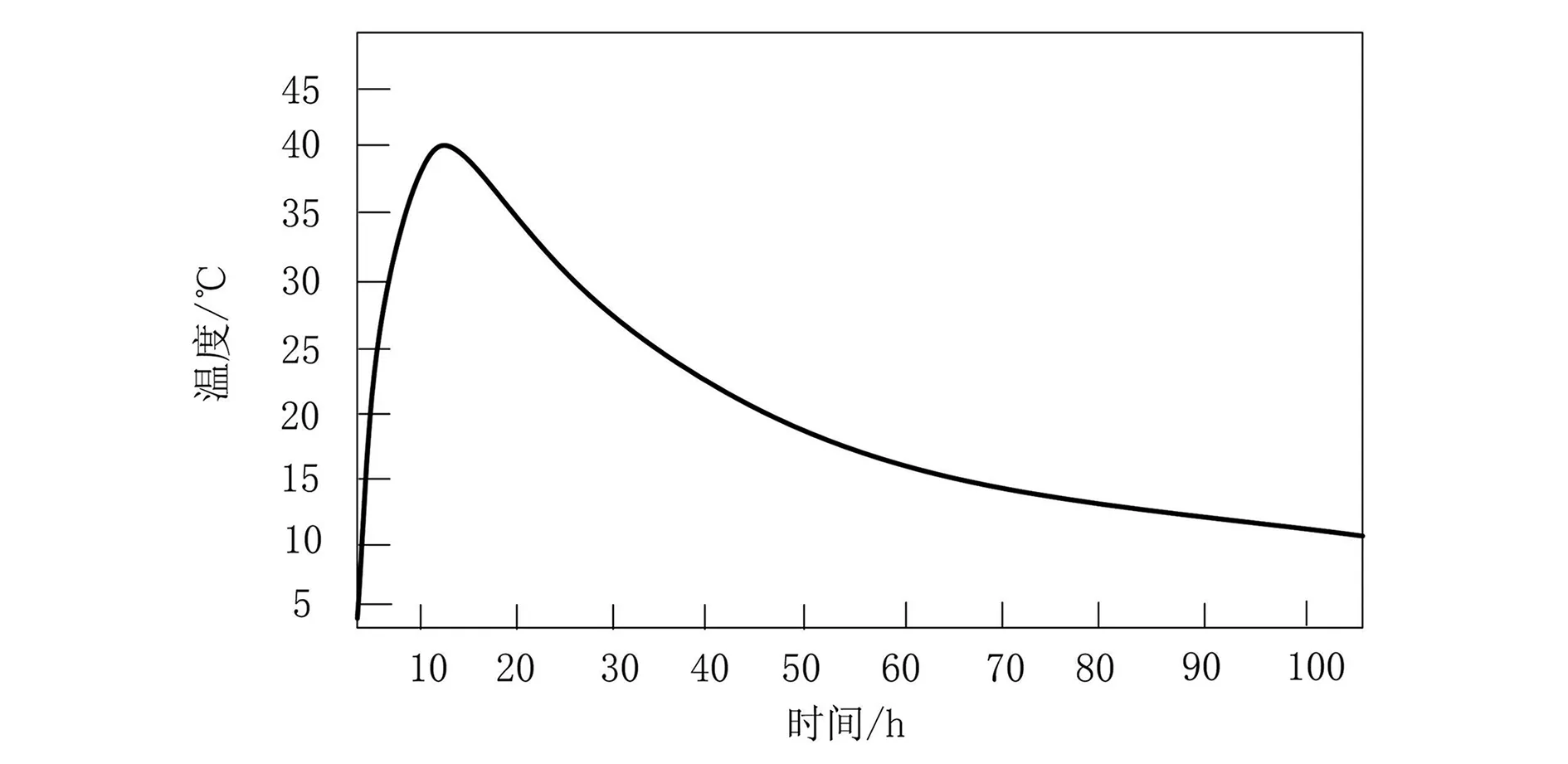
图4 航天器舱体温度随时间变化的规律

航天器设备启动后,舱体温度快速上升。由于设备和舱内的耦合散热,舱内温度上升到一个极限值后,舱内热量逐渐消散,温度逐步下降,最终达到一个相对稳定、单调状态。在此基础上,对航天器设备与舱体温度变化率趋势进行分析(温度稳定变化时段),此过程如图5所示。

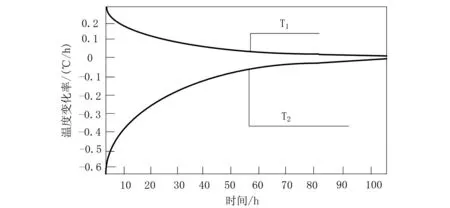
图5 温度变化率在稳定阶段随时间的变化趋势

图5中,T1=T2=航天器在平衡状态下的初始化可测得温度。在温度变化率接近均衡的条件下,航天器设备与舱体温度变化率逐步趋近于0℃/h。与此同时,热平衡的温差则逐渐下降,达到热均衡状态。为实现对此过程中航天器热平衡温度的估计,在掌握空间环境模拟试验标准与航天器热平衡试验步骤后,使用本文设计的方法,进行航天器热平衡温度估计。在此过程中,先建立航天器热平衡温度数学模型,引进灰色马尔可夫链,建立温度状态转移函数。在此基础上,通过对航天器热平衡温度估计值的校正,实现对航天器热平衡温度的估计。

为确保试验结果具有一定的可比性,引进基于STAR-CCM+的热平衡温度估计方法与基于三维/一维强耦合模型的热平衡温度估计方法,将其作为传统方法1与传统方法2。使用本文方法及传统方法1、传统方法2对航天器热平衡温度进行估计,在此过程中调用计算机后台记录数据,描述航天器热平衡温度估计值的训练过程,如图6所示。

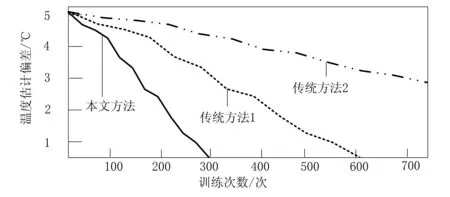
图6 3种方法对航天器热平衡温度估计值的训练过程

从图6可以看出,本文方法在训练300次后,航天器热平衡温度估计值偏差趋近于0。传统方法1在训练600次后,航天器热平衡温度估计值偏差趋近于0。传统方法2在训练超过700次后,航天器热平衡温度估计值偏差仍相对较大。上述试验初步证明,本文方法可以在较少的训练条件下实现对航天器热平衡温度的高精度估计。

完成上述试验后,现场进行航天器热平衡温度值的测量,将测量结果作为参照值。在人工测量温度的过程中,使用本文方法与两种传统方法对航天器热平衡温度进行估计,对比航天器热平衡温度估计值与人工测量值,将其作为评价本文设计方法可靠性的关键指标。统计结果如图7所示。

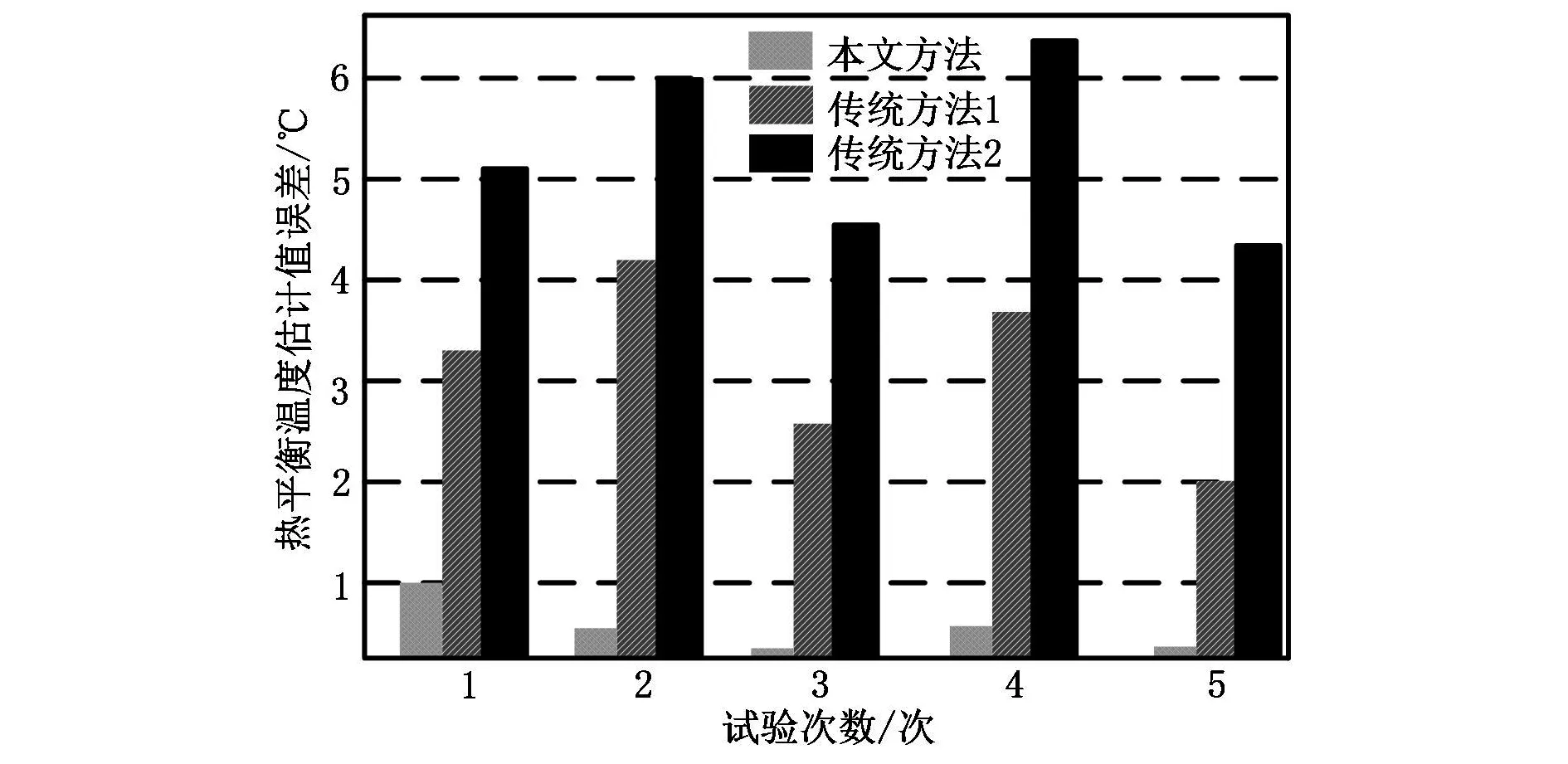
图7 航天器热平衡温度估计值误差统计结果

从图7可以看出,3种方法中,只有本文设计的方法可以实现将航天器热平衡温度估计值误差控制在1℃范围内,而传统方法1与传统方法2的航天器热平衡温度估计值误差均相对较大。

因此,在完成上述试验后,可以得到如下结论:相较于传统方法,本文设计的基于灰色马尔可夫链的航天器热平衡温度估计方法在实际应用中的效果良好。该方法不仅可以在较少的训练条件下实现对航天器热平衡温度的高精度估计,还可以有效降低航天器热平衡温度估计值误差。

6 结束语

热平衡温度估计试验主要用于检测航天器热综合设计的合理性、修正航天器热分析模型,是空间环境模拟试验工作中的一项系统级别试验,也是验证航天器综合设计水平的关键指标之一。此项工作具有时间长、工作量与任务量大、成本高、投入人力资源多等特点。随着航空航天事业的快速发展,航天器的建设规模越来越大,多任务模式验证工作越来越复杂。与此同时,航天器热平衡温度试验与温度估计的误差控制难度也日益增加。为了解决此方面的问题,本文引进灰色马尔可夫链,通过建立航天器热平衡温度数学模型、建立温度状态转移函数、进行航天器热平衡温度估计值校正,设计了一种针对航天器热平衡温度的全新估计方法。通过对比测试,证明该方法可以在较少的训练条件下实现对航天器热平衡温度的高精度估计,从而有效降低航天器热平衡温度估计值误差。