生活教育理念下小学数学启智课堂的应用研究

程垭君 彭建国

【摘要】生活教育是陶行知教育思想的主线和重要基石，在此基础上我校开发了启智课堂，非常注重培养学生的数学思维能力.启智课堂的教学理念不仅决定了学生在后期学习过程中是否能养成良好的学习习惯，而且对学生数学学习的长期稳定发展有着重要的意义.文章从四个方面展开探究小学启智课堂教学中培养学生数学思维能力的方法，从而达到在小学阶段培养数学思维能力，用数学思维实现生活教育的目的.

【关键词】生活教育；启智课堂；数学思维

前 言

虽然新课程改革已经进行了相当长一段时间，但很多一线教师在课堂教学中还是采用教师讲述为主的教学方式，学生只是被动接受知识，导致学生描述不出知识的思维过程，所以很多学生到了中高年级之后，数学成绩会一落千丈.由此可见，数学思维从低年级的数学课堂就要开始训练了.同时，数学教师考查学生学习成果也多以试题的形式，只注重结果是否正确，很少注重学生思维的发展，这也使得学生不太愿意主动、自主的思考.自新课标修订之后，教师则更加注重培养学生核心素养，核心素养具体表现为“三会”，“三会”中最重要的是用数学思维思考现实世界，可见培养学生的数学思维已经迫在眉睫.

一、基本概念

（一）生活教育

生活教育的理论是陶行知教育思想的主线和重要基石.什么是“生活教育”呢？陶行知指出：“生活教育是生活所原有，生活所自营，生活所必需的教育.教育的根本意义是生活之变化.生活无时不变，即生活无时不含有教育的意义.”

（二）启智课堂

启智课堂是一种秉承以生为本、能力为重、启智为真的理念，以培养身心健康、品行优良、善于学习、善于生活、善于创新的“健行少年”为目标的课堂教学模式.启智课堂的主要特征是：以“先学后教，以学定教”为原则，以“三单”即预学单、启学单、温学单为驱动方式，以“五学”即自学、互学、导学、练学、问学为主要板块，以“四重二让一强”即重自学、重探究、重交流、重反思、让时间、让表达、强主体为主要特征的课堂文化.

（三）数学思维

思维是指人的大脑对于外界客观事物的非直接的、概括性的认识过程.数学思维是用数学思考问题和解决问题的思维活动方式，数学思维是抽象的、统一的、严谨的.它分为动作思维、形象思维、抽象思维，具有深刻性、灵活性、独创性等品质.

二、小学生数学思维的特点

小学生的数学思维还处在初级发展阶段，由于学习者的年龄小、小学数学知识结构不完善等因素使得数学思维能力的发展有一定的局限性，但也具有可培养的特殊性.

（一）思维的形象性

小学生数学思维以具体形象思维为主，因此，教师所进行的所有的知识教学都不应离开“具体事物”的导入，不离开学生的直接经验，以这些具体事物、具体情境来进行教学，让学生理解书本上的抽象知识.

（二）思维的灵活性

小学生的思维具有很大的灵活性，然而如何促使他们发挥想象力，就要求教师进行合理的引导，这样学生才能合理地进行发散、联想甚至创造出解决问题的方法.

（三）思维的自觉性

小学生思维能力是需要启发并诱导的，他们并不会自觉地去思考，尤其是需要教师进行引导.如果教师只一味采取满堂灌的教学方法，使学生养成了当“听众”的习惯，那么学生就更不会产生自主思考了.

（四）思维的情境性

小学生的注意力发展不够集中，专注力也不够，同时其情绪也很容易受外界影响，这就影响了他们的思维能力发展.所以教师在课堂上要营造出良好积极向上的学习氛围，促进学生思维的发展.

三、生活教育理念下小学数学启智课堂的应用研究

（一）活泼有趣的具体学生生活导入，激起学生数学思维

如，在教学苏教版二年级上册“认识多边形”时，教师开篇设计了一个视频动画展示了我国古代建筑上的窗格图案，一边介绍其历史文化，一边出示相关图片，学生们都感到无比的兴奋，在学生初步地感知这些窗格图案之后，顺势提出问题：这里面有你熟悉的图形吗？学生此时的大脑立刻会想出自己学过的图形，以及自己在生活中见过的图形.这一教学环节不仅激发了学生的学习兴趣，也激起了学生的数学思维能力，让学生大脑瞬间就活跃了起来，那么课堂上良好的气氛也就营造了起来.

再比如苏教版一年级上册“认识11～20各数”，教师用教具小棒，让学生自己从1数到10，顺势提出：“这里有几根小棒啊？”这其实是一个相对来说较为抽象的问题，可是学生自己动手数了，自然就明白是10根小棒代表的意义，用具体形象的事物来开篇，学生不仅觉得有趣，而且思维也会更活跃.

再比如在教学“用字母表示数”时，教师设计一只只青蛙蹦蹦跳跳地出现在课件上，学生思维顿时活跃、兴趣浓厚，教师顺势提出：1只青蛙1张嘴，2只眼睛4条腿，那2只青蛙（ ）张嘴，（ ）只眼睛（ ）条腿，……学生觉得非常有趣，然后跟着教师一起思考，一起探究.

其实这些案例都告诉我们，小学生的思维都是以具体形象思维为主，教师用具体形象的情境来引入课题，不仅可以激发学生的学习兴趣，还能调动学生已有的经验知识，使其积极地参与课堂教学.当然这就要求教师了解本班学生的具体情况，设计合理合情的情境，这样才能适合学生的思维发展.

（二）新知探讨研究中结合学生生活，使学生数学思维之花开满课堂

一节课的重点当然就是新知的学习，新知的学习到底采用何种形式才能达到教学目的，这就要求教师设计合理的过程，学生参与度高，对新知的理解才会更加深刻，学生的思维发展才会更加深刻.

在教学“认识多边形”时，教师设计了以下几个活动环节：活动一是描边，在学生找出熟悉的三角形之后，教师顺势提出让学生动手描边，学生只有自己动手描过之后，才能感受封闭的三条边连接起来就是三角形，才能更加深刻地理解三角形的定义，在头脑中对三角形又有了新的认识，这就是思维的隐性过程.活动二是找四边形，在教师提供的图形库中指出四边形，再描一描四边形，这个过程是本节课的重点.教师可要求学生小组合作，小组长要合理安排组员指出四边形，然后组内判断是否找正确，再描一描.在这个过程中，教师要注重四个问题：组内人员是否都在学？组内人员都在向谁学？组内人员如何学？组内人員学得好吗？这一系列问题都是培养学生思维能力的重点.组内人员是否都在学：每个学生找到一个四边形，要指给全组人员看；组内人员都在向谁学：每个组员都可以举手发言表达自己的观点，当然这就要求小组长有一定的组织能力；组内人员如何学：这是一个隐性的过程，学生在找四边形、指四边形的过程中，其实就已经对四边形有了自己的认识，这个时候就需要一个比较权威的小组长来引领大家描四边形和描述什么样的图形是四边形，从而培养学生的思维能力；组内人员学得好吗：组内人员是否都能找到正确四边形并正确描边，能否说出来什么样的图形是四边形.活动三是找人描五边形和六边形.这个过程，学生在了解四边形的基础上是可以自主探究完成的.活动四是在钉子板上围多边形，这个过程能够让学生在动手操作的过程中更加深刻地理解多边形的认识，明确有几条边就是几边形，使学生思维发展更加深刻.活动五是魔术展示，教师通过展示剪多边形，把四边形变成两个不同的多边形吸引学生的注意力，学生会非常积极参与，大脑不停地转动着，运用课堂所学的知识“变”出不同的多边形.很多学生在成功剪出多边形之后都高兴得手舞足蹈，课堂气氛达到了高潮.

再比如“认识11～20各数”中教师设计了以下几个环节：环节一是“认识一个十”，学生自主动手把10根小棒捆成一捆，其实有些学生捆小棒的能力是很欠缺的，可是他们依然兴致勃勃地自己动手把小棒用皮筋扎起来.这个过程中学生思维发生了量变，学生体会了捆的过程，明白了这一捆就是10根小棒，明白了10个一和1个十其实都是10根小棒，只是形式不同，计数方式不同而已，从而初步感知出计数单位的含义.环节二是“摆十几”，教师先明确摆12根，并提出要求：如何能一眼就能看出是12根小棒，面对具体问题学生就会积极思考，然后在此基础上摆其他的十几，学生在自主摆小棒的过程中思维再次发生了量变.环节三是“认识20”，先让学生摆好19根小棒，然后再添上1根，接着让学生想办法如何一眼就能看出是20根小棒，引导学生想到捆小棒，这样学生再一次体会满十可以捆为一捆，学生的思维发展有了质的飞跃.

新课标中培养学生的数学思维包括了一个重要的能力就是运算能力，比如在教学“三位数加三位数的笔算”时，教师设计了两个大环节，环节一是让学生实物感知“满十进一”，先让学生小组摆小棒计算142+86，并在小组内说一说摆法和发现.学生积极参与，积极思考，小组内相互交流，初步感知体会十位上满十可向百位进一的规律.为培养学生的具体形象思维，教师可让学生再用计数器拨一拨，边拨边说.在这个过程中，学生根据小棒的经验进一步感受十位上满十向百位进一，进一步抽象计算过程，提升了学生的思维能力；环节二是根据摆小棒和拨计数器的经验，来列竖式计算，并让学生根據竖式说计算过程，学生在这个过程中体会了从具象计算过程到抽象计算过程，理解算理，丰富算法，培养了学生抽象思维能力.

教授新知是发展学生数学思维的重要环节，《义务教育数学课程标准（2022年版）》尤为重视学生体验活动，让学生在参与、体验的过程中来学习新知，这和启智课堂的“先学后教、以学定教”相互呼应，只有学生先学了，教师才知道学生学习的现状，再根据学情确定教法.启智课堂更加注重在新知过程中强调学生自学互学，在自学互学的过程中激发学生运用生活经验解决新知遇到的问题，让学生数学思维之花开满新知探索的课堂.

（三）交流分享成果，形成学生生活具体经验，使学生数学思维之花结出果实

在课堂教学上，学生通过分享交流，把自己的想法、自己的所得说出来.这不仅使学生对知识学习更加清晰，也使学生的思维更加深刻.

在“认识多边形”一课中，教师设计在每个活动环节之后都要进行集体交流，第一个环节是学生描自己熟悉的三角形的边，学生在展台上分享自己作品时，边指边说.几个学生交流展示之后，教师顺势提出：这些图形大小、形状都不一样，为什么它们都是三角形呢？从而让学生明确有封闭三条边的图形是三角形.在这个环节中，学生对多边形有了一个初步的感知.第二个环节中，学生在进行充分的组内交流后，再进行集中交流，学生在展台上展示自己找的、描的四边形.几个学生交流之后，教师顺势提出：这些图形大小、形状都不一样，为什么它们都是四边形呢？使学生进一步明确：只要是像这样有4条边的图形就是四边形，使学生思维更加理性，更加成熟深刻.从而为下一个环节认识五边形和六边形做好准备，这样第三个环节进行起来也会更加顺畅，学生的语言表达就更加准确.在第四个环节“围钉子板”中教师更是深化了学生对多边形的认识，促使学生思维能力进一步提高，能够在表述中明晰自己的思维，迁移并运用了本节课知识，理解不同的多边形，思维更加深刻.这些环节的设计使数学教育更加有力地培养了学生思维发展.

在“认识11～20各数”课堂教学中，学生在第一个环节中，通过捆一捆小棒之后交流10个一和1个十有什么关系.学生开始回想自己刚才摆的10个一和自己捆的1个十，就会发现并得出：10个一就是1个十，让学生的思维从具体形象到初步抽象，实现了一个质的提升.在第二个环节“摆十几”中，学生们会产生不同的摆法，教师要善于利用学生的资源，生成新的教学资源，让学生在对比中，自主探究发现出：一捆加两根就是12根，这对后面摆其他的十几意义非凡，学生再摆其他十几的数，就会从中领会出其中的意义，这样课堂的趣味性更浓厚，学生参与度也就更高了.第三个环节“认识20”中，教师可提出：“为什么会有两捆呢？”的问题.另外一捆哪里来的呢？学生会在交流中更加深刻地理解满十捆一捆，从而使思维更加敏锐.

从这两个案例可以看出，学生在课堂上交流的重要性，它不仅可以使学生知识学习更加系统，还使学生数学思维更加敏锐深刻，这也是数学教育需要达到的目的.

（四）总结概括全课，使学生数学思维之果实更加丰硕

数学课堂上如果只有教学过程没有总结是不完整的、缺乏深度的，数学课堂的总结是为了使学生知识学习更加系统，也使学生思维发展更加完整且具有体系.

在“认识多边形”课堂中，每一个环节的最后，教师都要进行小结.比如，第一个环节教师就会小结出：不管图形的形状、大小怎样，只要是像这样有3条边的图形，它就是三角形，从而使学生对三角形有了进一步的认识，对边的数量和几边形有了初步感知.第二个环节之后教师又会小结出：是的，只要是像这样有4条边的图形就都是四边形，跟它们的形状、大小是没有关系的.学生进一步体会了边的数量和几边形之间的关系，从而在理解五边形、六边形甚至其他边形的图形时，学生也会顺势迁移所学知识.所以最后在五边形、六边形认识之后小结出：三角形、四边形、五边形、六边形等，它们有一个共同的名字叫多边形，这就是我们今天学习的认识多边形.进而深化了本节课的知识，也对本节课的知识进行了概括.在课堂的最后要进行全课总结，让学生自行谈收获，最后教师总结本节课所学知识，使学生串连起整堂课的知识，思维也有了连续性的发展.

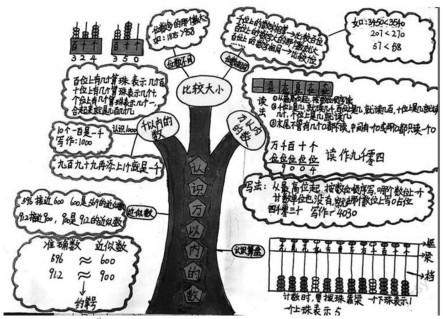
总结概括是为了让学生对整节课知识或者整个单元知识有个整体认识，这个时候思维导图起到了很大的作用.在教学中，每一个单元结束，教师可以让学生先小组讨论这个单元学习了哪些知识，列提纲整理一下，然后将知识进行丰富形成一幅幅思维导图.这个过程中极大地发展了学生思维能力.比如“认识万以内的数”的思维导图：

总之，培养小学生数学思维不仅是小学数学课堂教学的基本任务，也是整个数学教育的持续任务，教师要根据小学生具体生活情境和思维特点以及小学数学课堂教学实际情况，利用启智课堂教学设计，在课堂上放飞学生思维，找出适合所有学生发展的数学课堂设计，让数学课堂开满思维之花，使数学思维指导服务于学生的整个学习生活.

【参考文献】

[1]何小亚.数学学与教的心理学[M].广州：华南理工大学出版社，2011.

[2]杨健.放飞思维，让小学生在数学学习之路上走得更远———谈小学数学教育[J].才智，2019（18）：141.

[3]周齐才.有心栽柳柳成林———数学思维教学例谈[J].科学咨询（教育科研），2019（11）：144.

[4]刘艳明.小学生数学思维特点的研究[J].理论界，2007（09）：128-129.

[5]马渊.谈小学数学教学与学生思维能力的培养[J].才智，2020（16）：31.

[6]陶行知.陶行知文集[M].南京：江苏教育出版社，2008.