多角度理解 构建概念全过程
马希纯
【摘要】概念教学是数学教学中的重要内容.教师通过概念教学,可以使学生对数学知识有更加准确的了解.文章以“倒数”教学为例,就如何通过多角度的理解帮助学生进行全过程的概念构建进行了探讨,希望可以为概念教学提供借鉴.
【关键词】概念;数学;全过程
教学内容
义务教育教科书《数学》五年级下册第31面“倒数”.
课前思考
1.经历概念发现的过程,概念建构要经历感知—表象—抽象—运用四个阶段.教材中分别通过“认识倒数”“借助面积为1的长方形,认识它的长和宽互为倒数”“求倒数”“理解0为什么没有倒数”这四个环节讲授“倒数”.在这个过程中,学生会产生新问题.而这四个环节的呈现方式是教师值得关注的问题.概念认识的全过程能够驱动学生主动进行质疑与探究,主动地构想学习目标与策略,从而更加充分地经历概念建构的过程,更加深刻扎实地理解概念.
2.“倒数”是一节概念课,倒数的表象为分子、分母互相颠倒,本质为乘积为1的两个数互为倒数.理解倒数的内涵与外延,沟通内涵与外延之间的联系是本节课的重点目标之一.
教材借助几何直观图探究长方形的长、宽与面积三个量之间的关系,即面积为1的长方形,其长与宽互为倒数,从而突出倒数的本质为乘积为1的两个数,进而引导学生透过它的表面特征“分子、分母相互颠倒”,关注倒数的本质.乘法在本质上是一类特殊的加法.一般地,规定乘法运算a×b表示a个b相加.学生对乘法的理解除了定义中相同加数的和之外,还有其他的一些重要模型或现实背景,主要有五个方面:求几个几是多少,求一个数的几倍是多少,数量关系,长方形的面积以及搭配问题(如图1).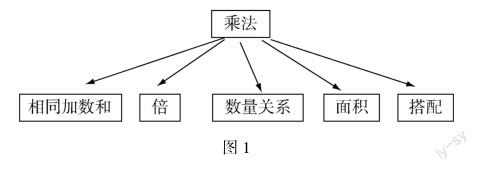
教材中引入长方体的面积模型旨在利用乘除颠倒的原则突出倒数的核心,认识倒数的本质,淡化倒数的表面特征.
3.在课前小测中,以海港湾学校五年级一班、二班共83名学生为调查对象,调查数据反馈27.71%的学生对倒数没有了解,72.29%的学生认为倒数是分子与分母互换的两个分数.基于以上考虑,我将本节课的教学目标定为:
1.经历倒数的发现过程,多角度理解倒数的意义.
2.会求一个数的倒数,并能解决问题.
教学重难点
重点:多角度理解倒数的意义.
难点:理解倒数的本质,淡化倒数的表面特征.
以问题为抓手,以概念建构为目标,我设计了以下教学过程.
教学过程
一、填写算式,发现关系【感知、表象】
1.课前梳理
师:关于倒数的知识我们已经做了课前小调查,同学们主要想知道什么是倒数和学习倒数有什么用.
问题1:什么是倒数?
生1:倒数是从后往前数的数,如100,99,98……
生5:倒数的乘积是1.
问题2:学习倒数有什么用?
师:这节课我们就一起来探究这两个问题,相信通过今天的学习你们对倒数会有更深的认识.
2.尝试探究
生1:都是两个数相乘的乘法算式.
生2:两数相乘,乘积为1.
生3:两个乘数的分子、分母互相颠倒.
3.初次释疑.
师:像这样的,乘积为1的两个数互为倒数.
【设计意图:课前引导学生针对“倒数”提出自己想知道的问题,引发学生强烈的好奇心,使学生进行主动提问、主动思考、主动探究.教师呈现算式,要求学生直接计算并观察,对学生多样化的表达进行放大处理.】
二、观察表达,揭示关系【具象、抽象】
算一算,借助长方形的面积来进一步认识倒数.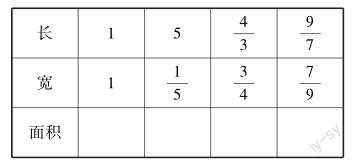
提问:计算出长方形的面积,说说你发现了什么?
生1:面积都为1.
生2:长方形的长和宽相乘结果为1.
生3:互为倒数的两个数分别作为长方形的长和宽,长方形的面积是1.
总结:长和宽互为倒数,长方形的面积为1.
【设计意图:乘法运用在生活中一个重要模型为长方形的面积模型,利用长方形的面积模型突出乘积为1的两个数互为倒数,淡化倒數的表面特征.】
三、对比分类,揭示意义
1.提问:你能否根据长方形的长、宽、面积三个量之间的关系利用倒数的知识自己创作一份表格?
2.学生作品展示
【设计意图:在该环节中,教师要注意寻找乘积非1的错例,1×1=1的作品、小数乘整数的作品、小数乘分数的作品进行辨析与讨论,从而突出倒数的本质,淡化倒数的表面特征,同时引导学生讨论1与0的倒数.在一个环节中解决本课的两个重点知识,将碎片化知识系统化.】
3.学生辨析
提问:(1)观察表格,你有什么想说的?
(2)以上六个表格中有什么相同点与不同点?
生1:第六个表格表示两个量相加,倒数是两个数乘积为1,因此第六个表格中0.75与0.25不成倒数.
生2:两个量相乘可以表示底与高相乘,即平行四边形面积.
生3:两个量相乘乘积为1也可以表示單价、数量、总价之间的关系;时间、速度、路程之间的关系;工作时间、工作效率和工作总量之间的关系;平行四边形的面积与底和高之间的关系;乘数、乘数与积之间的关系.
生4:只要满足乘积为1,单价与数量、时间与速度、工作时间与工作效率、底与高中两个因数之间都是互为倒数.
提问:观察所有数据,你有什么发现?
生5:互为倒数的两个数乘积为1,其他运算都不可以.
生6:互为倒数的两个数不仅可以是分数,也可以是小数、整数,只要满足乘积为1就可以.
生7:1×1=1,因此1的倒数为1.
【设计意图:教师引导学生从面积模型、速度与时间、单价与数量等多个乘法意义的角度理解面积模型,突出倒数的内涵即乘积为1的两个数互为倒数,从而淡化学生直观感受它的外部特征“分子、分母互为颠倒”.分类的过程也是细致研读表格的过程,表达分类理由也就是揭示量的变化规律.在分类过程中,教师引导学生关注各个表格间的相同与不同,由学生自主发现其规律从而突出倒数的内涵.教师也通过学生多个作品的展示与辨析,带领学生逐个攻破乘积非1的错例、解决1和0倒数的问题.】
4.总结:前面先给出长方形的长与宽求面积,发现面积都是1.现在已知乘积为1的长方形,求长与宽,我们一起来探究这一顺一逆的过程.【板书】
四、抽象拓展,运用倒数【抽象】
下面四个长方形的面积都是1,请你填一填,并说说你是怎么想的.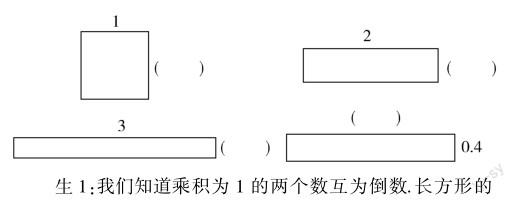

生6:面积是1,那长与宽互为倒数.
提问:长方形的长与宽,有的是整数,有的是分数,有的是小数,它们都有倒数吗?如何求一个数的倒数?
生1:1的倒数是本身.
生2:互为倒数的两个数乘积为1,已知乘积为1,知道其中一个数,能求出这个数的倒数.
生3:求一个小数的倒数,可以用1除以这个小数得到小数的倒数,也可以先把小数换成分数,再求出倒数.
五、结合实例,反馈拓展【运用】
1.提问:0有倒数吗?说一说你的想法.
预设1:0×0=0,互为倒数的两个数乘积为1,不符合.
预设2:0×1=0,改为除法算式1÷0无意义,0不可以做除数.
2.学习倒数的作用
提问:在课前,很多学生也提出学习倒数有什么用,通过这节课的学习你发现倒数有什么作用吗?
生1:用倒数知识可以求面积为1的长方形的长与宽.
生2:用倒数的知识求出一个乘积为1的乘法算式中的乘数.
3.游戏环节———找互为倒数的好朋友.
师:老师在开学前给每个学生准备了一张爱心卡,今天我们利用手中的爱心卡来玩一个倒数的游戏吧.
活动要求:每个成员拿着一个数,去找互为倒数的两个数,组成好朋友,并向对方说明能够成为好朋友的原因.

【设计意图:通过游戏的形式巩固倒数的内涵与外延,呈现两数相加、相减、相除得数为1的形式,最简分数与非最简分数的形式,小数、分数、整数以及0的形式,在对比中突出倒数概念的内涵,增加学习的趣味性,发展学生团结友爱的精神.】
教学板书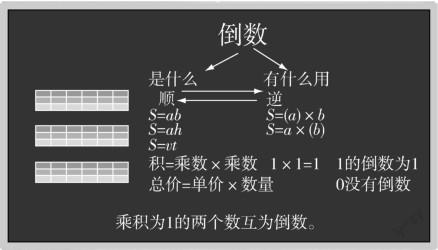
教学总结
1.基于学生知识构建课堂
由于学生课前所接触的知识不同,因此不同学生对倒数有不同的理解,教师基于学情利用课前小测提前对学生进行摸底调查,发现学生对倒数的理解大部分停留在分数的分子分母互相颠倒的层面上,因此教师将本节课的教学重点与难点确定为多角度构建概念,淡化倒数的表面特征,从多角度理解倒数的本质,即乘积为1的两个数互为倒数.
2.深度与宽度相结合
倒数的表面特征是“分子、分母颠倒”,教师借助不同的乘法模型引导学生感知乘积为1的两个量互为倒数.深度挖掘倒数的本质含义与多角度构建概念的全过程.同时,教师在乘法的意义这个大背景下,梳理乘法现实意义与背景模型,丰富感知材料,提供不同角度的支撑依据,让规律的验证更加坚实与可靠.
【参考文献】
[1]吴正宪,刘劲岑,刘克臣.小学数学教学基本概念解读[M].北京:教育科学出版社,2014.
[2]王永春.小学数学核心素养教学论[M].上海:华东师范大学出版社,2019.
[3]龙月琴.小学数学概念深度学习的“五化”策略[J].福建基础教育研究,2021(12):85-87.

