巧用有关函数对称性和周期性的结论解题

闫一君

对称性和周期性是函数的的重要性质，这两种性质是解答函数问题的重要工具.对于一些较为复杂的函数问题，有时需同时运用对称性和周期性求解.若一个函数同时具有对称性和周期性，那么该函数就比较特殊，且具有一些特殊的性质，我们可根据其图象和解析式得出很多相关的结论.

结论1.若f（x）=f（2a-x）或f（a-x）=f（a+x），则函数f（x）的图象必然关于x=a对称.反过来，若函数f（x）的图象关于x=a对称，则f（x）=f（2a-x）或f（a-x）=f（a+x）.

证明：如图1，曲线f（x）关于直线x=a对称，在曲线f（x）上取两点A，B关于直线x=a对称，

则点A，B的纵坐标相等，

横坐标关于点a对称，

设点A的横坐标为x，

则点B的横坐标是2a-x，

可得x的函数值f（x）和2a-x的函数值f（2a-x）相等，即f（x）=f（2a-x）.

如图2，设点A的横坐标为a-x，

则点B的横坐标为a+x，

此时f（a-x）=f（a+x），因此f（a-x）=f（a+x）.

根据结论1，我们可以建立函数解析式、图象、函数对称轴之间的联系，即根据其对称轴可求得函数图象上对称点的坐标，明确对称点的位置，求得函数的解析式.

结论2.若f（x）=-f（2b-x）或f（b-x）=-f（b+x），则f（x）的图象关于点（b，0）中心对称.反过来，若f（x）的图象关于点（b，0）中心对称，则f（x）=-f（2b-x）或f（b-x）=-f（b+x）.

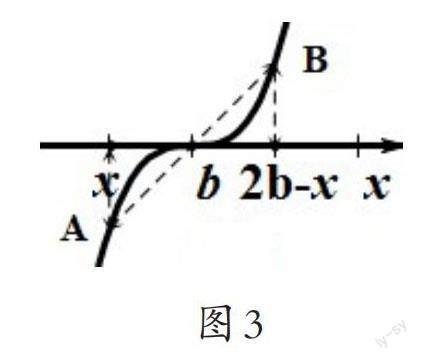
证明：如图3，作一条曲线关于点（b，0）对称，

在曲线上取两点A，B关于点（b，0）对称，

则点A，B的纵坐标互为相反数，

横坐标也互为相反数.

设点A的横坐标为x，

则点B的横坐标为2b-x，则f（x）=-f（2b-x）.

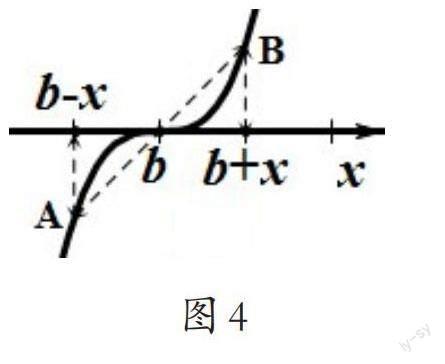
如图4，设点A的横坐标为b-x，

则点B的横坐标为b+x，

则f（b-x）=-f（b+x）.

由结论2，我们可以根据函数的对称性，求得函数图象上对称点的坐标及其关系，明确对称点的位置.

结论3.若f（x+2a）=f（x）或f（x+a）=-f（x），则函数f（x）的周期为2a.

证明：根据函数周期的定义，可知函数f（x）满足f（x+2a）=f（x），则函数的周期是2a.

如图5，正弦函数y=sinx周期是2π，当x=π/6时，sinx=-sin（x+π）；当x取别的值时，sinx=-sin（x+π）仍然成立.这就是说，一个角加上π后，函数值互为相反数，依次类推，这个角加上2π后，两函数的值相等，即sinx=sin（x+2π），那么函數的周期是2π.

需要注意是，若函数f（x）周期是2a（a≠0）时，f（x+2a）=f（x）一定成立，但f（x+a）=-f（x）不一定成立.例题：已知函数y=f（x）的定义域是R，f（x+1）是奇函数，f（x+5）=f（x-3），当x∈[1，5]时，f（x）=log2（x+1），则f（2023）=_____.

解：因为f（x+1）是奇函数，

所以f（-x+1）=-f（x+1），

由于（）

-x+1+（x+1）=2，

所以f（x）=-f（2-x），

即函数f（x）关于点（1，0）对称.

由于f（x+5）=f（x-3），

所以f（x+5-5）=f（x-3-5），

即f（x）=f（x-8），

则函数f（x）的周期是8.

因为2023=8×252+7，

所以f（2023）=f（7）=f（-1），

而函数的图象关于点（1，0）对称，

则f（-1）=-f（3），所以f（2023）=-f（3）.

因为当x∈[1，5]时，f（x）=log2（x+1），

得f（3）=log2（3+1）=2，

所以f（2023）=-2.

因为f（x+1）是奇函数，所以根据奇函数的定义，将函数式进行转换，得到f（x）=-f（2-x），根据结论2可知函数f（x）的图象关于点（1，0）对称.而由f（x）=f（x-8），可知函数的周期是8，即可根据函数的周期性求得问题的答案.

在解答与函数周期性、对称性有关的问题时，要明确自变量的意义，各个变量与自变量之间的关系，从而抓住问题的本质，据此建立关系式.必要时可将数形结合起来，借助图形来明确函数图象的变化情况，以确定函数的对称性和周期性，顺利求得问题的答案.

（作者单位：陕西省神木市职业技术教育中心）