基于主成分-聚类分析法的31个省市经济发展水平的综合评价

何远霞　王兰　焦登丹

［摘 要］文章主要以我国31个省、自治区和直辖市的经济发展水平为研究对象，选取能反映经济发展水平的18个经济指标，运用主成分分析法（Principal Component Analysis，PCA）和系统聚类分析法，对31个省市的经济发展水平进行综合评价。

［关键词］主成分分析；系统聚类法；经济发展水平；综合评价

doi：10.3969/j.issn.1673 - 0194.2023.14.058

［中图分类号］F124［文献标识码］A［文章编号］1673-0194（2023）14-0177-03

0     引 言

我国部分地区因地理环境及气候条件等因素的制约，发展速度较慢，导致我国整体经济发展受到影响。此外，研究发现，我国各省市间经济发展存在严重的不平衡现象。研究各省市间的经济发展情况，对促进各省市更快更好地发展和充分发挥城市在经济社会生活中的主导作用都具有重要意义。

1     数据来源和指标选取

本文数据源于《2022中国统计年鉴》，由Matlab软件完成数据分析。为更加全面地评价2021年我国31个省、自治区和直辖市（以下简称31个省市）的经济发展状况，本文结合各省市经济发展实际情况和数据的科学性、可得性及可操作性等原则，选取能够反映我国31个省市经济发展水平的18个指标：人均国内生产总值（Gross Domestic Product，GDP）（元）、地方一般公共预算收入（亿元）、社会消费品零售总额（亿元）、固定资产投资（不含农户）同比增长率（%）、地区生产总值（亿元）、在岗职工人均工资额（元）、房地产开发投资额（亿元）、地方财政预算支出（亿元）、城乡居民年底储蓄余额（亿元）、客运总量（万人）、貨运总量（万吨）、货物进出口总额（亿元）、人均拥有公共图书馆藏量（册/人）、公共图书馆电子阅览室终端数（台）、普通高等学校数（所）、每十万人口高等学校平均在校生数（人）、人均公园绿地面积（平方米/人）、农林牧渔业总产值（亿元）。将18个指标变量分别表示为X1、X2、X3、X4、X5、X6、X7、X8、X9、X10、X12、X13、X14、X15、X16、X17、X18。

2     基于主成分-系统聚类分析法的31个省市经济发展水平综合分析过程

2.1   选择分析方法——主成分分析

2.1.1   主成分分析方法简介

主成分分析的基本思想是将有一定相关性的多个原变量重新组合成少数几个不相关的综合变量来代替原变量，并反映出原变量的大部分信息［1］。假设某实际问题中有n个样品，对每个样品观测p个指标，分别用X1，X2，…，XP表示，按各个主成分的累计贡献率提取p个主成分（F1，F2，…，Fp）的PCA信息转移方程如下：

（1）

式（1）中aij（i=1，2，…，p；j=1，2，…，p）为第j主成分Fj和第i个原变量Xi的线性相关系数。

一般情况下，当前m个主成分的累积贡献率达到85%时［2］，就选取m（m＜p）个主成分来重新表示p维随机向量X，也实现了降维。

2.1.2   PCA模型的适宜性检验

本文使用KMO检验统计量和Bartlett球形检验方法来检验变量间是否存在相关性，当KMO值接近1，Bartlett球形检验的P值小于或等于0.01时，适合作主成分分析。由表1可知，KMO值0.775＞0.6，且Bartlett球形检验P值接近于0，表明所选指标数据可以作主成分分析。

2.1.3   主成分提取

本文由Matlab软件计算得出特征值、贡献率及累计贡献率，具体如表2所示。

由表2可知，当主成分为3个时，累积贡献率为83.186％，能解释原始变量所包含的信息，因此，本文提取前3个主成分，记作：第一主成分F1、第二主成分F2和第三主成分F3。

由式（1）和Matlab计算得到的3个主成分表达式如下：

F1=0.129X1+0.293X2+0.308X3+0.079X4+0.310X5

+0.024X6+0.304X7+0.309X8+0.302X9+0.264X10+

0.260X11+0.261X12+0.034X13+0.283X14+0.283X15+

0.053X16+0.060X17+0.241X18（2）

F2=0.449X1+0.158X2+0.015X3+0.040X4+0.026X5

+0.490X6+0.018X7+0.014X8+0.028X9+0.063X10+

0.149X11+0.233X12+0.479X13+0.165X14+0.136X15+

0.185X16+0.181X17+0.328X18（3）

F3=0.075X1+0.119X2+0.050X3+0.582X4+0.072X5

+0.160X6+0.099X7+0.049X8+0.010X9+0.112X10+

0.003X11+1851X12+0.057X13+0.049X14+0.206X15+

0.640X16+0.283X17+0.109X18（4）

由式（2）、式（3）、式（4）可知，第一主成分F1所有变量的系数都大于0，反映了综合经济发展水平情况，F1值可粗略反映整体经济发展水平的高低；第二主成分F2只有变量X1、X6和X13的系数较大，剩余变量的系数都比较小或小于0，因此F2反映了在岗职工工资和图书投入经济情况；第三主成分F3只有变量X4和X16的系数较大，其他变量的系数比较小或小于0，因此F3反映了固定资产投资或高等教育投资经济情况。

F1、F2和F3分别从不同方面反映了各省市的经济发展水平，为更好利用F1、F2和F3的信息，本文将它们按贡献率综合如下。

综合主成分表达式如下：

（5）

式（5）中，F数值大小反映了各省市经济发展的综合效果，即F的值越大，经济综合水平越高，反之越低。

2.1.4   主成分得分及综合得分

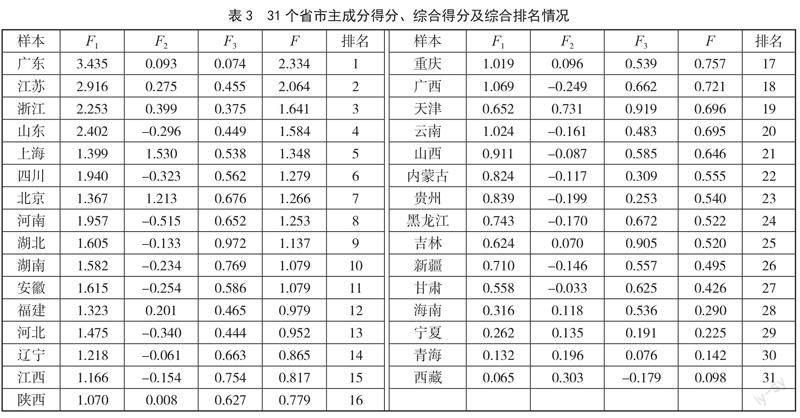
本文由Matlab软件计算出各省市的F1、F2、F3及F的值，并按F值排名，具体如表3所示。

由表3可知，排名前10的省市分别为广东省、江苏省、浙江省、山东省、上海市、四川省、北京市、河南省、湖北省和湖南省，这些省市的工农业发展规模较大、产值较高，且发展水平居全国前列［3］。排名靠后的省份，如海南省，旅游业是海南省的支柱产业，第一、第二产业都不发达，又受近两年特殊情况的影响，旅游产业非常不景气，所以海南省的经济状况不好。对于宁夏回族自治区、青海省和西藏自治区，都是我国西部的省（自治区），人口均不足1 000万人，由于地理环境、气候环境等各方面因素的影响，这些地区的生产力欠发达，所以经济实力比较差。

2.2   系统聚类分析法

2.2.1   系统聚类法介绍

系统聚类法又叫分层聚类法，是目前最常用的聚类分析方法，指利用距离和相似系数把分类对象分成若干类的过程［4］。

本文選用离差平方和法（Ward）来测量类间距离。Ward方法是利用方差分析的思想来推导类间距离，如果分类正确，则同类之间的离差平方和应当较小，而不同类样品之间的离差平方和应当较大［5］。

2.2.2   31个省市经济发展水平的分类

本文选取上述PCA提取的3个主成分F1、F2和F3指标作系统聚类分析，利用Matlab软件得到系统聚类树形图，如图1所示。

基于图1，本文把31个省市的经济发展水平分为5类。第1类是综合水平高的省市，有江苏省、浙江省和广东省。这3个省的各主成分和综合成分的得分都比较高，尤其F1和F值均排名前三。因此，从综合经济发展情况来看，这3个省的经济发展水平远高于其他省份，这与实际相符。第2类是综合水平中高的省市，有北京市和上海市。这两个市的各主成分和综合成分得分较高，但综合成分得分较第1类中的3个省次之，说明北京市和上海市整体综合经济发展水平在31个省市中居于中上水平。第3类是综合水平居中的省份，有河北省、安徽省、山东省、河南省、湖北省、湖南省和四川省。其特点是F1值较高，说明这几个省的综合经济发展比较好，主要原因是这几个省的农业发展相对成熟，居31个省市前列。虽然综合经济发展较好，但F2值均为负值，说明这几个省的在岗职工工资和图书投入等情况不太理想。第4类是综合水平中低的省市，有天津市、山西省、内蒙古、辽宁省、吉林省、黑龙江、福建省、江西省、广西壮族自治区、海南省、重庆市、贵州省、云南省、陕西省、甘肃省以及新疆维吾尔自治区。这几个省（自治区）的F1值次于第3类，F2值与第3类相近。第5类是综合水平低的省市，有西藏自治区、青海省和宁夏回族自治区。这3个省（自治区）的F1、F2以及F3的值都极低，说明这3个省的综合经济发展水平是31个省市中最低的。

3     研究结论

本文主要运用PCA法和系统聚类法对31个省市的18个经济指标进行处理分析，对31个省市的经济发展水平作了综合评价。从PCA法的分析中可知，第一主成分F1的表达式中每个变量系数均为正值，虽然部分系数很小，但整个F1的贡献率达55.81%，说明各省市要想提高经济发展的总体水平，需要考虑每个指标；F2主要反映在岗职工薪资和图书馆馆藏量情况，贡献率为19.589%。一个发达的省市，员工薪资和文化建设也一定发达，所以员工薪酬和文化建设对一个省市经济发展水平的衡量来说是必须考虑因素的；F3反映了固定资产投资或高等教育投资经济情况。由主成分F1、F2和F3的值可知，31个省市之间的经济发展差距是比较大的。

主要参考文献

［1］朱建平.应用多元统计分析［M］.北京：北京大学出版社，2017：119-137．

［2］潘若愚，贺尔蓉.我国沿海钢铁产业基地布局研究［J］.经济研究参考，2011（56）：29-35.

［3］李文军.山东省地级市经济发展水平评价［J］.临沂师范学院学报，2003（6）：77-80.

［4］周品.MATLAB概率与数理统计（最新版）［M］.北京：清华大学出版社，2012：11.

［5］韩文革，于晓春.聚类分析在鹰嘴豆农艺性状分类上的应用［J］.内蒙古农业科技，2006（6）：40-41，45.