高强钢Q960E对接接头残余应力与焊接变形的数值模拟

骆文泽 成慧梅 刘红艳 王义峰 叶延洪 邓德安

1.重庆大学材料科学与工程学院,重庆,400045

2.河钢集团邯钢公司,邯郸,056015

0 引言

在当前努力实现“碳达峰”和“碳中和”目标的背景下,采用低合金高强、超高强钢材替代如汽车、轨道车辆和船舶等运载工具、工程机械及矿山机械中使用的传统碳钢材料,能显著降低结构的自重,进而减少能耗,达到环境友好的目的,并能带来良好的社会效益和经济效益[1-3]。Q960调质钢(屈服强度不低于960 MPa)是我国近年来开发的低合金高强钢,目前已经开始用于实际工程结构的制造。

在钢结构焊接组装过程中,熔化焊接技术由于其成本较低、生产率高以及适应结构设计的灵活性大等优势而被广泛采用。但是,由于电弧热源具备热流密度大且局部集中的特点,在焊接过程中不可避免地会形成非均匀温度场,从而导致焊件中产生高的残余应力和显著的焊接变形[4]。焊接过程中的瞬态拉应力和拉伸焊接残余应力分别是热裂纹和冷裂纹产生的重要诱因,而拉伸残余应力在服役过程中不仅会缩短结构的疲劳寿命和加剧应力腐蚀,甚至会导致结构发生脆性断裂;焊接产生的压缩残余应力在薄板结构中会显著降低结构屈曲强度与稳定性。理论上,焊接导致的残余应力峰值与材料屈服强度成正相关关系,即材料的屈服强度越高,焊后产生的残余应力峰值越大,该峰值可以达到甚至超过材料的常温屈服强度。

国内外学者近年来对Q345、Q390和Q460等强度级别相对较低的钢焊接接头或结构的残余应力与焊接变形已经进行了较为系统和深入的研究[5-10],并获得了较丰富的实验数据和数值模拟结果。上述几种材料本身的碳当量相对较低,焊接热影响区组织中的中温转变相(贝氏体)和低温转变相(马氏体)相对较少,加之所选用焊材形成的熔覆金属含碳量和碳当量一般要低于母材,焊缝组织一般以针状铁素体为主,因此在采用数值模拟方法计算这类钢材焊接接头或结构残余应力和焊接变形时,往往不需要考虑固态相变对焊接残余应力与变形的影响。但是,对于Q960这类屈服强度接近1000 MPa以及碳当量达到0.6%以上的钢材,焊接接头的热影响区会产生马氏体,而固态相变可能会对接头残余应力分布与大小有较为显著的影响。

SUN等[11]采用实验手段和数值模拟方法研究了S960钢的焊接残余应力,重点考察了温度与材料屈服强度对残余应力预测精度的影响。该研究采用的是单道重熔模型,并没有讨论多层多道焊接条件下的残余应力。SCHAUPP等[12]测量了调质状态和热机械控制工艺状态下名义屈服强度为960 MPa钢的单道非熔化极惰性气体保护电弧(tungsten inert gas,TIG)焊重熔接头的焊接残余应力,并讨论了焊接热输入和预热温度对残余应力的分布与大小的影响。但是,在该研究中并没有详细讨论固态相变对残余应力的影响。

实际工程结构中的Q960调质钢厚度往往不小于6 mm,因此大多采用多层多道的焊接工艺来完成焊接,同时基本采用等强匹配的原则来选用焊接填充材料。本研究将以Q960E低合金调质钢多层多道对接接头为研究对象,通过实验测量和模拟计算相结合的方法建立材料的热物理性能和力学性能数据库,以SYSWELD软件为平台,开发考虑“热-组织-应力”多物理场耦合的数值模拟方法分别计算对接接头的温度分布、热影响区的组织体积百分比、残余应力和焊接变形,并通过比较焊接接头残余应力与焊接变形的实验测量结果和数值模拟结果,以验证所开发模型的可靠性。最后基于数值模拟结果,探究固态相变对Q960E对接接头残余应力的影响,并揭示接头热影响区残余应力的形成机理。

1 实验方法

1.1 焊接实验

本研究所用Q960E钢为低合金调质钢,调质处理时,加热至910 ℃保温后进行淬火,回火温度为560 ℃,其供货状态微观组织是回火索氏体,常温屈服强度约为1000 MPa。根据等强匹配原则,本研究选用了ER120S-G焊丝作为填充材料,母材与焊材的化学成分如表1所示。图1所示为焊接试板尺寸与坡口形状,试板尺寸为280 mm×360 mm×10 mm,坡口为单V形坡口,坡口角度为60°,钝边为1 mm。4条焊道的布置情况如图2所示。

图1 对接接的尺寸与坡口形状

图2 焊道布置及热电偶位置

表1 Q960E钢与ER120S-G焊材的化学成分(质量分数)

焊前对被焊工件表面先进行除锈处理。为防止冷裂纹的出现,将工件进行150 ℃的焊前预热。待预热完成后,采用半自动混合气体保护焊(gas metal arc welding,GMAW)进行焊接,保护气为80%Ar+20% CO2的混合气体(均为体积分数),气体体积流量为20 L/min,层间温度控制在150 ℃左右。焊接工艺参数如表2所示。在焊接过程中采用热电偶测量典型位置的温度循环,热电偶位置如图2中A、B、C所示,其中A、B、C位置距离最后一道焊缝的焊趾位置分别为2.5 mm、4.9 mm和7.1 mm。为防止冷裂纹的出现,焊接完成后,在200 ℃温度下进行2 h的后热处理,随后将试板静置72 h。最后,采用X光对焊缝进行探伤。

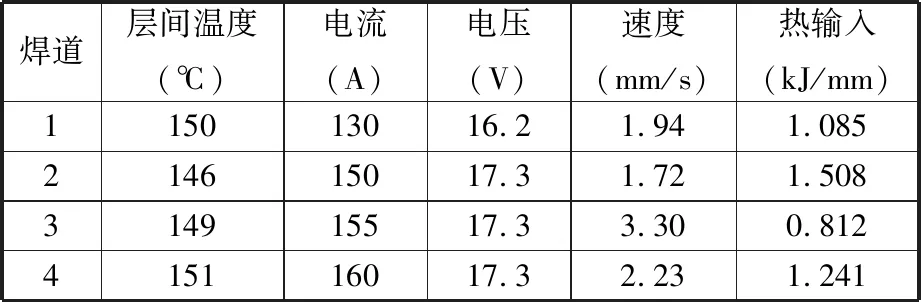
表2 各焊道的焊接参数及热输入

1.2 应力测量方法及位置

焊接完成后,采用小孔法测量接头上表面的焊接残余应力。小孔法测量应力时,需先将应变片贴于待测工件表面,然后采用机械打孔的方法释放待测位置的弹性应变,通过应变仪收集电信号,最后通过理论计算得到残余应力[13]。本研究采用的应变仪型号为HK21A,应变片型号为BE120-2CA-K。应力的测量位置如图3所示,其中,图3a为应力测量区域示意图,图3b为应变片布置示意图。

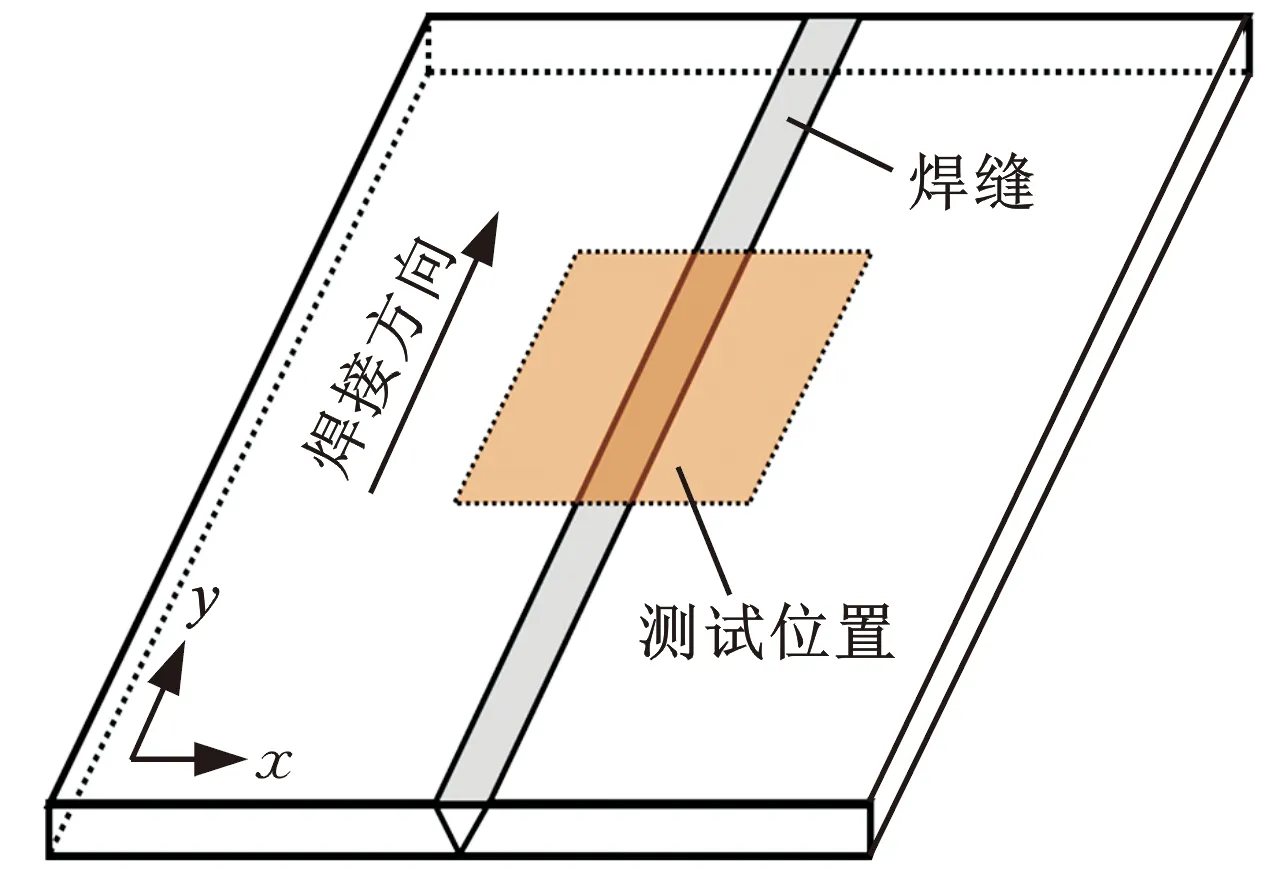
(a)应力测试位置

1.3 焊接变形测量

焊接横向收缩和角变形的测量示意图见图4。图4a所示为横向收缩测量方法,焊接前分别对焊缝两侧进行打孔,左右两侧分别打孔3个,两侧间距为40 mm,单侧孔距为90 mm。然后采用游标卡尺对两侧孔距进行测量,根据焊前和焊后各孔位相应距离的差值就可得到横向收缩的大小。图4b所示为投影法测量角变形,将焊接前后的试样轮廓投影至投影平面,再通过焊前和焊后投影位置差异的测量得到角变形。

(a)横向收缩测量 (b)角变形测量

1.4 组织与硬度测试

待残余应力实验完成后,采用线切割机在中央截面位置取出尺寸为50 mm×10 mm×10 mm的金相样品,并对它进行砂纸打磨、抛光和腐蚀处理。采用蔡司Axio Scope.A1显微镜观察焊缝(fusion zone,FZ)、热影响区(heat-affected zone,HAZ)中粗晶区(coarse grained heat-affected zone,CG)和部分相变区(inter-critical heat-affected zone,IC)以及母材(base metal,BM)的微观组织。

另外,采用HX1000 TM/LCD显微硬度仪沿着图5所示的line 1和line 2两条路径进行硬度测试。硬度测试时,压头的压力值为9.8 N,加载保持时间为15 s。

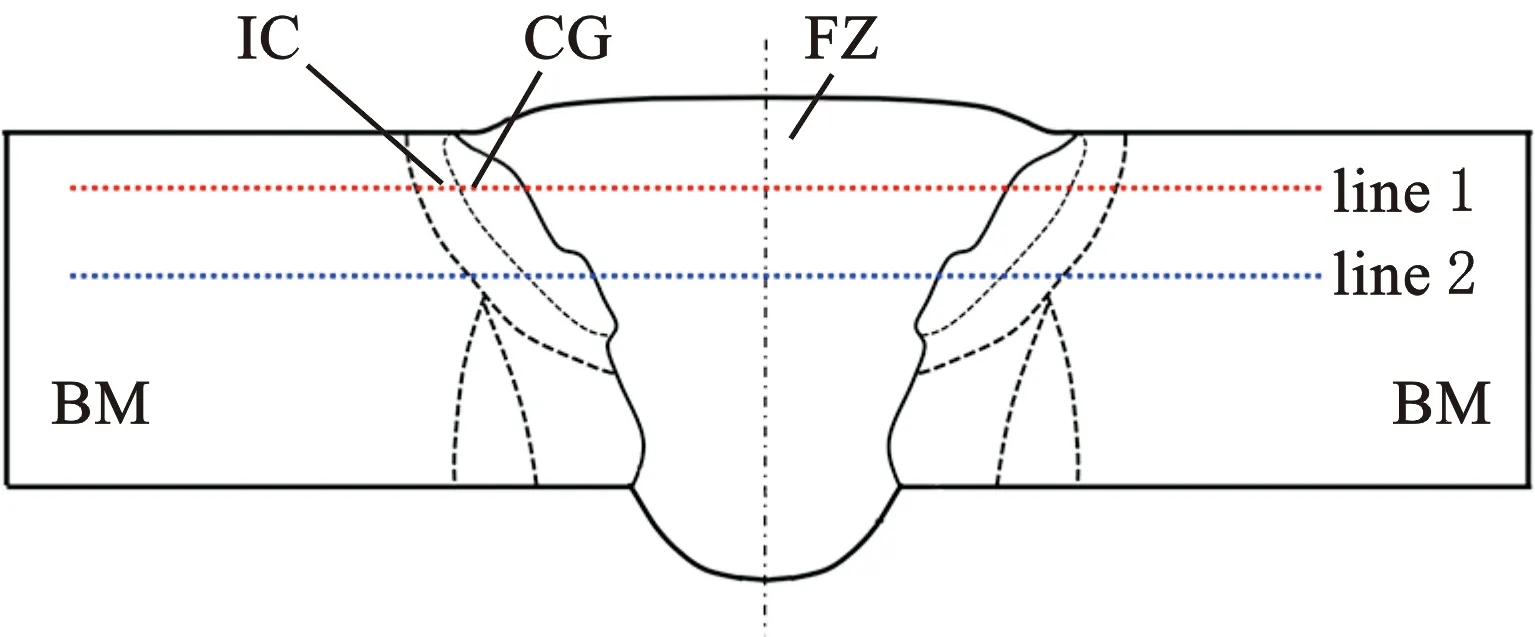
图5 硬度测试路径示意图

2 有限元计算方法

基于SYSWELD软件平台,本研究建立了与实际焊接接头尺寸完全一致的三维有限元模型。在网格划分时,为了平衡计算精度与计算效率,焊缝及其附近的区域网格划分得相对细密,远离焊缝的区域网格划分得相对稀疏,有限元网格模型如图6所示。图6a所示为整体模型的网格分布,所有单元均为8节点6面体单元,单元总数为120 848,节点总数为133 952。图6b所示为横截面上焊缝、热影响区及附近母材区域的网格布置。在模拟多层多道焊接过程时,焊道填充采用“静态单元”的方式进行激活,即未焊接时,使该位置材料的各物理属性接近于0(具体操作为将正常材料属性值乘以一个很小的值,该值为静态单元特性比例系数,本研究设定为0.0001),热源模型加载至该位置时,所对应单元的材料属性恢复正常。

2.1 温度场计算

在焊接过程中,当电弧热进入焊接工件后,热量由高温部分以热传导方式向低温部分扩散。在进行焊接温度场计算时,工件内部的热传导遵循如下控制方程:

(1)

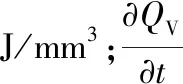
在给定温度值时,cp、λ和ρ由材料的化学成分决定。本研究根据表1中的化学成分,采用JMatPro软件计算得到了Q960E随温度变化的cp(T)、λ(θ)和ρ(θ)数据,整理后如图7所示。计算温度场时,采用了图7所示的热物理性能参数。对于焊缝金属,由于它与母材的化学成分差别并不显著,因此也采用了与母材相同的热物理性能参数。

图7 Q960E热物理性能参数

在焊接过程中,工件与外部环境的热交换为对流和热辐射两种方式。在焊接热过程计算时,采用Newton对流定律[14]考虑对流热交换,采用Stefan-Boltzmann定律考虑热辐射[14],对流散热和辐射散热可分别描述为

(2)

(3)

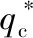
本研究采用Goldak双椭球移动热源模型[17]来模拟焊接电弧的热输入。在该模型中,前半部分和后半部分的热流密度(qf和qr)的分布分别定义为[17]

(4)

(5)

Q=ηUI

式中,Q为电弧功率,W;η为电弧热效率;U为电弧电压,V;I为焊接电流,A;af、ar、b、c为椭球形状参数;ff、fr分别为前后椭球热量分配系数,且ff+fr=2,在本研究中,取ff=0.6,fr=1.4。

2.2 固态相变模型

在焊接的热作用下,温度达到奥氏体相变起始温度θAc1后母材从体心立方(body-centered cubic,BCC)的铁素体开始向面心立方(face-centered cubic,FCC)的奥氏体进行转变。当Q960E母材温度超过奥氏体完全转变温度θAc3后,BCC的铁素体将全部转化为FCC的奥氏体。奥氏体、铁素体、珠光体和贝氏体相变都属于扩散性相变,通常采用经典的Johnson-Mehl-Avrami-Kolmogorov(JMAK)固态相变动力学方程进行描述,由于JMAK方程中JMAK指数n和常数k难以获取,故本研究将对JMAK方程进行简化。

图8所示为Q960E在加热和冷却时所产生热应变与温度之间的关系,该结果是由直径为6 mm、长度为25 mm的Q960E钢试棒采用DIL402C线膨胀仪在加热和冷却速率为15 ℃/min条件下获得的实验结果。由图8可以看出,在θAc1→θAc3温度段,温度与应变间近似于线性关系,因此奥氏体化过程采用线性插值法进行简化处理,即

图8 加热和冷却过程中Q960E热应变与温度的关系图

(6)

根据Q960E钢的过冷奥氏体连续冷却转变曲线(CCT)图[18],当奥氏体从900 ℃冷却至500 ℃的时间小于110 s时,奥氏体相都将转变为马氏体。一般来说,在不采用电渣焊或埋弧焊等方法,或者不采用特别大线能量的气体保护焊进行焊接时,t8/5(即材料从800 ℃冷却至500 ℃所需时间)很难大于110 s。因此,本研究详细考虑了马氏体转变,同时对贝氏体和铁素体转变也进行了简化处理,即将这两种组织都默认为铁素体。铁素体转变为扩散型相变,可用JMAK方程[19]描述该相变转化过程:

(7)

(8)

式(8)中的k和n难以获得,因此需要避开k和n。焊接后冷却是一个连续冷却的过程,扩散型固态相变的转变速率不仅与温度有关,也与冷却速率有关,因此,简化式(8)等号右侧部分为[20]

(9)

完成扩散型相变后,剩余的奥氏体向体心正方(body-centered tetragonal,BCT)的马氏体转变。在马氏体固态相变时,在马氏体相变起始温度θMs开始进行马氏体转变,该过程采用Koisten-Marburger(K-M)方程进行描述[21]：

ξM=1-exp(bM(θMs-θ))

(10)

式中,ξM为马氏体体积分数;θ为当前温度(θ≤θMs);bM为马氏体转变系数,低合金钢的bM值为0.011[22]。

由图8可以得到Q960E的θMs为450 ℃,马氏体完全转变温度θMf为365 ℃。

2.3 应力场计算

在本研究中,温度场、相场(组织场)、应力场与变形采用了“温度-组织-应力”多场耦合的方式来进行计算。金属材料在焊接过程中“热-冶金-力学”的耦合行为非常复杂,材料的总应变包括热应变、弹性应变、塑性应变、相变应变和蠕变应变等多种分量。由于焊接过程中加热和冷却速率都较快,这样在高温停留的累积时间相对较短,因此蠕变应变的影响几乎可以忽略不计[23]。忽略蠕变应变分量后,Q960E钢在焊接过程中的总应变增量Δεij可以由下式得到:

(11)

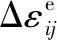
对于Q960E钢,其弹性行为采用各向同性Hooke定律来考虑,塑性行为采用von Mises屈服准则[24]来描述,在本研究中忽略材料的加工硬化效应而采用理想弹塑性模型。对于热应变,采用图8所示的随温度和相体积分数(组织)变化的线膨胀关系进行考虑。对于相变塑性应变的变化,本研究采用Leblond模型[25]来考虑,其表达式如下:

(12)

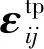
现有研究结果[26]表明,在材料力学性能中屈服强度对焊接残余应力的影响最为显著,因此,本文测量了Q960E钢在常温(25 ℃)、200 ℃、400 ℃、600 ℃和800 ℃条件下的屈服强度。除常温外,其他温度下进行拉伸试验时均未添加引伸计,拉伸试验所得到的不同温度下的应力-应变曲线见图9a。高于800 ℃以上的屈服强度以及其他力学性能参数采用JMatPro软件计算得到。常温到材料熔点范围的力学性能如图9b所示。为了优化有限元计算过程的收敛性,同时保证尽可能小地影响计算精度,当温度高于1200 ℃后,假定材料的屈服强度与弹性模量不会随温度的升高而降低。

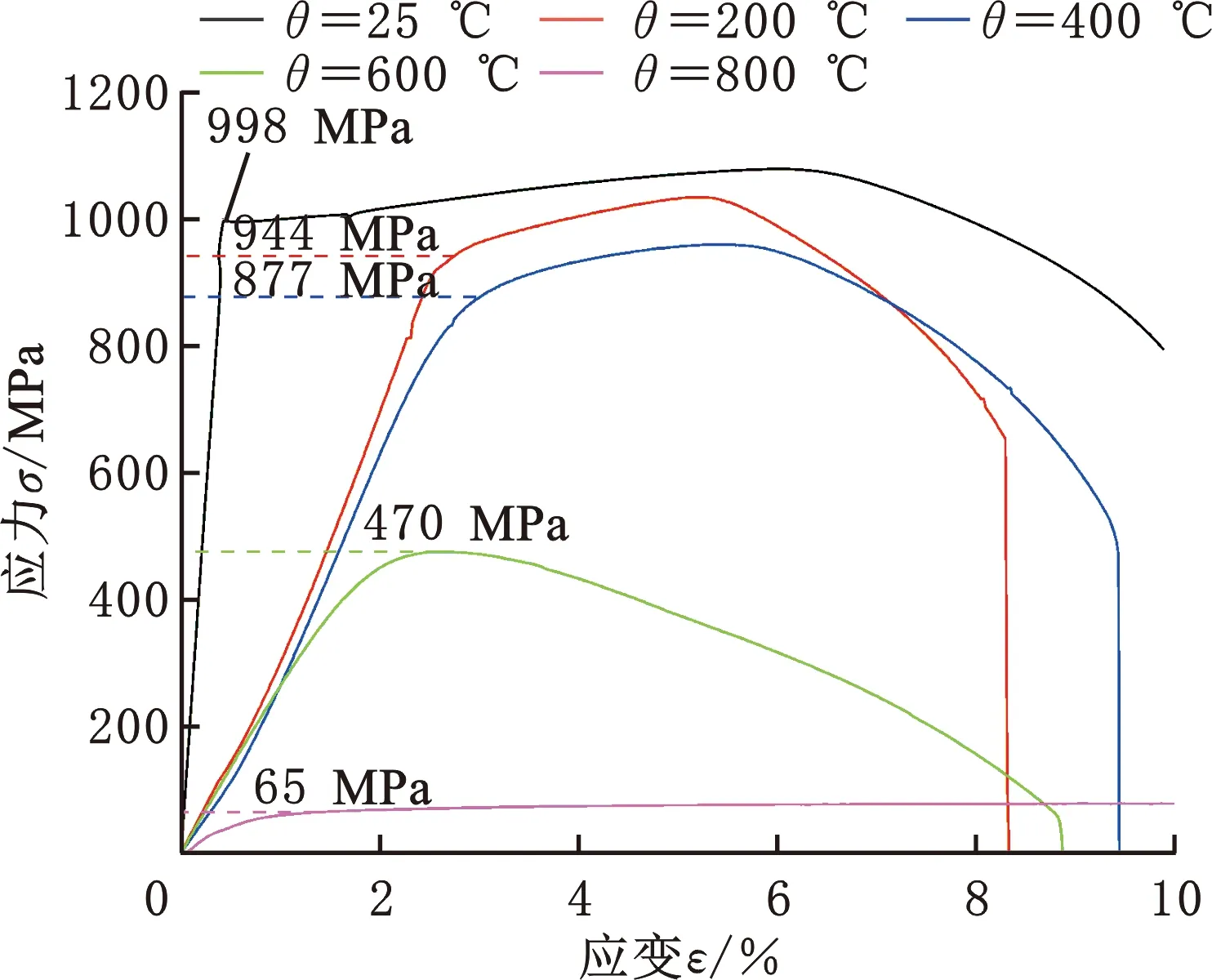
(a)高温拉伸试验

3 结果与分析

3.1 温度场结果

采用Goldak双椭球移动热源模型计算得到的最后一道盖面焊接时的温度场如图10a所示,焊接接头中央截面的温度分布如图10b所示,图中灰色部分为峰值温度超过冶金熔点的区域,而红色至黄绿色区域为热影响区。总体上,数值模拟结果与实际焊接接头的焊缝区域及热影响区吻合较好。

(b)焊道峰值温度

为了定量比较数值模拟和实验测量的焊接温度循环曲线,在有限元模型中选取了与图2中A、B和C位置完全对应的三个节点来输出热循环曲线。数值模拟得到三个点的热循环曲线与对应的实验结果如图11所示,可以看出,尽管计算值与实验值在局部有些差异,但整体而言,不论是各点的峰值温度还是升温速率和降温过程,数值模拟结果都与实验结果吻合较好。

图11 焊接温度循环的模拟结果与实验结果的比较

3.2 热影响区组织的体积分数模拟结果

图12所示为Q960E钢多层多道对接接头中热影响区(指粗晶区和细晶区,下同)的焊态马氏体体积分数分布,可以看到,热影响区的焊态马氏体体积分数超过了90%。

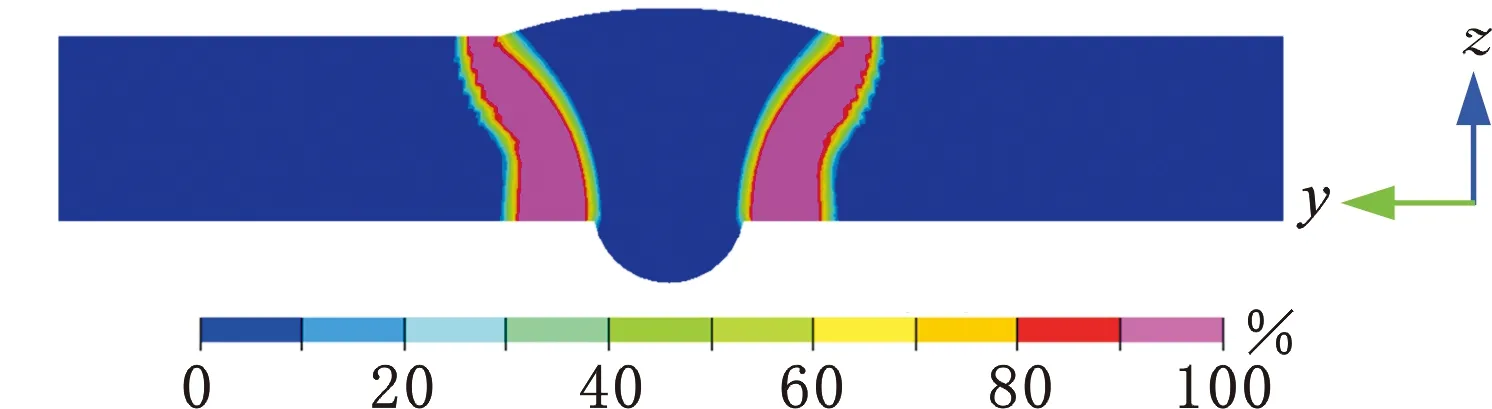
图12 计算得到的马氏体分布云图

图13为Q960E钢对接接头的金相组织图,其中图13a为焊接接头宏观照片,图13b、图13c、图13d所示分别为FZ、CG和IC的金相组织。从图13中可以看到,焊接热影响区中粗晶区的组织几乎全部为粗大的马氏体,模拟得到的马氏体体积分数超过90%,与实验结果比较吻合。如图13b所示,在实际焊接接头中焊缝组织以针状铁素体为主,而在本研究的材料模型中并没有考虑焊缝金属的马氏体相变。由于部分相变区非常窄小,故在本研究的材料模型中未考虑部分相变区力学性能的变化。

(a)接头宏观形貌 (b)FZ

图14所示为沿着line 1和line 2的硬度分布。由line 1的硬度分布可知,第四焊道(最后一道)产生的热影响区的硬度值最大,其峰值为375HV,而接头左侧热影响区(由倒数第二焊道产生)的硬度峰值与母材平均硬度相当,这可能是由于该热影响区的马氏体受到最后一道焊接过程的回火作用而使硬度有一定幅度降低。此外,从图中可以很明显地看到,在部分相变区及其附近的硬度显著降低,说明Q960E焊接接头存在软化区。line 2的硬度分布趋势与line 1非常相似。

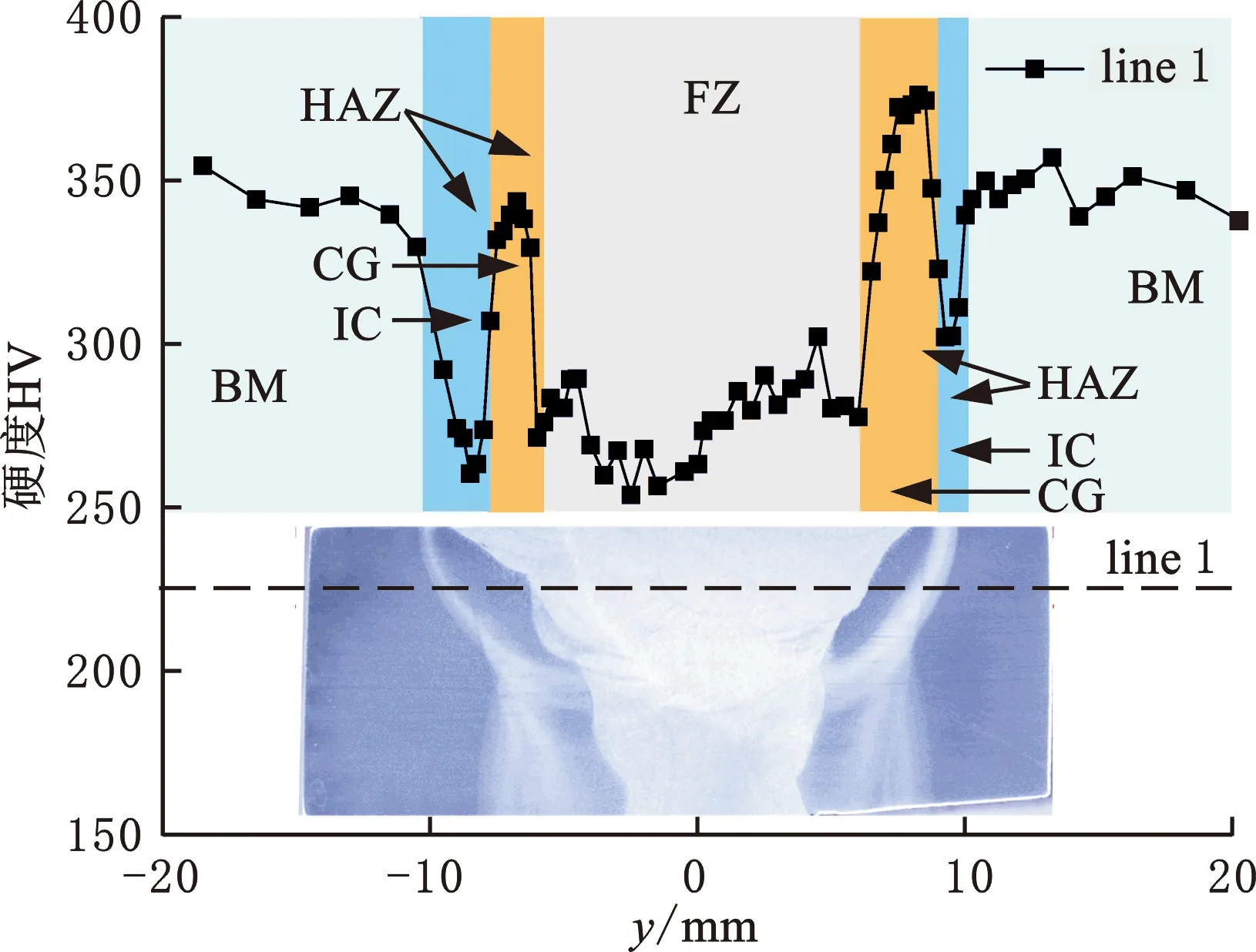
(a)line 1硬度分布

金相组织和硬度测量结果证明了热影响区(尤其是粗晶区)产生了马氏体相变,因此,本研究中开发的材料模型重点考虑了固态相变。由于接头存在软化区以及在多层多道焊条件下的回火效应,在后续的研究中,除了考虑固态相变外,在材料模型中考虑软化及回火效应也是有必要的。

3.3 焊接残余应力

3.3.1纵向残余应力

数值模拟得到的Q960E多层多道对接接头的纵向残余应力分布如图15所示,其中,图15a为接头整体的纵向残余应力分布云图,图15b为中央截面上焊缝及其附近区域的纵向残余应力分布云图。从图15中可以看出,在焊缝区与紧邻热影响区的母材上产生了很大的纵向拉伸残余应力,峰值应力略大于母材常温屈服极限。而在焊缝两侧热影响区上,纵向残余应力值较小,这是因为马氏体相变对该区域残余应力的大小和分布产生了抑制作用。这里需要说明的是,由于最后的盖面焊道热输入相对较大,加上试板厚度仅为10 mm,故最后一道焊接产生的热影响区范围相对较大。此外,盖面焊接采用了左右两道分别焊接的方式来完成,因此在中央截面上的纵向残余应力呈现出不对称分布特征。

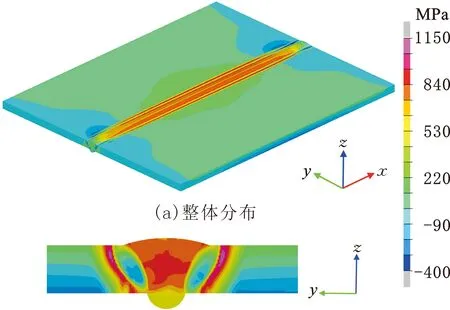
(b)中央截面分布

图16所示为Q960E钢对接接头中央截面上表面纵向残余应力分布的数值模拟结果与实验测量结果的对比。从图中可知,在y=-10.8 mm位置处的纵向残余应力值最大,达到了988 MPa。Q960E 钢对接接头的纵向拉伸残余应力峰值位于紧邻热影响区细晶区的母材上,这一点与强度级别较低的低合金高强钢(如Q345钢)不一样。后者的固态相变虽然对残余应力的演化过程有影响,但接头的纵向拉伸残余应力峰值往往存在于热影响区中。图中y=-10.8～-9.2 mm与y=9.2～10.9 mm之间的区域对应于接头热影响区,该区域内的纵向残余应力有显著的减小。焊缝两侧热影响区内的纵向残余应力最小值约为400 MPa,明显低于材料常温屈服极限,表明固态相变会减小该区域的残余应力。与P91钢[27]、P92[28]钢及低温相变(LTT)焊材焊接接头[29]的残余应力相比,Q960E钢焊接接头热影响区的纵向残余应力并没有发生质的变化(即变为压缩残余应力)。这是因为Q960E钢中马氏体的相变开始温度较高,材料自身的屈服强度也明显高于前几种材料的屈服强度。同时,从图16中还可以看出,虽然焊缝的纵向残余应力峰值小于紧邻热影响区的应力值,但焊缝处的纵向残余应力也达到了熔覆金属的屈服强度。这里需要说明的是,在测量焊缝的残余应力时,需要对焊缝金属进行适当打磨使其平整以利于测量,而机械打磨过程中不可避免地要引入塑性变形,因此焊缝金属表面纵向残余应力测量值与数值模拟结果存在一定程度的差异。但总体而言,接头残余应力的数值模拟结果与实验测量结果在分布形态和峰值大小上均吻合较好。

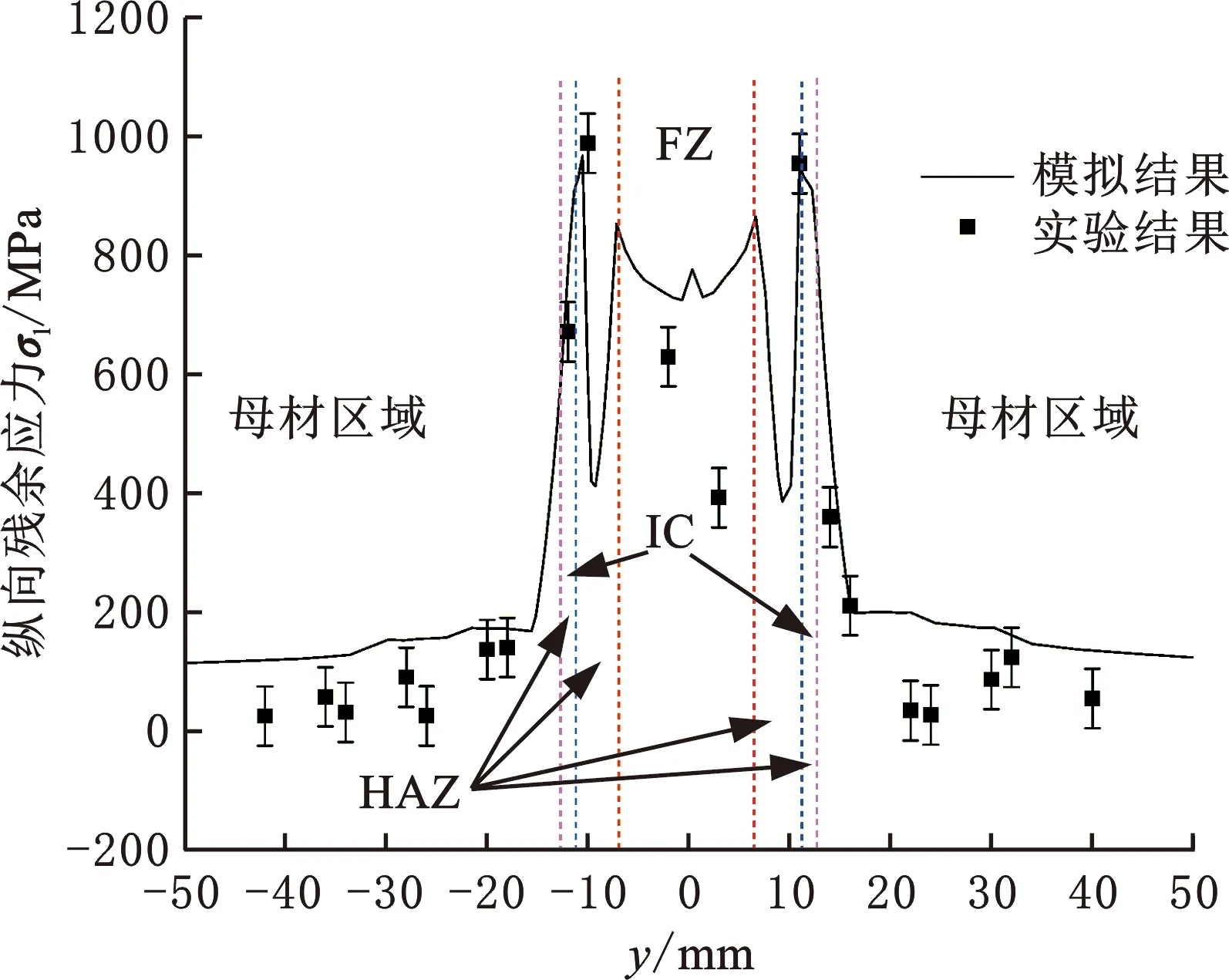
图16 Q960E纵向残余应力的实验值与模拟值

图17所示为Q960E钢对接接头在多层多道(三层四道)焊接过程中纵向残余应力演化过程,其中图17a～图17d所示分别为第1～4焊道焊接完成并冷却到层间温度或室温时的纵向残余应力分布。在第一道焊完成后,焊缝金属及紧邻热影响区的母材上均产生了较高的拉伸残余应力,而且呈现对称分布。在焊缝的材料模型中没有考虑固态相变,焊缝金属的纵向残余应力基本与熔覆金属的屈服强度相当;而在热影响区的材料模型中考虑了马氏体相变,由马氏体相变引起的体积膨胀抵消了相变前的累积拉伸应力,因而冷却到层间温度时,热影响区的纵向应力值较小。在二道焊完成后,同样产生了对称分布的纵向残余应力,但是第一道焊冷却到层间温度的应力分布明显地被第二道焊改变了。由表2可知,第二道焊的热输入要明显大于第一道焊的热输入,因而第二道焊产生的热影响区更大,但纵向残余应力的分布形态与第一道焊相似。第三道焊完成后,产生了左右明显不对称的应力分布。由于第三道焊的热输入相对较小,它在母材上产生的热影响区只在左侧存在。第四道焊完成后,由于第四道焊的热输入较大,在右侧母材上产生了较大的热影响区,最终纵向残余应力分布的形态趋于对称。

(a)第一焊道 (b)第二焊道

3.3.2横向残余应力

Q960E钢对接接头的横向残余应力分布云图见图18,其中图18a所示为接头整体的横向残余应力分布,图18b所示为中央截面的横向残余应力分布。整体来看,横向残余应力的拉应力区域主要在焊趾位置,最大值接近600 MPa,而热影响区内部的横向残余应力相对较小,甚至出现了压应力。

(b)中央截面分布

图19所示为Q960E钢对接接头中央截面上表面的横向残余应力数值模拟结果与实验结果的对比。数值模拟结果的分布形态与实验测量结果基本一致,但实验测量得到的横向峰值应力要明显小于数值模拟结果。实验测量出的最大值为337 MPa,相同位置处计算得到的峰值为456 MPa;在热影响区边缘实验中测量得到的最小值为-159 MPa,相同位置处计算得到的最小值为-147 MPa。由图19可知,尽管数值模拟结果与实验结果尤其是峰值应力存在一定差异,但两者的分布形态基本一致,总体上吻合较好。

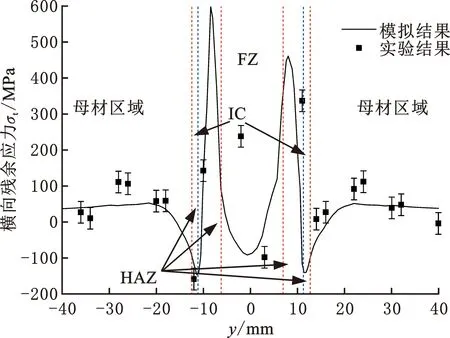
图19 Q960E横向残余应力实验值与模拟值

3.4 焊接变形结果

数值模拟得到的对接接头的x、y、z方向及合成位移分布云图见图20。从图20a中可以看出,在焊缝及其附近区域的两个端部,x方向(纵向)位移的绝对值较大,远离焊缝位置的纵向位移量逐渐减小,而且整个接头的纵向收缩极不均匀,其中焊缝位置的最大收缩量约为1.2 mm。图20b为对接接头在y方向(横向)的位移分布云图,由此图可知,试板中央位置横向收缩较大,而两个端部的横向收缩较小,上表面的最大横向收缩量约为2.3 mm。图20c为z方向位移(即面外变形)的分布云图,由此图可知,z向位移的最大差值(最大值与最小值之差)约为7 mm。对接接头产生了一定程度的纵向弯曲变形,焊缝两端的z向位移为-1 mm,焊缝中央位置的z向位移为2 mm。除了纵向弯曲外,试板两侧因角变形也产生较大的z向位移,右侧板边缘的最大z向位移约为6 mm。图20d所示为焊接试板的合成位移,此图与图20c分布相似,这说明采用V形坡口的Q960E钢焊接接头的主要变形贡献来自面外变形(即角变形和纵向弯曲)。

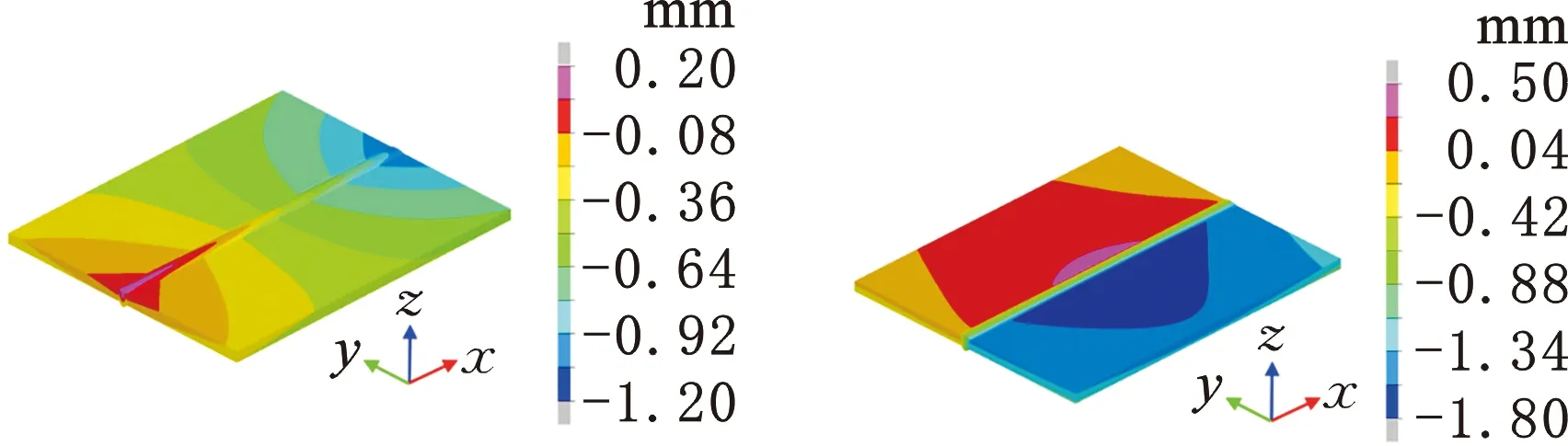
(a)x方向位移云图 (b)y方向位移云图

图21a比较了由数值模拟和实验测量得到的试板上表面的横向收缩分布。在x=90 mm位置,数值模拟得到的横向收缩为-1.80 mm,而实测值为-1.68 mm(负号表示收缩,下同);在x=180 mm位置,数值模拟值为-1.99 mm,而实测值为-1.85 mm;在x=270 mm位置,数值模拟值为-1.82 mm,而实测值为-1.62 mm。总体而言,数值模拟得到的横向收缩值略大于实验值,但两者的相对误差小于15%。图21b比较了由数值模拟和实验测量得到的中央截面上的角变形,由图可以看出,实验值与计算值的吻合度超过了95%。由上述结果可知,本研究开发的数值模拟方法能较高精度地模拟Q960E钢多层多道对接接头的焊接变形。

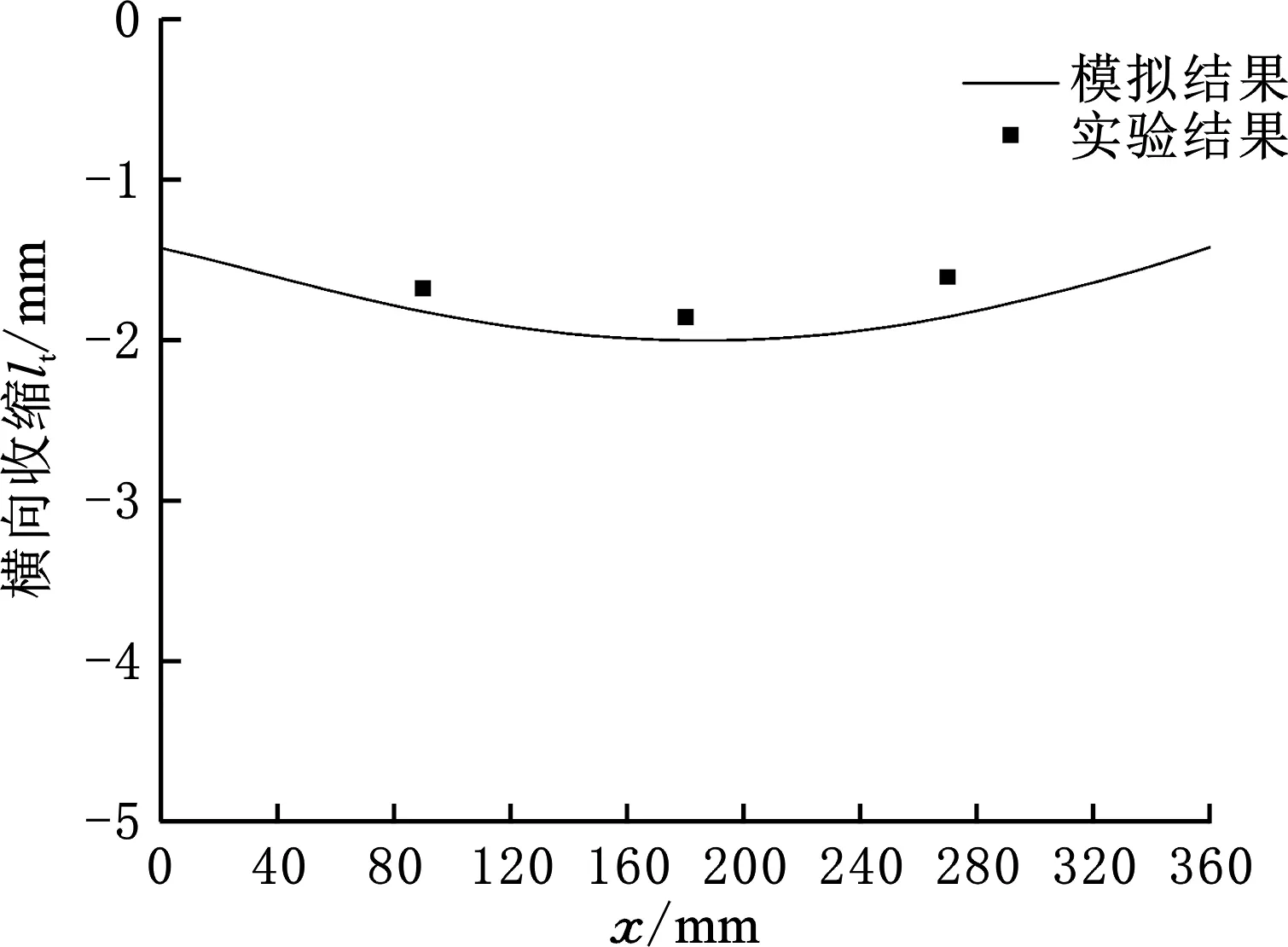
(a)横向收缩

4 结论

(1)以Q960E钢多层多道对接接头为研究的对象,基于SYSWELD软件平台开发了“热-组织-应力”多物理场耦合的弹-塑性有限元计算方法,采用该方法计算了对接接头的温度场、热影响区的组织体积分数、残余应力与焊接变形。比较数值模拟结果和实验结果可知,无论是焊接温度循环与组织体积分数,还是残余应力与焊接变形,两种结果均吻合良好,验证了本工作所开发的数值模拟方法的有效性。

(2)数值模拟结果表明,因Q960E钢淬透性高,热影响区易发生马氏体相变,这将导致对接接头热影响区粗晶区位置的焊接残余应力显著减小,而峰值应力将出现在热影响区边缘紧邻母材的位置。

(3)从数值模拟结果来看,在对接接头的焊趾位置处出现了较大的拉伸横向残余应力,焊趾处的最大横向残余应力值为600 MPa。

(4)Q960E钢的多层多道对接接头中存在明显的软化区域,同时后焊焊道对先焊焊道热影响区(有组织转变的区域)有一定程度的回火效应。因此,为了更高精度地模拟焊接残余应力,有必要在后续研究中建立材料的软化模型和回火模型。